基于云模型人工魚群算法的模糊優(yōu)化設計

高 翔，王林軍，杜義賢，李 響，徐 柳

（1.三峽大學水電機械設備設計與維護湖北省重點實驗室，湖北宜昌443002；2.三峽大學機械與動力學院，湖北宜昌443002）

針對機械結構的模糊優(yōu)化設計［1-3］，許多學者都開展了相關研究，并取得了大量成果。例如：Qiu等［4］利用SVR（support vector regression，支持向量回歸）算法構造了等效極限狀態(tài)方程，并采用解耦算法求解了同時包含區(qū)間變量和模糊變量的可靠性優(yōu)化設計問題；Huang等［5］通過度量函數(shù)來自動設置目標函數(shù)的權重，并對簡支工字梁和齒輪箱進行了模糊多目標優(yōu)化設計；Li 等［6］改進了NSGA-II（non-dominated sorting genetic algorithm-II，非支配排序遺傳算法-II）算法，并對旋轉導向鉆井系統(tǒng)進行了多目標模糊優(yōu)化；王德浩［7］通過APDL（ANSYS parametric design language，ANSYS 參數(shù)化設計語言）調(diào)用ANSYS DesignXplorer 內(nèi)置的MOGA（multi-objective genet‐ic algorithm，多目標遺傳算法），對大載重集裝箱進行了多目標模糊優(yōu)化設計；李召等［8］基于混沌理論對布谷鳥算法進行了改進，并對永磁聯(lián)軸器進行了模糊多目標優(yōu)化設計；熊勇［9］提出了一種單目標函數(shù)權重的更新方法，將多目標優(yōu)化問題轉化為單目標優(yōu)化問題，并基于遺傳算法求解了兩級行星汽車輪邊減速系統(tǒng)的模糊多目標優(yōu)化設計問題。

但是，文獻［6-9］中所用優(yōu)化算法的全局尋優(yōu)能力較差，而李德毅等［10］提出的云模型中的正向云發(fā)生器可顯著提高上述優(yōu)化算法的全局尋優(yōu)能力和收斂速度。對于人工魚群算法的改進，宋曉［11］將以當前解作為云模型期望時產(chǎn)生新解的過程稱為云變異，將以2 個當前解的加權平均和作為云模型期望時產(chǎn)生新解的過程稱為云學習，并將云變異因子和云學習因子引入人工魚群算法；王明永［12］通過隸屬度與遞減數(shù)列來選擇隨機行為和云模型正向云發(fā)生器的執(zhí)行，使得人工魚群算法前期通過隨機行為進行全局搜索，后期通過云模型正向云發(fā)生器進行局部搜索。

鑒于云模型已廣泛應用于優(yōu)化算法的改進，筆者利用云模型中的正向云發(fā)生器對人工魚群算法進行改進（稱為云模型人工魚群算法）；將當前最優(yōu)解作為云模型的期望，以提高收斂速度，并同時采用隨機行為和正向云發(fā)生器，以結合2 種方法的優(yōu)勢。然后，結合增廣乘子法和云模型人工魚群算法，對直齒圓柱齒輪和內(nèi)燃機氣門彈簧的模糊優(yōu)化問題進行求解。該優(yōu)化方法的優(yōu)勢在于：1）常用的罰函數(shù)法的收斂性依賴于罰因子的初始值，而本文采用的增廣乘子法的收斂性不依賴于罰因子的初始值；2）直接調(diào)用MATLAB軟件中內(nèi)置的距離函數(shù)pdist2來計算人工魚之間的距離，簡化了原人工魚群算法的代碼；3）采用模糊綜合評判來確定相關參數(shù)的最優(yōu)水平截集，可實現(xiàn)機械零部件的模糊優(yōu)化設計。

1 增廣乘子法

為了更方便地求解具有約束的優(yōu)化模型，提出了罰函數(shù)法，其被廣泛應用于優(yōu)化問題的求解。但是，當罰因子取值不合適時，罰函數(shù)法不收斂。為此，采用增廣乘子法對外罰函數(shù)法進行改進［13］。

對于具有L個不等式約束的數(shù)學模型，可將其表示為：

其中：x為設計變量；f(x)為目標函數(shù)；gk(x)為第k個約束條件；Rv為v個設計變量對應的實數(shù)域。

引入松弛變量y，將不等式約束條件轉化為等式約束條件，則上述數(shù)學模型可轉化為：

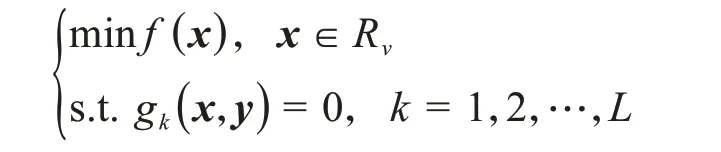
基于上述數(shù)學模型，構造增廣乘子函數(shù)［13］：

式中：ζk為第k個約束條件對應的拉格朗日乘子；η為罰因子。

當?Mζ(x，y，ζ，η) =0 時，增廣乘子函數(shù)取得極值，即當時，有：

則上述數(shù)學模型可轉化為：

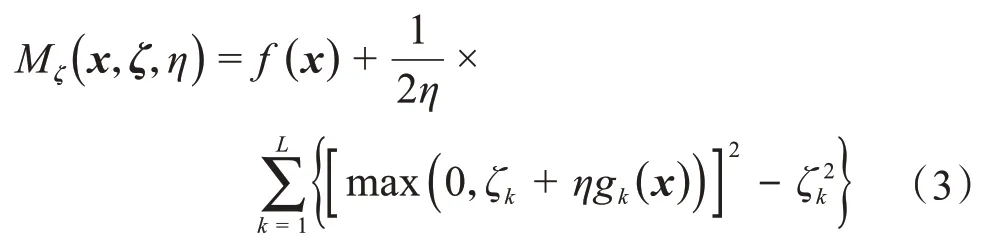
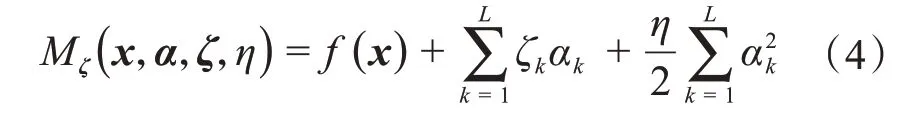
2 云模型人工魚群算法

2002年，李曉磊等［14］提出了一種模仿魚群追尾、群聚和覓食等行為的人工魚群算法，該算法可用于尋找函數(shù)的最優(yōu)值［15-16］。

2.1 群聚行為

設人工魚i與人工魚j之間的距離為dij，若dij小于當前視野Vi，則人工魚j在人工魚i的視野范圍內(nèi)。假設當前人工魚i的視野Vi內(nèi)有nf條人工魚，且視野內(nèi)所有人工魚所在位置的平均值為Pmean，對應的適應度為Fmean。若當前人工魚i的適應度Fi滿足，則群聚行為后，人工魚i所在的位置Pi，swarm為：式中：Pi為人工魚i的當前位置；prand為[0，1]內(nèi)的隨機數(shù)；Si為人工魚i的當前步長。

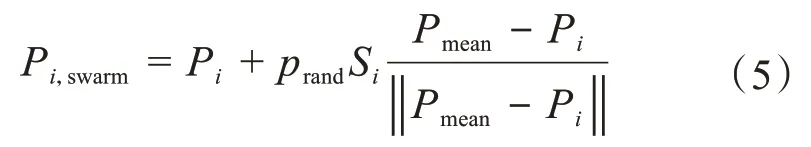
若位置Pi，swarm對應的適應度Fi，swarm小于當前的適應度Fi，則更新人工魚i的位置和適應度。

2.2 追尾行為

?人工魚i的適應度Fi滿足，則追尾行為

當前人工魚i視野內(nèi)有nf條人工魚，且視野內(nèi)最佳個體的位置為Pmin，對應的適應度為Fmin。若當前后，人工魚i所在的位置Pi，follow為：

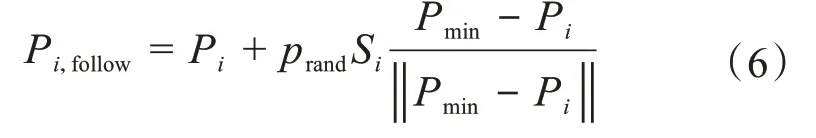
若位置Pi，follow對應的適應度Fi，follow小于當前的適應度Fi，則更新人工魚i的位置和適應度。

2.3 覓食行為

在覓食行為初期，向視野Vi內(nèi)任意方向運動一步后，人工魚i所在的位置Pi，prey為：

若位置Pi，prey對應的適應度Fi，prey小于當前的適應度Fi，則更新人工魚i的位置和適應度，更新后Pi，prey為：

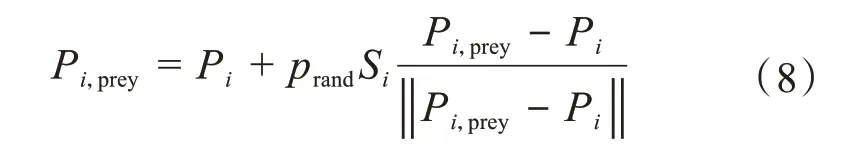
若更新后的適應度Fi，prey仍小于當前的適應度Fi，則不斷更新人工魚的位置和適應度，當覓食次數(shù)達到ntry時，覓食行為終止。

2.4 隨機行為

李德毅等［10］基于模糊集中的隸屬函數(shù)提出的云模型包括正向云發(fā)生器和反向云發(fā)生器。其中正向云發(fā)生器常用于智能優(yōu)化算法的改進。

在云模型中，正向云發(fā)生器［16］生成的新人工魚的位置Pnew的隸屬度Ψ為：

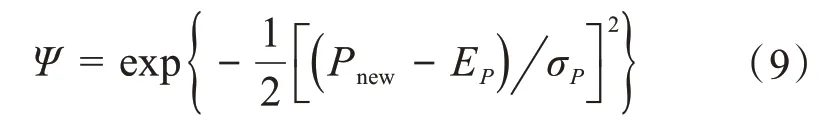
式中：EP為當前新人工魚位置的最優(yōu)解；σP為新人工魚位置的標準差，其中En、He分別為熵和超熵［17］，En=為新人工魚位置的取值范圍，n為當前迭代次數(shù)，nmax為迭代次數(shù)上限。

若隸屬度Ψ大于隨機數(shù)，則Pnew為新人工魚的位置；否則新人工魚為隨機個體。

2.5 繁殖行為

若Pbest為全局最優(yōu)解，則繁殖行為后，人工魚i所在的位置Pi，reproduct為［16］：

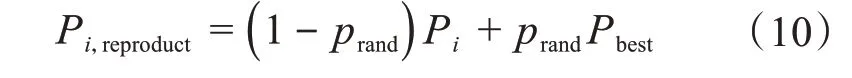
2.6 公告板

文獻［15］中并未給出公告板的計算方法，本文擬自行構造相關公式，并將其引入人工魚群算法。

若人工魚i的當前適應度Fi小于上次迭代的適應度Fi，old，則公告板操作后人工魚i所在的位置Pi，bulletin為：

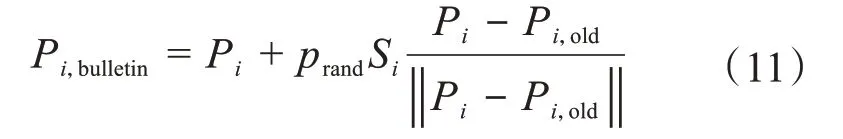
若位置Pi，bulletin對應的適應度Fi，bulletin小于當前的適應度Fi，則不斷更新人工魚的位置和適應度。當公告板的操作次數(shù)達到ntry時，公告板操作終止。

2.7 參數(shù)更新

第n次迭代時，人工魚i的視野Vi，n和步長Si，n的更新公式為［18］：

其中：

式中：ξ1、ξ2為常數(shù)。

綜上，云模型人工魚群算法的步驟為：

1）初始化種群，并計算人工魚的適應度。

2）開始迭代，n=n+1。

3）計算視野和步長的更新參數(shù)γ。

4）記錄當前人工魚的位置及適應度，便于公告板的執(zhí)行。

5）計算當前人工魚和其他人工魚的距離。

6）更新視野和步長。

7）若視野內(nèi)有其他人工魚，且滿足相應的判斷條件時，則依次執(zhí)行群聚行為和追尾行為；否則不執(zhí)行任何行為。

8）執(zhí)行覓食行為，當覓食次數(shù)達到ntry時，終止覓食行為。

9）通過正向云發(fā)生器得到新人工魚的位置Pnew，并計算隸屬度Ψ。若隸屬度Ψ大于隨機數(shù)，則接受新解；若不滿足，則隨機生成新解。

10）執(zhí)行繁殖行為。

11）執(zhí)行公告板操作，當次數(shù)達到ntry時，終止公告板操作。

12）當?shù)螖?shù)達到nmax時，迭代終止，否則轉至步驟2）。

在原人工魚群算法中，群聚行為和追尾行為的子程序內(nèi)分別包含1次覓食行為［15］，即在每次迭代中每個個體可能執(zhí)行2次覓食行為，而云模型人工魚群算法僅在追尾行為和群聚行為結束后單獨執(zhí)行1次覓食行為，以確保在每次迭代中每個個體僅執(zhí)行1次覓食行為。

人工魚群算法［18-22］通常使用自定義程序來計算人工魚之間的距離［15］，導致運算量較大，而本文直接調(diào)用MATLAB軟件中內(nèi)置的距離函數(shù)pdist2來計算人工魚之間的距離，以簡化代碼。

3 直齒圓柱齒輪的模糊優(yōu)化設計

設直齒圓柱齒輪的輸入功率為10 kW，小齒輪的轉速為960 r/min，傳動比u=3.2；小齒輪的材料為40Cr，大齒輪的材料為45鋼。直齒圓柱齒輪的彈性影響系數(shù)ZE=189 MPa1/2，載荷系數(shù)KH=1.91，重合度系數(shù)Zε由小齒輪齒數(shù)和傳動比確定。考慮到直齒圓柱齒輪的變位系數(shù)為0，則區(qū)域系數(shù)ZH=2.5。以直齒圓柱齒輪體積最小［13，23］為優(yōu)化目標，建立如下數(shù)學模型：

式中：m為直齒圓柱齒輪的模數(shù)；z1為小齒輪齒數(shù)；?為齒寬系數(shù)；σH為直齒圓柱齒輪的接觸疲勞應力；[σH]為許用接觸疲勞應力；σF1、σF2分別為小齒輪、大齒輪的彎曲疲勞應力；[σF1]、[σF2]分別為小齒輪和大齒輪的許用彎曲疲勞應力；T1為直齒圓柱齒輪輸入軸的扭矩；YFa1、YFa2分別為小齒輪、大齒輪的齒形系數(shù)；YSa1、YSa2分別為小齒輪、大齒輪的的應力修正系數(shù)；變量中上橫線表示相應參數(shù)的上限，下橫線表示下限，下文同。

通常情況下，直齒圓柱齒輪的模數(shù)m=2～10；當齒輪為閉式齒輪時，小齒輪齒數(shù)zl=20～40；當小齒輪采用不對稱布置時，齒寬系數(shù)?=0.7～1.15。由文獻［25］可知，小齒輪和大齒輪的許用接觸疲勞應力分別為540 和523 MPa，許用彎曲疲勞應力分別為303.57 和238.86 MPa。為便于計算，本文取。

對于齒輪許用應力，通常取擴增系數(shù)β=1.01，由擴增系數(shù)法得。

為了方便計算，所有約束條件的隸屬函數(shù)均取線性隸屬函數(shù)。基于最優(yōu)水平截集法，上述約束條件可轉化為：

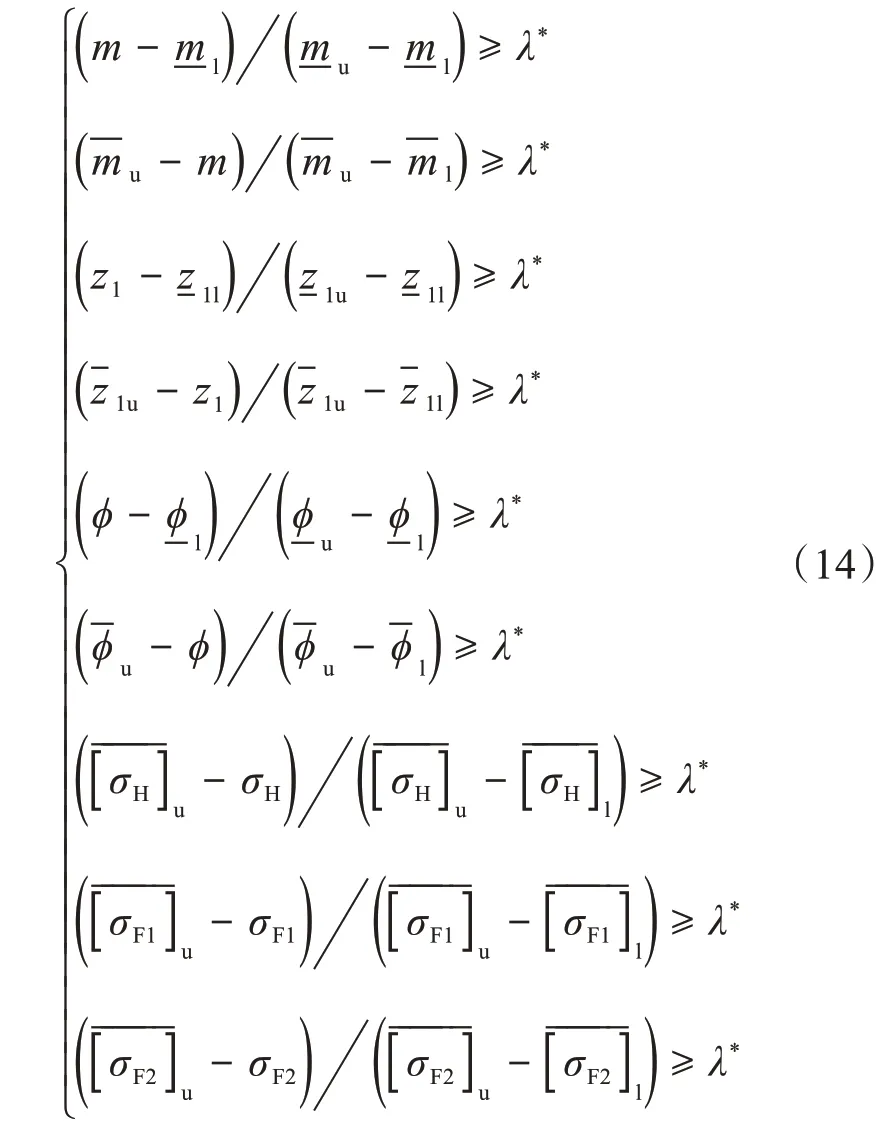
式中：λ*為最優(yōu)水平截集對應的參數(shù)，λ*∈(0，1)。

對于因素權重矩陣A，其計算方法有2 種：專家調(diào)查法和專家評議法［2］。前者是根據(jù)多位專家給出的因素權重矩陣，直接通過計算平均值得到；后者是根據(jù)多位專家給出的因素重要性序列，通過計算得到優(yōu)先得分表，并根據(jù)得分表計算因素權重矩陣。在本文中，基于專家調(diào)查法計算得到的因素權重矩陣A=［0.25 0.25 0.15 0.10 0.10 0.15］。

直齒圓柱齒輪性能的影響因素及其等級如表1所示。若希望某個因素達到某個設計等級，則對應的隸屬度應稍大。假設要得到一個設計水平、制造水平和材料質(zhì)量較高，使用條件、維護費用和重要程度一般的設計方案，則對應的隸屬度取值如表2所示。

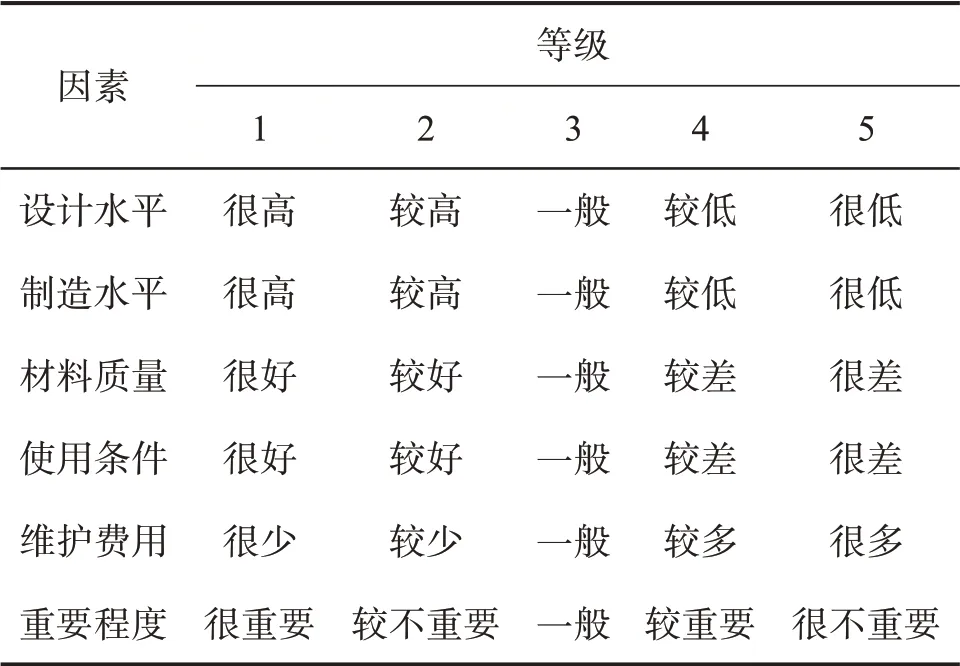
表1 直齒圓柱齒輪性能的影響因素及其等級Table 1 Performance influencing factors and their grades for spur gear

表2 直齒圓柱齒輪的單因素評判隸屬度Table 2 Single factor evaluation membership degree of spur gear

對通過單因素評判得到的直齒圓柱齒輪性能等級隸屬度矩陣μ進行歸一化處理，得到第h個因素的等級權重矩陣Wh。

為了確定最優(yōu)水平截集對應的參數(shù)λ*，假設備擇集λ=［0.10 0.30 0.45 0.50 0.55 0.70 0.85 1.00］。若備擇集元素個數(shù)與因素等級個數(shù)相等，則等級評判矩陣主對角線的元素均為1。在本文中，由于備擇集的元素個數(shù)與因素等級個數(shù)不相等，則假設所有因素的等級評判矩陣Rh相同，為：

模糊綜合評判的合成運算共有4種：主因素決定型M(∧，∨)、主因素突出型M(∧，⊕)和M(?，∨)以及加權平均型M(?，+)［24］。本文選用加權平均型M(?，+)進行模糊綜合評判的合成運算。

設罰因子η=5，100和1 000時，利用增廣乘子法無法得到滿足約束條件的解。為使所得結果滿足約束條件，須增大罰因子。取罰因子η=10 000，利用增廣乘子法求解時所有約束條件均可滿足。由此可知：較大的罰因子有利于確保約束條件被滿足。

本文采用云模型人工魚群算法、人工魚群算法和人工蜂群算法分別求解直齒圓柱齒輪的模糊優(yōu)化問題，并對其結果進行比較。為減少運算量，通過向量化編程技術對人工蜂群算法［15］進行簡化。此外，人工蜂群算法中的偵查蜂操作可能會使最優(yōu)個體被更新，從而導致最優(yōu)個體被破壞，本文通過添加相關代碼來保護最優(yōu)個體，使得偵查蜂操作不會對拖尾次數(shù)太大的最優(yōu)解進行更新。

取罰因子η=10 000，將拉格朗日乘子從0增大至1×10-6。設人工魚群算法中的覓食次數(shù)為5，擁擠度為0.618；人工魚群算法和人工蜂群算法中的種群數(shù)量均為20，迭代上限均為50 次。基于3 種方法的直齒圓柱齒輪模糊優(yōu)化的迭代過程如圖1所示，優(yōu)化結果如表3所示。

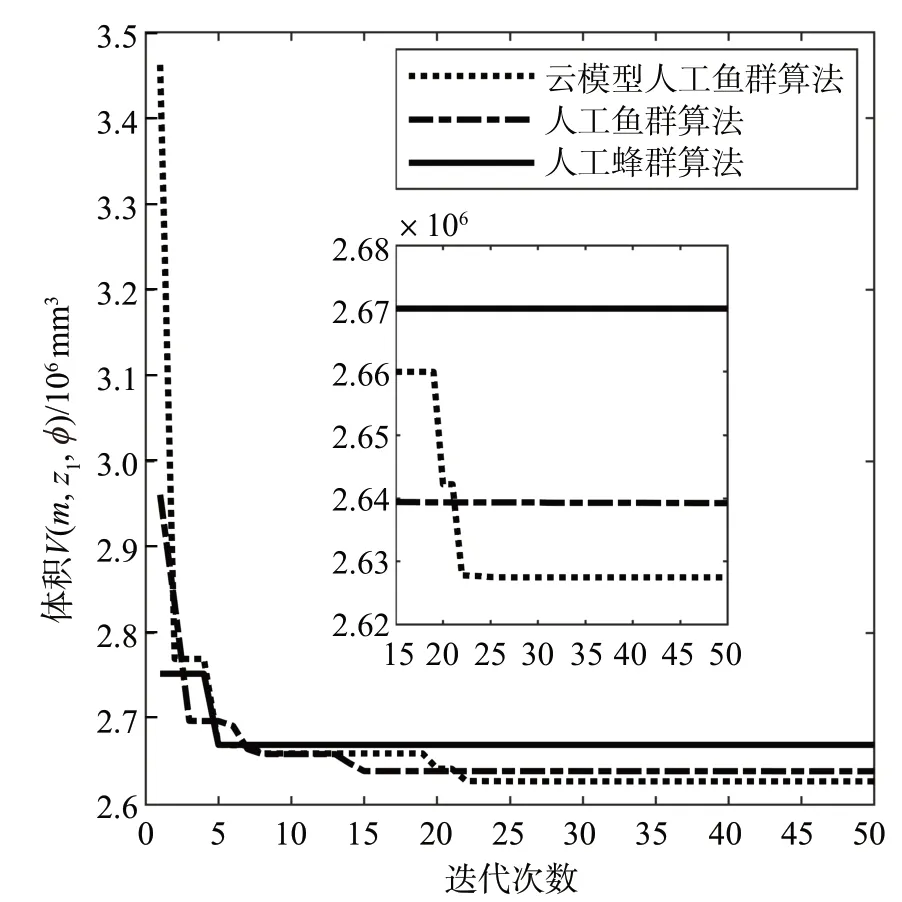
圖1 直齒圓柱齒輪模糊優(yōu)化的迭代過程Fig.1 Iteration process of fuzzy optimization for spur gear

表3 直齒圓柱齒輪模糊優(yōu)化設計結果Table 3 Fuzzy optimization design result of spur gear

由圖1和表3可知：

1）利用人工魚群算法優(yōu)化得到的直齒圓柱齒輪體積為2.627×106mm3，較利用云模型人工魚群算法優(yōu)化得到的體積（2.639×106mm3）大，由此說明云模型可顯著提高人工魚群算法的尋優(yōu)能力。

2）人工蜂群算法的收斂速度較慢，且其優(yōu)化效果比2種人工魚群算法差。

由上述優(yōu)化結果可知：當m=2 mm，利用云模型人工魚群算法求得直齒圓柱齒輪的體積最小時，z1=39.0，?=0.630 0；當m=1.5 mm，利用云模型人工魚群算法求得直齒圓柱齒輪的體積最小時，z1=41.7，?=1.208 0。固定m和z1，采用文獻［25］中用于求解混合離散變量優(yōu)化問題的擬離散法——連續(xù)分量優(yōu)化法進一步優(yōu)化?，并對直齒圓柱齒輪的疲勞強度進行校核，結果如表4所示。

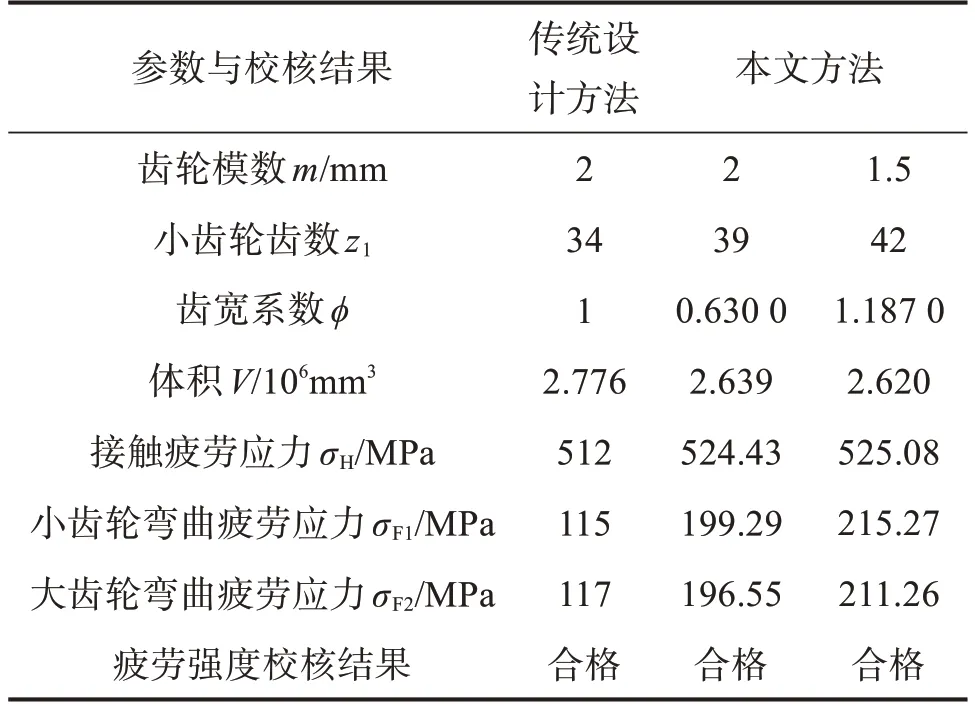
表4 基于不同方法的直齒圓柱齒輪優(yōu)化設計結果對比Table 4 Comparison of optimization design results of spur gear based on different methods

由表4可知，利用傳統(tǒng)設計方法得到的直齒圓柱齒輪體積為2.776×106mm3，而利用本文模糊優(yōu)化設計方法得到的齒輪體積為2.639×106mm3，且均通過了疲勞強度校核。由此說明，本文模糊優(yōu)化設計方法的效果比傳統(tǒng)設計方法好。

綜上，當齒輪模數(shù)m=1.5 mm，小齒輪齒數(shù)z1=42，齒寬系數(shù)?=1.187 0時，直齒圓柱齒輪的體積最小，且可通過疲勞強度校核，優(yōu)化結果切實可行。

4 氣門彈簧的模糊優(yōu)化設計

內(nèi)燃機氣門彈簧［23，26］為圓柱螺旋彈簧，其最大變形量δmax=6.59 mm，工作載荷F=680 N，工作頻率fw=25 Hz，彈簧直徑d∈[2.5，6] mm，彈簧中徑D∈[30，60] mm，工作圈數(shù)N0∈[3，15]，旋繞比C∈[4，9]，長細比b∈[1，5.3]；彈簧材料為50CrVA，密度ρ=7.85×10-6kg/mm3，剪切模量G=80 GPa，許用切應力[τ]=450 MPa。

當氣門彈簧的截面為圓形時，其一階自振頻率fb為［27］：

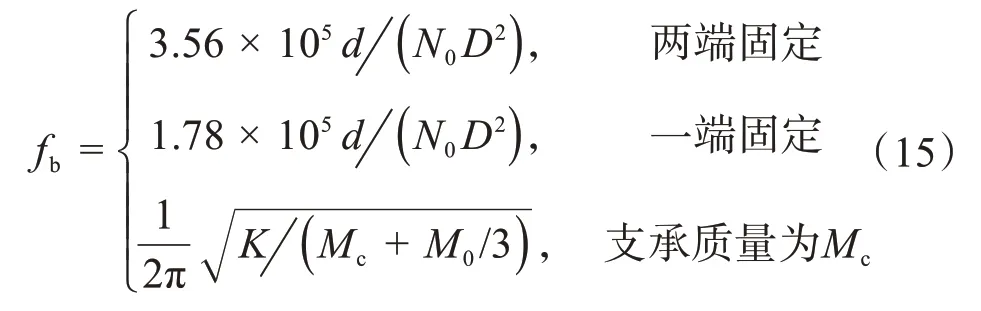
式中：K為彈簧剛度；M0為彈簧工作部分的質(zhì)量。

對于不同類型的彈簧，其自振頻率fb與工作頻率fw的關系為［27］：

以彈簧質(zhì)量最小為優(yōu)化目標，建立如下數(shù)學模型：

式中：δ為彈簧的變形量；［δ］為彈簧的許用變形量；τ為彈簧的應力；［fb］為彈簧的許用自振頻率。

對于氣門彈簧的許用應力，通常取擴增系數(shù)β=1.01，由擴增系數(shù)法得：。

對于氣門彈簧的自振頻率，通常取擴增系數(shù)β=0.95，基于[fb]=10fw=250 Hz，由擴增系數(shù)法得。

為方便計算，所有約束條件的隸屬函數(shù)均取線性隸屬函數(shù)。根據(jù)最優(yōu)水平截集法，上述約束條件可轉化為：

同樣采用云模型人工魚群算法、人工魚群算法和人工蜂群算法來求解氣門彈簧的模糊優(yōu)化問題。設人工魚群算法中的覓食次數(shù)為5，擁擠度為0.618；3種算法中的種群數(shù)量均為20，迭代上限為70次，最優(yōu)水平截集對應的參數(shù)λ*=0.4。基于3種算法的氣門彈簧模糊優(yōu)化的迭代過程如圖2所示，優(yōu)化結果如表5所示。

圖2 氣門彈簧模糊優(yōu)化的迭代過程Fig.2 Iteration process of fuzzy optimization for valve spring

由圖2和表5可知：

表5 氣門彈簧模糊優(yōu)化設計結果Table 5 Fuzzy optimization design results of valve spring

1）基于人工魚群算法的氣門彈簧模糊優(yōu)化目標函數(shù)呈階梯式下降趨勢，基于人工蜂群算法的呈逐漸下降趨勢，且下降速度較為均勻。

2）云模型人工魚群算法的收斂速度比人工魚群算法和人工蜂群算法更快。

3）基于云模型人工魚群算法優(yōu)化得到的氣門彈簧的質(zhì)量最小，優(yōu)于人工魚群算法和人工蜂群算法。

為了使云模型人工魚群算法優(yōu)化得到的氣門彈簧尺寸參數(shù)與尺寸系列中的數(shù)值相同，采用擬離散法中的交替查點法（又稱Luns法，常用于求解全離散變量優(yōu)化問題）［25］進行調(diào)整。由交替查點法求得氣門彈簧尺寸參數(shù)的最優(yōu)解為：直徑d=6 mm，中徑D=30 mm，工作圈數(shù)N0=2.75。此時，質(zhì)量M=0.099 kg，旋繞比C=5，長細比b=1.363，切應力τ=315.176 MPa，自振頻率fb=863.030 Hz，變形量δ=3.896 mm。該設計方案通過了疲勞強度校核，優(yōu)化結果切實可行。

5 結論

本文利用最優(yōu)水平截集法將模糊優(yōu)化設計問題轉變?yōu)槠胀▋?yōu)化設計問題，并采用云模型對人工魚群算法進行改進，然后結合增廣乘子法和云模型人工魚群算法對直齒圓柱齒輪和內(nèi)燃機氣門彈簧進行了模糊優(yōu)化設計，并與基于人工蜂群算法的優(yōu)化結果進行了對比，所得結論如下。

1）若罰因子較小，則增廣乘子法所得結果可能不滿足約束條件，因此應取較大的罰因子。外罰函數(shù)法的收斂性依賴于初始罰因子，且罰因子須逐步增大至無窮大，而增廣乘子法只須取1個較大的罰因子，并不要求趨向無窮大。

2）云模型中的正向云發(fā)生器可大幅提高人工魚群算法的全局尋優(yōu)能力。

3）利用本文模糊優(yōu)化設計方法得到的圓柱直齒齒輪的最小體積為2.620×106mm3，而利用傳統(tǒng)設計方法得到的齒輪體積為2.776×106mm3，且均通過了疲勞強度校核，說明本文模糊優(yōu)化設計方法所得的齒輪參數(shù)更為合理。同時，利用本文模糊優(yōu)化設計方法得到的氣門彈簧的尺寸參數(shù)符合要求。