復變函數斜軸橢球變換法的銜接應用

楊 力，姚德新

(1.蘭州交通大學 測繪與地理信息學院，甘肅 蘭州 730070；2.地理國情監測技術應用國家地方聯合工程研究中心，甘肅 蘭州 730070；3.甘肅省地理國情監測工程實驗室，甘肅 蘭州 730070)

隨著長大線路工程建設需求越來越多，對長大線路工程控制網的精度提出越來越高的要求。控制長度投影變形是長線工程施工質量的重要保證。文獻[1-5]提出法截面子午線高斯投影，有效的減小測區到中央子午線的距離，控制長度投影變形，解決高斯投影頻繁換帶、精度不高等問題，但該方法計算過程復雜、參數設置繁瑣。文獻[6-7]提出斜軸變形橢球高斯投影，利用空間直角坐標的優越性及便利性大大減小測區的高斯投影橫坐標，有效降低高差帶來的影響。文獻[8-10]提出采用大橢圓線橢球高斯投影，優化計算，數據處理效率高，同樣適用于長線工程。在長度投影變形分析中，滿足投影變形不大于10 mm/km的條件下，測區平均高程大于63.71 m時需考慮由高程引起的長度變形，測區距中央子午線距離大于28.5 km時，需考慮投影引起的長度變形。但是文獻[2-10]所提出的多種方法在線路經過地勢復雜區域時，線路轉折大、高差大，導致部分測區邊緣距斜軸橢球中央子午線較遠平均高程大的問題，此時一個工程橢球并不能滿足綜合投影變形不大于10 mm/km的要求，需對線路進行平面、高程分段處理。文獻[11]提出交點法線重合的方法，面對轉折大的長線工程分成多段子午線法截面橢球進行平面銜接。文中在斜軸變形橢球高斯投影理論的基礎上提出復變函數斜軸橢球變換法高斯平面坐標微分公式，構建斜軸橢球變換前后高斯平面坐標轉換模型，并通過實際鐵路工程數據驗證該模型在坐標系的銜接，以及建立高精度工程控制網中的優越性與適用性。

1 復變函數高斯平面坐標的微分公式推導

高斯投影正解的非迭代復變函數表示[12-13]：

q=arctanh(sinB)-e·arctanh(e·sinB)，

w=q+il，

φ=arcsin(tanh(w))，

z=x+iy=a(j0φ+j2sin2φ+j4sin4φ+

j6sin6φ+j8sin8φ+j10sin10φ)，

x=Rez,y=lmz.

(1)

式中：q為等量緯度；w為投影前等量緯度與經差組成的復變量；z為高斯投影后平面縱橫坐標組成的復變量，其中x為縱坐標，y為橫坐標；B，l為大地緯度，經差；e為第一偏心率；a為橢球長半軸。Re為復數實部，Im為復數虛部。

復變量z分別對參數(a，e，B，l)求微分：

(2)

中間量偏導數：

(3)

(4)

(5)

(6)

矩陣中各偏導數：

j6sin6φ+j8sin8φ+j10sin10φ),

(7)

2j2cos2φ+4j4cos4φ+6j6cos6φ+8j8cos8φ

+10j10cos10φ)],

(8)

6j6cos6φ+8j8cos8φ+10j10cos10φ),

(9)

6j6cos6φ+8j8cos8φ+10j10cos10φ).

(10)

2 橢球變換法大地坐標與高斯坐標微分公式

2.1 橢球膨脹法大地坐標與高斯坐標微分公式

橢球膨脹法：橢球中心、軸向、橢球偏心率e保持不變，橢球長短半軸發生變化。橢球長半軸變化da=a1-a0。采用高程直接補償法，選取da=△H0。

膨脹橢球大地坐標微分公式[2]：

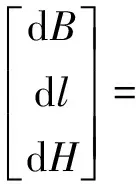
(11)

膨脹橢球高斯坐標微分公式：

(12)

2.2 橢球平移法大地坐標與高斯坐標微分公式

橢球平移法：將橢球以橢球中心平移，不改變橢球的軸向、長半徑、偏心率、尺度。

平移橢球大地坐標微分公式[2]：

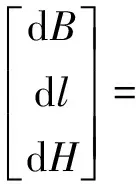
(13)

平移橢球高斯坐標微分公式：

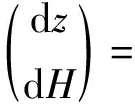
(14)

2.3 橢球變形法大地坐標與高斯坐標微分公式

橢球變形法：橢球的長半徑、偏心率改變，而不改變橢球的軸向、中心、尺度。

變形橢球大地坐標微分公式[2]：

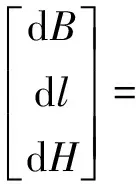
(15)

變形橢球高斯坐標微分公式：

(16)

3 高斯平面坐標銜接模型

根據復變函數高斯平面坐標微分公式與橢球變換法大地坐標微分公式構建高斯平面坐標銜接模型:

(17)

式中：z1，z2為橢球變換前后高斯平面坐標復變量；dx，dy為復變函數高斯平面坐標微分公式計算的高斯平面坐標的位移量；(x1，y1)和(x2′，y2′)為橢球變換前后的高斯平面坐標。

4 算例分析

文中數據來源于文獻[2,6]中的算例分析。根據“某鐵路控制測量成果報告”的內容，正線方案長約500 km，測區位于86°00′E～95°30′E，36°00′N～42°00′N，線路海拔高程最大為3 163.6 m，最小為2 797.8 m[2,6]。11個測站點在基礎橢球E0(CGCS2000)上的線路走向如圖1所示。由于篇幅所限，文中選取較好表達線路走向的6個測站點(1、7、8、9、10、11號點)數據進行算例分析。依據斜軸變形橢球高斯投影理論，利用最小二乘法，空間坐標系旋轉，將基礎橢球E0變換到斜軸橢球E1上。6個測站點在斜軸橢球E1上的大地坐標以及在E1橢球參數下的高斯平面坐標見表1。斜軸橢球E1長半軸a1為6 378 137 m，偏心率e1為0.058 134 977 515 3。

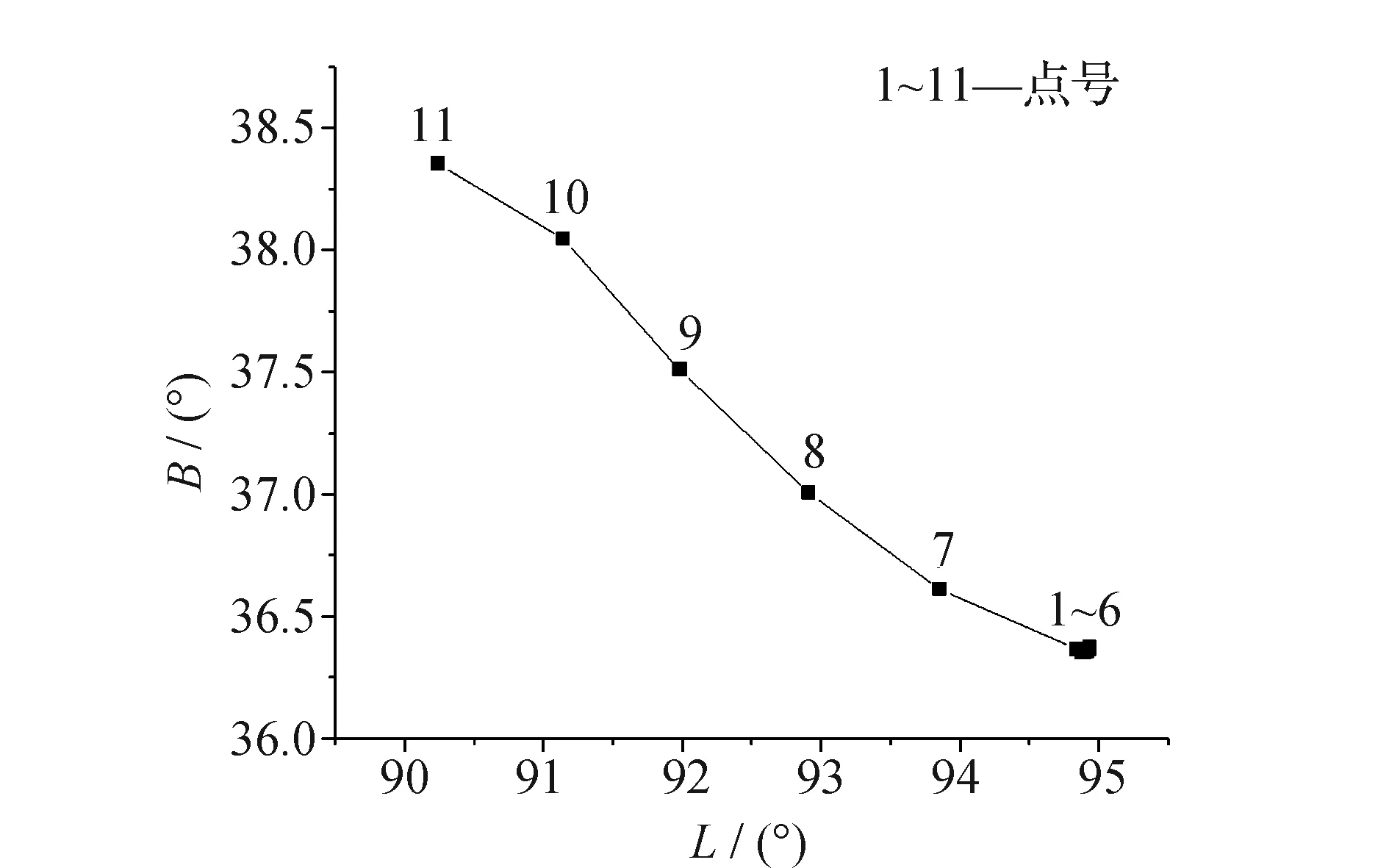
圖1 線路走向測點分布圖

4.1 斜軸膨脹橢球

在斜軸橢球E1的基礎上，根據橢球膨脹法[14-15]將斜軸橢球E1膨脹到E2橢球，見圖2。各點在E2橢球上的投影面高程、大地坐標、高斯平面坐標(x2，y2)以及長度投影變形，見表2。通過復變函數高斯平面微分公式計算高斯平面經橢球變換前后高斯平面坐標位移量(dx，dy)，高斯平面坐標銜接模型計算膨脹后高斯平面坐標(x2′，y2′)。通過(x2，y2)與(x2′，y2′)的較差進行精度檢驗，x2坐標誤差小于15.5 mm，y2坐標誤差不大于0.07 mm，見表3。

圖2 斜軸膨脹橢球及高斯平面坐標

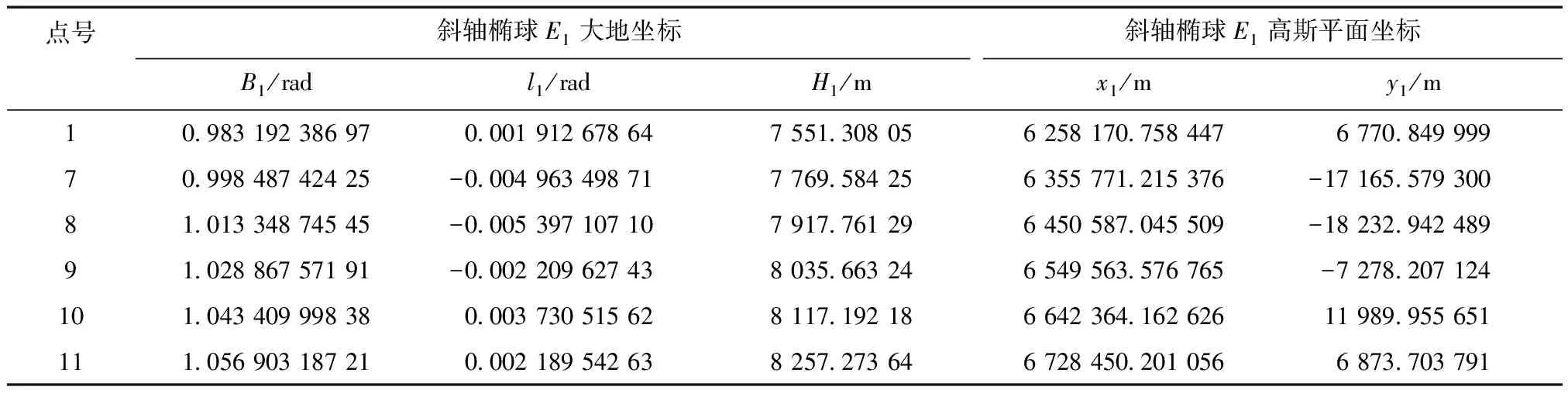
表1 E1大地坐標與高斯平面坐標

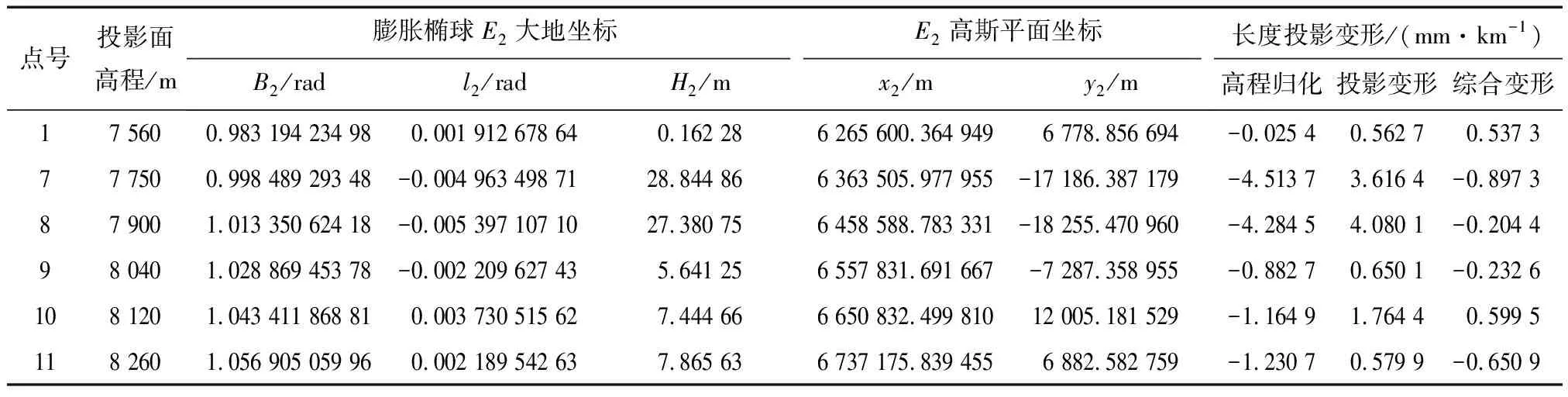
表2 斜軸膨脹橢球高斯投影

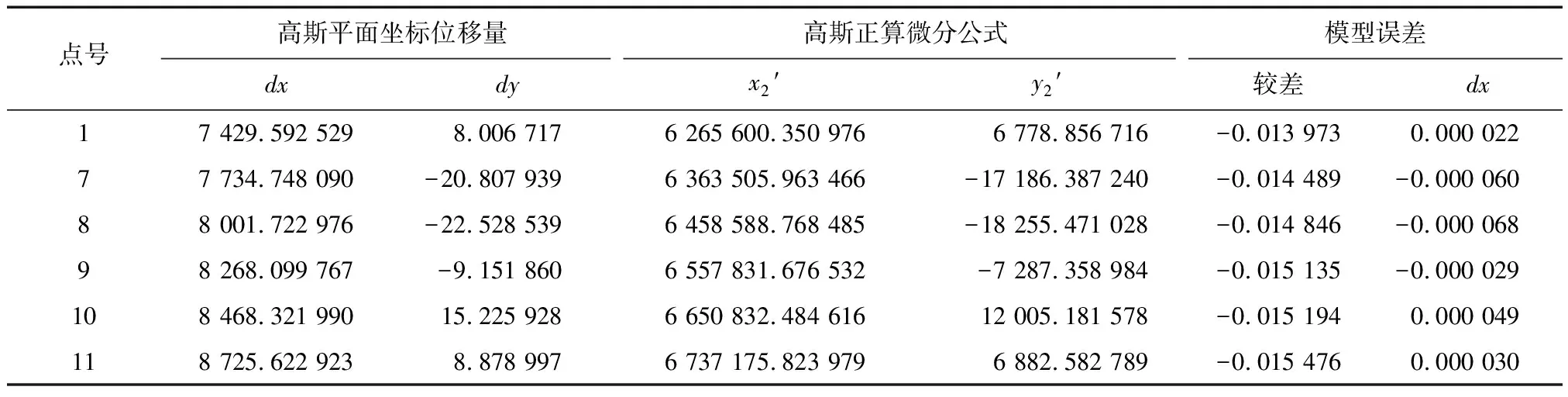
表3 斜軸膨脹橢球高斯平面坐標銜接模型誤差分析 m

面對地勢復雜地區線路高差大，會導致長度投影變形高程歸化改正超限的情況，需根據不同的投影面高程進行膨脹。選取1號點，進行不同投影面高程橢球膨脹，根據投影面高程的差值可計算橢球膨脹前后高斯平面坐標位移量。膨脹橢球投影高程面高差小于100 m時，橢球膨脹前后高斯平面銜接模型誤差小于0 mm；投影高程面高程差值為9 000 m的時候，橢球膨脹前后高斯平面銜接模型誤差小于0.026 mm，見表4。在滿足投影變形的條件下，選擇合適的高程投影面，不同投影面高程膨脹橢球高斯平面坐標可以兩兩轉換。

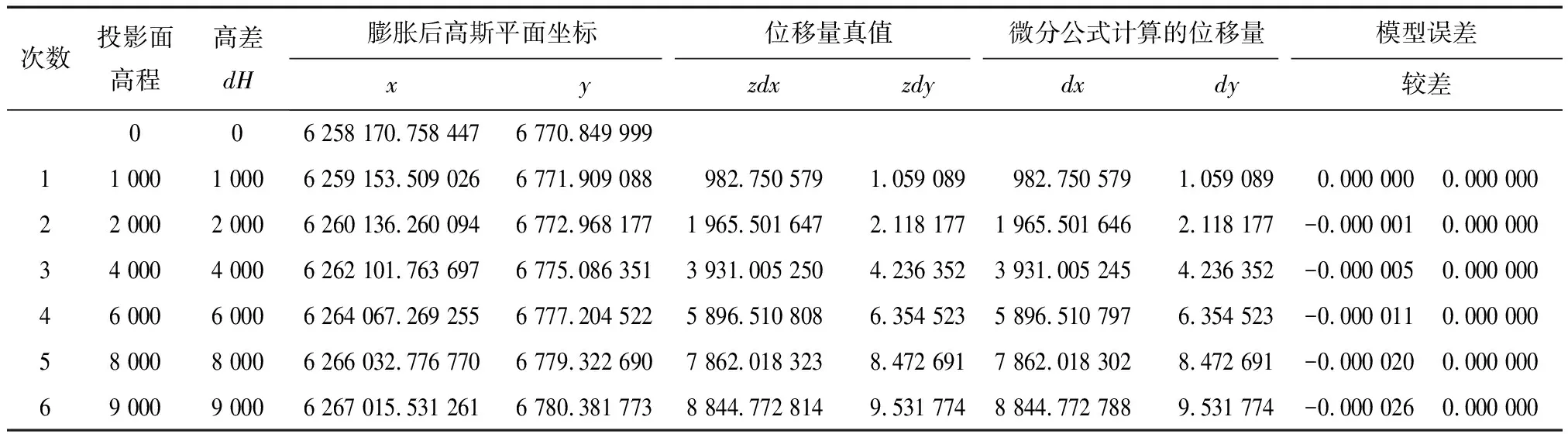
表4 斜軸橢球不同高程投影面高斯平面坐標銜接模型誤差分析 m

4.2 斜軸平移橢球

利用橢球平移法[14-15]將斜軸橢球E1平移到E3橢球，見圖3。E3橢球參數與斜軸橢球E1一致。此時點在E3橢球上的大地坐標、高斯平面坐標(x3，y3)，長度投影變形見表5。通過復變函數高斯平面微分公式計算經橢球變換前后高斯平面坐標位移量dx，dy，高斯平面坐標銜接模型計算平移后高斯平面坐標(x3′，y3′)。通過(x3，y3)與(x3′，y3′)的較差進行精度檢驗，高斯平面坐標銜接模型x坐標誤差不大于1.7 mm，y坐標誤差不大于10.9 mm，見表6。

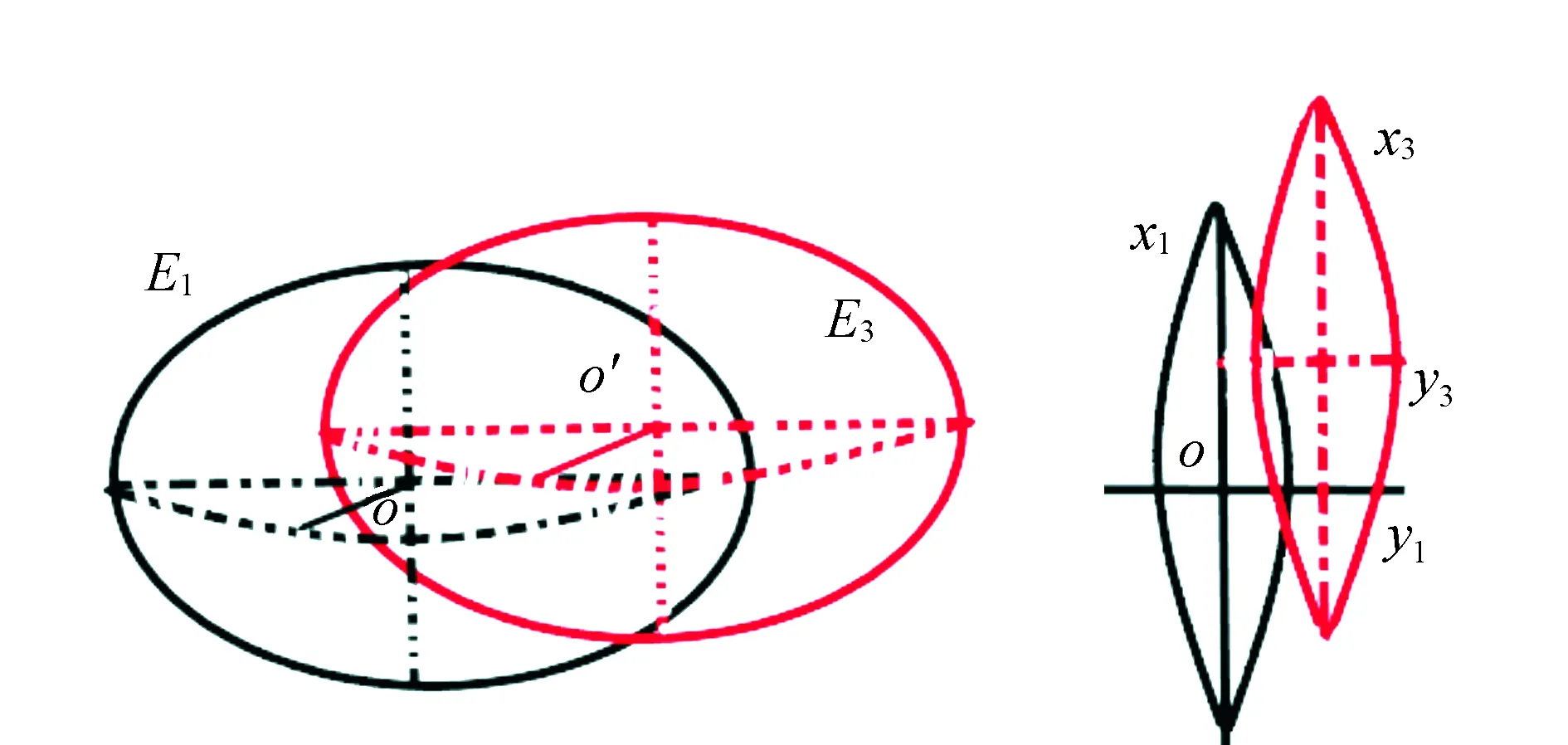
圖3 斜軸平移橢球及高斯平面坐標

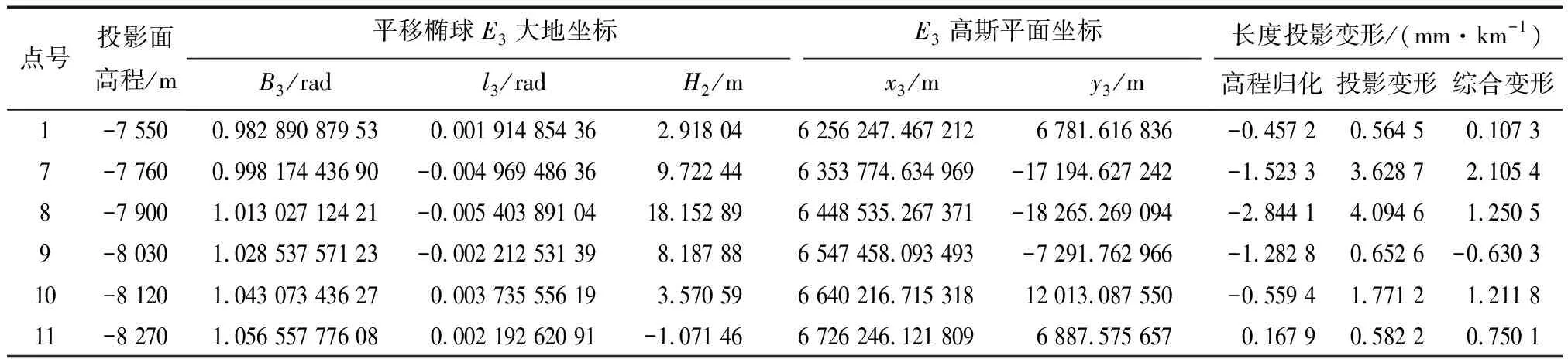
表5 斜軸平移橢球高斯投影

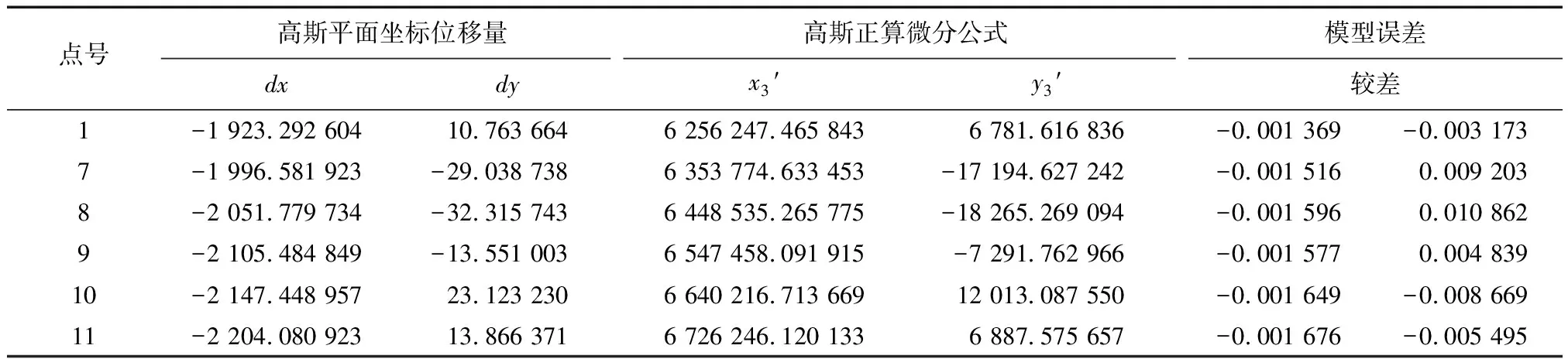
表6 高斯平面坐標銜接模型誤差分析m

4.3 斜軸變形橢球

利用橢球變形法[14-15]將斜軸橢球E1變形到E4橢球，見圖4。點在E4橢球上的投影面高程、大地坐標以及高斯平面坐標(x4，y4)，長度投影變形小于10 mm/km，見表7。通過復變函數高斯平面微分公式計算經橢球變換前后高斯平面坐標位移量dx，dy和高斯平面坐標銜接模型計算平移后高斯平面坐標(x4′，y4′)。通過(x4，y4)與(x4′，y4′)的較差進行精度檢驗，高斯平面坐標銜接模型x坐標誤差小于16 m，y坐標誤差不大于0.026 mm，見表8。

圖4 斜軸變形橢球及高斯平面坐標

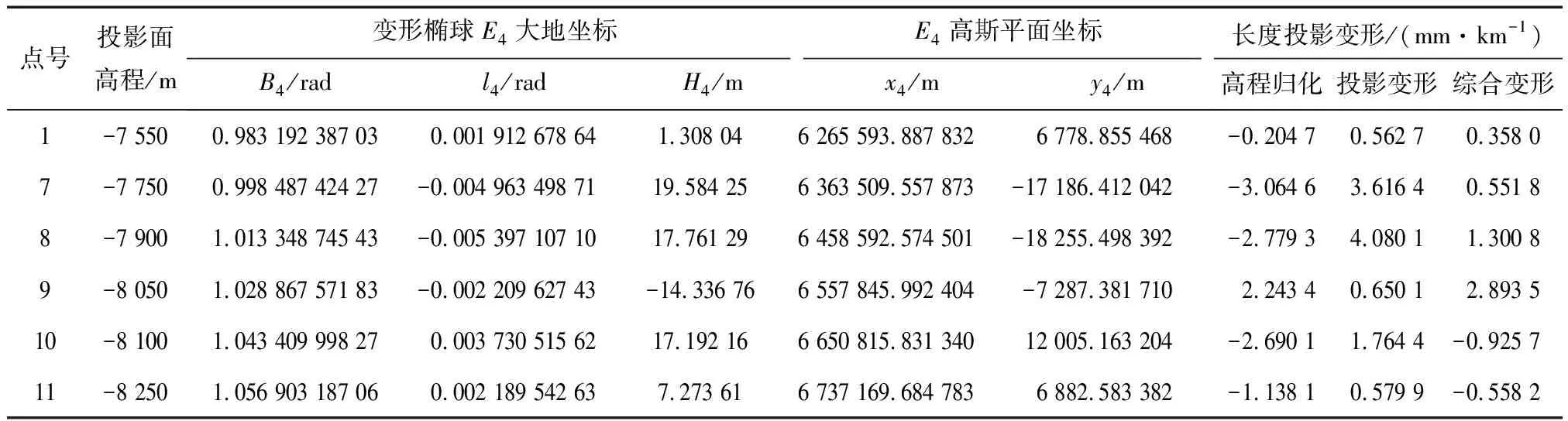
表7 斜軸變形橢球高斯投影

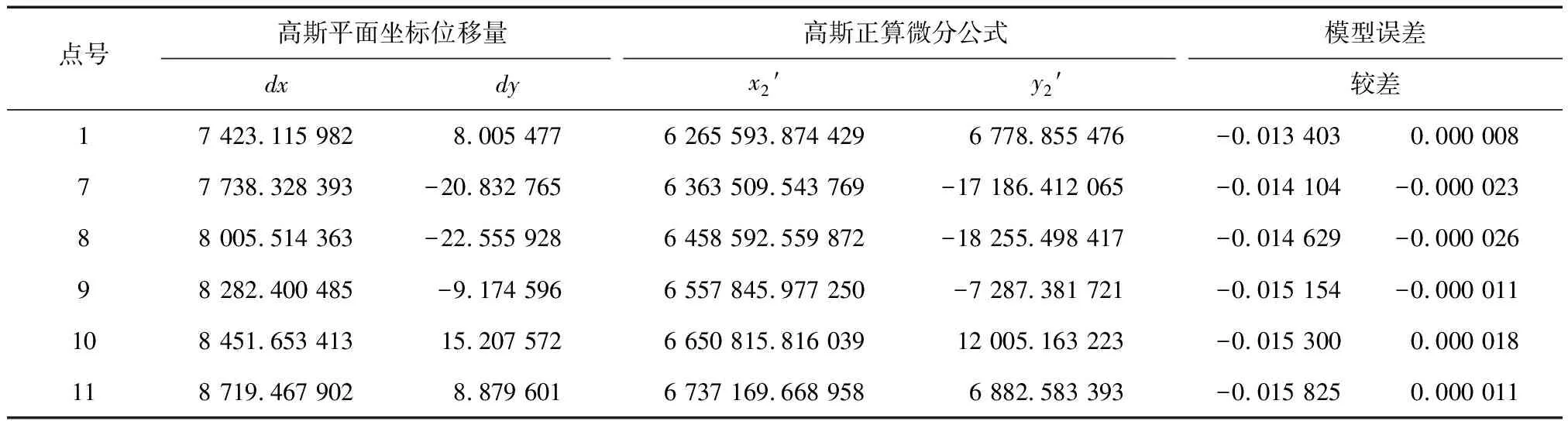
表8 高斯平面坐標銜接模型誤差分析m

5 結束語

文中以復變函數求偏導數推導高斯平面坐標微分公式，構建高斯平面坐標轉換模型，并結合實際鐵路工程數據進行分析，得出如下結論：

1)高斯平面坐標銜接模型在斜軸平移橢球中精度最高誤差小于10.9 mm，其次是斜軸膨脹橢球誤差小于15.5 mm，斜軸變形橢球最大誤差為16 mm。由誤差分析可知，通過誤差改正模型可將高斯平面坐標銜接模型的精度進一步提高。同時涉及橢球參數變化量大小、橢球變換基準點的選取、提高投影面高程精確值等。

2)面對轉折大、高差大的長線路工程，所構建的多個工程橢球利用橢球變換參數值即可計算橢球變換前后高斯平面的坐標位移量，并可進行橢球變換前后的高斯平面坐標銜接。

3)較大的投影面高程橢球膨脹，高斯平面銜接模型誤差小于0.026 mm，在滿足投影變形的條件下，選擇合適的高程投影面，不同投影面高程膨脹橢球高斯平面坐標可以兩兩轉換，驗證高斯平面坐標銜接模型的正確性與優越性。

4)利用Mathematica數學軟件推導復變函數高斯平面微分公式以及構建高斯平面坐標銜接模型，可編制相關軟件，投入工程使用。