高考中應用題瓶頸突破

摘 要：一直以來，數學都是一門難度相對較大的科目，尤其是在高中教育階段，隨著知識深度與廣度的同步提升，題目難度也隨之增加，應用題更是難上加難，而且在高考中所占的分值比例較大，學生在解題中極易遇到瓶頸難易突破，影響他們的解題效率與自信.本文針對如何突破高考中應用題瓶頸作探討，以江蘇高考應用題為例，并提出部分個人建議.

關鍵詞：高考;應用題;瓶頸突破;江蘇

中圖分類號：G632 ? ? ?文獻標識碼：A ? ? ?文章編號：1008-0333（2021）22-0032-02

收稿日期：2021-05-05

作者簡介：尤蓓君（1982.6-），女，江蘇省江陰人，本科，中學一級教師，從事高中數學教學研究.

應用題是用語言或文字敘述有關事實，反映某種數學關系，并求解未知數量的題目，每道應用題都包括已知條件和所求問題.在數學高考中，應用題不僅是一個常設題型，還占據著較大的分值比例，學生雖然從小學階段就開始接觸應用題，不過高考中的應用題難度系數較大，教師需指導他們從具體的邏輯思維出發，使其認真分析題目內容，真正突破瓶頸.

一、高度重視審題環節，做好應用題解題準備

高考數學應用題涉及題材廣泛，背景也呈現出多樣的色彩，一般情況下，文字敘述較長，數據多、不規則，文字、符號及其相關關系式相互交織，顯得復雜、繁瑣.要想突破高考中數學應用題的瓶頸，教師首先需要求學生高度重視審題環節，認真閱讀題目信息，細致、耐心的審題，使其學會去粗取精，抓住題目的主干，同時挖掘出隱含條件，做好準備工作.

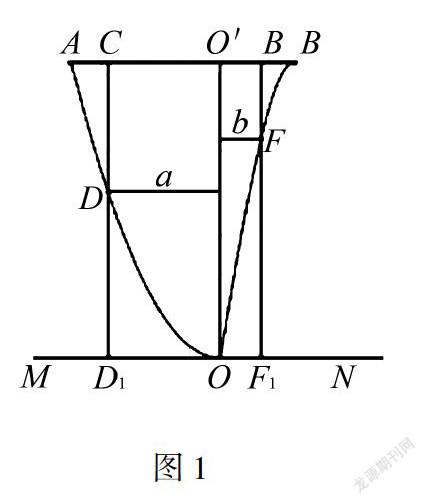
例1 某地準備在山谷中建一座橋梁，橋址位置的豎直截面圖如圖1所示：谷底O在水平線MN上，橋AB與MN平行，OO′為鉛垂線（O′在AB上），經測量，左側曲線AO上任一點D到MN的距離h1（米）與D到OO′的距離a（米）之間滿足關系式h1=140a2;右側曲線BO上任一點F到MN的距離h2 （米）與F到OO′的距離 b（米）之間滿足關系式h2=-1800b3+6b.已知點B到OO′的距離為40米.

（1）求橋AB的長度;

（2）計劃在谷底兩側建造平行于OO′的橋墩CD和EF.且CE為80米，其中C，K在AB上（不包括端點）.橋墩EF每米造價k（萬元）.橋墩CD每米造價32k（萬元）（k>0），問O′E為多少米時，橋墩CD與EF的總造價最低？

教師引領學生仔細閱讀題，使其找出關鍵信息、已知與未知條件，弄懂文字與符號的含義，做好解題準備.

二、識別實際問題模式，確定應用題解題思路

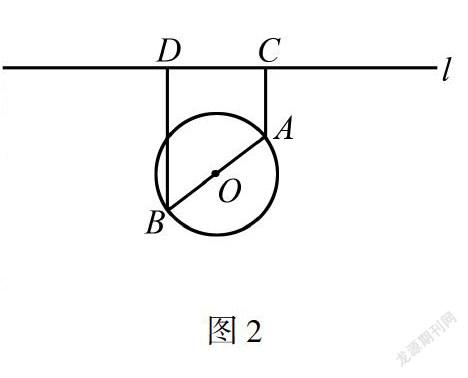
應用題本身反映的就是實際生活中的相關事實，針對高考數學應用題中的瓶頸而言，教師需引領學生對實際問題的模式進行識別.圖2

例2 如圖2，一個湖的邊界是圓心為O的圓，湖的一側有一條直線型公路l，湖上有橋AB（AB是圓O的直徑）.規劃在公路l上選兩個點P、Q，并修建兩段直線型道路PB、QA.規劃要求：線段PB、QA上的所有點到點O的距離均不小于圓O的半徑.已知點A、B到直線l的距離分別為AC和BD（C、D為垂足），測得AB=10，AC=6，BD=12（單位：百米）.

（1）若道路PB與橋AB垂直，求道路PB的長;

（2）在規劃要求下，P和Q中能否有一個點選在D處？并說明理由;

（3）對規劃要求下，若道路PB和QA的長度均為d（單位：百米）.求當d最小時，P、Q兩點間的距離.

本題屬于典型的測量題，教師引領學生聯系到三角函數的知識，并結合圓、平面直角坐標系、斜率、兩點距離公式等確定思路，讓他們順利解題.

三、運用數形結合思想，優化應用題解題過程

數和形作為數學中兩個作為古老與基本的研究對象，兩者在一定條件下能夠相互轉化，高中數學主要研究的也是這兩大部分，代數對應的是“數”，幾何則與“形”相對應，應用題也是圍繞著兩個方面設置的.因此，為實現高考中數學應用題的瓶頸突破，教師應指導學生運用數形結合思想分析和處理應用題，促使他們通過以數解形或以形助數優化解題過程.

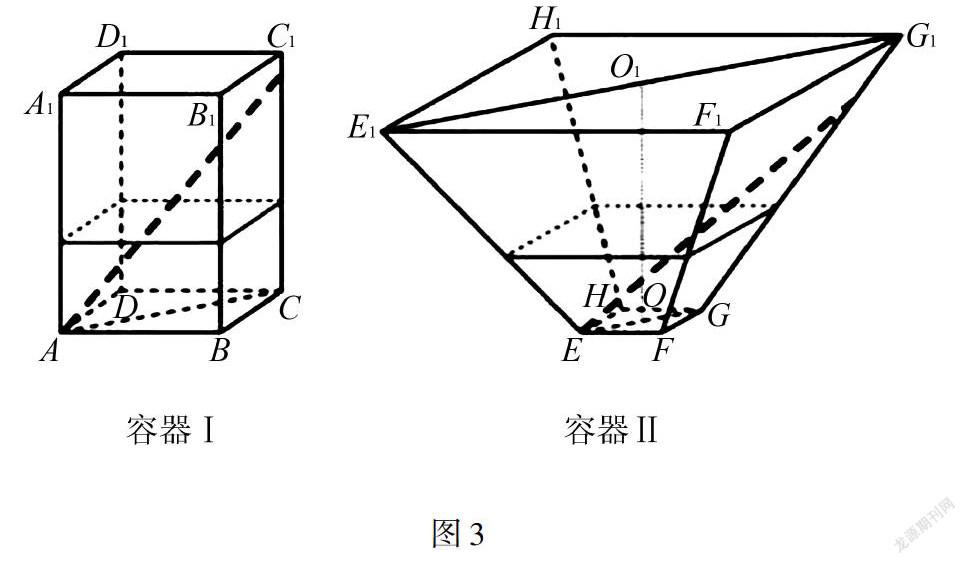
例3 如圖，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm，容器Ⅰ的底面對角線AC的長為107cm，容器Ⅱ的兩底面對角線EG，E1G1的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水，水深均為12cm.現有一根玻璃棒l，其長度為40cm（容器厚度、玻璃棒粗細均忽略不計）.

（1）將l放在容器Ⅰ中，l的一端置于點A處，另一端置于側棱CC1上，求l沒入水中部分的長度;

（2）將放在容器Ⅱ中，l的一端置于點E處，另一端置于側棱GG1上，求沒入水中部分的長度.

本題考查玻璃棒l沒入水中部分長度的求法，學生可用數形結合思想、化歸與轉化思想分析題目，結合空間中線線、線面、面面間的位置關系等基礎知識來解題，優化他們的解題過程，使其推理論證、運算求解、空間想象能力得以鍛煉.

四、積極建立數學模型，把握解決應用題關鍵

數學建模就是根據實際問題來建立數學模型，對數學模型來進行求解，再根據結果去解決實際問題，而應用題大部分都是實際問題，這為數學模型思想的應用提供良好契機.從本質上來講，在高中數學中，應用題同實際生活聯系的最為密切，解題的關鍵在于數學模型的建立，教師需意識到這一點，指引學生積極建立數學模型，使其把握應用題的解題關鍵.

例4 某農場有一塊農田，如圖所示，它的邊界由圓O的一段圓弧（P為此圓弧的中點）和線段MN構成.已知圓O的半徑為40米，點P到MN的距離為50米.現規劃在此農田上修建兩個溫室大棚，大棚Ⅰ內的地塊形狀為矩形ABCD，大棚Ⅱ內的地塊形狀為△CDP，要求A，B均在線段MN上，C，D均在圓弧上，設OC與MN所成的角為θ.

（1）用θ分別表示矩形ABCD和△CDP的面積，并確定sinθ的取值范圍;

（2）若大棚Ⅰ內種植甲種蔬菜，大棚Ⅱ內種植乙種蔬菜，且甲、乙兩種蔬菜的單位面積年產值之比為4∶3，求當為何值時，能使甲、乙兩種蔬菜的年總產值最大.

本題主要考查三角函數的應用、用導數求最值等基礎知識，以及直觀想象和數學建模能力，教師要指引學生建立數學模型，使其運用所學知識分析與解決這一實際問題.

總而言之，在數學應用題具有相當高的實踐考察價值，可以檢測學生對知識點的掌握與運用情況，其實高考數學應用題并非像想象中那樣不可逾越，教師需指導他們認真審題、正確運用解題方法，最終在高考中獲得理想的成績.

參考文獻：

[1]張玲玲.從高考數學應用題變化規律探討教學策略[J].數學學習與研究，2020（08）：40.

[2]王艷梅.淺談高考數學應用題變化對高中數學教學的影響[J].考試周刊，2019（42）：103.

[3]孫霞.高中數學應用題在高考中如何突破[J].考試周刊，2017（43）：99.

[責任編輯：李 璟]