基于二端口散射參數的CVT寬頻暫態(tài)模型

潘 飛，穆 舟，劉 浩，王彤彤，江 波,張 榆，張晨萌，謝施君，林國松

(1.西南交通大學電氣工程學院，四川 成都 611756；2.國網四川省電力公司電力科學研究院，四川 成都 610041；3.清華大學電機工程與應用電子技術系，北京 100084；4.山東泰開互感器有限公司，山東 泰安 271000；5.國網四川省電力公司計量中心，四川 成都 610045)

0 引 言

電壓互感器是電力系統(tǒng)中必不可少的測量設備，其將一次系統(tǒng)和二次系統(tǒng)電氣隔離開，以便在二次側對系統(tǒng)進行測量和保護等工作。目前，國內外電力系統(tǒng)大量投入使用的電壓互感器主要包含電磁式電壓互感器和電容式電壓互感器兩種。其中電容式電壓互感器(capacitive voltage transformer，CVT)由于其絕緣強度高、不易發(fā)生鐵磁諧振且價格較低等優(yōu)點被廣泛運用于110 kV以上的電網中[1]。

在研究過電壓保護問題時，暫態(tài)過電壓包含豐富的非工頻頻率分量，而之前廣泛運用的CVT在線監(jiān)測系統(tǒng)不能滿足非工頻暫態(tài)電壓的CVT的寬頻測量。因此CVT寬頻模型的建立一直是眾多學者專家研究的重點。準確的CVT寬頻模型的建立對于雷電過電壓、操作過電壓的測量和電磁兼容問題有著重要的意義。

1 CVT的寬頻模型

如圖1所示,CVT主要由電容單元和電磁單元兩部分組成。其中電容單元主要由高壓電容C1和中壓電容C2串聯組成。電容單元將高電壓電壓波形轉換為10～20 kV中壓電壓波形輸入電磁單元。電磁單元由中間變壓器、補償電抗器L、阻尼器D、避雷器BL等組成。為了減小負荷對中壓電壓的影響，電磁單元的中壓側接入一個補償電抗器,其在工頻電壓下與電容單元的中壓點阻抗諧振。

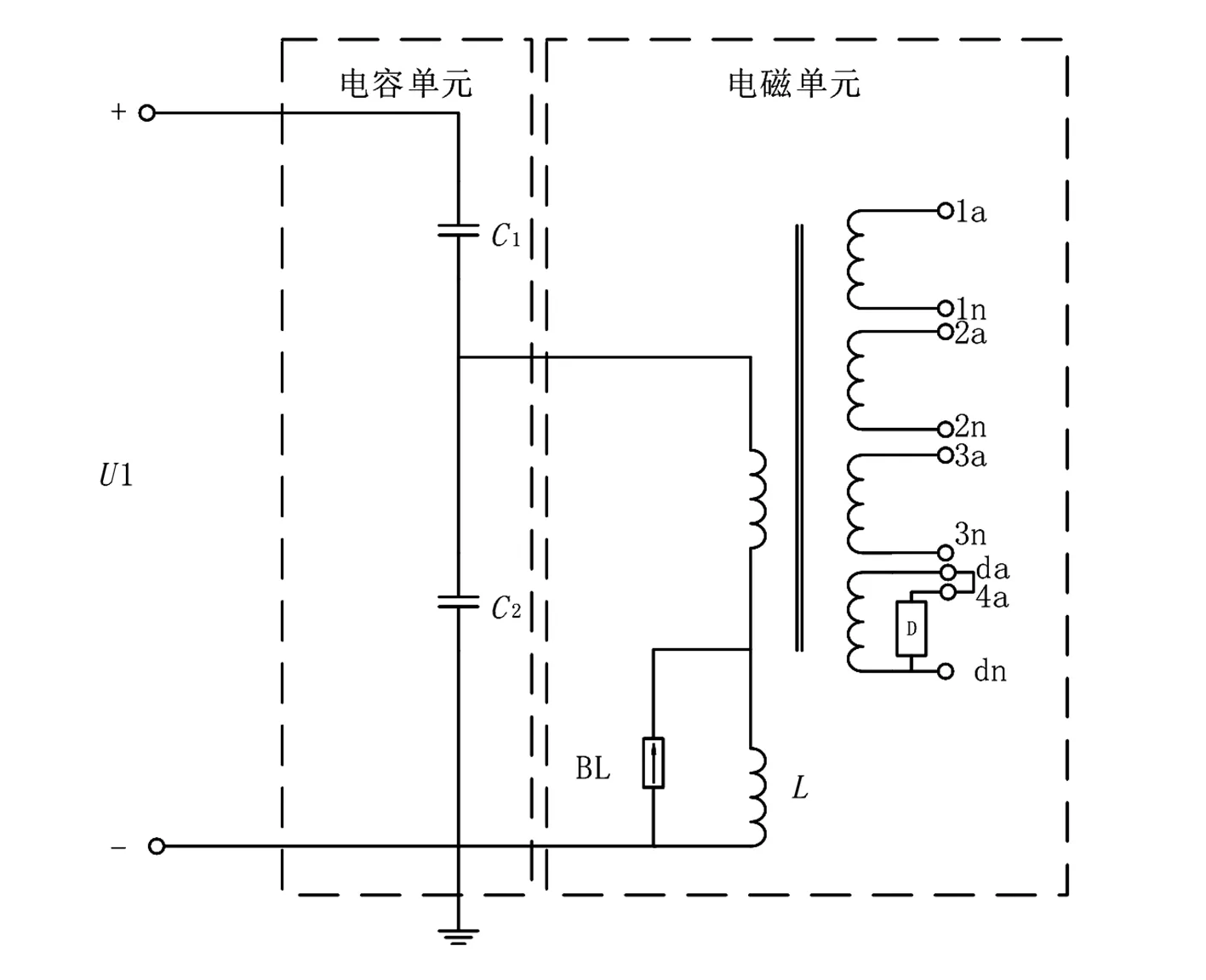
圖1 CVT穩(wěn)態(tài)物理模型

圖1所示的模型為CVT的穩(wěn)態(tài)物理模型。該模型能夠準確地體現工頻電壓下CVT的工作情況。而具有高頻成分的暫態(tài)電壓還將受制于CVT內部復雜的雜散參數以及元件之間的耦合等效應。由于傳統(tǒng)的CVT穩(wěn)態(tài)物理模型無法囊括這些效應，因此需要構建新的CVT寬頻暫態(tài)模型來反應CVT的暫態(tài)電壓傳遞特性。

采用圖2所示的π型黑盒模型來構建CVT寬頻暫態(tài)模型。

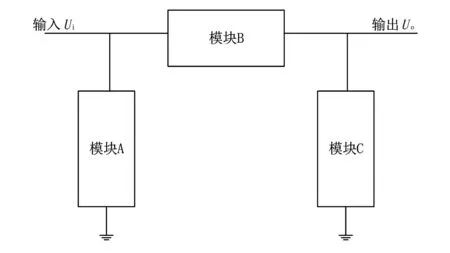
圖2 CVT黑盒模型

CVT黑盒模型由3個子模塊構成，子模塊內部均由傳統(tǒng)的R、L、C元件構成。整個模型基于準確測量得到的端口寬頻參數來構建，而不必得到物理模型中各個元件的準確參數。

CVT的π型黑盒建模的步驟如下：

1)測量待測件端口之間的寬頻二端口散射參數(S參數)，并轉化為二端口導納參數(Y參數)。運用矢量匹配法將Y參數擬合成有理數表達式，并進行端口無源優(yōu)化。

2)基于二端口Y參數，計算各個子模塊的單端口導納參數的有理數表達式。

3)基于各個子模塊的導納參數的有理數表達式，進一步用電路綜合理論建立等值電路模型。

2 CVT二端口寬頻參數的測量與計算

2.1 寬頻參數的獲取

首先運用網絡分析儀測量CVT輸入、輸出端口的二端口S參數。如圖3所示，二端口S參數的4個子參數分別代表著在功率歸一化后，兩個端口各自的反射參數與兩個端口之間的傳輸參數，可分別用式(1)計算。

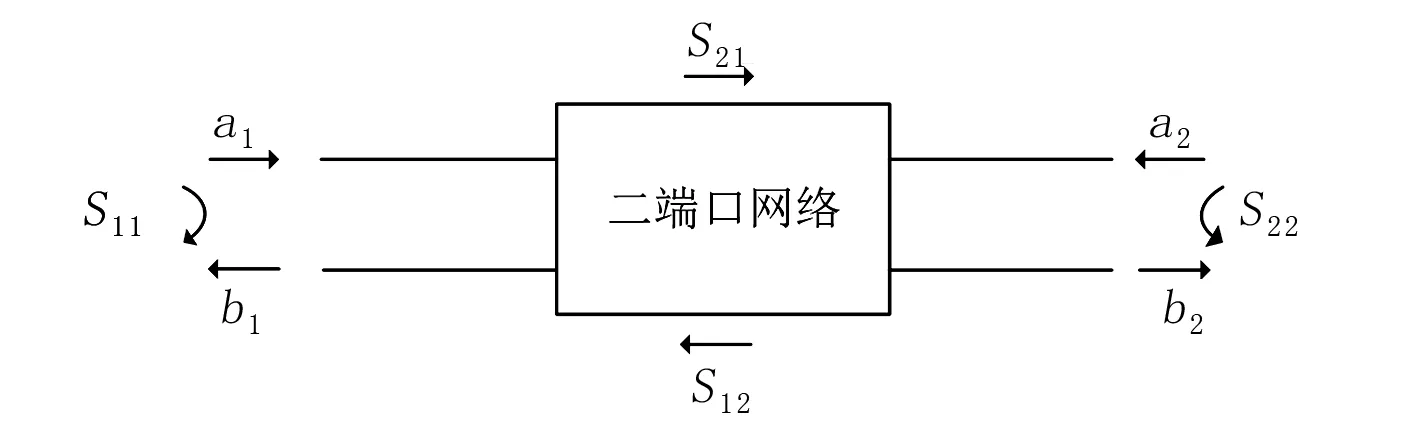
圖3 S參數

(1)

圖4 AGILENT E0571C對CVT的測量

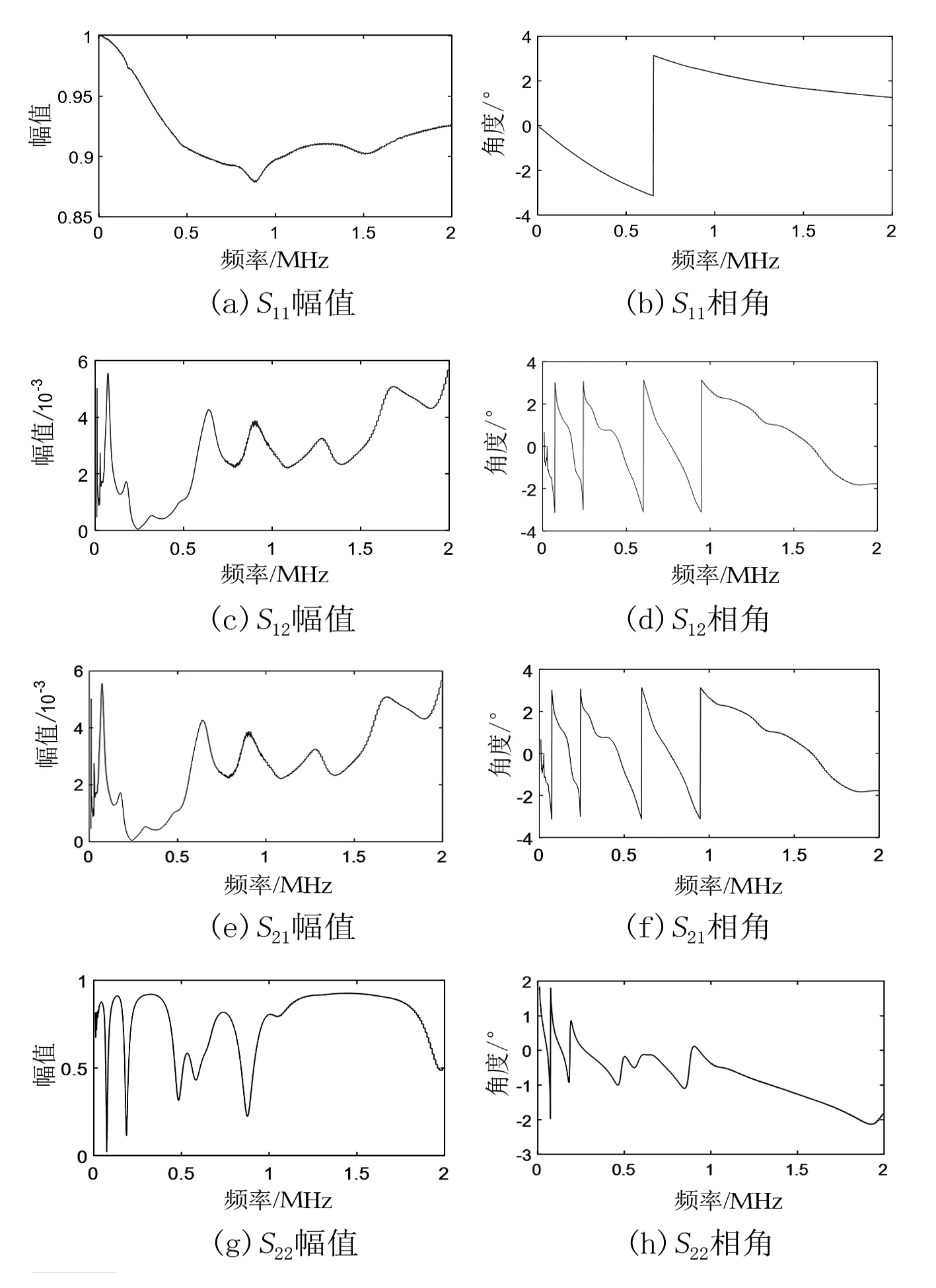
圖5 S參數測量結果

獲取S參數后，運用式(2)[2]將S參數轉換為CVT的Y參數。其中Z01、Z02為端口匹配阻抗，由于實驗中使用的同軸電纜以及各端口的特征阻抗均為50 Ω，因此端口匹配阻抗也取50 Ω。

2.2 Y參數的矢量匹配擬合和無源優(yōu)化

對于上一步獲取的一定頻率范圍內CVT二端口Y參數，其必須擬合為有理數表達式才能進一步地處理。這里采用矢量匹配法對Y參數進行有理數表達式擬合。

矢量匹配法[6-8]是一種能快速收斂且能保持函數穩(wěn)定性的有理函數擬合方法，由B.Gustavsen于1999年提出。矢量匹配法簡潔、快速、穩(wěn)定且無數值病態(tài)問題，被廣泛運用于宏模型提取方法和頻域線性系統(tǒng)擬合等方向。矢量匹配法將上面測量得到Y11、Y12、Y21、Y22進行有理數擬合，分別表達為如式(3)的有理數分式和形式：

(3)

式中：留數ci和極點ai為實數或共軛復數對；而常數項d和比例項e為實數且為可選項，這里忽略，即e=0,d=0；N為總支路數。

這樣矢量匹配的問題就轉化為如何得到式(3)中各項系數的估計值來求得f(s)的最小二乘估計。由于未知極點ai在分母，則式(3)對未知數來說是非線性求解問題。矢量匹配法通過引入初始極點將非線性求解問題分解為兩步連續(xù)的線性問題來求解。

對測得的S參數進行矢量匹配的結果如圖6和圖7所示，匹配的誤差在10-4以下，表明匹配的結果較為精準。

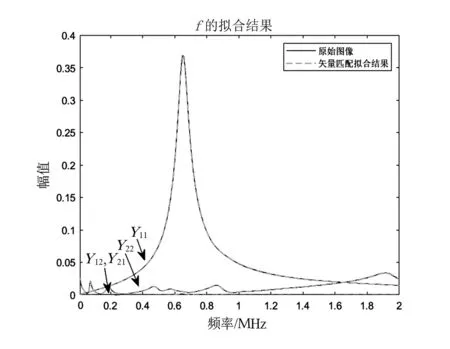
圖6 幅值匹配結果

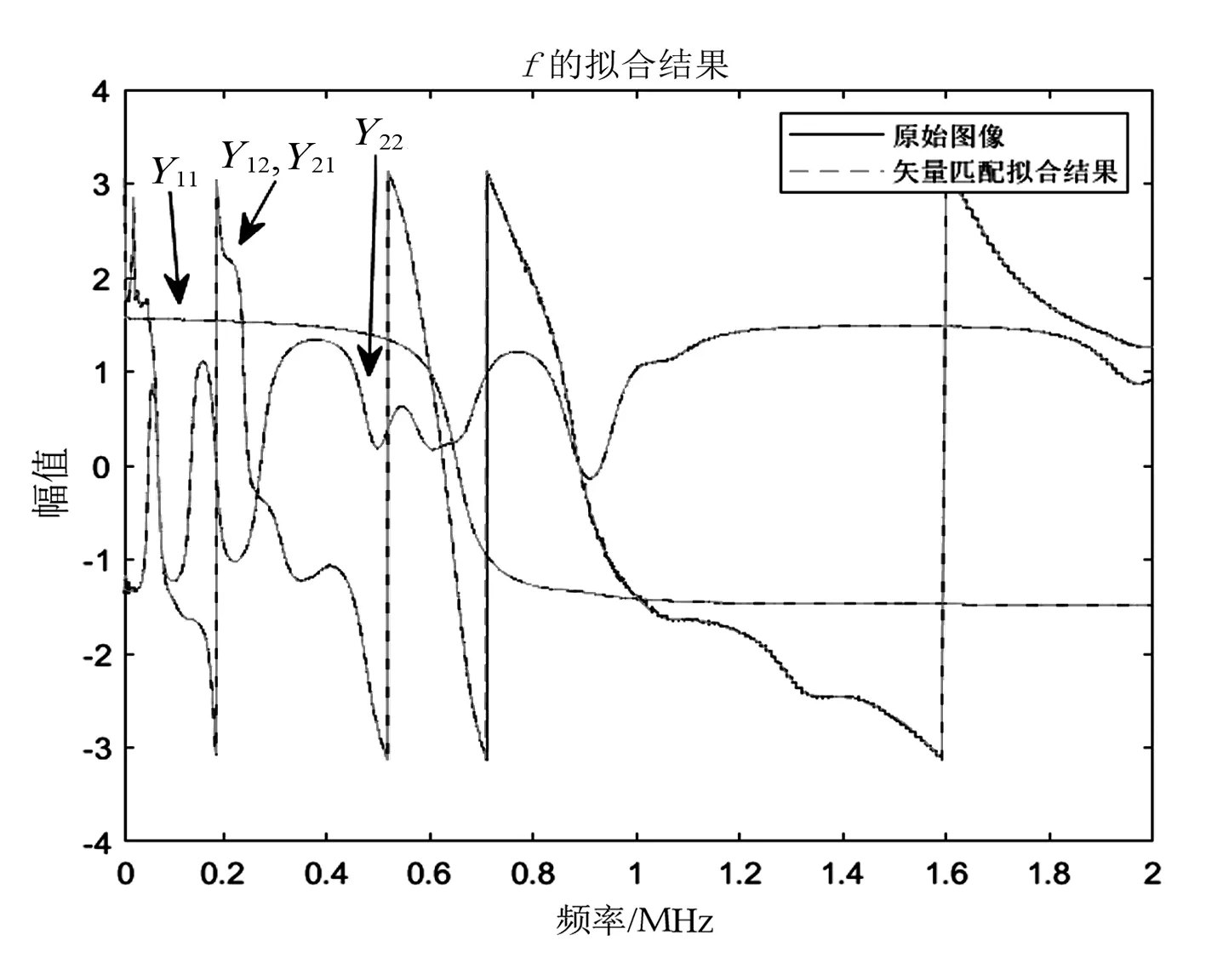
圖7 相角匹配結果

矢量匹配法能夠保證擬合結果的穩(wěn)定性(極點實部小于0)，但是無法保證其結果的無源性。而有源的模型也會導致模型的計算結果出現不穩(wěn)定情況，因此有必要對擬合出的Y參數進行無源優(yōu)化。

無源性是指一個二端口網絡無論在什么端口條件下均不對外產出能量。假設導納參數矩陣為Y(s)，則電流電壓有如式(4)的關系。

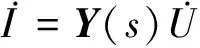
(4)

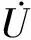
將矩陣Y(s)分解為電導G(s)與導納B(s)之和的形式，則端口網絡吸收的有功功率為

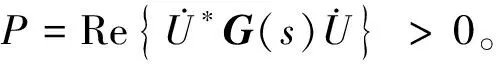
該CVT優(yōu)化前后的導納參數特征根如圖8所示，可見部分小于0的特征值被優(yōu)化為正值，從而保證了端口的無源。

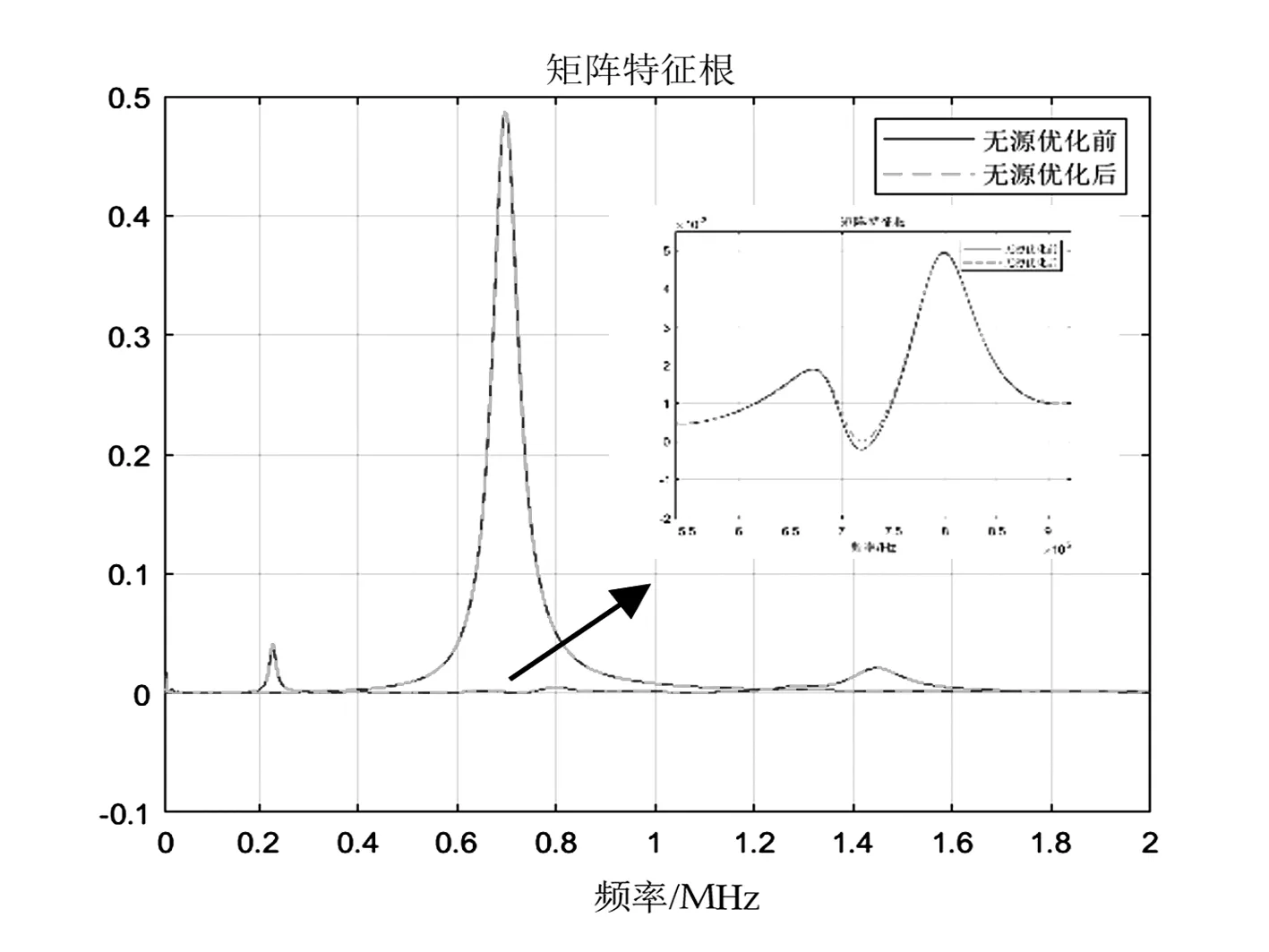
圖8 對導納參數的無源優(yōu)化

2.3 模型的電路實現

基于上一節(jié)獲得的無源優(yōu)化后的二端口Y參數的有理表達式，可用式(6)計算如圖2所示的π型電路中每個子模塊的單端口Y參數有理表達式。

在獲取3個子模塊的單端口Y參數有理表達式后，根據福斯特II型電路綜合理論進行等效電路構建。具體地，每個子模塊的表達式可以化為式(7)所示的福斯特部分分式和表達式[10]。

(7)

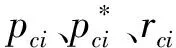
圖9 常數項等效電路

對于實數極點項，可綜合表示為如圖10所示的RL支路，其值如式(8)所示。

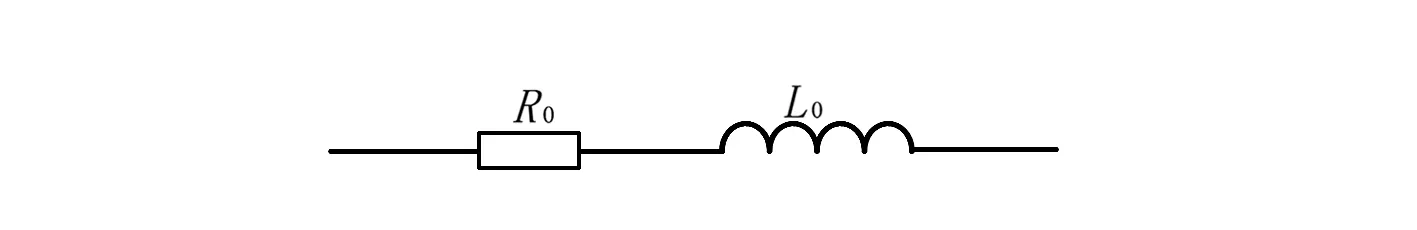
圖10 實數極點項等效電路

對于復共軛極點項，可綜合表示為如圖11所示的RLCG串并聯支路。

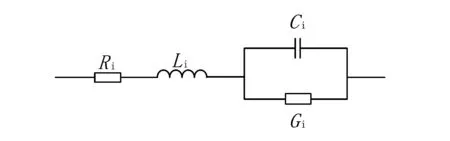
圖11 復共軛極點項等效電路

圖中各元件的值如式(9)所示。

將上述各個電路并聯即可形成子模塊的等效電路。則整個π型電路如圖12所示，模型即建立完成。

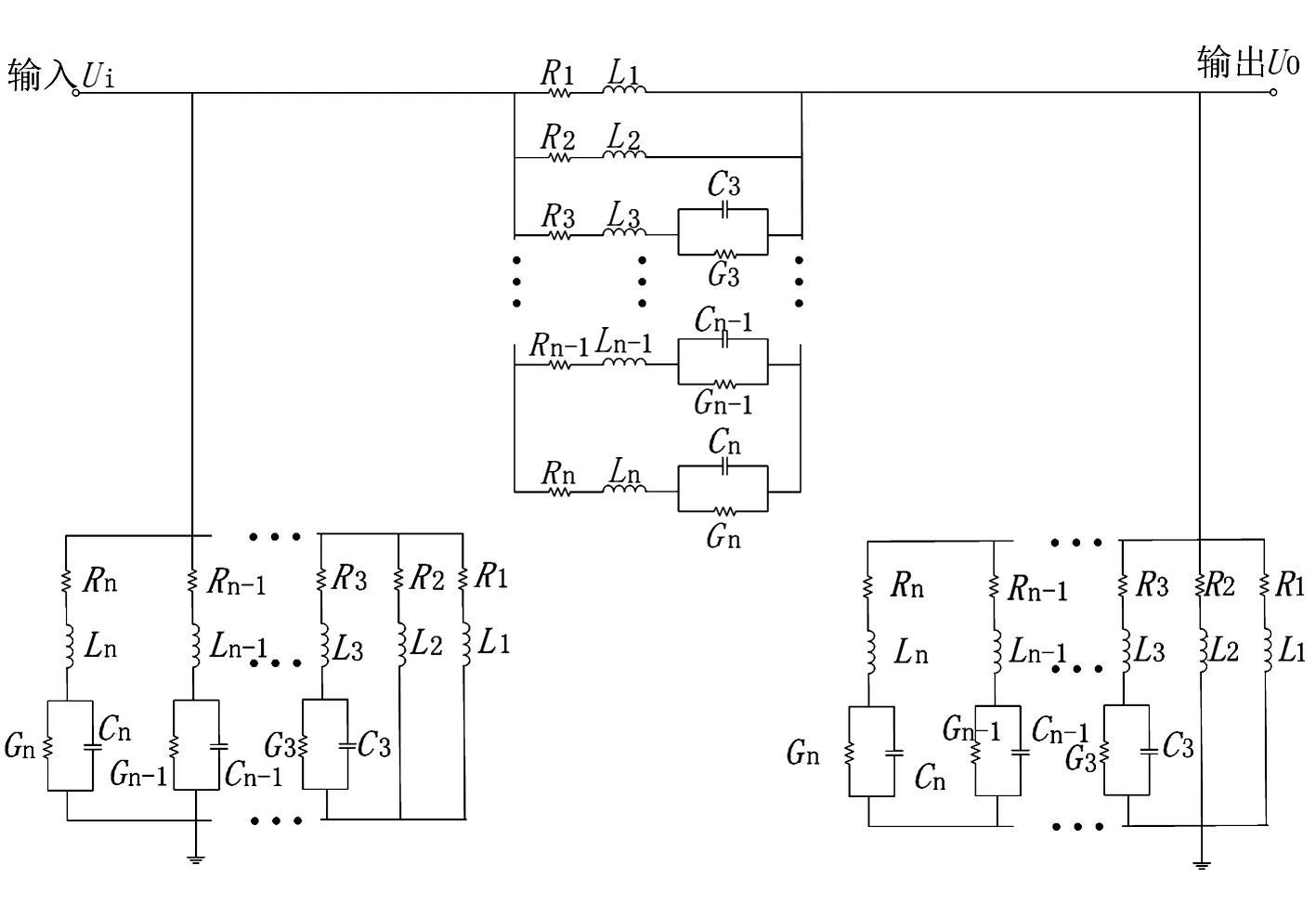
圖12 電路綜合后的黑盒模型

2.4 模型的計算與驗證

為了證實模型的正確性，在測得CVT輸入雷電沖擊波形Uin的情況下通過電路綜合后的黑盒模型計算得到CVT二次側輸出Uout并與實測值對比。

針對圖12中的儲能元件，采用貝杰龍法對其進行處理[11]。電感和電容可分別將其等值電路表示為如圖13所示的形式，圖中的IL(t-Δt)和IC(t-Δt)是電感和電容的歷史電流值。

圖13 電感、電容等值電路

在S參數的測量完成后，不改變CVT的任何配置，對其進行雷電沖擊實驗。雷電沖擊實驗采用實驗用雷電沖擊發(fā)生器對CVT輸入200 kV的標準雷電沖擊波。

首先，將CVT的所有n端良好接地，所有二次側端口均開路。將標準雷電沖擊發(fā)生器的輸出端與CVT高壓輸入端口相連，CVT二次側端口1a—1n通過1000∶1的衰減器后接入示波器。雷電高壓波形通過與CVT并聯的129 700∶1的標準阻尼式電容分壓器輸入示波器。 CVT輸入的高壓雷電波形如圖14所示，實際峰值約為209 kV。

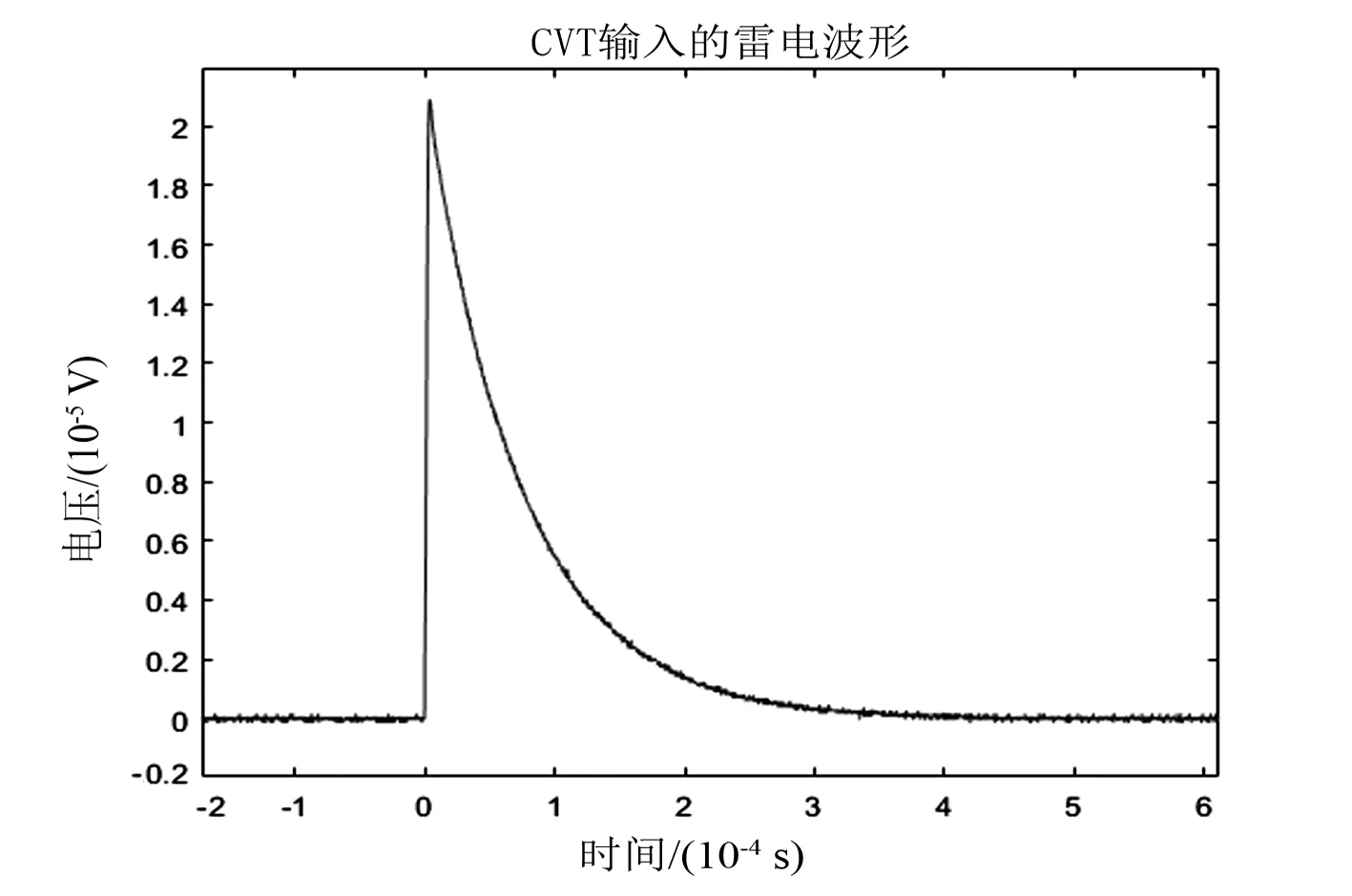
圖14 高壓標準雷電波形

將測得的高壓標準雷電波形帶入所述的支路電流法電路矩陣中，計算得到各時刻CVT二端口輸出情況，與測量的二次側波形進行對比，如圖15所示。

由圖15可看出，計算得到的波形和實驗測得的CVT輸出波形基本一致。

3 結 語

上面利用二端口散射參數、黑盒模型構建了π型CVT黑盒模型，利用矢量匹配法、宏觀無源化和福斯特II型等效電路建立了π型等值電路的CVT模型。為了驗證該模型是否能夠在寬頻暫態(tài)電壓的條件下表征CVT的端口特性，通過網絡分析儀測量CVT的S參數，得到π型等值電路的CVT模型的各個元件參數后，對CVT進行雷電過電壓試驗，在已知CVT高壓輸入雷電波形的情況下利用支路電流法列寫方程，計算得到CVT二端口的輸出波形。最終比較計算波形和測量得到的波形，二者近似相同，驗證了所建立的CVT寬頻暫態(tài)模型的正確性。