基于響應面算法的車載電機成本優化設計
靳 冶,皇甫倩
(1.上海大學 機電工程與自動化學院,上海 200072; 2.中國電子科技集團公司第三十二研究所,上海 201808)
0 引 言
釹鐵硼是構成永磁同步電機原材料成本的主要部分之一,其次是線圈和沖片等材料。根據統計,依賴昂貴稀土材料的磁鋼約占整個車用驅動電機總成本的20%~30%[1]。隨著原材料成本的持續上漲,物料清單的成本越來越高,這和新能源汽車持續降低成本以實現產業化普及的目標背道而馳。因此,車載永磁同步電機的降本設計成為車載電機企業共同研究的熱點。
近年來,持續提高電機功率密度和扭矩密度一度成為電機行業深入研究的重點領域,并出現了眾多優化方法以實現電機性能的提升。但隨著行業的發展,相同車型對驅動電機的需求是類似的。因此利用優化算法,在保證性能指標相近的情況下盡量減少材料的用量,以實現成本的降低。
響應面模型(RSM)是應用于工程和化工領域的一種常見算法,近年來也開始被用于電機的設計優化。當目標函數的自變量較少時,利用響應面法可較快地找到最優解,減少了電機設計對工程師經驗的依賴,并縮短了開發周期,降低了企業研發成本和風險。
在滿足電機輸出性能需求的同時,優化設計磁鋼外形及其用量,能夠降低永磁電機總的材料用量[2]。因此,本文著重優化磁鋼、硅鋼等占電機成本比例較高的材料用量,以降低電機的總材料成本。
根據電動汽車對轉矩和效率的要求,選擇轉矩脈動峰峰值Trip、最大平均轉Tavg,以及較高的運行效率η為優化目標,希望在降低電機磁鋼、硅鋼用量,減少材料成本的同時,保證電機最大平均轉矩、轉矩脈動及效率仍然符合車輛對電機性能的需求。
1 選擇優化參數
轉子中永磁體形狀和布置位置能夠影響電機交軸電感、直軸電感以及磁密的分布,從而影響電機輸出性能和成本[3]。永磁體形狀如圖1所示。

圖1 電機磁極形狀示意圖
本文基于某A00級微型電動汽車原有的需求進行設計。車輛對電機有具體的安裝尺寸要求,因此本文不改變定子外徑、電機長度和單邊氣隙。選用如圖1所示的定轉子內外徑之比α,永磁體槽中心線底部距轉子內圓距離O2、磁鋼厚度h、磁鋼長度W(圖1中的WPM1+WPM2)4個決定永磁體排布的轉子結構變量作為優化參數和自變量,將響應值設置為電機的磁鋼用量。通過自變量的改變能夠求得響應面的最佳情況:
y=f(x1,x2,x3,…,xk)+ε
(1)
式中:y為響應值;x為自變量;k為自變量個數;ε為誤差。自變量與響應值之間關系十分復雜,通常難以找到最優值,因此可以通過響應面模型來近似代替實際函數關系。選取的二階響應面模型[4]:
(2)
式中:β0,βi,βii,βij為回歸系數;ε為誤差;k為自變量個數。
為了方便計算,在求解最優回歸系數時,需將自變量的值進行轉換,將所選取的最小值設為-1,最高值設為1,中間值設為0。真實值和轉換值的關系:
(3)
式中:xinorm為代碼值;xi為自變量取值。
根據不同的回歸系數,由式(2)得到的響應變量y的擬合值是不同的。為了得到擬合程度最好的響應面模型,需要找到合適的回歸系數,使得響應變量y的擬合值和實際測得值的離差平方和Q(β)最小:
(4)
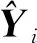
運用最小二乘法,可以求得離差平方和Q(β)最小時的回歸系數矩陣β[5],從而得到響應面的擬合回歸方程:

(5)
在得到擬合方程后,還要用方差分析法來對該方程進行顯著性檢驗,判定擬合方程的精確度。
2 建立響應面模型
響應面設計通常用 CCD(中心復合設計)和Box-Behnken兩種擬合曲面的方法[6]。本文中自變量的個數較少,只有定轉子內外徑之比α,永磁體槽中心線底部距轉子內圓距離O2、磁鋼厚度h,磁鋼長度W這4個。因此,借助Design-Expert軟件,并選擇Box-Behnken作為擬合方法,做4因素3水平的試驗設計。通過Design-Expert軟件求出29個樣本點,再通過motorCAD軟件創建有限元模型,計算每個實驗點的磁鋼用量,硅鋼片用量、銅的用量,并將總的材料成本計為實際的響應值。定轉子內外徑之比α、槽中心線底部距轉子內圓距離O2、磁鋼厚度h以及磁鋼長度W分別取:
0.6≤α≤0.7
21 mm≤O2≤23 mm
5 mm≤h≤6 mm
11 mm≤W≤13 mm
實際材料價格是不斷變化的。參照市場上各種材料的價格,本文使用以下成本計算值進行計算仿真:釹鐵硼700元/kg;銅線80元/kg;沖片10元/kg。

表1 4因素3水平參數列表
圖2是2因素間對總的材料成本影響的3 D響應面圖。圖2是對表2的數據做多項擬合回歸生成的。
并獲得總的材料成本(y) 對定轉子內外徑之比α、永磁體槽中心線底部距轉子內圓距離O2、磁鋼厚度h,磁鋼長度W的二次多項回歸方程:
y=6.592+0.292 5x1+1.168 33x2+
0.305x3+0.589 17x4- 0.065x1x2-
0.025x1x3-0.177 5x1x4+0.217 5x2x3+
(6)
得到成本隨自變量變化的擬合方程后,需要對該方程進行方差分析,驗證方程是否能否合理地描述所選參數和材料成本間的關系。根據總的生產成本擬合出方程的參數,求得模型的判定系數如表3所示。

表2 設計試驗點磁鋼用量計算值

表3 響應面法生產成本分析結果
表3中,R2為總判定系數,Adj-R2是R2的平方值,這兩個判定系數越接近1,代表擬合程度越高,本文中R2=0.962和Adj-R2=0.920 1,非常接近1,表示曲面擬合度越好。AdeqPrecisior為信噪比,取值范圍必須>4,本文模型中AdeqPrecisior=5.843,在合理取值范圍。
3 基于遺傳算法的成本優化
在求得個體適應度后,還需通過遺傳算法得到最大適應度個體[7],流程如圖3所示。

圖2 材料成本和各因素的關系
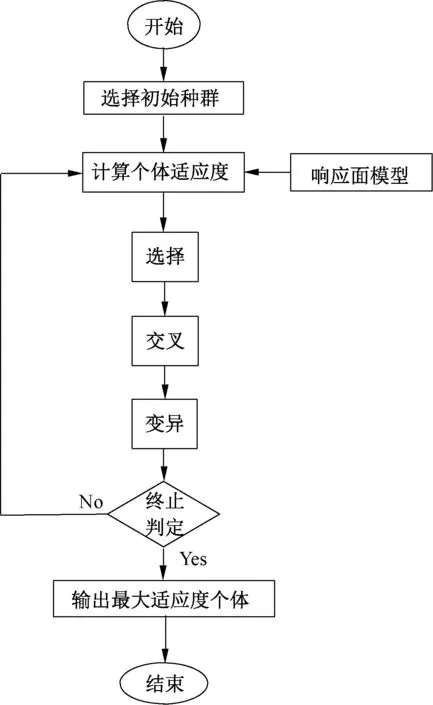
圖3 算法流程圖
在材料成本優化過程中,要保證電機仍然能夠滿足設計參數指標的要求。例如,在本文面向的車型中,電機的峰值效率≥93%,高效區≥85%占55%以上。選取上文所述的4個設計參數作為優化變量,以材料成本最小化為目標進行優化,數學表達式如下:
(8)
式中:Pn為電機的額定輸出功率;Tripple為電機的轉矩脈動;ηn為額定點效率。
圖4 為優化過程。由圖4可知,經過約60代的優化,目標函數y趨于收斂。
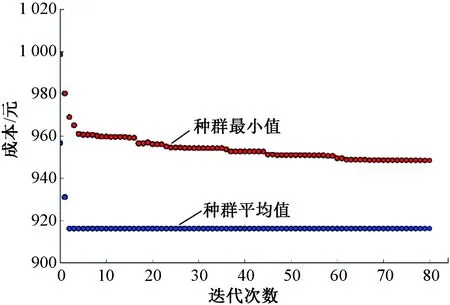
圖4 目標函數優化迭代過程
表4給出了電機總的材料成本優化結果。可以看出,當定轉子內外徑之比α=0.62,永磁體槽中心線底部距轉子內圓距離O2=17.5 mm,磁鋼厚度h=6.1 mm,磁鋼長度W=13.4 mm時,電機總成本從原先的980元降低為948元,有明顯優化效果。

表4 材料成本優化結果對比
優化前后的磁極形狀對比如圖5所示。
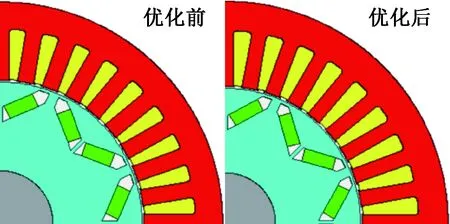
圖5 優化前后的電磁方案
4 有限元驗證
在經過上文的優化后,再利用有限元方法對比電機初始方案及優化后的輸出轉矩,驗證電機的性能仍保持基本不變,并仍滿足設計要求。如圖6所示,優化后的輸出轉矩平均值結果為29.4 N·m,原方案為30.1 N·m,基本相同。轉矩脈動Tripple=3.4%,優化前為3.1%,轉矩脈動幅值有所增大,但仍在設計指標要求的5%以內,并且變化不大。
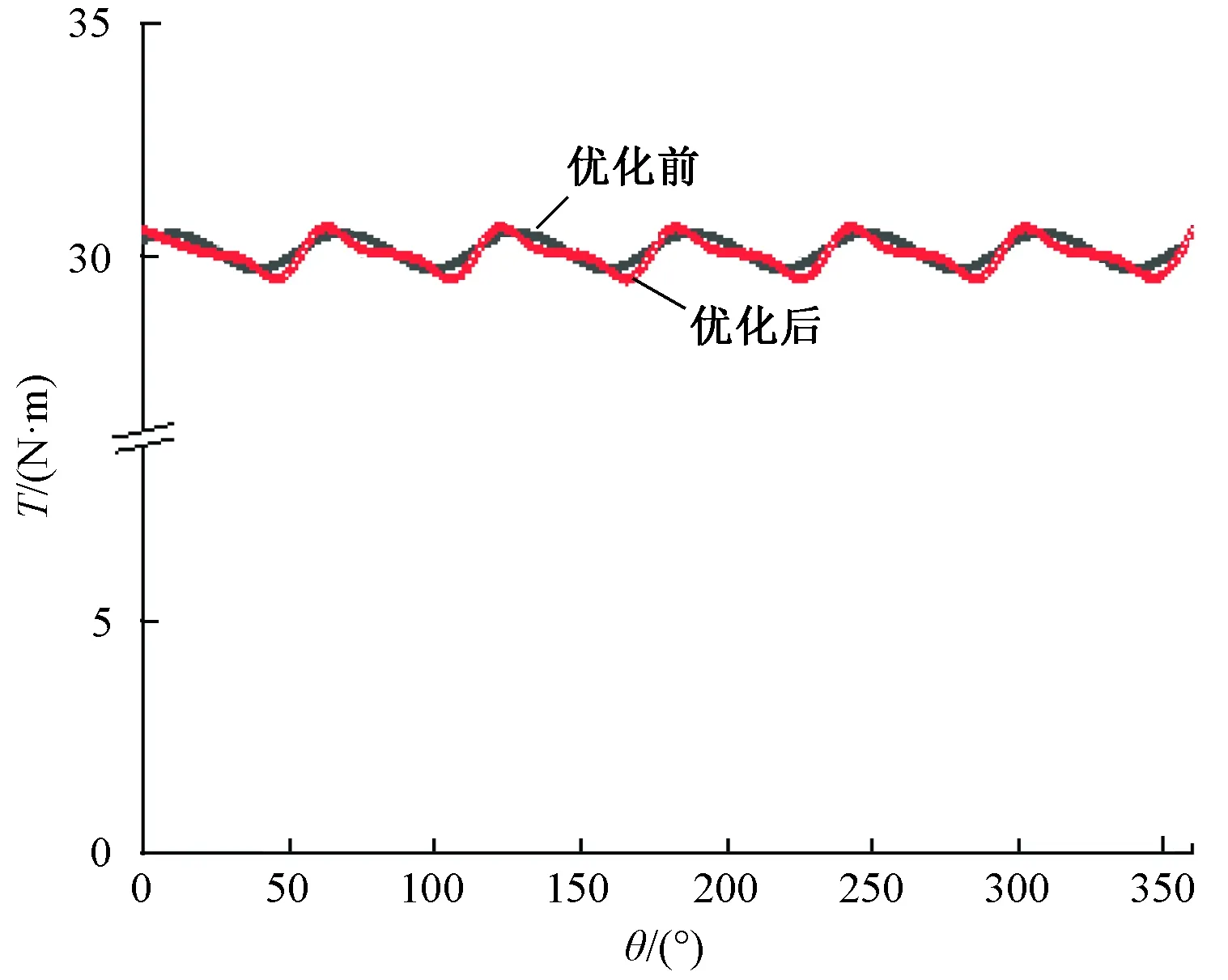
圖6 優化前后輸出轉矩對比圖
圖7為優化前后的效率Map對比圖,其中包含了NEDC工況點。可以看出,優化前后最大輸出轉矩幅值大小基本不變,但是優化后效率最大值覆蓋面積略微降低。由于Lq/Ld的幅值增大,優化后的電機弱磁能力有所提高。

圖7 優化前后效率Map對比
從圖7可以看到,優化后的最高效率為95%,效率在85%以上的面積占比為87.61%,滿足了設計指標。但優化后的效率略有降低,尤其效率為95%以上的高效率區有所差異。優化后的95%效率區域縮小了。由于用于車輛驅動時,綜合效率是由工況決定的,所以比較綜合工況下的效率才有實際意義。通過Motor-CAD Lab模塊結合NEDC工況的仿真,優化前后的效率如圖8所示。
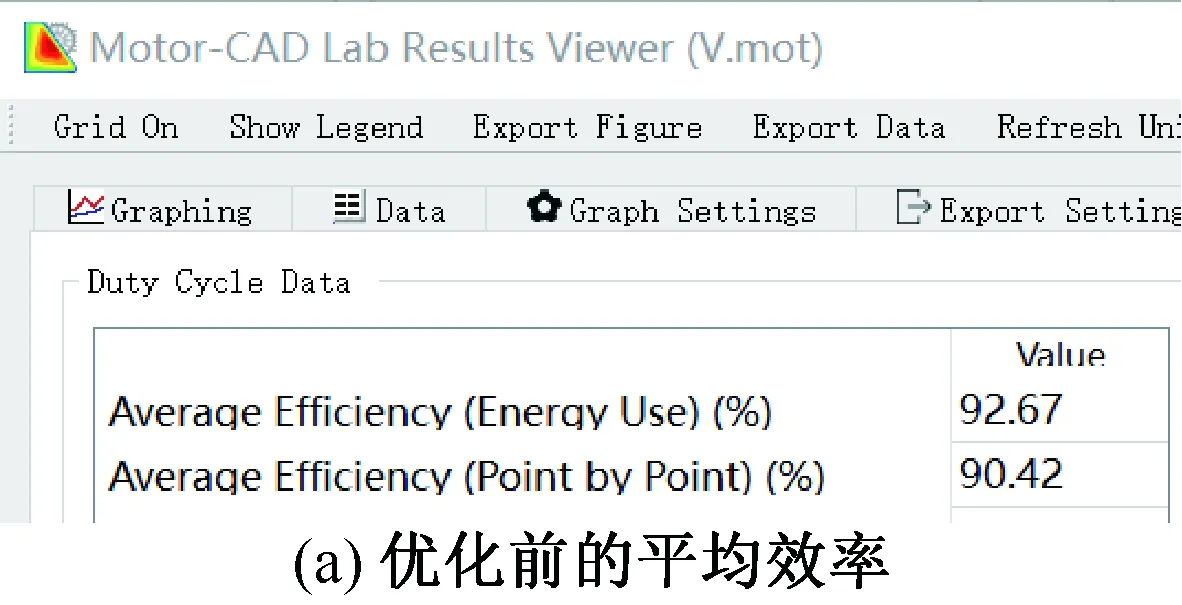
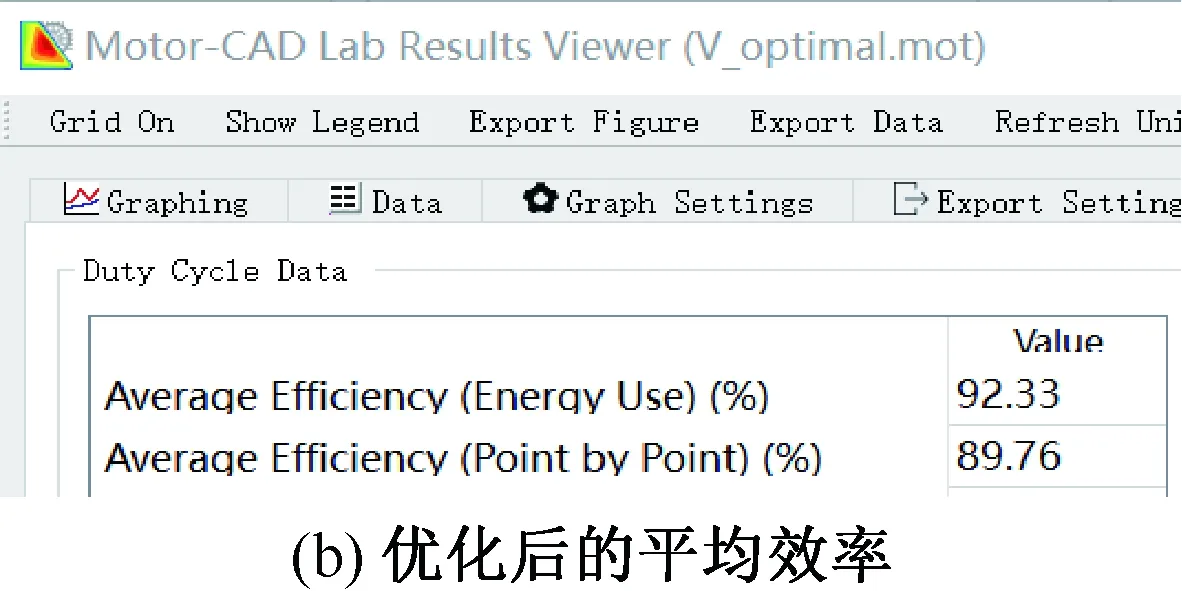
圖8 優化前后的效率
對比顯示,在NEDC工況下,優化前后的效率并無顯著差別。達到了保持性能參數基本不變的前提下節省材料的目的。
5 結 語
圖9是實際電機的沖片圖和臺架測試照片。
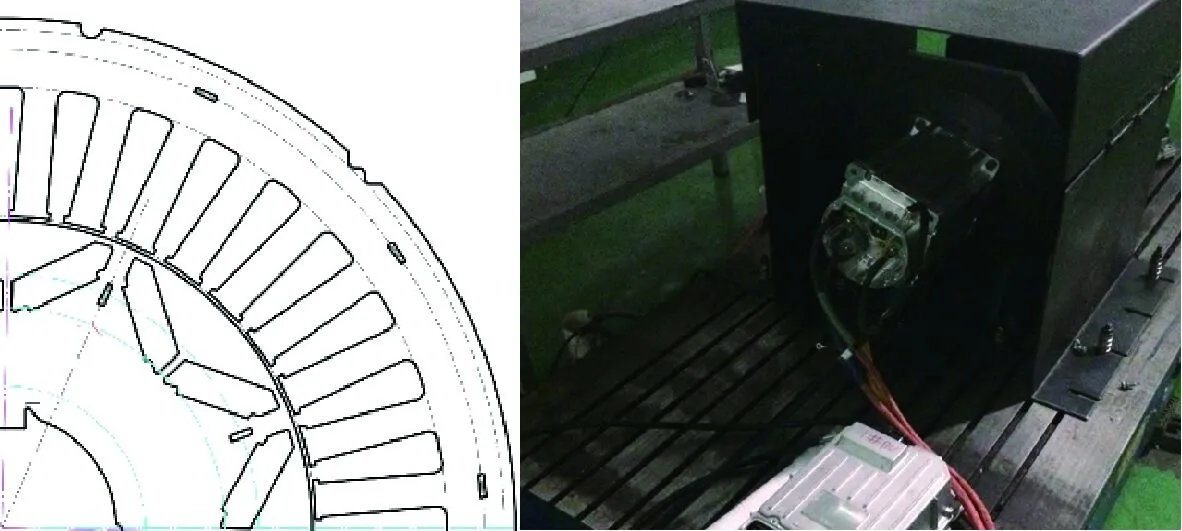
圖9 樣機的電磁方案和試驗臺架照片
經過實際臺架測試,電機的MAP圖如圖10所示。
綜上所述,采用響應面模型,結合遺傳算法,以材料用量為優化目標,合理選取優化參數,通過多次迭代,實現了在保持電機參數性能基本不變的前提下,減少材料用量、降低成本的目的。
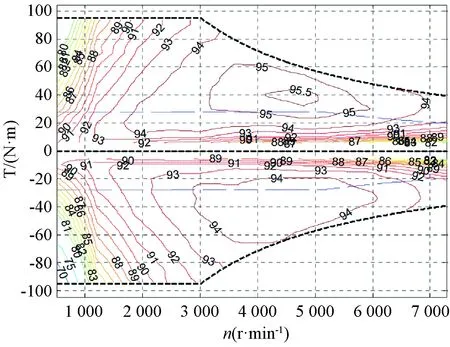
圖10 樣機的實測MAP圖

