大功率直驅風力發電機軸承應力場有限元計算

王騰飛，李海江

(中車株洲電機有限公司，株洲 412000)

0 引 言

風能是重要的清潔能源，大規模風能開發與利用是我國重要的能源戰略。傳統的非直驅風力發電機的傳動鏈由葉片、輪轂、主軸、齒輪箱和發電機組成，其主軸承一般位于輪轂內。齒輪箱故障導致風電裝備發生安全事故,增加維護成本，嚴重影響風力發電機的安全性和經濟型[1]。近年來，大功率(目前已高達12 MW)直驅風力發電機組已成為我國風電新增容量的主力機型之一[2]。圖1為一種典型的直驅風力發電機組傳動鏈示意圖，發電機組由風輪(葉片+輪轂)直接驅動發電機，發電機轉軸(主軸)一般采用空心軸。圖1中的發電機軸承即為直驅風力發電機組主軸承，為兩單列圓錐滾子軸承。直驅風力發電機組傳動鏈中沒有齒輪箱，從根本上解決了齒輪箱的安全、維護等重大問題，但同時，強陣風直接沖擊作用在主軸承上，對主軸承的性能提出了極高要求。準確分析主軸承的受力狀態，從而合理設計和配置主軸承，對于直驅風力發電機組安全運行至關重要。

圖1 一種典型的直驅風力發電機組傳動鏈示意圖

風力發電機軸系結構復雜，采用經典力學理論計算難以得到準確結果[3]。隨著計算機技術的不斷發展，有限元分析方法得到了越來越廣泛的應用[4-8]，但是大型風電軸承包含幾百個非線性接觸對，若采用全實體建模網格數量龐大，對計算硬件資源要求極高，耗時耗力且不易收斂。文獻[6]基于ROMAX建立了直驅風機軸系模型，得到了游隙與載荷分布的關系，但缺少對軸承接觸應力的理論分析。文獻[7]采用GAP間隙單元模擬軸承滾子，得到了軸承載荷分布，但缺少對滾子/滾道接觸剛度的分析，且仿真結果缺少驗證。文獻[8]基于非線性彈簧建立了三排圓柱滾子組合轉盤軸承計算模型，分析了轉盤軸承在外力作用下的內部接觸載荷分布和整體變形情況，但采用有限元方法計算滾子/滾道的非線性接觸剛度曲線效率不高，同時仿真結果缺少驗證。

本文以兩個單列圓錐滾子軸承配置的大功率直驅風力發電機軸系為研究對象，基于有限長非赫茲接觸理論計算了圓錐滾子軸承的滾子/滾道接觸的剛度曲線，采用非線性彈簧單元模擬滾子/滾道接觸，構建了直驅風力發電機軸系有限元模型，得到了極限工況下的軸承載荷分布，并利用接觸分析程序計算了軸承應力，在保證計算精度的同時，較大地提升了計算效率，為產品設計開發提供了充分的參考依據。

1 直驅風力發電機有限元模型

1.1 軸承有限元模型

軸承有限元模型如圖2所示。軸承內外圈采用實體單元建模，模型中簡化了倒角等局部細節。內外圈之間采用彈簧單元模擬滾子接觸。圓錐滾子軸承的滾子/滾道接觸為線接觸形式，理論上代替滾子的彈簧數量越多，計算結果越精確，但彈簧數量的增加會導致計算效率下降，且對硬件資源需求也更高。為了有效模擬軸承變形，經過測試可以沿著滾子母線方向，以5根非線性彈簧單元替代滾子/滾道接觸，這樣既能提高計算效率，又可以保證準確性。

圖2 軸承有限元模型

有限元彈簧單元模擬滾子就是用彈簧單元的剛度代替滾子/滾道的接觸剛度，因此要構建軸承有限元模型必須首先計算得到滾子/滾道的接觸剛度。

滾子/滾道接觸并非無限長接觸，已經超出赫茲接觸理論范圍。根據彈性接觸理論，兩彈性接觸體間的接觸問題的基本方程[5-9]：

(1)

(2)

式中：z為兩接觸體初始間距；Q為接觸載荷；δ為彈性趨近量；Ω為接觸區域；p為接觸應力；E′為當量彈性模量：

(3)

針對滾子/滾道接觸問題，最直接的數值解法是將接觸區域劃分為m×n個矩形單元，然后將積分方程離散成(m×n+1)階線性方程組，但是該方程組求解效率不高。作為替代，可以采用“切片法”進行求解上述基本方程：將接觸區域Ω沿滾子母線方向劃分為m個單元，假設單元格接觸應力poj沿滾子母線方向均勻分布，沿滾子截面方向呈赫茲分布，如圖3所示。

圖3 接觸應力示意圖

(4)

由此將上述接觸問題基本方程離散轉換為(m+1)階線性方程組：

(5)

(6)

運用數值計算方法求解上述方程組流程圖如圖4所示。

圖4 數值計算流程

將上述步驟利用VB編制成接觸分析數值計算程序，即可快速求解得到軸承的滾子/滾道接觸剛度曲線及應力。

軸承結構參數如表1所示。將其代入接觸分析數值計算程序，得到如圖5所示的彈簧單元剛度曲線。

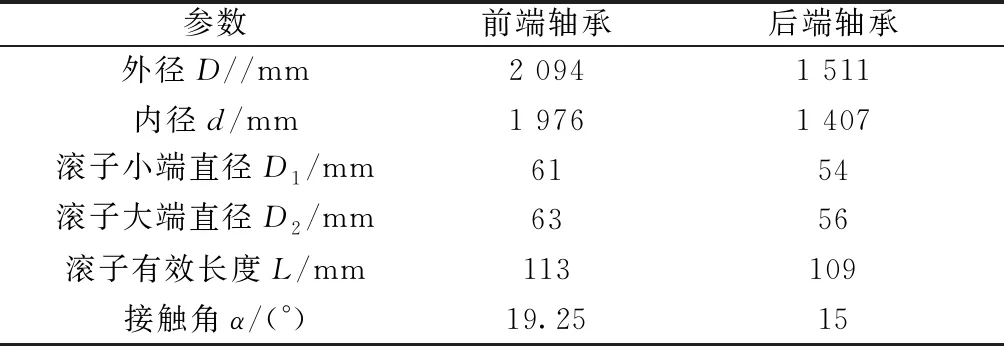
表1 軸承基本參數

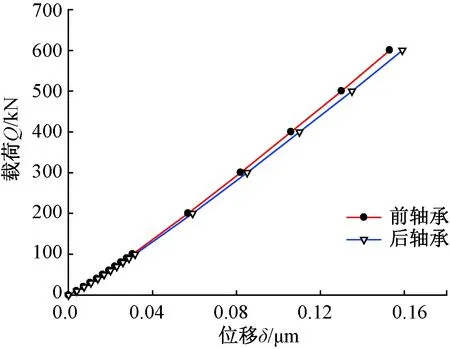
圖5 滾子剛度曲線

1.2 軸系有限元模型

為了便于前處理，提高計算效率，對軸系模型進行了適當簡化：省去了螺栓等不重要零部件，忽略了動定軸局部倒角等細節。

輪轂通過螺栓與轉軸連接，并在風力作用下帶動發電機旋轉，有限元模型中用輪轂中心點代替輪轂實體，等效風載荷作用于輪轂中心。定軸與基座相連，分析時約束與基座連接的定軸端面，軸承與軸之間采用摩擦接觸，摩擦系數設置為0.1。有限元模型如圖6所示。

圖6 軸系有限元模型

2 模型驗證及實例

為了驗證上述有限元模型的正確性，在工廠內實測直驅風力發電機主軸承的摩擦力矩，并與有限元模型的計算值進行對比。圖7是軸承摩擦力矩測量示意圖。發電機豎直安置于平臺上，尼龍吊帶一端固定在發電機定軸上，另一端固定在叉車上，叉車拖動定軸旋轉，測量拉力值，換算得到旋轉力矩。圖8是實驗現場圖。

圖7 摩擦力矩測量示意圖

圖8 實驗現場圖

在端蓋預緊后，利用叉車對裝配完成的6臺風力發電機進行摩擦力矩測量，每臺測量10次，取平均值。測量結果如表2所示。

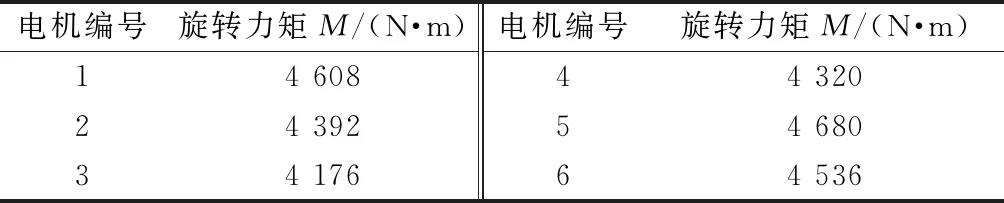
表2 摩擦力矩測量值

從表2可以看出，摩擦力矩測量值有波動，這是由于不同電機軸承的潤滑狀態、加工及裝配精度等差異而導致的結果。

下面對該模型進行摩擦力矩分析，采用如下經驗公式進行計算[10]：

(7)

式中：μ為摩擦系數，d為摩擦力作用內徑，P為軸承當量動負荷。

經計算得到實驗條件下的軸承等效靜載荷及當量動載荷，如表3所示，其中Fa為軸向力，Fr為徑向力。

表3 軸承載荷計算結果

摩擦系數受運行狀態、潤滑情況、受載大小等因素影響較大，無法精確測定。文獻[11]給出摩擦系數取值范圍為μ=0.001 8～0.002 8，將其代入摩擦力矩計算公式，計算得到前后軸承摩擦力，進而計算總摩擦力矩：

M總=M前+M后=3 817～5 938 N·m

由表2可見，摩擦力矩測量值波動范圍為4 176～4 680 N·m，包含在計算摩擦力矩值3 817～5 938 N·m范圍內，說明該模型是有效的。

在給定表4的極限載荷工況條件下，對該軸系有限元模型進行求解，得到軸承載荷分布，如圖9所示。

從載荷分布圖中可以看出，最大滾子載荷為450 kN，將此載荷代入前述接觸分析數值計算程序對滾子接觸應力進行計算，如圖10所示。結果表明，最大值應力為2 780 MPa，在設計要求范圍內。

表4 極限載荷工況

圖9 軸承滾子載荷分布圖10 滾子最大接觸應力

目前，該方法已成功應用于直驅風力發電機開發設計過程，有效提升了直驅風力發電機正向設計能力。

3 結 語

1) 采用非線性彈簧模擬滾子/滾道接觸，基于無限長非赫茲接觸理論，運用VB語言編制了軸承接觸分析計算程序，得到了圓錐滾子軸承接觸剛度曲線，構建了基于接觸理論的軸承有限元模型，并進一步構建了軸系有限元模型。

2) 通過摩擦力矩測試得到了發電機的摩擦力矩實測值，與仿真計算的摩擦力矩結果對比，表明仿真模型有效。

3) 基于軸系有限元模型得到了極限工況下的軸承載荷分布，并利用軸承接觸分析計算程序得到了最大應力場分布，結果表明，最大接觸應力在設計要求范圍內。