基于鎖相環改進SVPWM同步調制技術的研究
單寶鈺,尹國龍,高宏洋,劉金晶
(中國中車大連電力牽引研發中心有限公司,大連 116022)
0 引 言
永磁同步電機(以下簡稱PMSM)轉子結構由永磁體替代了異步電機的勵磁繞組的結構,降低了高速運行時轉子發熱的問題,并且PMSM具有體積小、效率高、低速轉矩大等優勢,漸漸地被應用在需要高速運行、負載變化大的領域。由于PMSM相比異步電機極數多,當大功率運行時,受功率開關器件溫升限制,需要降低開關頻率,因此高速區運行采用波形對稱的SVPWM同步調制控制策略。但是,傳統SVPWM同步調制策略隨著載波比減小,輸出諧波含量高,無法平滑切換到方波運行,逆變器開關損耗大,導致逆變器發熱嚴重。
文獻[1]介紹了多模式SVPWM同步調制原理和采樣方式,與傳統SVPWM異步調制進行了比較,驗證了方法的合理性和可行性,但該方法調制波為傳統SVPWM調制波形,全速度范圍運行時存在模式間切換,且最終只能切換到9分頻運行,實際PWM脈沖數為9,諧波含量高,逆變器開關損耗大。
文獻[2]采用了多模式調制方法,即SVPWM異步調制—SVPWM同步調制—特定諧波消除PWM—方波調制,實驗驗證了方法的可行性。雖然文中簡化了數學模型和切換方式,但還是存在多模式之間切換時的波形不連續問題,實驗采用電機功率較小,切換過流等問題并未體現,在實際工程應用中電機功率較大,外部供電因素干擾使切換過流問題更加明顯。
文獻[3]采用方法雖也為同步調制方式,但存在多模式轉換,無法實時調節,實際工程化應用時存在動態響應不高,容易引起切換過流的問題。
針對以上問題,本文提出了一種基于鎖相環改進SVPWM同步調制算法,通過在高速區引入簡化單模式連續過調制算法,實現高速區平滑切換至方波,減小輸出諧波含量,減小開關次數,降低開關損耗。由于簡化單模式連續過調制方式無需計算開關角及區分模式轉換,簡化了數學模型和計算過程,減少了程序計算量,提高了算法執行效率[4]。
1 基于鎖相環SVPWM同步調制
1.1 SVPWM同步調制基本原理
SVPWM同步調制算法是在異步調制基礎上,結合同步調制對稱的特點進行了優化,在變頻調速控制時始終保持載波和調制波同步變化,使得PWM脈沖輸出半波奇對稱、四分之一周期偶對稱和三相對稱[5]。
相比SVPWM異步調制算法間隔恒定的采樣方式,SVPWM同步調制算法則采用空間電壓矢量相位差恒定的采樣方式。通過使空間電壓矢量相位三相對稱、電壓波形正負半周對稱、電壓波形在最大值或最小值的軸線對稱,即每個扇區采樣的次數為奇數、采樣矢量關于每個扇區的角平分線對稱,原理如圖1所示[6-7]。
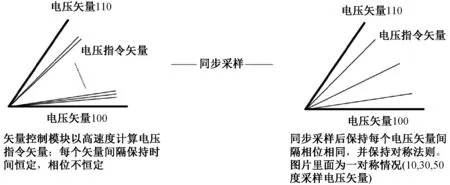
圖1 同步采樣原理示意圖
異步電機空間電壓矢量相位采用開環控制,但PMSM矢量控制時需要定轉子相位絕對保持一致,因此對空間電壓矢量相位進行閉環控制,通過等幅值的坐標變換轉換到指定的對稱角度,原理框圖如圖2所示。
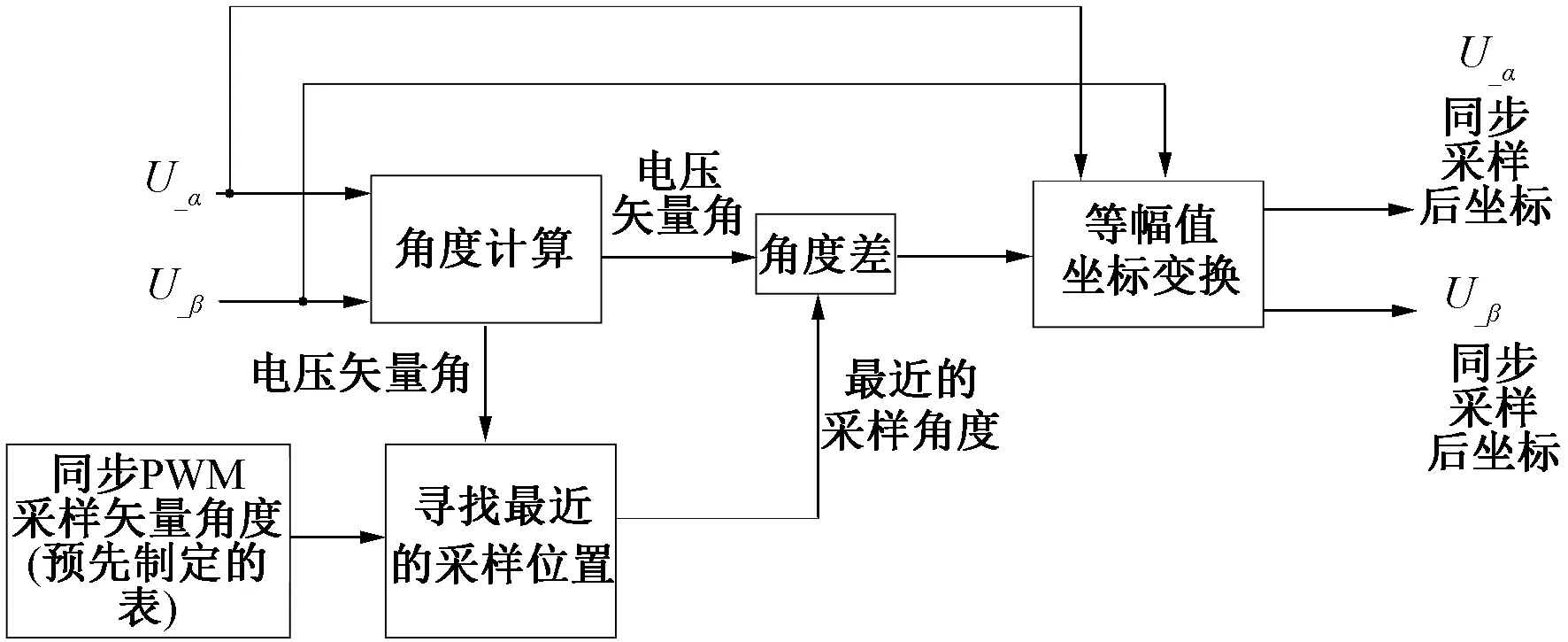
圖2 同步采樣補償原理框圖
以第一扇區為例,根據伏秒平衡原則可知,空間電壓矢量數學模型如下:
(1)
式中:t0為零矢量作用時間;t1為空間電壓矢量作用時間1;t2空間電壓矢量作用時間2;Ts為開關周期;α為空間電壓矢量相位角[8-9]。
1.2 基于鎖相環同步調制策略
PMSM相比于異步電機極對數多,在同樣的轉速范圍內,PMSM的最高頻率比異步電機高,并且由于其定、轉子頻率需要嚴格保持一致,不能出現失步現象,因此其在高速下的脈沖調制方式與異步電機不盡相同。
無論異步電機還是PMSM,當載波比小于15時,為保證線電壓最大限度的對稱,一般都需要使用同步調制策略,使調制波和載波比保持一致。
本文使用鎖相環把電壓相位與載波相位鎖定,即當線電壓相位變化時,通過鎖相環函數PI調節器調節載波周期,使載波以同樣的趨勢改變相位,最終達到兩者相位角度實時保持一致。載波計數周期和PWM中斷頻率關系:
(2)
式中:fPWM為PWM中斷頻率;fsw為開關頻率。
鎖相環的具體實現方式為在每一個中斷函數中,計算合成空間電壓矢量Us與α軸的夾角θ,并把該角度作為反饋值,送入鎖相環調節模塊,用于載波周期值的調整。Us的起始角度可以任意取值,這里Us的起始角度為α軸位置。
鎖相環輸出量用于調節載波周期的大小,即:
(3)

基于鎖相環的同步調制流程圖如圖3所示。
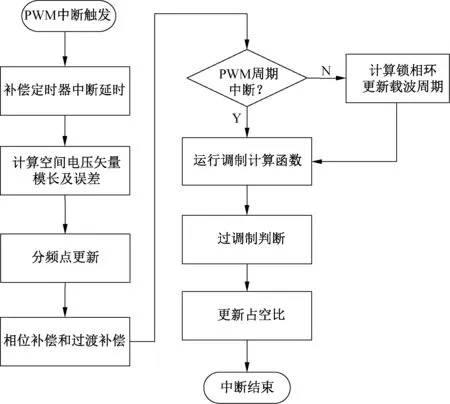
圖3 軟件執行流程圖
以9分頻為例,根據同步調制采樣規則可得算法的調制波和載波波形如圖4所示。
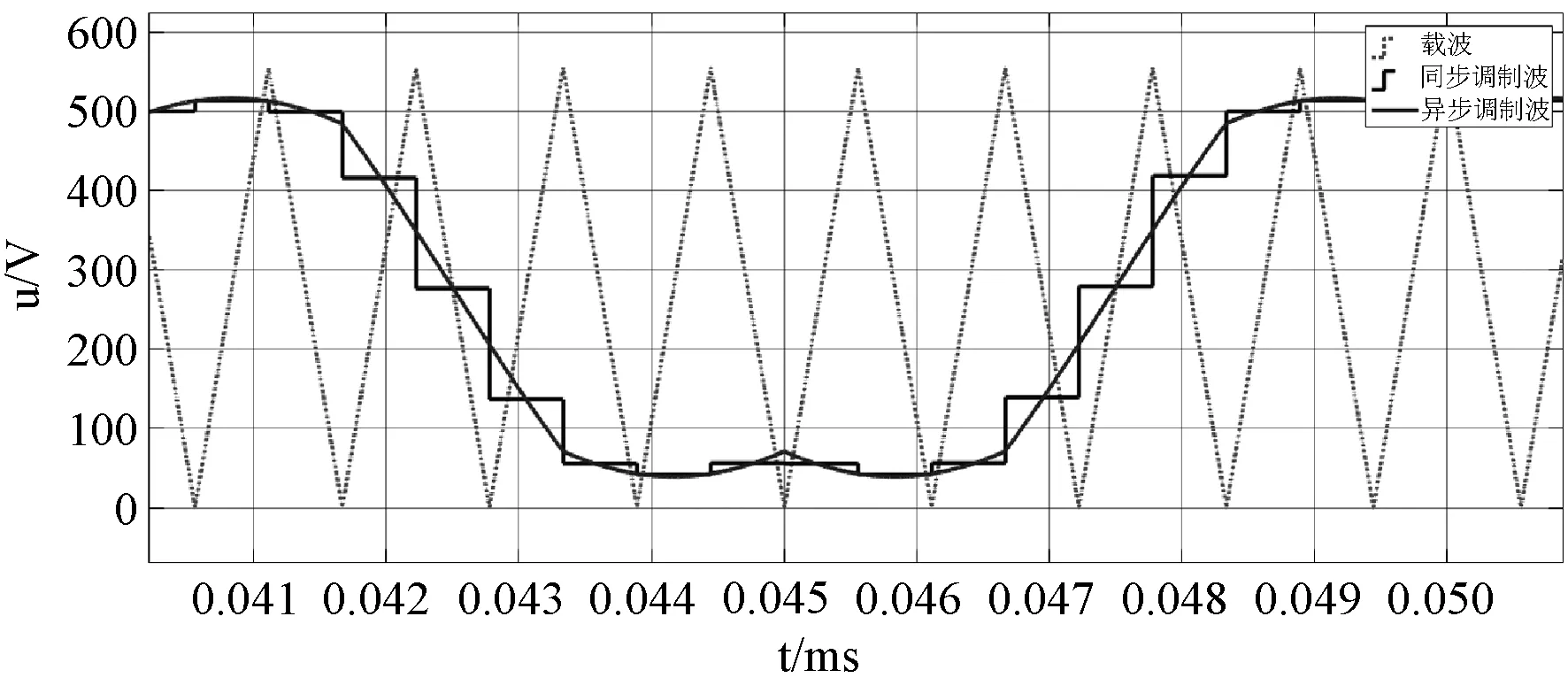
圖4 SVPWM同步算法波形
以上基于鎖相環SVPWM同步調制算法在PMSM矢量控制策略中最后過渡到9分頻,需要進行調制切換到方波調制狀態,為了進一步降低開關頻率,減小逆變器損耗,提高母線電壓利用率,本文通過引入簡化單模式過調制算法,在此基礎上,使逆變器平滑過渡到方波工作狀態[10-11]。
1.3 簡化單模式過調制數學模型
傳統大功率永磁電機牽引控制采用SVPWM異步調制—SVPWM同步調制—方波調制,存在多模式切換,模式之間過渡不平滑,且無法直接過渡到方波運行,運算復雜。本文通過引入簡化單模式過調制算法,簡化了過調制區切換和扇區判斷,減小了算法運算量,提高了算法執行效率。
根據矢量控制算法電壓計算數學模型可得:
(4)
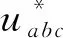
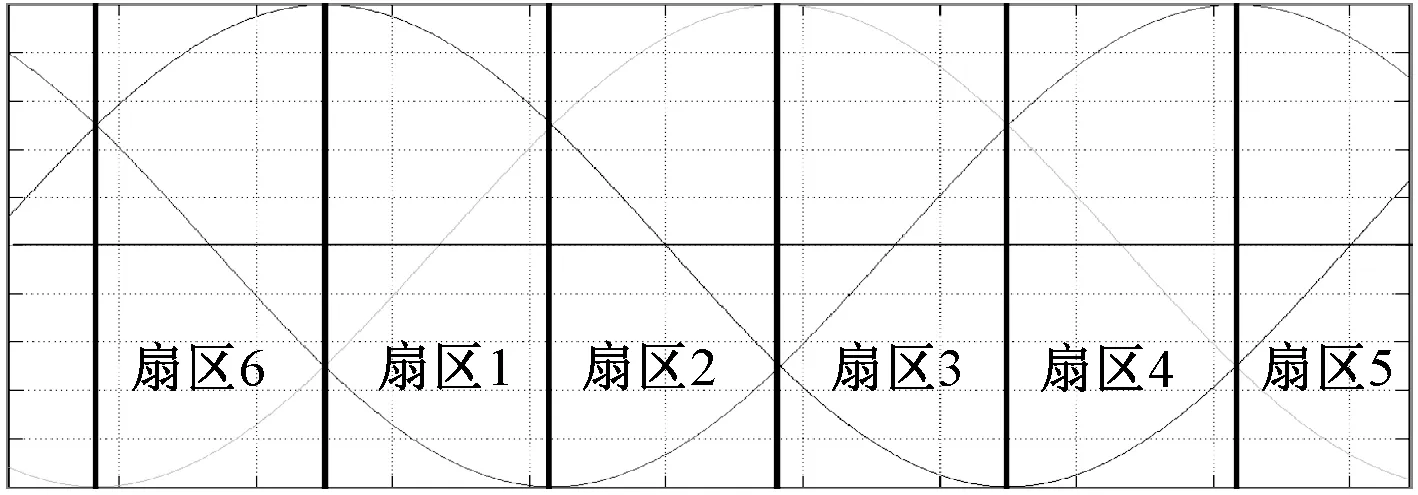
圖5 空間電壓矢量扇區關系
以第一扇區為例,由式(1)可得:
(5)
根據三相電壓相位關系可得空間電壓矢量作用時間[6-7]:
(6)
式中:t0為零矢量作用時間;t1為空間電壓矢量作用時間1;t2空間電壓矢量作用時間2;Ts為開關周期。
(7)
(8)
式中:um為中間簡化算法中間計算變量;t′1,t′2為過調制區空間電壓矢量作用時間;Ta,Tb,Tc分別為三相調制波比較值。
2 改進SVPWM同步調制算法仿真分析
2.1 仿真模型
通過前文數學模型推導,搭建基于鎖相環改進SVPWM同步調制仿真模型,進行算法驗證和諧波含量分析。
如圖6所示,仿真模型包含PMSM、矢量控制算法模型、SVPWM同步過調制算法模型、逆變器電路和檢測電路。
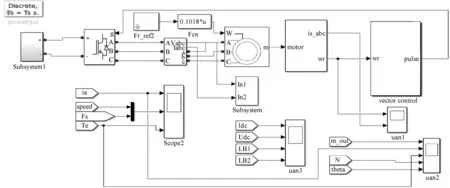
圖6 改進SVPWM同步調制PMSM控制系統
仿真參數如下:
Time0采樣時間為10 μs,Time1采樣時間為1 ms,網壓Uline= 800 V,仿真用電機參數與實驗用電機參數保持一致:Un= 530 V,Pn= 106 kW,fn= 68 Hz,Rs= 0.015 35 Ω,Ld= 0.000 749 1 H,Lq= 0.001 277 5 H,Fm= 0.274 Wb,8極。

圖7 改進SVPWM同步調制作用時間仿真模型
SVPWM同步過調制作用時間仿真模型包含了同步過調制算法和傳統同步調制算法模型,通過模式選擇進行切換。
2.2 分頻波形對比分析
如圖8所示,以9分頻為例,當給定調制系數為0.9時,傳統SVPWM同步調制實際脈沖數為9,此時同步過調制算法未進入過調制區,實際脈沖數也為9。
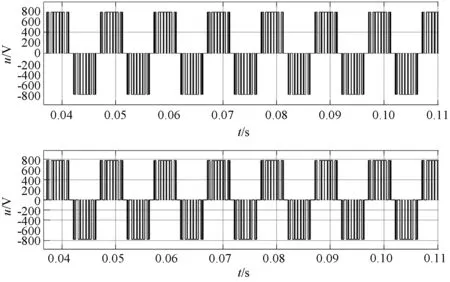
圖8 SVPWM同步調制和同步過調制波形1(調制系數0.9)
如圖9所示,上半部分為同步過調制算法,下半部分為傳統同步調制算法。進一步給定調制系數為1.0時,由于調制系數超過0.906 9時,進入過調制區。傳統同步調制給定為0.9,兩種算法實際脈沖數為9和6。
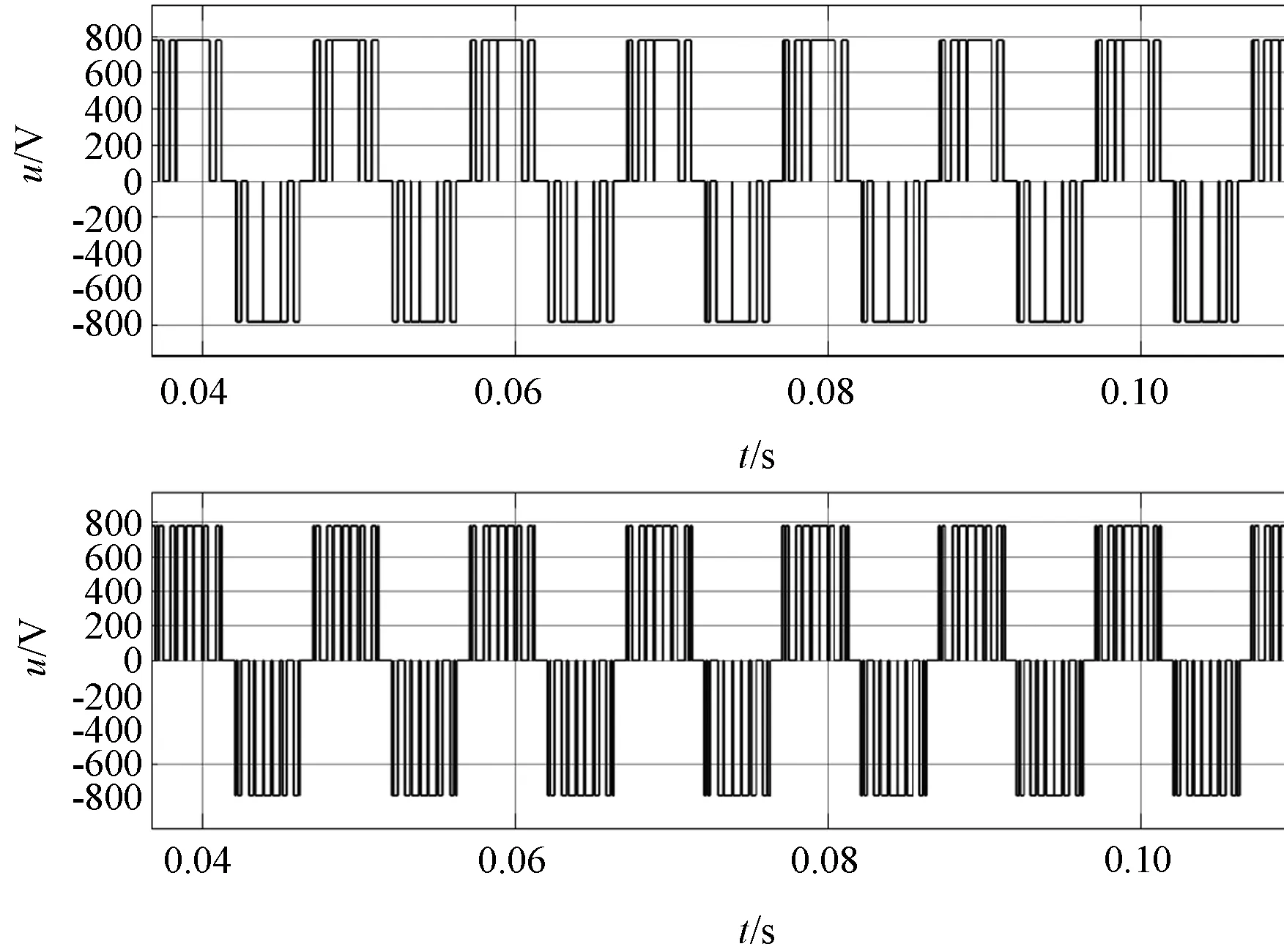
圖9 SVPWM同步調制和同步過調制波形2(調制系數1.0)
如圖10所示,上半部分為同步過調制算法,下半部分為傳統同步調制算法。當調制系數為1.1時,SVPWM同步過調制算法實際脈沖數為3。
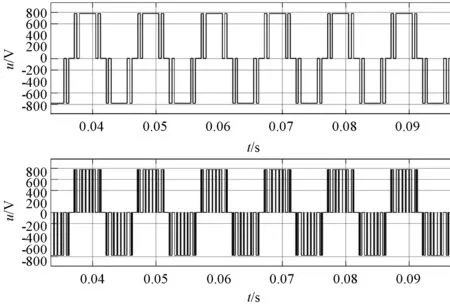
圖10 SVPWM同步調制和同步過調制波形3(調制系數1.1)
如圖11所示,上半部分為同步過調制算法,下半部分為傳統同步調制算法。當調制系數為1.2時,SVPWM同步過調制算法實際脈沖數為1。
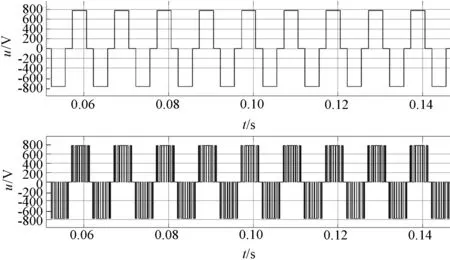
圖11 SVPWM同步調制和同步過調制波形4(調制系數1.2)
通過線電壓輸出對比可知,相比傳統算法,逆變器開關次數降低了66%以上,大幅降低了逆變器開關損耗。當調制系數由1.1調整為1.2時,同步過調制算法下,調制波波形由三脈沖順利過渡到單脈沖的方波模式,進一步降低了開關頻率和開關損耗。
SVPWM同步過調制可平滑過渡至方波運行,且波形連續平滑,下面針對兩種算法輸出諧波含量進行對比分析。
2.3 諧波對比分析
當電機運行在1 500 r/min(100 Hz)和3 000 r/min(200 Hz)時,進行傳統算法和改進算法諧波對比分析,結果如圖12~圖15所示。
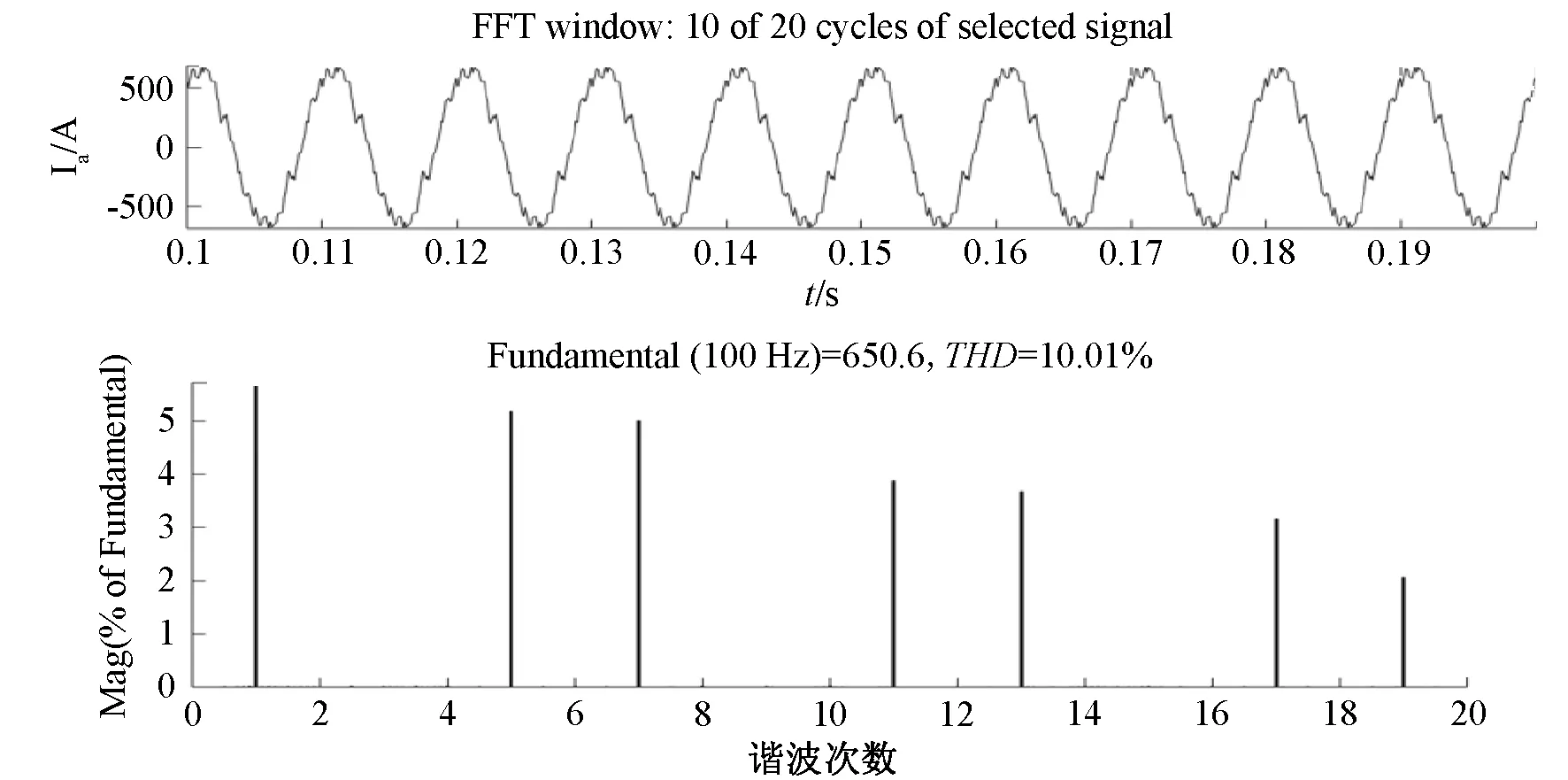
圖12 傳統算法Ia及其諧波含量波形圖(1 500 r/min)
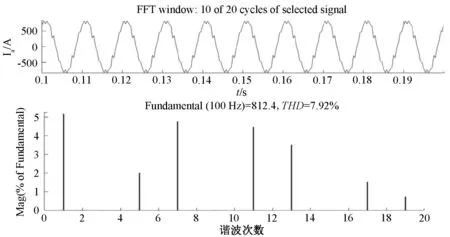
圖13 改進算法Ia及其諧波含量波形圖(1 500 r/min)
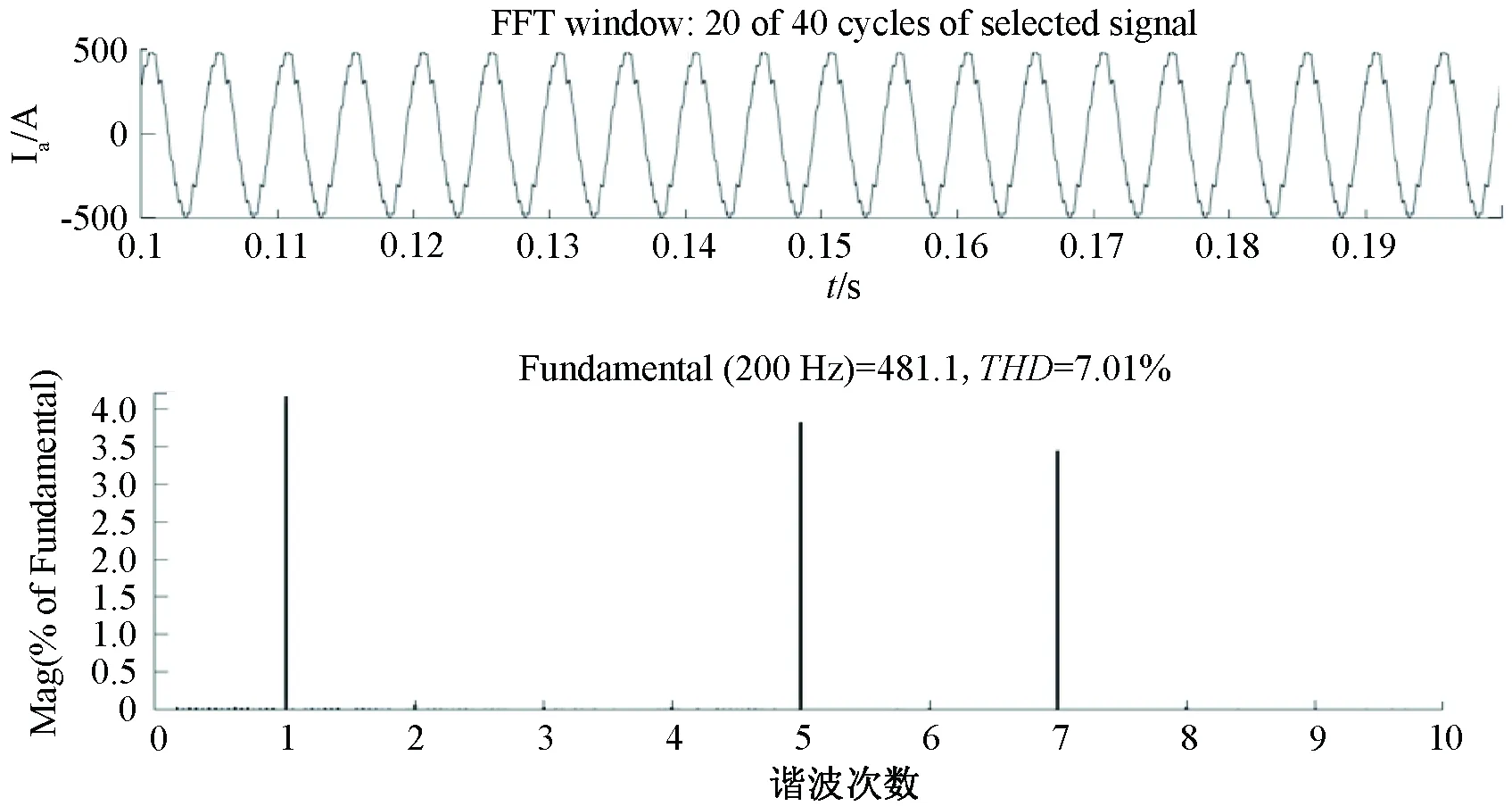
圖14 傳統算法Ia及其諧波含量波形圖(3 000 r/min)
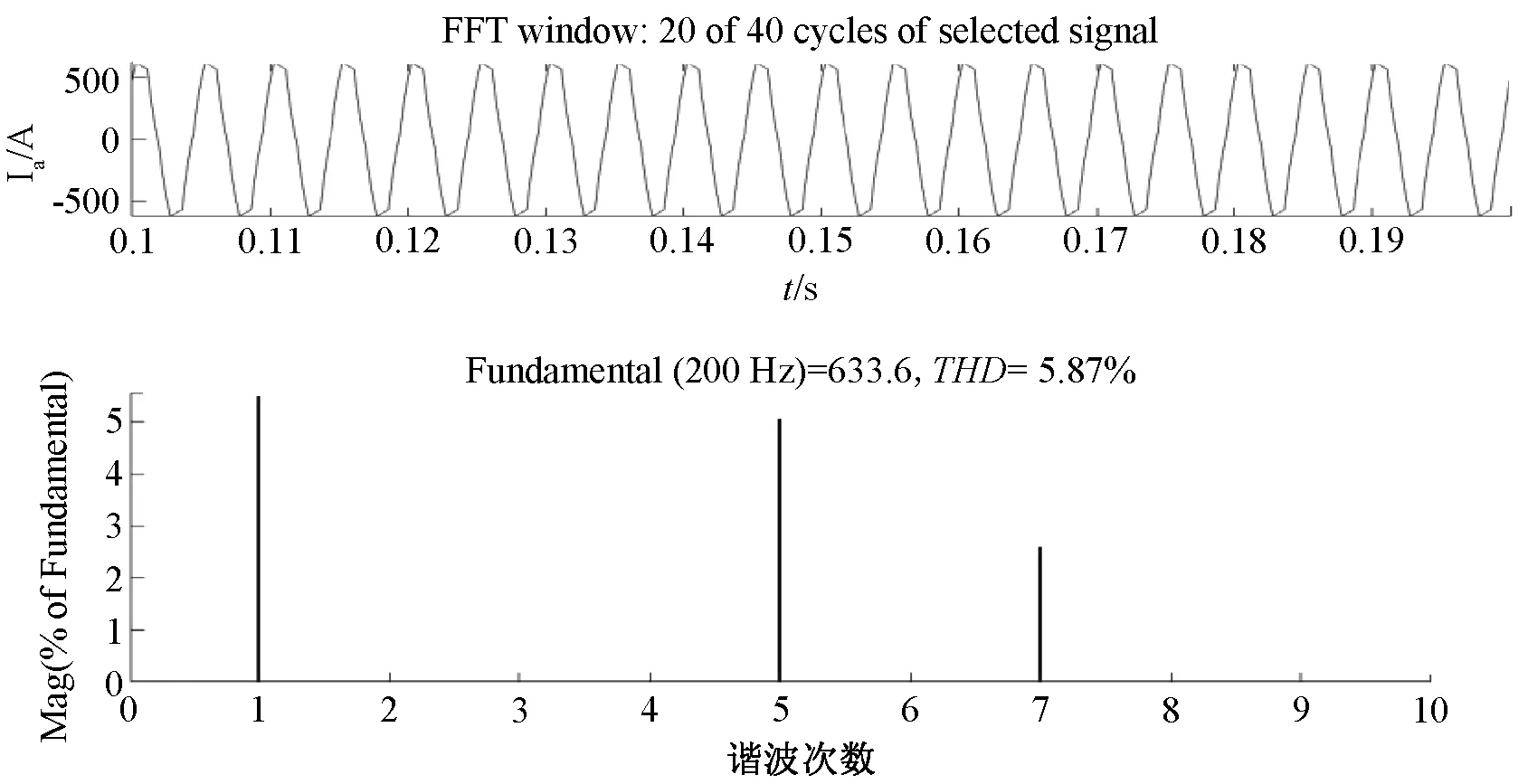
圖15 改進算法Ia及其諧波含量波形圖(3 000 r/min)
通過諧波含量對比分析可以看出,SVPWM同步過調制算法有效降低了5次和7次諧波,整體諧波含量相比傳統算法降低了2%以上。
3 改進SVPWM同步調制算法實驗
實驗設備采用100%低地板永磁牽引系統實驗平臺。直流供電電壓800 V,PMSM極數8極,額定功率106 kW,DL850示波器。

圖16 永磁牽引系統實驗柜體
以太網與牽引控制單元進行通信,觀測本文方法三脈沖和方波運行時的穩定性以及過渡切換時電流畸變情況,可驗證本方法的可行性。實驗波形如圖17、圖18所示。

圖17 SVPWM同步過調制多脈沖過渡到三脈沖
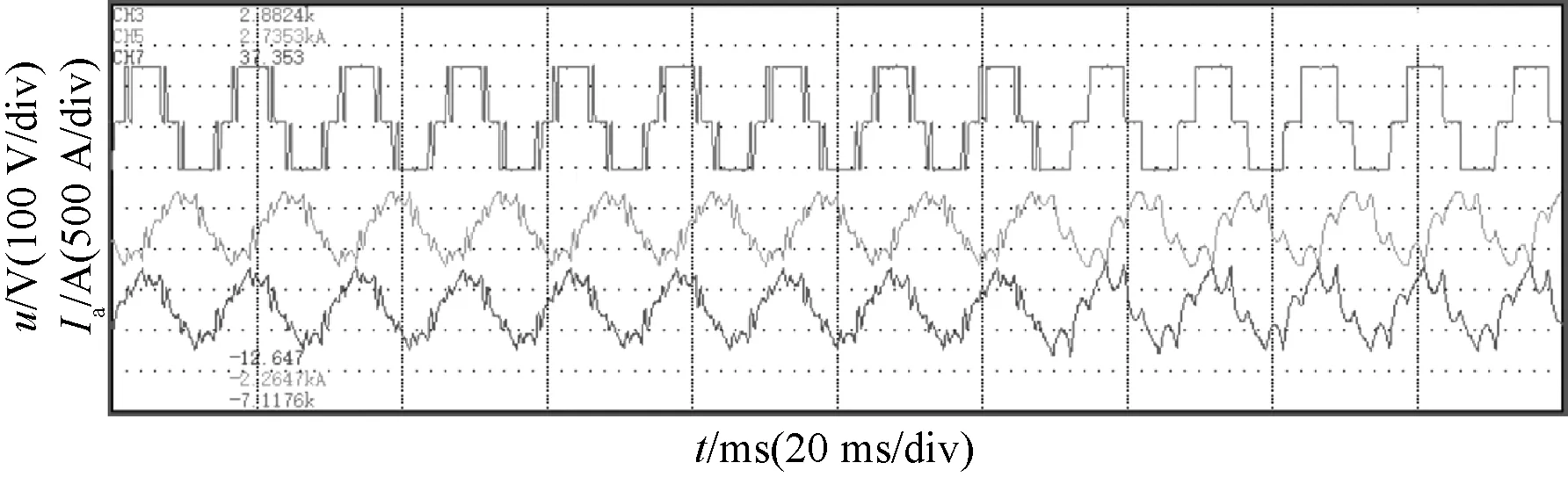
圖18 SVPWM同步過調制三脈沖過渡到方波
SVPWM同步過調制調制波連續,因此不存在多模式切換下的相位畸變,未產生電流沖擊,甚至過流保護情況。實驗驗證了本方法可實現平滑過渡到方波運行。
4 結 語
本文提出了一種PMSM SVPWM同步過調制算法,建立了數學模型和仿真模型,并且對算法進行了簡化處理,取消了過調制區計算和扇區判斷,通過檢測三相電流直接計算出空間電壓矢量作用時間,實現了異步調制和過調制運算的連續性,提高了算法運算效率。
相比傳統SVPWM同步調制算法,本方法有效降低了輸出諧波含量,降低了開關頻率,減小了逆變器發熱,提高了系統效率,減少了能耗損失。
通過仿真實驗,對比分析了輸出波形和諧波含量;進行了地面聯調實驗,實驗結果得出輸出電壓可以平滑過渡到方波運行,過渡過程沒有明顯沖擊和振蕩,從而驗證了本方法的合理性和可行性。

