基于ARIMA與線性回歸組合模型的汽車銷量預測分析*

桂思思 孫 偉 徐曉鋒

（1.武漢智慧生態科技投資有限公司 武漢 430119）（2.神龍汽車有限公司 武漢 430056）（3.武漢昱升光器件有限公司 武漢 430073）

1 引言

隨著汽車的逐漸普及，汽車在人們的出行消費中占有越來越重要的地位，而汽車行業的飛速發展與激烈競爭，也給各個品牌的主機廠提出了更高的要求，實時掌握品牌未來的汽車銷量，能夠更好按需安排生產計劃，控制汽車庫存量，更能有效地為市場部門提供有針對性的營銷數據支撐。

我們可以在各類文獻中找到關于汽車銷量的預測模型研究，如文獻［1］基于汽車市場的月度銷量進行中長期預測，提出了基于結構關系識別的汽車銷量預測方法。文獻［2］分析了我國汽車銷量的主要影響因素，如經濟環境、汽車價格、基礎設施環境等因素，并計算出各影響因素的灰色關聯分析，提出了基于回歸分析的汽車銷量預測模型。文獻［3］根據我國汽車市場的月度銷量數據，并基于具有季節調整的ARIMA進行汽車銷量預測。

筆者進行調研發現，各類預測模型并未在各品牌的汽車主機廠得到廣泛應用，分析原因主要為：1）主機廠更關注于面向單品牌的汽車銷量預測，而現有預測模型大都根據汽車市場的總體情況，分析汽車行業的宏觀影響因素進行建模，與面向單品牌的銷量預測影響因素存在差異；2）部分模型選取的預測數據對主機廠來說比較難以獲取，如有些模型需要統計全國公路里程，有些涉及品牌情感因素的分析需要抓取外部網站的數據。本文根據主機廠的數據現狀，分析面向品牌汽車銷量預測的主要因素，提出一種基于ARIMA與線性回歸組合模型的單品牌汽車銷量預測模型的建立方法。

2 影響因素分析

在汽車行業，面向普通大眾的單品牌汽車銷售流程大體為

1）單品牌的銷售線索搜集。主機廠從各大垂直網站、自媒體、以及進4S店的用戶登記數據獲取銷售線索，銷售線索記錄的往往是有購車意向的客戶信息。

2）對銷售線索進行跟進。這個過程主要是銷售人員和客戶進行溝通，跟進、價格談判等。

3）銷售線索的成交。銷售線索成交后將轉化為銷售訂單，也就是普遍意義上的汽車銷售。

從上述流程流程中可以看出，銷售線索是影響汽車銷售的一個重要因素，也是汽車品牌主機廠真正掌握的售前數據之一。另外，普通的單品牌汽車銷售會受到近期或去年同期銷售情況的影響，因此歷史銷量也是進行銷量預測的另一重要指標。下文中我們根據某汽車品牌提供的2014年～2018年銷售線索及歷史銷量數據，對影響因素進行具體分析與建模。

3 預測模型建立

3.1 模型建立方法

模型的建立方法如下四步。

步驟1提取相關因素。檢驗相關因素的相關性，提取相關性較高的相關因素作為多元線性回歸的自變量。

步驟2提取自回歸自變量。建立自回歸序列，對序列進行差分，并根據自相關和偏相關參數進一步對ARIMA模型定階。

步驟3結合步驟1和步驟2提取的自變量建立多元線性回歸模型。

步驟4對模型進行擬合、驗證及調整，對各參數顯著性進行檢驗，得到較完備的最終模型。

3.2 線性回歸模型建立

回歸分析是研究一個變量關于另一些變量的具體依賴關系的計算方法和理論，根據自變量的變化來預測因變量的變化，變化關系一般為相關關系，是統計學中一個常用的方法，被廣泛地應用于社會經濟現象變量之間的影響因素和關聯的研究。

通過R語言將該品牌的銷售線索數據與銷量數據進行相關因素分析，計算Pearson相關系數為0.8052126，可以看出該品牌的銷售線索與汽車銷量之間的相關性很高。建立以銷售線索Xi為自變量，銷量Yi為因變量的線性回歸模型如下

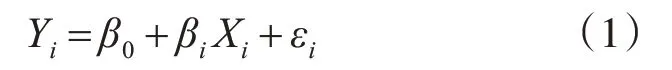
上式中β0為截距項，βi為模型的參數，誤差項εi是隨機變量。

3.3 ARIMA模型建立

該品牌汽車銷量的月度數據具有長期趨勢、季節變動，隨機波動的特點，我們選擇通過自回歸模型進行分析，自回歸模型被廣泛地應用于包含銷量預測在內的時間序列的分析與預測中。

ARIMA模型是對非平穩時間序列進行分析的方法，在對序列進行差分后建立自回歸移動平均模型，季節性的ARIMA模型是在ARIMA模型的基礎上加入了季節的考慮而改進的模型，假設對于Yt的隨機時間序列，經過d階差分后為平穩序列，模型滿足如下模型結構：

其中B為延遲算子，有BpYt=Yt-p，誤差項是當期的隨機干擾εt，為零均值白噪聲序列。其中：

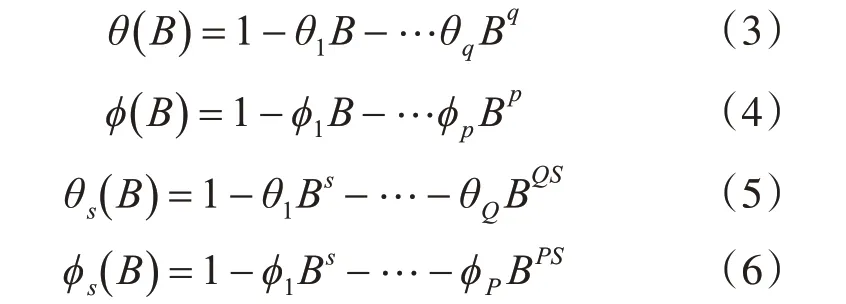
稱該模型為AR IM A(p，d，q)(P，D，Q) m

首先建立該品牌以月為單位的銷量數據的原始序列Yt，t=1，2，3，…對銷量數據進行平穩性檢查，時序圖如圖1，可以看出時序圖有明顯的遞減趨勢，單位根檢驗統計量對應的p值為0.2904，顯著大于0.05，該序列是非平穩序列，自相關圖圖2顯示，自相關系數長期大于零，說明序列間有相關性。

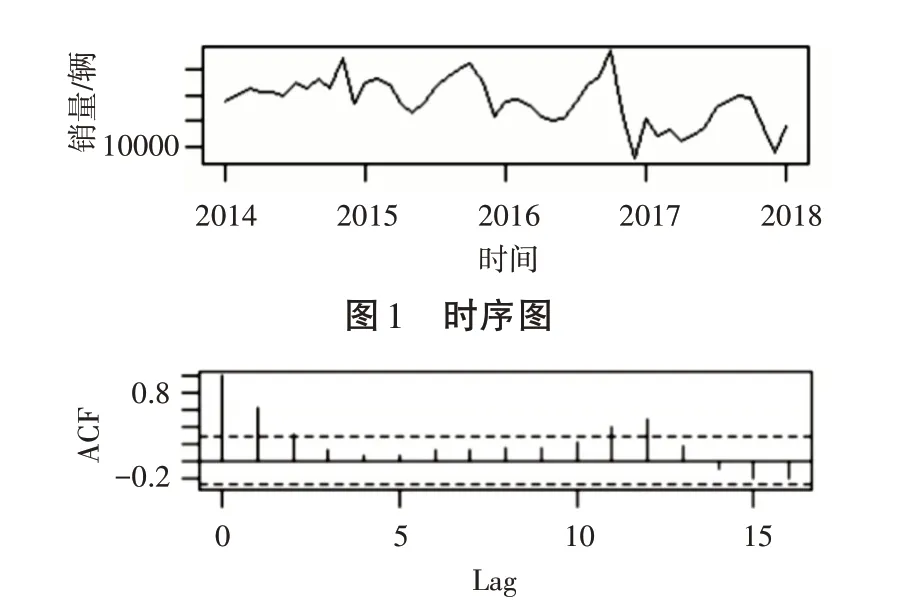
圖2 自相關圖

對序列進行一階差分?yt=?yt-?yt-1，如圖3顯示一階差分之后序列的時序圖在均值附近比較平穩的波動，進行單位根檢驗，p值為0.01，表明一階差分之后序列是平穩的。

圖3 一階差分時序圖

對一階差分后的序列進行自相關和偏相關判斷如圖4和圖5，從自相關圖和偏自相關圖可以看出，acf拖尾，pacf截尾，并且可以看出lag值延遲12階處，自相關和偏自相關系數都顯著非零，說明一階差分后序列具有季節效應。

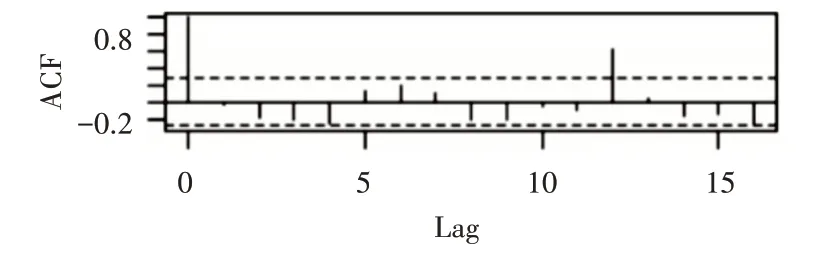
圖4 一階差分自相關圖

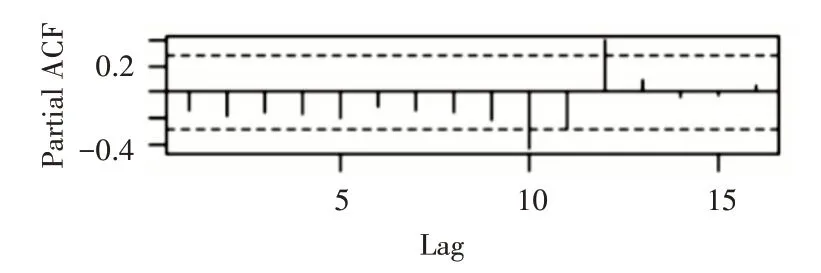
圖5 一階差分偏自相關圖

圖6 兩次差分后自相關圖

圖7 兩次差分后偏相關圖

將ARIMA（1，1，0）（0，1，0）12模型各值帶入到式（2）中，可得該品牌基于歷史銷量的時間序列表達式為

3.4 模型組合

自回歸模型本身就是多元線性回歸模型的一種，通過式（3）可以確認t時刻的隨機變量Yt是Yt-1、Yt-2、Yt-12、Yt-13、Yt-14的多元線性回歸。因此將上述自變量結合式（1），形成多元線性回歸方程（8），如下：

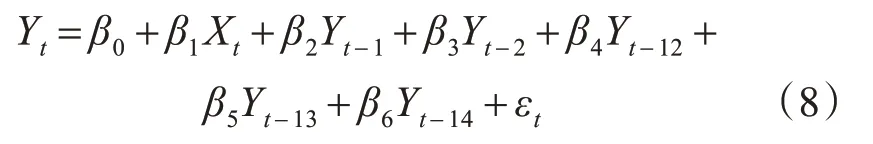
β0為截距項，β1～β6為模型的參數，Xt為t時刻銷售線索，Yt-1、Yt-2、Yt-12、Yt-13、Yt-14為對應t-1、t-2、t-12、t-13、t-14時刻的歷史銷售數據，誤差項εt為t時刻隨機變量。

4 模型驗證與調整

通過R語言進行模型驗證及參數調整，首先驗證只有銷售線索變量的模型，根據式（1）進行擬合優度檢驗，提取可決系數R2為0.5003，Rˉ2為0.4897，可以看出樣本擬合度不高，根據式（8）對組合后的模型進行擬合度檢驗，提取可決系數R2為0.8288，Rˉ2為0.8043，可決系數明顯提高，對模型進行單個變量的顯著性檢驗，各項t檢驗的p值如表1，可以看出截距項的t檢驗結果為不顯著。

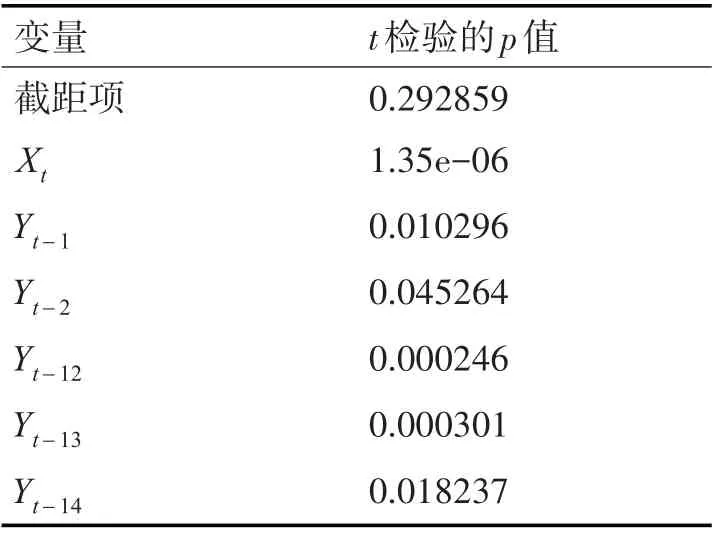
表1 式（4）各變量的t檢驗p值

剔除截距項，得到式（9）：

根據式（9）對進行擬合度檢驗，提取可決系數R2為0.9833，Rˉ2為0.981，可決系數進一步提高，對模型進行單個變量的顯著性檢驗，各項t檢驗的p值如表2，均小于0.05，模型整體顯著性檢驗F檢驗統計量為421.8，兩個自由度為6和43，對應的檢驗P值為2.2e-16，說明模型整體是顯著的。

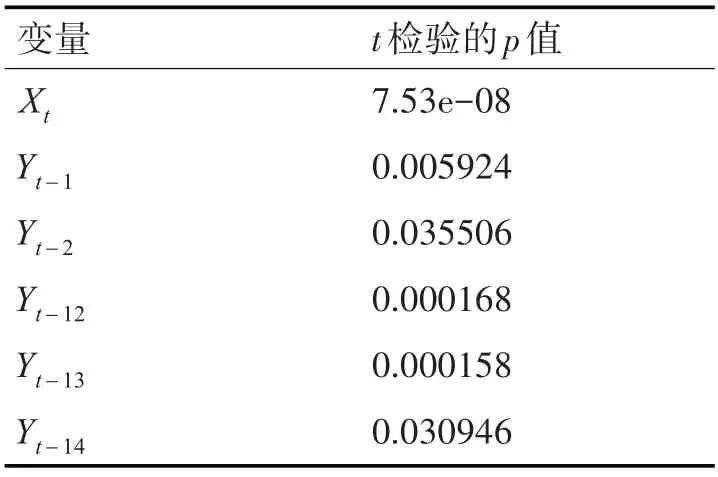
表2 式（5）各變量的t檢驗p值

根據該模型預測值的百分比誤差RPE如表3。其中RPE計算公式如式（10），其中y^t為t時刻預測值，yt真實值。

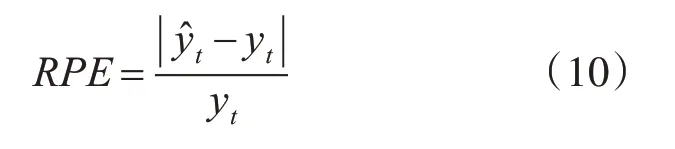
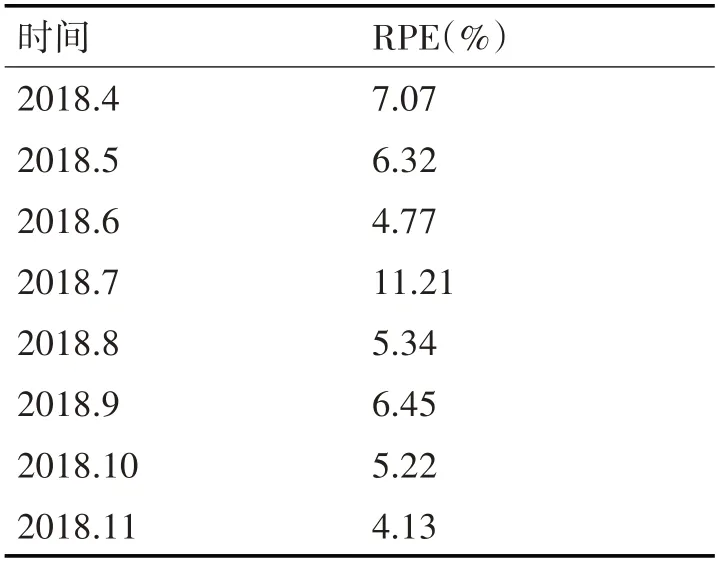
表3 預測值的百分比誤差

5 結語

該模型在對2018年4月～2018年11月的銷量預測中，除了7月RPE值較大，其他預測偏差均在8%以內，預測效果較為理想，證明了該模型建立方法的可行性。

銷售線索及歷史銷量數據是影響單品牌銷量預測的重要因素，在模型的建立過程中不可相同對待，銷售線索與銷量密切相關，可直接作為線性回歸模型的因變量處理，而歷史銷量具有趨勢性和季節性的特點對銷量預測的影響更加復雜，因此需要通過非平穩時間序列的分析進行模型因變量的提取，最后再將各個因變量進行模型組合。整個模型建立過程中線性回歸模型是建模的基礎模型，各個因變量的提取是模型建立的關鍵。本文提出建模思路及方法符合大多數汽車品牌的數據基礎，較易實現，可為面向單品牌的汽車銷量預測提供參考。