重力壩的壩與地基體系可靠度分析方法研究
熊 敏, 柯 虎, 吳 震 宇, 周 靖 人
(1.國能大渡河流域水電開發有限公司,四川 成都 610041;2.四川大學水力學與山區河流開發保護國家重點實驗室,四川 成都 610065;3.四川大學水利水電學院,四川 成都 610065)
0 引 言
隨著國家水利資源開發利用的程度不斷提高,一大批高混凝土重力壩工程投入建設和運行,如烏東德、白鶴灘、大古重力壩等。這些高壩大庫工程所處地形和氣候條件復雜,在運行過程中重力壩結構可能存在多種失效模式,因此,如何合理研究和分析大壩結構體系可靠度對于合理評價其運行安全具有重要意義。
1 已取得的研究成果
重力壩結構體系可靠度分析主要包括失效模式的識別和體系失效概率確定[1],并且已經取得較為豐富的研究成果。谷俊芹等[2]在重力壩有限元模型中利用生死單元技術和改進的階段分枝法識別失效路徑,基于逐步等效線性化Johnson求交法和條件可靠指標實現路徑的失效概率計算。王超[3]分別采用了基于塑性損傷的壩體破損模型、基于斷裂力學的壩體開裂破壞模型和基于擴展有限元的壩體開裂擴展模型,提出了復合隨機下重力壩強震失效模式的搜尋方法。康旭升等[4]結合實例分析了傳統的微分等價遞歸算法、改進的微分等價遞歸算法和條件概率降維算法的優缺點、使用范圍和存在的問題。張社榮等[5]用描述變量相關的Copula理論建立了重力壩層間抗滑穩定的體系可靠度計算模型,克服了基于獨立性假設的一階、二階區間估計等方法的局限性。徐強等[6]用貝葉斯公式和柯西-施瓦茨不等式計算各失效模式的失效概率和體系失效概率,具有考慮失效路徑多、安全性評價方法多的優點。李會軍等[7]將iHLRF算法、梯度投影法(GPA)、Polak-He算法和SQP(序列二次規劃法)引入重力壩的構建可靠度計算。胡魏玲等[8]提出可以用僅考慮主次失效模式相關性的主次失效模式相關系數簡化模型計算重力壩結構系統可靠度,并通過算例證明該模型的適用性。趙澤鵬等[9]應用了Ditlevsen窄界限法、T-DERA法、M-DERA法、DRMCP法、PNET法計算,探討了各種方法在復雜地基重力壩體系可靠度計算中的差異性與實用性。
重力壩的失效模式一般包括壩趾壓壞、壩踵拉裂、沿建基面或深層滑動及傾覆等。相關學者[10-12]在考慮分析重力壩體系可靠度時通常從以上失效模式中選取壩址壓碎、壩踵拉裂和壩基面抗滑穩定作為主要的失效模式,這種失效模式確定方法存在一定的主觀性。基于此,在識別重力壩壩與地基系統的失效模式基礎上,通過構建壩體破壞及地基失穩的功能函數及響應面方程,提出重力壩體系可靠度分析的Monte Carlo法,并將其應用于某重力壩工程,驗證其可行性和適用性。
2 體系可靠度分析方法
2.1 失效模式和功能函數
這里,采用彈塑性增量分析法來分析其失效模式,也稱彈塑性超載法[13]。對于重力壩而言,可以利用Drucker-Prager 準則和抗剪斷公式來構建壩體破壞及壩基抗滑穩定的功能函數。根據Drucker-Prager 準則[14-15]建立壩體單元失效的功能函數為:
(1)
式中a、k均為與材料黏聚力c和內摩擦角φ有關的常數;I1為應力張量第一不變量;J2為應力偏張量第二不變量;I1,J2表達式分別為:
I1=σ1+σ2+σ3
(2)
(3)
式中σ1,σ2,σ3分別為第一第二第三主應力。
破壞軌跡選取常用的外角外接圓,則a、k的取值如下:
(4)
式中,φ為內摩擦角,c為黏聚力。
根據抗剪斷公式建立滑移失效模式的功能函數為:
(5)
重力壩結構體系應是多種失效模式組成的串聯體系,當任意一種失效模式發生時,即某個失效模式的功能函數Z<0時,認為該重力壩失效。串聯系統的失效概率Pfs的表達式為
(6)
式中P{·}為隨機事件發生的概率;gj(X)為第j中失效的功能函數;E[gj(X)<0]代表重力壩因第i種失效模式失穩的事件;m為失效模式的種數;X=X1,X2,…Xn為影響重力壩體系可靠度的主要隨機變量;n為隨機變量的個數。
2.2 體系可靠度計算
實際工程中結構功能函數Z與隨機變量X之間的函數關系難以顯式表達,在工程和實際計算中通常采用響應面法[16]。目前工程中所使用的響應面方程形式多為不含交叉項的二次多項式:

(7)
式中a0,bi,ci為待定系數(i=1,2,…,m);xi為隨機變量。
當用響應面法擬合出功能函數Z與隨機變量X之間的關系后,采用蒙特卡洛法(Monte Carlo Method)計算體系可靠度。對于體系可靠度,用蒙特卡洛法可表示為:

=1,2……,m
(8)

I[g1(X),g2(X),…,gj(X)]=
(9)
3 案例分析
3.1 有限元模型及參數
某碾壓混凝土重力壩壩頂高程1 135.0 m,該重力壩的9號壩段為河床非溢流壩段,壩段高度148 m,該大壩9號壩段剖面見圖1。根據開挖地質揭示情況可知,壩基巖體以Ⅲ1、Ⅲ2類巖為主。該電站壩址區緩傾角錯動帶和緩傾角裂隙較為發育,其中9號壩段下的裂隙和錯動帶發育。可能構成危險滑移通道的裂隙為:④N25°~30°W/SW∠30°~40°。可能構成危險滑移通道的錯動帶有:fx9-1:產狀N80°E/SE∠40°;fx10-5:產狀N70°E/SE∠10°~20°;fx10-4:產狀EW/S∠15°。上述裂隙和錯動帶組成一條滑移通道。該滑移通道共包含4個滑裂面,且沿第④組裂隙從壩趾處滑出。

圖1 某重力9號壩壩段剖面
地基的建模范圍為:從建基面向下延伸取兩倍壩高,從壩踵和壩址分別向上游和下游延伸2倍壩高,橫河向寬度取9號壩段的實際壩段寬度20 m。模型單元均采用solid45單元類型,結點總數12 201,單元總數13 445,有限元模型見圖2。9號壩段壩體和材料基本參數見表1。計算時主要考慮的荷載有:壩體上下游表面靜水壓力(正常蓄水位高程1 131 m,相應下游水位高程1 003.5 m),揚壓力(揚壓力強度系數α=0.25)。
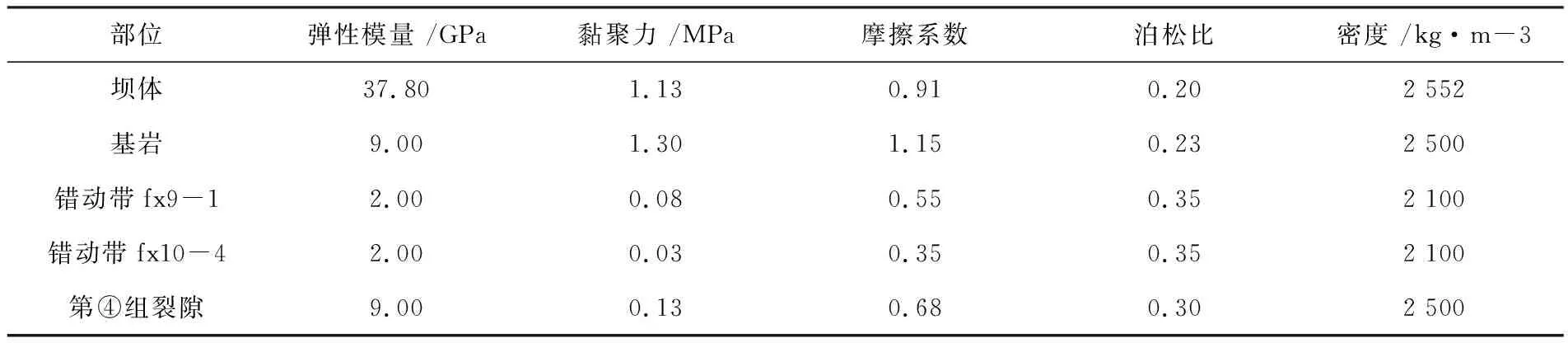
表1 9號壩段壩體及壩基材料基本參數建議值

圖2 有限元模型
3.2 主要失效模式搜尋
依據壩與地基整體超載模擬得到的塑性區的開展情況,確定了該重力壩9號壩段重力壩壩體-壩基體系的兩種主要失效模式(圖3):1.壩踵處失效路徑貫通;2.壩體沿深層滑移通道滑動。

圖3 失效模式示意圖
壩體混凝土和基巖容重、泊松比、結構尺寸等變異系數較小,這里不考慮其隨機性。本次模型計算中主要考慮壩體、地基以及構成壩體深層滑移通道的兩種錯動帶和一種裂隙的彈性模量E、凝聚力c′、摩擦系數f′及上游水位共15個隨機變量,其隨機變量統計特征見表 2。

表2 隨機變量統計特征
3.3 響應面方程構建
由公式(1)、(2)和(4),可以構建該重力壩壩體失效和壩體穩定失效的響應面方程。其中,壩體單元失效響應面方程為:
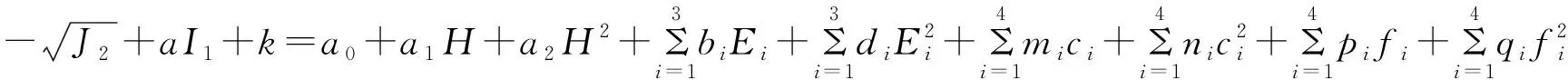
(10)
式中a,k,I1,J1的含義與公式(1)中相同;H為水深;Ei為材料的彈性模量;ci為材料的黏聚力;fi為第i中材料的摩擦系數;ai,bi,di,mi,ni,pi,qi為響應面方程的待定系數。
滑移失效響應面方程:

(11)

3.4 體系可靠度分析
這里采用重力壩體系可靠度計算方法,可得到單一失效通道可靠度和體系可靠度(見表3)。壩體失效模式β=4.73,深層滑移失效模式β=5.02,均滿足規范中規定的Ⅰ級水工建筑物構件目標可靠度βt>4.2要求。此外,壩體失效模式的可靠度小于深層滑移失效模式的可靠度,說明壩體失效模式是該壩段主要的失效模式。壩與地基的體系可靠度指標β=4.69,小于壩體失效模式和深層滑移失效模式的可靠度指標,體系可靠度相對于壩體失效可靠度的降低值為0.33,相對于深層滑移失效可靠度的降低值為0.04。研究表明,體系可靠度相對于單一失效模式可靠度的降低幅度都會有所不同。在失效概率方面,該壩段體系失效概率為1.34×10-6,壩體失效概率為1.12×10-6,深層滑移失效概率為2.62×10-7。考慮多種失效模式下的體系失效會使失效概率增加,反映了重力壩整體的安全狀況,只考慮單一失效模式會使安全性評價偏于危險。

表3 可靠度指標和失效概率
4 結 語
可靠度是反映重力壩結構安全穩定的重要指標之一,研究復雜地質條件下混凝土重力壩體系可靠度具有重要的工程意義。
(1)通過采用彈塑性增量分析法來搜索重力壩壩與地基整體失效模式,以DP準則和抗剪斷準則構建壩體及地基失效的功能函數,確定了多種失效模式下壩與地基串聯體系可靠度的MonteCarlo方法。
(2)某重力壩結構體系研究顯示,其整體失效模式為壩踵破壞和壩基穩定破壞,壩與地基的體系可靠度為4.69,較單一失效模式下壩踵破壞或者壩基穩定破壞小。
(3)研究表明傳統單一失效模式下結構可靠度分析偏于危險,采用體系可靠度來綜合評價工程結構的實際安全狀況更符合工程實際。此方法具有一定的工程推廣意義。

