結構化教學:讓數學學習充滿生長的力量
錢蔚

“圓柱的體積”是蘇教版數學教材六年級下冊的教學內容,是在學生學習了圖形的認識、圖形的面積以及長方體、正方體的表面積、體積后需要學習的幾何知識。教材是這樣安排的:復習長方體、正方體的體積公式,引導學生猜想圓柱與長方體、正方體體積之間的關系,引發學生思考、驗證,推導出圓柱體的體積公式。教材做出這樣的安排,是基于學生認知水平和已有經驗,不斷豐富對圖形轉化的體驗,從而加深對公式的理解。我們在結構化教學思想的指導下,基于學生,立足教材,開展結構化教學設計。以整體視野尋找知識間內在的、縱橫交錯的本質聯系,使學生在學習過程中不僅學會知識、理解知識,還形成知識結構、方法結構,從而發展學生的結構化思維,提升學生的思維品質。
一、激活知識經驗,讓認知結構悄然發生
我們知道,一切學習都是建立在學生已有認知基礎之上的。認知教育心理學家奧蘇貝爾說:“如果我不得不將教育心理學還原為一條原理的話,我將會說,影響學習的最重要因素是學生已經知道了什么。”結構化學習應“基于知識整體單元的發生與發展,凸顯知識元素間的溝通與聯系”,“是將教材的學科結構轉變為學生的認識結構的學習,是學生的認知發展規律與知識發生規律相融合的學習”。為此,在結構化教學中,教師的任務之一是激活學生的經驗,幫助學生熟悉知識的展開結構,從而讓學生的認知結構悄然形成。
【教學片段一】
師:前幾節課研究了圓柱的認識和表面積,猜想這節課要研究什么內容了?你為什么這么猜?
生:要學習圓柱的體積了,根據上學期學習長方體、正方體的內容順序猜的。
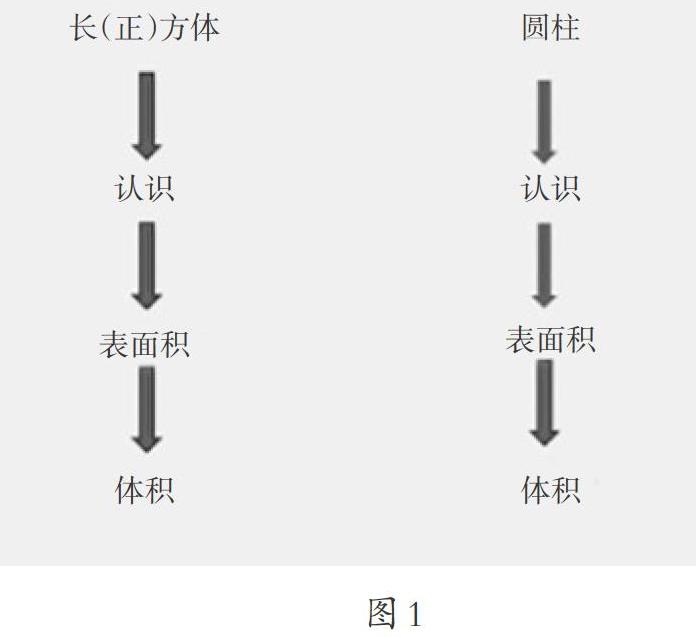
根據學生的回答教師出示圖1。
師(小結):在學習長方體和正方體這一單元時,我們經歷了這樣一個學習序列,由此經驗可以猜想到圓柱的學習序列也許就是這樣的。經驗很重要,它能讓我們產生猜想。
(板書:經驗,猜想)
師:根據以往學習經驗,再猜想下,我們要研究哪些問題?
生:圓柱體積怎么求呢?有沒有像長方體、正方體那樣的公式?
生:圓柱體積與什么有關?
生:圓柱體積與長方體體積有什么聯系?
【思考】在這個教學片段中,教師沒有開門見山出示“圓柱的體積”課題,而是讓學生依據學習經驗猜想學習內容。如此設計,能讓學生打開思維的閘門,主動搜索,積極聯系,使學生從整體上感悟“立體幾何圖形”學習的知識結構。隨著學習的進一步深入,這些知識結構將逐步轉變為學生個體的認知結構。“我們要研究哪些問題?”這個問題,不僅起到培養學生問題意識的作用,更能啟發學生產生積極的聯想,讓知識結構在學生的頭腦中悄悄地形成。
二、探尋結構關聯,為深度思維導航
數學是思維的科學,努力促進學生思維的發展是數學教學的重要目標。事實上,在解決問題的過程中,并非只有獨立的某個知識在發揮作用,而是整個知識結構在起作用。因此,教師要幫助學生建立合理的認知結構,發展結構化思維。特級教師許衛兵說過,當學習總是在結構關聯中展開,當問題解決、探索發現總是不斷被結構性的力量“征服”時,結構化思維的種子就會在播種、萌芽、破土、生長后開花結果。
【教學片段二】
師:圓柱體積怎么求呢?看看圓柱的樣子,根據以往學習的經驗,你有什么想法?
生:是否可以把圓柱轉化成長方體?
師:為什么會有這樣的猜想?
生:在學習圓的時候,將圓這個曲線圖形轉化成長方形研究了它的面積,研究圓柱這個曲面圖形我就突然有了這個猜想。
(如圖2,教師利用多媒體幫助學生回憶圓面積的推導過程)
師:學習經驗真的很重要,它又一次讓我們有了猜想。這個猜想是否正確?怎么辦?
生:我們可以試一試。
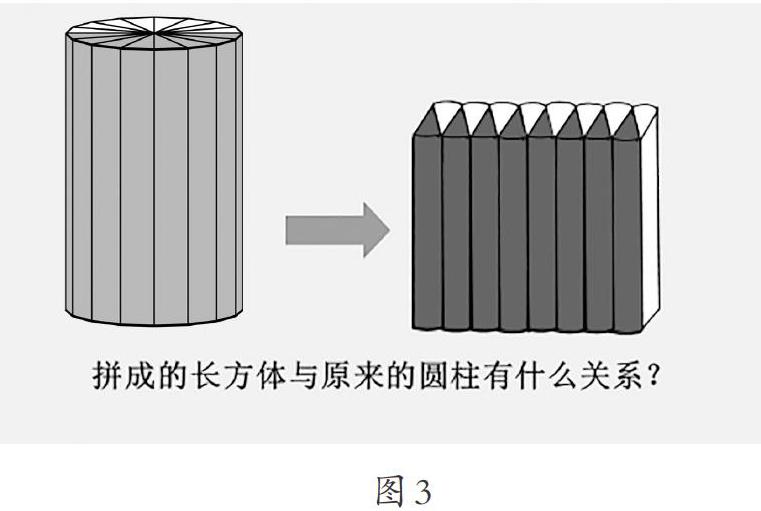
(學生以小組為單位動手用學具操作驗證,然后多媒體展示,并讓學生感受到:沿著底面半徑和高切分,平均分的份數越多,越接近長方體,如圖3)
師:根據以往的經驗,轉化成功后我們該干什么?
生:要尋找轉化前后的聯系。
師:我們今天研究的是圓柱的體積,圓柱被我們轉化成了長方體。那么,我們在尋找聯系的時候,要從哪些方面去找呢?
(教師根據學生的觀察與發現形成圖4)
【思考】在這個教學片段中,圓柱的體積在經過“鼓勵猜想、動手實踐、尋找聯系”這三個環環相扣的學習環節后,體積公式呼之欲出。“鼓勵猜想”是教師為學生搭建經驗與新知產生關聯的橋梁。因為在圓的知識學習過程中,學生經歷了“化曲為直、化圓為方”的學習過程,這一經歷能有效地誘發學生將圓柱轉化為長方體的猜想。“動手實踐”是猜想驗證的必要環節,也是“尋找聯系”環節的基礎。有的教師為了省時省力,在這一環節采用教師演示或多媒體演示的方式進行。教學結果表明,這些都不能使學生真正體驗感知圓柱與長方體之間的關聯,只有讓學生做一做、看一看、想一想之后,才能建構起數學知識的完整樣態,促進數學思維的深度發展,從而培養學生的數學核心素養。
三、反思探究過程,幫助學生生成結構
學生依循教師“教結構”的步驟獲得了新的知識結構,也在親歷數學探究的過程中感受了方法結構,但這對于小學生而言還是模糊的。教學中,教師要有意識地設計回顧反思探究知識的環節,幫助學生生成結構。
【教學片段三】
師:千金難買回頭看,“圓柱的體積”這個新課題我們是怎么研究成功的?
(教師根據學生回答完善板書:依據經驗—提出猜想—動手驗證—尋找關聯)
師:是的,學習是不斷積累經驗的過程,經驗越多,越能發現知識之間的聯系、學習方法之間的聯系。因此,有這樣一句話送給同學們:數學知識之間的聯系是構建思維體系的骨架。希望大家在面對一個新知識的時候,先想一想,它會與我們學過的哪些知識有聯系?可以用我們學過的哪些方法來研究?這樣的學習,會使你變得越來越聰明。
【思考】在得出圓柱的體積公式之后,教師并沒有馬上進入練習環節,而是追問學生:我們是怎么研究的?讓學生通過回顧、梳理、交流,明確學習的過程結構。認識到這種過程結構的存在,學生就可以在以后的學習中主動遷移和應用這一過程結構。
數學,常常被稱為“結構的科學”。教學中,我們不僅要教給學生結構化的知識,更要教給學生獲取結構化知識的方法。
(作者單位:江蘇省無錫市查橋實驗小學)

