渦扇發(fā)動(dòng)機(jī)的一類(lèi)大包線(xiàn)系統(tǒng)建模

凌彥聰，周文祥，朱平芳，曾建平

（1.廈門(mén)大學(xué)航空航天學(xué)院，廈門(mén) 361005；2.南京航空航天大學(xué)能源與動(dòng)力學(xué)院，南京 210016）

非線(xiàn)性和時(shí)變是渦扇發(fā)動(dòng)機(jī)系統(tǒng)中普遍存在的現(xiàn)象，高精度的非線(xiàn)性時(shí)變數(shù)學(xué)模型是渦扇發(fā)動(dòng)機(jī)特性分析和綜合的基礎(chǔ)。早期渦扇發(fā)動(dòng)機(jī)建模方法，大都采用線(xiàn)性化模型，未能真實(shí)地反映渦扇發(fā)動(dòng)機(jī)系統(tǒng)時(shí)變和非線(xiàn)性的動(dòng)態(tài)信息。針對(duì)這一問(wèn)題，吳斌等［1］建立線(xiàn)性變參數(shù)（Linear parameter?varying，LPV）模型描述渦扇發(fā)動(dòng)機(jī)大范圍變化的動(dòng)態(tài)特性，LPV 系統(tǒng)的系統(tǒng)參數(shù)可以表示為參數(shù)的函數(shù)，是基于狀態(tài)的增量形式，需要與穩(wěn)態(tài)基線(xiàn)模 型 結(jié) 合 使 用。Fu 等［2?3］提 出 一 類(lèi) 能 夠 描 述 對(duì) 象非線(xiàn)性和時(shí)變特性的非線(xiàn)性變參數(shù)（Nonlinear pa?rameter?varying，NPV）模型。該模型將非線(xiàn)性特性表征為依賴(lài)狀態(tài)的多項(xiàng)式函數(shù)，其狀態(tài)是基于對(duì)象的物理量，但由于其不需要基線(xiàn)模型則會(huì)帶來(lái)誤差的積累。因此，在擬合成NPV 模型之前如何高精度地對(duì)各個(gè)穩(wěn)態(tài)點(diǎn)以及各包線(xiàn)的建模就顯得至關(guān)重要。本文采用系統(tǒng)辨識(shí)的思想研究渦扇發(fā)動(dòng)機(jī)的NPV 系統(tǒng)建模方法。

關(guān)于渦扇發(fā)動(dòng)機(jī)模型辨識(shí)可以分為兩類(lèi)：一是對(duì)試驗(yàn)數(shù)據(jù)的辨識(shí)修正提高部件法模型的精度。二是選擇輸入輸出數(shù)據(jù)以及模型類(lèi)進(jìn)行辨識(shí)建模。美國(guó)路易斯研究中心較早地研究系統(tǒng)辨識(shí)理論在發(fā)動(dòng)機(jī)控制系統(tǒng)設(shè)計(jì)中的應(yīng)用，Banazadeh等［4］提出一種掃頻方法，通過(guò)發(fā)動(dòng)機(jī)頻域響應(yīng)得到其 頻 率 響 應(yīng) 函 數(shù)。Kaufman 等［5］提 出GE7 燃 氣 輪機(jī)建立狀態(tài)變量模型的分步辨識(shí)方法。Breikin等［6］通過(guò)對(duì)發(fā)動(dòng)機(jī)穩(wěn)態(tài)點(diǎn)的輸入輸出數(shù)據(jù)，利用最小二乘法辨識(shí)狀態(tài)空間系統(tǒng)矩陣參數(shù)得到發(fā)動(dòng)機(jī)多變量的狀態(tài)變量模型。Norton 等［7］研究不同的輸入燃油信號(hào)對(duì)發(fā)動(dòng)機(jī)時(shí)間序列模型辨識(shí)的影響，提出計(jì)算發(fā)動(dòng)機(jī)時(shí)間序列模型參數(shù)的方法。As?gari 等［8］與郭政波等［9］提出NARMAX 模型利用正交分解法對(duì)發(fā)動(dòng)機(jī)起動(dòng)過(guò)程進(jìn)行系統(tǒng)辨識(shí)，建立發(fā)動(dòng)機(jī)非線(xiàn)性模型。隨著航空發(fā)動(dòng)機(jī)多變量控制規(guī)律研究的深入，國(guó)內(nèi)也相應(yīng)地展開(kāi)渦扇發(fā)動(dòng)機(jī)模型辨識(shí)領(lǐng)域的研究，姜銳［10］、吳斌［11］等學(xué)者采用正弦燃油信號(hào)通過(guò)頻率響應(yīng)的方法得到渦扇發(fā)動(dòng)機(jī)狀態(tài)依賴(lài)的傳遞函數(shù)。鄭斐華［12］提出了采用偽隨機(jī)信號(hào)基于系統(tǒng)辨識(shí)的航空發(fā)動(dòng)機(jī)建模方法。

基于上述討論，本文借助部件模型、系統(tǒng)辨識(shí)等方法，使用混合信號(hào)充分刺激部件模型，將某渦扇發(fā)動(dòng)機(jī)建模成NPV 系統(tǒng)，該系統(tǒng)能完整地反映渦扇發(fā)動(dòng)機(jī)非線(xiàn)性和狀態(tài)參數(shù)在大范圍內(nèi)快速變化的時(shí)變特性［13］，更加接近實(shí)際對(duì)象，為渦扇發(fā)動(dòng)機(jī)的控制提供一種新途徑。

1 NPV 模型

考慮如下NPV 系統(tǒng)

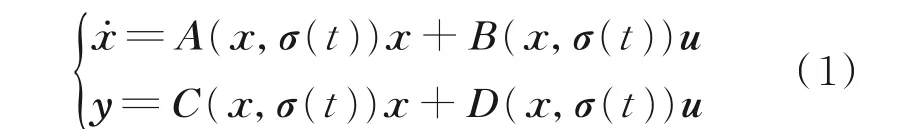
式中：x∈Rnx、u∈Rnu和y∈Rny分別為系統(tǒng)狀態(tài)、系 統(tǒng) 輸 入 和 輸 出，σ(t)∈Rnσ為 時(shí) 變 參 數(shù)，A(x，σ(t))、B(x，σ(t))、C(x，σ(t))和D(x，σ(t))為關(guān)于x和σ(t)的多項(xiàng)式函數(shù)。

工程中許多被控對(duì)象可采用NPV 系統(tǒng)作為其模型［2?3］。特別地，當(dāng)系統(tǒng)（1）的系統(tǒng)矩陣只依賴(lài)時(shí)變參數(shù)時(shí)，退化為線(xiàn)性變參數(shù)系統(tǒng)

當(dāng)系統(tǒng)矩陣僅為關(guān)于狀態(tài)量的多項(xiàng)式時(shí)，系統(tǒng)（1）退化成多項(xiàng)式非線(xiàn)性系統(tǒng)

因此，NPV 系統(tǒng)可以看作是多項(xiàng)式非線(xiàn)性系統(tǒng)和LPV 系統(tǒng)的推廣。

值得注意的是，文獻(xiàn)［1］將渦扇發(fā)動(dòng)機(jī)模型建成如式（2）所示的LPV 系統(tǒng)，其系統(tǒng)矩陣是關(guān)于高壓轉(zhuǎn)子轉(zhuǎn)速絕對(duì)量的多項(xiàng)式，而狀態(tài)則是其增量形式，形如

該建模方式只是原系統(tǒng)在工作點(diǎn)的一階近似，系統(tǒng)參數(shù)依舊只是調(diào)度參數(shù)，忽略了渦扇發(fā)動(dòng)機(jī)系統(tǒng)的強(qiáng)非線(xiàn)性。本文借助部件級(jí)模型和系統(tǒng)辨識(shí)等方法，使用混合信號(hào)充分激勵(lì)部件級(jí)模型，把渦扇發(fā)動(dòng)機(jī)系統(tǒng)建模成如下多項(xiàng)式模型

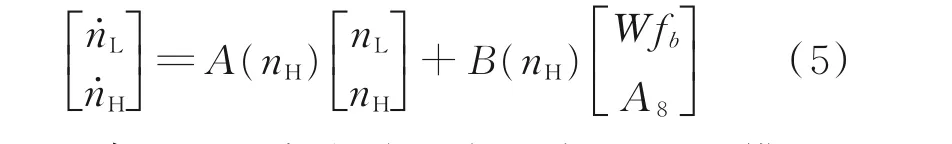
繼而建立了渦扇發(fā)動(dòng)機(jī)全包線(xiàn)的NPV 模型，系統(tǒng)矩陣是發(fā)動(dòng)機(jī)狀態(tài)和時(shí)變參數(shù)的多項(xiàng)式，顯式地體現(xiàn)渦扇發(fā)動(dòng)機(jī)的非線(xiàn)性和時(shí)變特性，彌補(bǔ)LPV 系統(tǒng)建模的不足。

2 渦扇發(fā)動(dòng)機(jī)大包線(xiàn)建模方法

以某型小涵道比雙軸渦扇發(fā)動(dòng)機(jī)為研究對(duì)象，其非線(xiàn)性數(shù)學(xué)模型可以描述為［14］

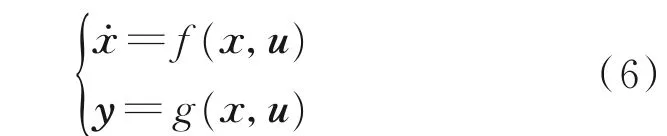
式中：x∈Rnx、u∈Rnu和y∈Rny分別為系統(tǒng)狀態(tài)、系統(tǒng)輸入和輸出。

2.1 單個(gè)穩(wěn)態(tài)點(diǎn)狀態(tài)變量模型

設(shè)(xe，ue，ye)為 渦 扇 發(fā) 動(dòng) 機(jī) 系 統(tǒng) 的 一 個(gè) 穩(wěn) 態(tài)點(diǎn)，該穩(wěn)態(tài)點(diǎn)附近系統(tǒng)（6）可化為

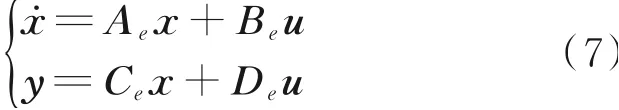
式中：Ae、Be、Ce、De為待定系統(tǒng)矩陣。

本 文 選 擇x=[nLnH]T，u=[Wfb A8]T，y=[nHπ]T，其中，nL為低壓轉(zhuǎn)子轉(zhuǎn)速，nH為高壓轉(zhuǎn)子轉(zhuǎn)速，Wfb為主燃油量，A8為喉道面積，π為發(fā)動(dòng)機(jī)的增壓比。

設(shè)采樣周期為T(mén)，kT時(shí)刻的狀態(tài)、輸入和輸出分別記為x(k)、u(k)和y(k)，采用歐拉積分的方法離散化如下

假設(shè)發(fā)動(dòng)機(jī)非線(xiàn)性模型在穩(wěn)態(tài)點(diǎn)(xe，ye)附近受擾動(dòng)信號(hào) Δu生成了輸入輸出數(shù)據(jù)：{(x(k)，y(k))，k=0，1，…，N}，N為采樣個(gè)數(shù)。

記偏差量數(shù)據(jù)矩陣為

基于最小二乘法，在部件級(jí)模型的狀態(tài)量與狀態(tài)空間模型的狀態(tài)量誤差平方和最小情況下，則系統(tǒng)矩陣參數(shù)的解為

由式（9）可確定在穩(wěn)態(tài)點(diǎn)(xe，ue，ye)模型（7）。

2.2 典型工作點(diǎn)的多項(xiàng)式模型

在某一飛行條件下，即取固定高度H和馬赫數(shù)Ma，選 取N1個(gè) 穩(wěn) 態(tài) 點(diǎn) (xei，uei，yei)，i=1，2，…，N1。對(duì)穩(wěn)態(tài)點(diǎn)(xei，uei，yei)，按2.1 節(jié)中方法得到模型參數(shù)矩陣為(Aei，Bei，Cei，Dei)。采用多項(xiàng)式擬合方法，建立典型工作點(diǎn)的發(fā)動(dòng)機(jī)多項(xiàng)式非線(xiàn)性模型

非線(xiàn)性系統(tǒng)（13）中系統(tǒng)矩陣求解步驟如下：

（1）記

則由實(shí)例點(diǎn)構(gòu)成的集合為

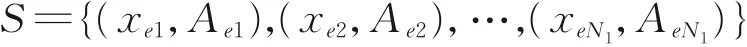
記F是由xei到Aei的函數(shù)集合，則

令h(x)=ωx，ω=[ω1…ωN1]T為 多 項(xiàng)式模型的系數(shù)向量。

由于渦扇發(fā)動(dòng)機(jī)nH更能近似反映發(fā)動(dòng)機(jī)的機(jī)械載荷和熱載荷變化狀況［16］，以及直接反映動(dòng)態(tài)特性變化，故式（13）中系統(tǒng)矩陣只為nH的函數(shù)。

2.3 大包線(xiàn)NPV 模型

在飛行包線(xiàn)內(nèi)，選取N2個(gè)典型工作點(diǎn)(Mai，Hi)，i=1，2，…，N2。按2.2 節(jié)中方法建立第i(i=1，2，…，N2)個(gè)典型工作點(diǎn)的多項(xiàng)式模型

在 包 線(xiàn) 0 ≤Ma≤1.2，0 ≤H≤8 內(nèi)，將(A(x)(Mai，Hi)，B(x)(Mai，Hi)，C(x)(Mai，Hi)，D(x)(Mai，Hi))，i=1，2，…，N2，利 用 回 歸 算 法 分 別 擬 合 成 如 下形式

σ(t)=(Ma，H)是關(guān)于高度和馬赫數(shù)的多項(xiàng)式函數(shù)，則得到渦扇發(fā)動(dòng)機(jī)大包線(xiàn)模型。

3 某型渦扇發(fā)動(dòng)機(jī)建模

本部分基于系統(tǒng)辨識(shí)的方法在不同飛行條件下獲取不同高壓轉(zhuǎn)速下的狀態(tài)空間模型，再通過(guò)多項(xiàng)式擬合和回歸方法獲取各系統(tǒng)矩陣關(guān)于時(shí)變參數(shù)與狀態(tài)變量的多項(xiàng)式描述。為了消除數(shù)據(jù)特征之間的量綱影響，將調(diào)度參數(shù)歸一化至[0，1]。

3.1 激勵(lì)信號(hào)及辨識(shí)算法

根據(jù)流量連續(xù)和功率平衡的共同工作方程建立的部件級(jí)模型，對(duì)其信號(hào)激勵(lì)得到輸入輸出數(shù)據(jù)。采用階躍信號(hào)沖擊部件級(jí)模型得到的輸入輸出數(shù)據(jù)無(wú)法刻畫(huà)渦扇發(fā)動(dòng)機(jī)的動(dòng)態(tài)特性，且一步求解最小二乘問(wèn)題時(shí)擬合程度不高。若要達(dá)到較好的辨識(shí)效果，則需多步系統(tǒng)辨識(shí)，計(jì)算量較大且動(dòng)態(tài)過(guò)程一般。因此，有學(xué)者采用偽隨機(jī)序列［17］（Pseudo random binary sequence，PRBS）沖擊部件級(jí)模型，PRBS 是由周期性數(shù)字序列經(jīng)過(guò)濾波處理得到，具有可重復(fù)性、自相關(guān)性能好的特點(diǎn)，如圖1所示。經(jīng)過(guò)仿真驗(yàn)證，相比使用階躍信號(hào)，采用PRBS 能夠充分激勵(lì)部件級(jí)模型，得到更好的結(jié)果，但其結(jié)果模型泛化性能很差。

圖1 偽隨機(jī)序列Fig.1 Pseudo random binary sequence

本文結(jié)合機(jī)器學(xué)習(xí)中訓(xùn)練集的思想，提出一種基于階躍信號(hào)、正弦信號(hào)以及偽隨機(jī)信號(hào)的混合信號(hào)。采用上下界幅度在穩(wěn)態(tài)燃油幅度的±2%左右的混合信號(hào)，即一定幅度的M 序列，階躍信號(hào)以及一定幅值和頻率的正弦信號(hào)，如圖2所示。相比使用單一信號(hào)，采用混合信號(hào)可以充分激勵(lì)部件模型，得到更好的結(jié)果，且結(jié)果模型泛化性能較好。

圖2 混合信號(hào)Fig.2 Mixed signal

辨識(shí)采用的最小二乘算法為L(zhǎng)evenberg?Mar?quardt（L?M）估計(jì)算法［18］。L?M 算法的每一步迭代都可以調(diào)整阻尼項(xiàng)以確保誤差下降。當(dāng)遠(yuǎn)離最優(yōu)解時(shí)，算法接近最速下降法。反之，則接近高斯牛頓（Gauss?Newton，G?N）算法，利用二階導(dǎo)數(shù)的信息，快速收斂到最優(yōu)解。

在一定飛行條件和某工作狀態(tài)下分別使用階躍信號(hào)、偽隨機(jī)信號(hào)和混合信號(hào)激勵(lì)部件級(jí)模型，利用L?M 算法對(duì)部件模型的輸入輸出數(shù)據(jù)進(jìn)行動(dòng)態(tài)辨識(shí)，驗(yàn)證激勵(lì)信號(hào)對(duì)于系統(tǒng)辨識(shí)的影響。本文以地面條件為例，nH的誤差大小作為評(píng)價(jià)辨識(shí)效果的好壞，結(jié)果分別見(jiàn)表1 和圖3～7，其中，圖3、5、7 中兩條曲線(xiàn)分別代表部件級(jí)模型的輸出轉(zhuǎn)速和辨識(shí)結(jié)果的輸出轉(zhuǎn)速曲線(xiàn)。圖4 為偽隨機(jī)信號(hào)激勵(lì)下辨識(shí)模型與部件級(jí)模型階躍響應(yīng)曲線(xiàn)。圖6為混合信號(hào)激勵(lì)下辨識(shí)模型與部件級(jí)模型階躍響應(yīng)誤差曲線(xiàn)。

圖3 偽隨機(jī)信號(hào)激勵(lì)下的系統(tǒng)辨識(shí)結(jié)果Fig.3 System identification results under pseudo random signal excitation

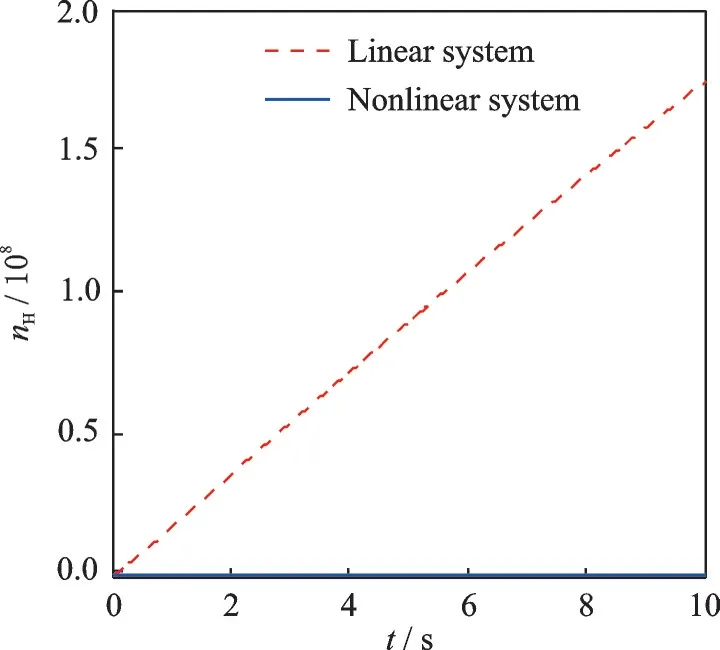
圖4 偽隨機(jī)信號(hào)辨識(shí)結(jié)果的驗(yàn)證Fig.4 Validation of identification results of pseudo random signal systems

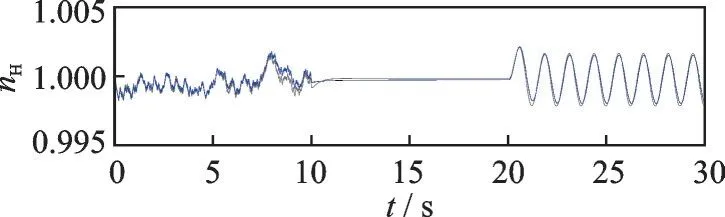
圖5 混合信號(hào)激勵(lì)下的系統(tǒng)辨識(shí)結(jié)果Fig.5 Identification results with mixed signal excitation

圖6 混合信號(hào)激勵(lì)下的系統(tǒng)辨識(shí)誤差Fig.6 System identification error with mixed signal excita?tion

表1 激勵(lì)信號(hào)的辨識(shí)誤差及驗(yàn)證誤差Table 1 Identification error and validation error of exci?tation signal %

圖7 G-N 算法下的系統(tǒng)辨識(shí)結(jié)果Fig.7 System identification results under G-N algorithm

由圖3、4 可知，偽隨機(jī)信號(hào)輸入有很好的動(dòng)態(tài)辨識(shí)效果，但在驗(yàn)證的過(guò)程中，該狀態(tài)空間模型的泛化性能很差，出現(xiàn)發(fā)散現(xiàn)象。

由圖5、6 可知，采用混合信號(hào)輸入的辨識(shí)結(jié)果較好。混合信號(hào)提高了最小二乘的擬合程度，且結(jié)果模型具有較好的泛化能力，在驗(yàn)證過(guò)程中誤差不超過(guò)0.02%。

由圖5、7 可知，求解渦扇發(fā)動(dòng)機(jī)系統(tǒng)辨識(shí)最小二乘問(wèn)題，采用L?M 估計(jì)方法的平均誤差為0.01%，采用G?N 算法得到的最優(yōu)值的平均誤差為0.55%。因此，采用L?M 估計(jì)方法求解的精度更高。

3.2 典型工作點(diǎn)的多項(xiàng)式模型驗(yàn)證

通過(guò)混合信號(hào)與L?M 算法系統(tǒng)辨識(shí)得到地面條件下20 個(gè)工作狀態(tài)的線(xiàn)性系統(tǒng)，通過(guò)多項(xiàng)式擬合建立地面條件下的多項(xiàng)式非線(xiàn)性系統(tǒng)為

非線(xiàn)性系統(tǒng)（15）的矩陣參數(shù)擬合結(jié)果如圖8～11 所示（篇幅有限，僅列出A(x)擬合結(jié)果）。

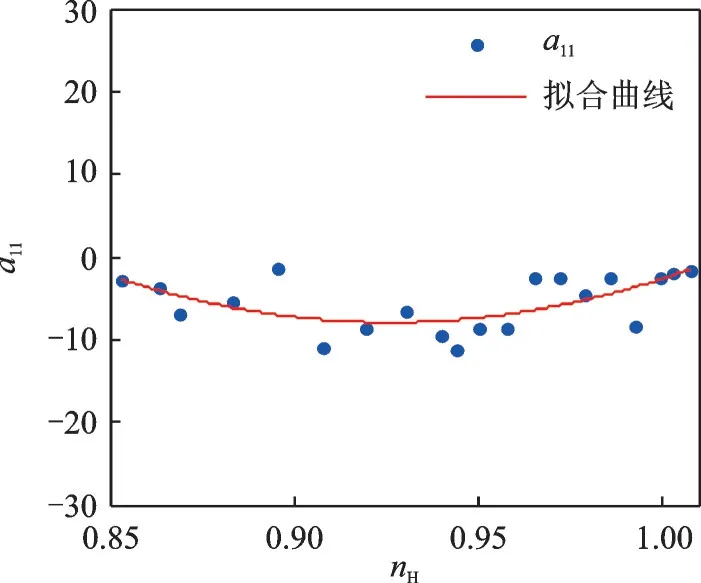
圖8 系數(shù)a11 擬合曲線(xiàn)Fig.8 Fitting curve of a11

為了檢驗(yàn)多項(xiàng)式非線(xiàn)性系統(tǒng)的精度，將其與非線(xiàn)性動(dòng)態(tài)熱力學(xué)模型［19］分別做較大范圍仿真驗(yàn)證，仿真結(jié)果如圖12、13 所示。

由圖12、13 可知，本文建立的多項(xiàng)式非線(xiàn)性系統(tǒng)能夠較精確地反映原系統(tǒng)動(dòng)態(tài)特性，且穩(wěn)態(tài)誤差在0.5%以?xún)?nèi)。由于篇幅有限，未列出其他飛行條件下的多項(xiàng)式非線(xiàn)性模型。

圖9 系數(shù)a12 擬合曲線(xiàn)Fig.9 Fitting curve of a12

圖10 系數(shù)a21 擬合曲線(xiàn)Fig.10 Fitting curve of a21

圖12 nH=0.89 至nH=0.95 仿真驗(yàn)證Fig.12 Simulation verification from nH=0.89 to nH=0.95

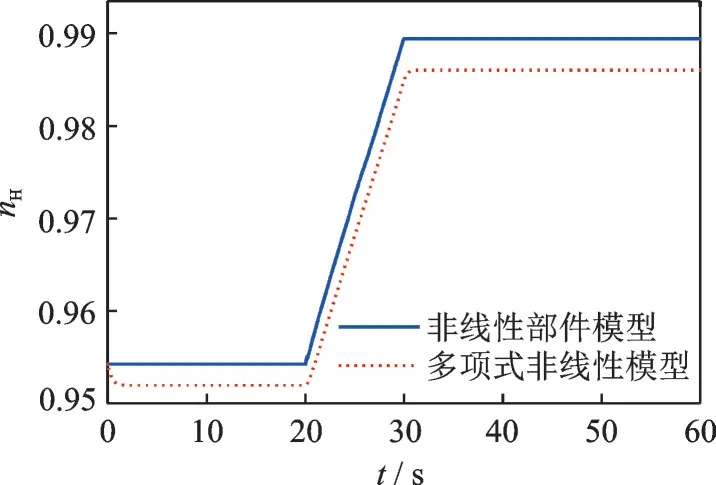
圖13 nH=0.95 至nH=0.99 仿真驗(yàn)證Fig.13 Simulation verification from nH=0.95 to nH=0.99

3.3 大包線(xiàn)NPV 模型驗(yàn)證

本部分將各飛行條件（表2）的模型通過(guò)回歸算法得到大包線(xiàn)NPV 模型如式（16）所示。

表2 大包線(xiàn)H 和MaTable 2 Large envelope H and Ma

式中aij，bij，cij和d2j（i，j=1，2）分別為

為了檢驗(yàn)NPV 模型的精度，將NPV 系統(tǒng)與非線(xiàn)性動(dòng)態(tài)熱力學(xué)模型做仿真驗(yàn)證，仿真結(jié)果如圖14～17 所示。

由圖14～17 可知，NPV 系統(tǒng)與非線(xiàn)性動(dòng)態(tài)熱力學(xué)模型誤差較小，不超過(guò)1%。

圖14 Ma=0.3,H =3 時(shí)nH=0.91～1.04 仿真驗(yàn)證Fig.14 Simulation verification of nH=0.91—1.04 with Ma=0.3,H =3

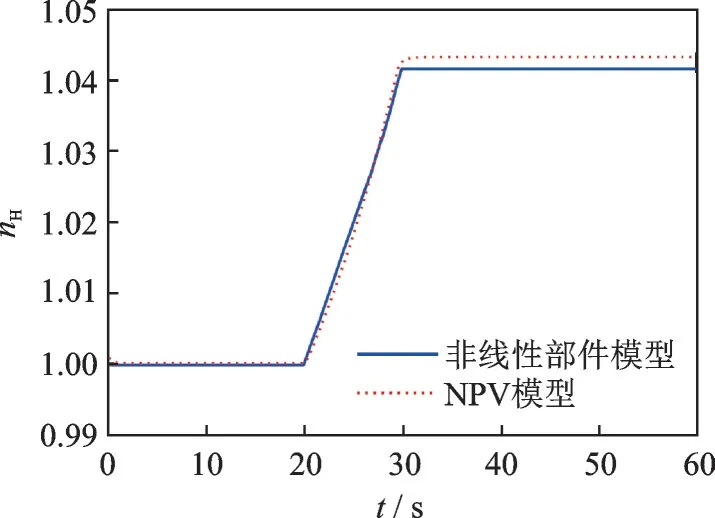
圖15 Ma=1.2,H =8 時(shí)nH=1.0～1.044 仿真驗(yàn)證Fig.15 Simulation verification of nH=1.0—1.044 with Ma=1.2,H =8

圖16 Ma=0.7,H =6 時(shí)nH=0.973～1.039 仿真驗(yàn)證Fig.16 Simulation verification of nH=0.973—1.039 with Ma=0.7,H =6

圖17 Ma=0.2,H =2 時(shí)nH=0.881～0.946 仿真驗(yàn)證Fig.17 Simulation verification of nH=0.881—0.946 with Ma=0.2,H =2

4 結(jié) 論

本文將一種混合信號(hào)作為激勵(lì)信號(hào)，采用L?M 算法求解最小二乘問(wèn)題，采用系統(tǒng)辨識(shí)方法，建立了渦扇發(fā)動(dòng)機(jī)NPV 模型。NPV 系統(tǒng)矩陣參數(shù)能夠根據(jù)高度、馬赫數(shù)以及高壓轉(zhuǎn)子轉(zhuǎn)速實(shí)時(shí)改變，能更好地刻畫(huà)渦扇發(fā)動(dòng)機(jī)的強(qiáng)非線(xiàn)性、時(shí)變特性以及大轉(zhuǎn)速范圍的動(dòng)態(tài)特性，為渦扇發(fā)動(dòng)機(jī)的控制設(shè)計(jì)提供了一種新途徑，是進(jìn)一步研究渦扇發(fā)動(dòng)機(jī)穩(wěn)態(tài)及過(guò)渡態(tài)控制的基礎(chǔ)。在該NPV 建模方法的基礎(chǔ)上，下一步將開(kāi)展增量形式NPV 模型建模研究。