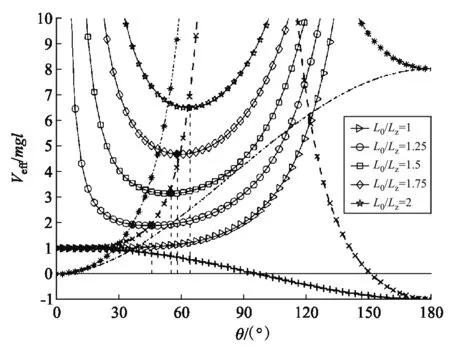
拉格朗日陀螺轉動的有效勢能和可視化
周群益,周麗麗,莫云飛,侯兆陽
(1.廣州理工學院通識教育學院,廣東 廣州 510540;2.贛南醫學院 醫院信息工程學院,江西 贛州 341000;3.長沙學院 電子信息與電氣工程學院,湖南 長沙 410022;4.長安大學 理學院應用物理系,陜西 西安 710064)
在重力場中定點轉動的對稱陀螺又稱為拉格朗日陀螺.劉賢雨同學根據柯尼西定理列出了陀螺的動能公式,形成了拉格朗日函數,推導了3個運動積分,進而得出了機械能守恒公式和有效勢能公式[1].論文中的機械能守恒公式和有效勢能的公式與國內有關教材中的公式都不相同,曲線不能直觀地說明有效勢能變化規律和陀螺運動的穩定性.本文根據剛體的運動學方程和陀螺運動的動力學方程重新推導了有效勢能的公式,繪制了有效勢能的曲線族,說明了陀螺運動的類型和穩定性.
1 拉格朗日陀螺的機械能守恒定律
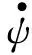

圖1 剛體轉動的3個歐拉角和角速度的方向
在活動坐標系Oxyz中,陀螺的角速度為
ω=ωxi+ωyj+ωzk
(1)
利用角度關系可得
(2)
這就是歐拉運動學方程.歐拉動力學方程為
(3)
其中,Mx,My和Mz是外力矩的三個分量.
質心C對支點O的位矢為
rC=lk
(4)
其中k是Oz軸的單位矢量.在固定坐標系OXYZ中,OZ方向的單位矢量為K,用動坐標系的單位矢量和歐拉角可表示為
K=sinθsinψi+sinθcosψj+cosθk
(5)
重力可表示為
FG=-mgK=-mg(sinθsinψi+sinθcosψj+cosθk)
(6)
重力對支點的力矩為
M=rC×G=mgl(sinθsinψi-sinθcosψj)
(7)
陀螺的動力學方程為
(8)
對方程組求解,可得出一些重要結果:
1) 對式(8)的第三式積分可得
J3ωz=Lz(常量)
(9)
其中,積分常量Lz是角動量L在Oz方向的投影.這是Oz方向角動量守恒公式.由于陀螺繞Oz軸的轉動慣量為J3,角速度為ωz,Lz就是繞Oz軸的角動量.由于J3是常量,所以角速度ωz也是常量.
2) 由式(8)的前兩式可得
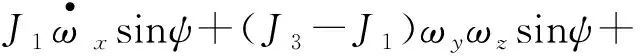
多次利用式(2),經過比較復雜的推導可得
積分可得
J1ωxsinψsinθ+J1ωycosψsinθ+J3ωzcosθ=L0
(10)
其中,積分常量L0是角動量L在OZ方向的投影.這是OZ方向角動量守恒公式.
3) 由式(8)的前兩式可得
將式(2)的前兩式代入上式可得
即
J1ωxdωx+J1ωydωy-mglsinθdθ=0
積分可得
(11)
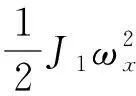
(12)
其中,E也是能量常數:
(13)
如果將E當作陀螺的全部能量,那么E0就是部分能量,在下面的討論中只需要利用部分能量就行了.
有些教材根據角動量守恒定律推導了公式(9)和(10)[2-4],有些教材利用拉格朗日函數推導了公式(9)和(10)[5-6].這些教材都根據機械能守恒定律得到了式(12).
將式(2)的前兩式代入式(12),可得
(14)
將式(2)的前兩式代入式(10),可得
(15)
將上式代入式(14),可得能量守恒公式:
(16)
文獻[1]用拉格朗日函數求出兩個角動量守恒公式,再列出機械能守恒公式(14),用本文的符號表示如下:
2 拉格朗日陀螺的有效勢能
由于文獻[1]中的式(14)的錯誤,得出的有效勢能公式也是錯誤的:
由式(16)可得正確的有效勢能公式
(17)
對有效勢能求導數,可得
(18)
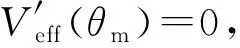
有效勢能的二階導數為
mglcosθ
(19)
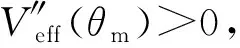
在有效勢能的公式中,m、l和J1是常數,L0和Lz是可調節的參數,參數決定了陀螺的運動狀態.
2.1 當Lz=0時的有效勢能
當Lz= 0時,必有ωz= 0,由式(17)可化簡有效勢能
(20)
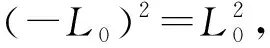
(21)
由式(19)可化簡其二階導數:
(22)
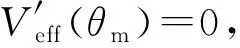
(23)
顯然π/2 <θm≤π.將上式代入式(22)可得
(24)
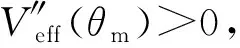
(25)
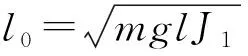
(26)
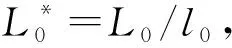
(27)
由式(24)可得平衡角無量綱的二階導數
(28)
將公式無量綱化便于應用MATLAB畫曲線和曲線族,從曲線中解讀隱含的信息[7].
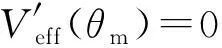
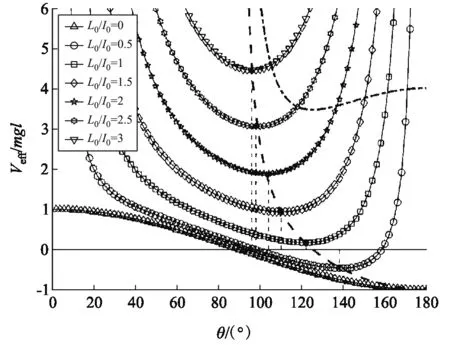
圖2 陀螺在Lz = 0時的有效勢能
2.2 當Lz = -L0時的有效勢能
當Lz= -L0≠ 0時,由式(17)可化簡有效勢能
(29)
由式(18)可化簡其導數,
(30)
由式(19)可化簡其二階導數,
(31)
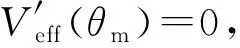
(32)
說明θm=π是穩定的平衡角.
很容易將有效勢能和它的導數以及二階導數無量綱化.
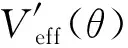
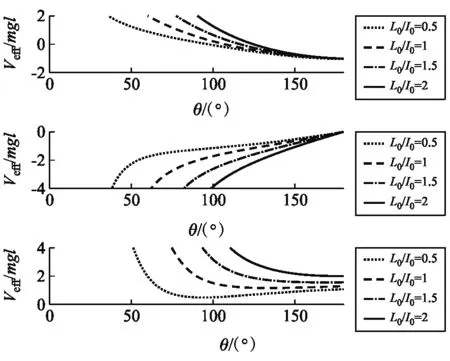
圖3 陀螺在Lz = -L0時的有效勢能和導數以及二階導數
2.3 當Lz = L0時的有效勢能
當Lz=L0≠0時,由式(17)可化簡有效勢能
(33)
由式(18)可化簡其導數
(34)
由式(19)可化簡其二階導數
(35)
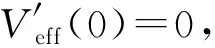
(36)
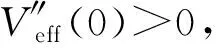
(37)
對上式再求導數,
(38)
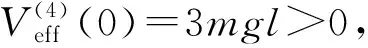
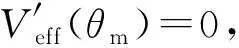
(39)
在L0< 2l0的情況下,還有一個平衡角:
(40)
將式(39)代入式(35),可得
(41)
說明θm是有效勢能的極小點,因此θm是穩定的平衡角.可見:當Lz=L0時,如果L0< 2l0,即:陀螺轉得不夠快,就不能倒立在支點上旋轉,而只能以不為零的章動角θm旋轉.將式(39)代入式(33),可得平衡角的有效勢能:
(42)
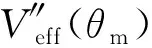
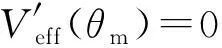
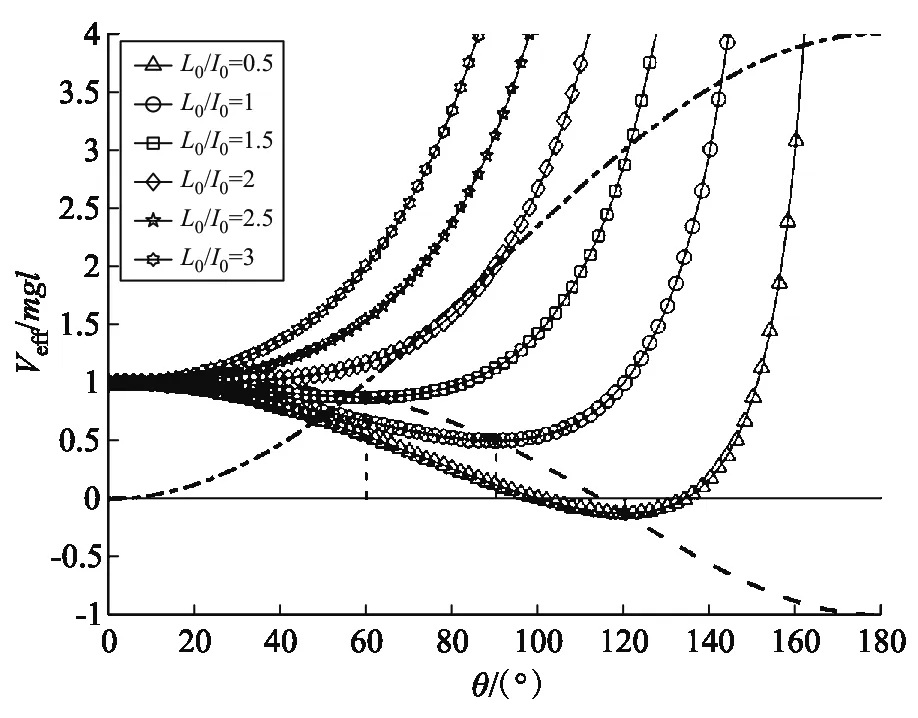
圖4 陀螺在Lz = L0時的有效勢能
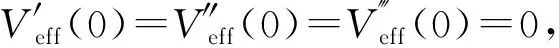
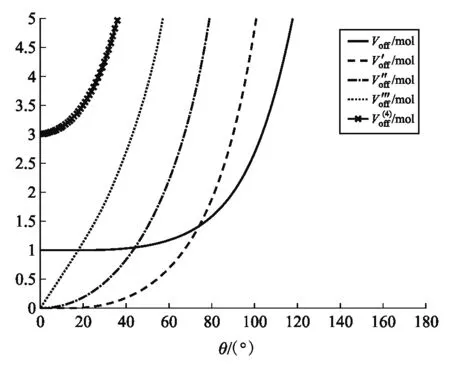
圖5 陀螺在Lz = L0 = 2l0時的有效勢能和各階導數
2.4 一般情況下的有效勢能
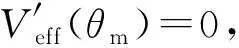
(43)
其中
(44)
當θm=π時,則a= -1,b= -2Lz,c= -Lz2,由式(43)解得L0= -Lz.當θm= 0時,則a= 1,b= -2Lz,c=Lz2,由式(43)解得L0=Lz.當0 <θm<π時,根的判別式為
(45)
其中,D是更簡單的根的判別式:
(46)
假設D≥ 0,由式(43)解得
(47)
這是角動量L0與Lz和θm之間的關系.當Lz一定時,如果D> 0,在0 <θm<π范圍內,除了θm=π/2之外,同一個θm對應著兩個值L0.將上式代入式(17),可得θm處的有效勢能:
(48)
當θm→π-時,Veff(θm)→-mgl=Veff(π);當θm→0+時,Veff(θm)→mgl=Veff(0).如果式(48)取正號,當θm→π/2時,Veff(θm)→+∞,θm= π/2是無窮間斷點.如果式(48)取負號,可以證明:
(49)
因此,θm=π/2是可去間斷點.
將式(47)代入式(19),可得平衡角θm的二階導數:
(50)
注意:當θm→π-時,由式(47)可得L0→-Lz,由上式可得
(51)
(52)
因此,θm= 0處的穩定性應該由式(36)判斷,也可以由上式判斷.
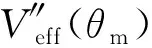
(53)
因此,θm= π/2是可去間斷點.由于這個極限大于零,所以θm= π/2是穩定的平衡角.
無量綱的有效勢能為
(54)
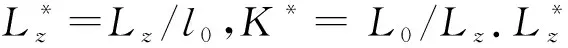
(55)
無量綱的二階導數為
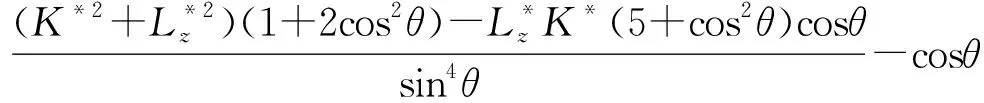
(56)
平衡角無量綱的有效勢能為
(57)
其中,無量綱的根的判別式為
(58)
平衡角無量綱的二階導數為
(59)
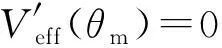
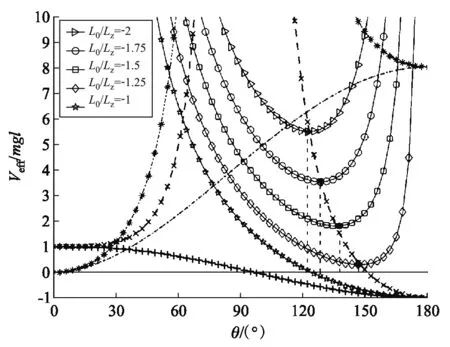
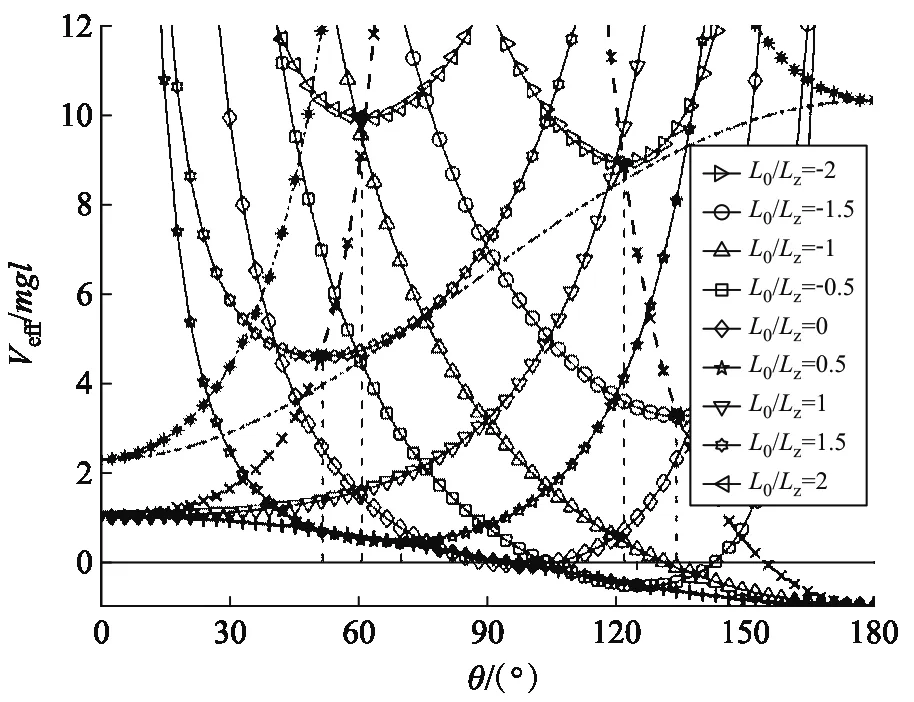
圖6 陀螺在Lz = 2l0時的有效勢能(L0 ≤ -Lz)
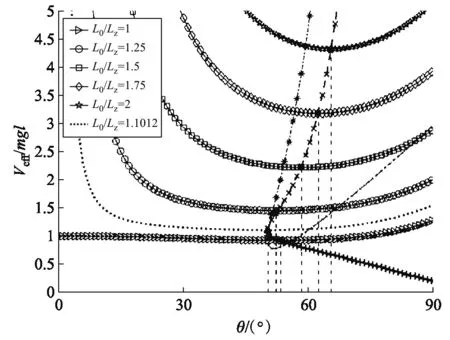
如圖7所示,當-Lz 圖7 陀螺在Lz = 2l0時的有效勢能(-Lz ≤ L0 ≤ Lz) 如圖8所示,當L0>Lz時,Veff(θ)還是先降后升的曲線族,但是極小值分布在上支左段上;L0越大,Veff(θm)就越大.當L0=Lz時,Veff(θ)是單調上升的曲線,極小值位于Veff(θm)的上支左段和下支的交點上(0,mgl).可見:θm的穩定分布區域為[0,π/2],陀螺質心只能在上半球面做規則進動. 圖8 陀螺在Lz = 2l0時的有效勢能(L0 ≥ Lz) 圖9 陀螺在Lz = 2.4l0時的有效勢能 當E0=Veff(θm)時,陀螺做規則進動,對同一個θm,上支的E0較大,表示快規則進動,下支的E0較小,表示慢規則進動. 3) 當Lz< 2l0時,令D= 0,可得臨界穩定角θmC與角動量Lz的關系: (60) 顯然,0 ≤θmC≤π/2.θmC是下支與上支左段相交時穩定的章動角.利用上式,式(47)可化為 (61) 這是臨界條件下兩個角動量之間的關系.當D= 0時,由式(48)可得臨界有效勢能 (62) 由式(50)可得臨界有效勢能的二階導數 (63) 將公式無量綱化即可繪制曲線. 圖10 陀螺在Lz = 1.6l0時的有效勢能(L0 ≥ Lz) 當0 利用有效勢能,可以求章動角的周期,還可以求章動角受微擾的周期.如果設u= cosθ,就可以將式(16)化為u的微分方程,引入橢圓積分就能求出θ(t)的表達式,進而求出兩個周期的表達式.本文受篇幅所限,無法詳述. 本文求出推導了陀螺運動的有效勢能公式和導數公式,將公式無量綱化,應用MATLAB畫出曲線和曲線族,詳細地說明了陀螺運動的穩定性.劉賢雨同學作為00后的本科生,分析了陀螺在重力場中轉動的類型,展現了本科生科研能力和創新能力.MATLAB是一種計算和繪圖功能都十分強大的工具,可以推導和驗證公式,還能展現問題的每個細節.MATLAB不但能夠研究陀螺的有效勢能,還能精確地計算章動角的變化范圍和周期以及運動規律,精密繪制陀螺質心的軌跡.如果本科生掌握了這種工具,將如虎添翼,大大提高大學生提出問題和解決問題的能力.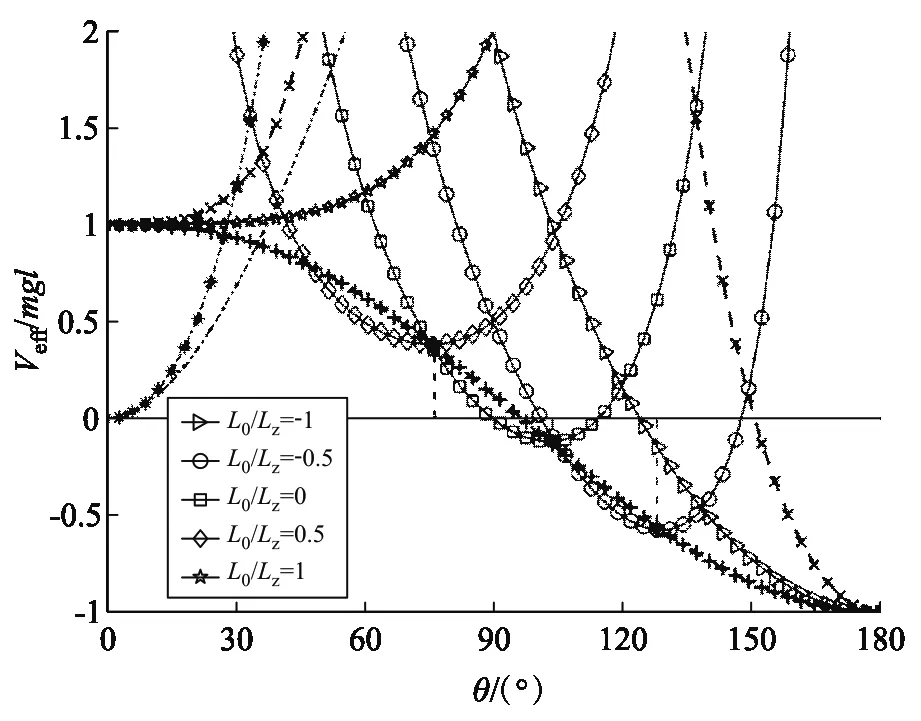
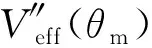
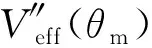
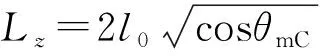
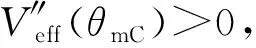
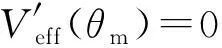
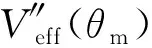
3 結論

