基于Shapley值分解的高職學院生均經費支出省際差異研究
邱向英
(湖南環境生物職業技術學院,湖南 衡陽 421005)
0 引言
縱觀我國教育產業改革發展的數十年可知,高職教育經費投入歷經了巨大的變更,在教育市場改革開放的初期,大部分學院生支出經費由政府進行統一支出,在后期的持續發展與改革中,教育市場將經費管理權下放,相關經費的管理權利便呈現一種分散狀態[1]。在我國對高職院校教育工作給予了足夠的重視與關注后,高職院校學院生均經費支出開始遞增,但在深入對市場調查后發現,不同省市之間的差異是仍然存在的,這種差異不僅導致了各省市教育水平發展不均衡,同時也在一定程度上導致了教育產業建設的不公正。而相關縮小高職學院生均經費支出省際差異的研究,已成了教育產業與各省市政府密切關注的問題[2]。在參與市場調研中,部分研究學者認為,應當將高職教育定義為一種公共類型產品,并認為該教育的可持續發展可以提高社會勞動力的增長率,并在一定程度上帶動產業的發展。并且,在現如今教育市場內,高職院校無論是從數量層面分析,或是從教學規模入手,均承擔著優化教育產業結構的重要責任,因此,結合市場需求,適當加大對教育的投資也是十分有必要的。為了實現教育市場內各個省市的均衡發展,該文將基于Shapley值分解視角,設計一種針對高職學院生均經費支出的省際差異分析方法,促進我國教育教學工作的持續完善。
1 基于Shapley值分解的高職學院生均經費支出省際差異分析方法設計
1.1 高職學院生均經費支出省際差異指數計算
為實現對高職學院生均經費支出省際差異的量化分析,該文首先針對其差異指數進行計算,為了方便論述,該文以部分地區在近5年高職學院生均經費支出情況為依據,對其進行省際差異指數計算。表1為近5年部分省域高職學院生均經費支出表。
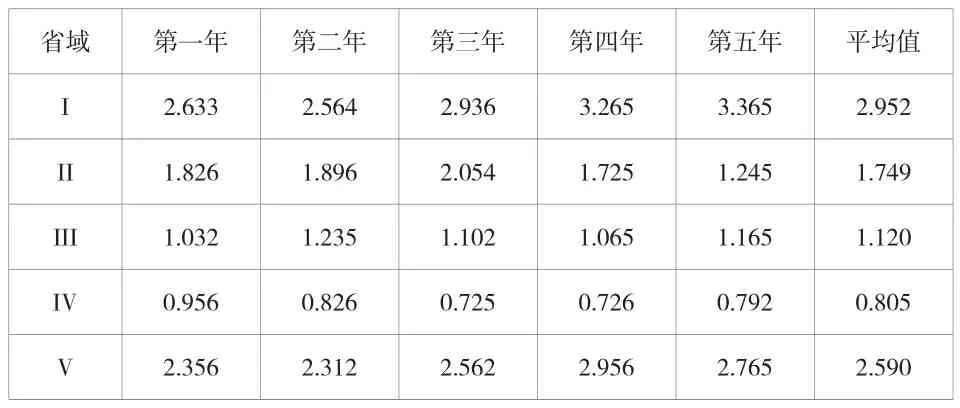
表1 各省域高職學院生均經費支出表(單位:萬元)
從表1中的數據可以看出,各省域高職院校的教育財力資源增幅均存在明顯差異,但近5年來各地區的高職學院生均經費支出均呈現出負增長的趨勢,這一現象反映了高職院校的教育財力資源在面對大規模擴招的市場發展變化中準備并不充分。
在上述背景下,為更加精確地對高職學院生均經費支出省際差異及其變化進行表達,引入基尼系數、對數偏差均值指數,對表1中的數據作進一步分析。基尼系數如公式(1)所示。

式中:G為基尼系數;xi為在某一省域i中高職學院生均經費支出;xj為在某一省域j中高職學院生均經費支出;k為所有被分析省域高職學院數量;u為以高職學院在校人數作為權重的所有省域中高職學院生均經費支出的加權平均值。
對數偏差均值指數的計算如公式(2)所示。

式中:M為對數偏差均值指數;pi為某一省域i中高職學院在校生數量占所有高職學院在校生人數的比重。
根據上述公式(1)和公式(2),對高職學院生均經費支出省際差異指數進行計算。通常情況下,基尼系數G對上層和低層發展水平的變化更加敏感,而數偏差均值指數M對中間層發展水平的變化更加敏感。結合表1中的數據,得出其相應的G值和M值并記錄,如表2所示。
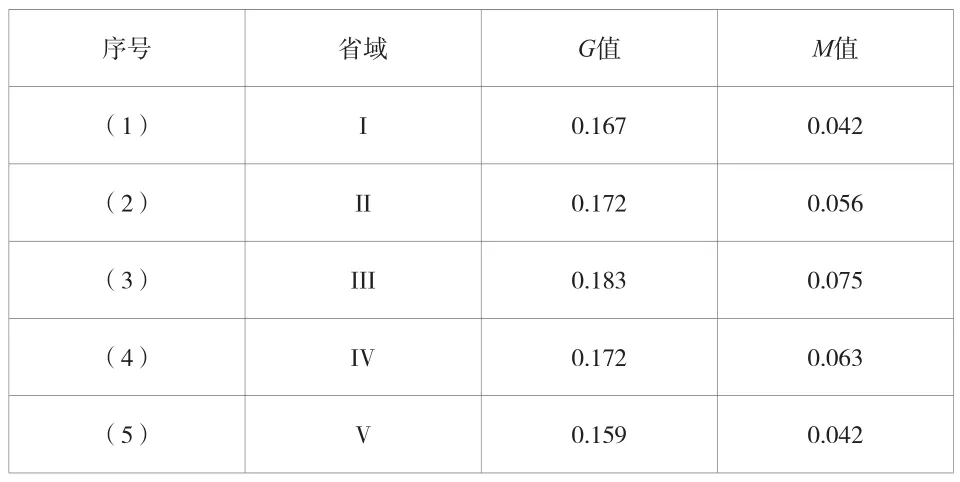
表2 各省域高職學院生均經費支出對應指數
在獲得相應的G值和M值后,根據數據在每年的變化情況,能夠為后續差異分析提供更加準確的數據條件。例如表2中,G值和M值均隨著年份的增加呈現出現增加后降低的趨勢,其轉折點均出現在第三年,說明在第三年前后高職學院生均經費不均衡程度增加,以此完成對高職學院生均經費支出省際差異指數計算。
1.2 明確高職學院生均經費支出省際差異影響因素
在完成上述相關研究后,可知現如今高校學生的人均教育支出存在不平等指數差異,因此,可通過將差異值代入因變量回歸方程,進行統計結果的綜合分析[3]。在該過程中,通過市場調查與走訪各大高校實地調研的方式,選擇高校大學生人數、政府對教育投資的意愿、教育行為傾斜度、政府現有固定資產、高校創新教育能力等作為分析差異的影響因素,并要求選定的因素指標之間均具有不可代替性與不可對抗性,在上述選定的指標中,政府對教育投資的意愿將直接決定高校教育經費支出的能力,可將該項指標作為此次研究的切入點,構建1個半對數面板數據參照模型,選定該模型進行分析的原因主要是在進行因變量的取值后,其原始值將呈現一種趨近于變量值的正態分布方式,并且在使用此模型進行對數取值后,可以通過方程的轉化實現對常數項的規避,從而避免分析結果與實際結果之間出現較大的誤差[4]。對半對數面板數據參照模型的描述,如公式(3)所示。
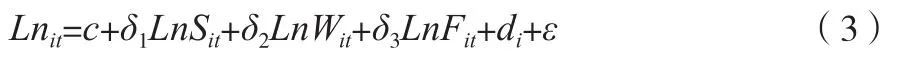
式中:Lnit為對半對數面板數據參照模型,其中i與t分別表示為對省市與年份;c為教育產業社會發展的固定效應;δ1為政府對教育投資的意愿;δ2為教育行為傾斜度;δ3為政府現有固定資產;Sit為隨機效應;Wit為市場效應;Fit為預期效應;di為虛擬變量;ε為分析過程中的擾動項目。
在掌握影響高職學院生均經費支出省際差異的相關因素后,采用回歸計算的方式,對上述提出的各項因素進行解釋度計算,當計算結果可通過1%顯示時,證明該項指標對經費支出省際差異存在影響,且該項影響是積極的,反之,可認為該項指標對前者不存在影響或無顯著干擾作用[5]。以該方式完成對高職學院生均經費支出省際差異影響因素的提取,實現對課題內容的分析。
1.3 基于Shapley值的省際差異分解
在上述高職學院生均經費支出省際差異指數的基礎上,引入Shapley值,利用G值和M值可對影響其差異的線性組合進行表示,再利用Shapley值可以進一步將其轉換為能夠解決一般分解問題的方法。對影響高職學院生均經費支出的指標不平等指數I進行計算;再確定該影響指標的決定方程,將某一影響指標的數值X取平均值,將其與其他影響指標數值統一計入方程中并獲取全新的影響指標數值,并再次對其不平等指數進行計算。
此時該數值中已經不再含有X,此時說明高職學院生均經費支出不會受到該影響指標X的影響;最后,計算上述2個影響指標的不平等指數的差值,得出的X即為被分析的影響指標對省際差異作出的貢獻。同時,根據X均值選取影響指標擴大或縮小的判斷[6]。
當取均值后,若兩個影響指標數值差距縮小,則說明該影響指標X是擴大差異的主要因素;若2個影響指標數值差距增加,則說明該影響指標X是縮小差異的主要因素。由于上述計算量較大,為了減輕該文差異分析方法的計算負擔,可將Shapley值對省際差異的分解引入JAVA程序中,按照上述流程完成計算。
除此之外,還可利用不同影響指標的貢獻度對高職學院生均經費支出省際差異進行進一步地分解。在分解前,首先需要通過上述公式(3)中不同影響指標,確定高職學院生均經費支出省際差異的關聯程度,以此確保與影響指標解釋的差異部分越多越好。
當上述得出的G值、M值在所有影響指標中的貢獻度排序呈現出高度一致的情況時,則說明通過Shapley值對高職學院生均經費支出省際差異的分解具有內在穩定性。因此,根據貢獻程度,不僅分析影響指標,同時還能夠驗證不同影響指標選擇是否正確。
以某省域為例,若該省域中固有影響指標和省域政府教育的投入意愿在分析考察期間內對高職學院生均經費支出省際差異的相對貢獻度為負數,則說明該影響指標為縮小差異性的力量。除此之外,部分影響指標還存在一定的特殊性,通過各個省域特有的影響指標能夠充分反應該區域高職學院教學資源稟賦以及長期政府政策的傾斜。對部分地區而言,由于政府的長期傾斜,因此高職學院教育財力資源存在失衡問題,該指標的投入能夠促進其協調發展。
傳統方法通常會采用殘差項對其他未考慮的影響指標進行表示,并將其殘差的影響理想化為零。但在實際應用于對高職學院生均經費支出省際差異的分析時,殘差不會存在為零的情況,并且無論其結果是正數還是負數,都表明高職學院生均經費支出情況在省際間對比存在差異[7]。
因此針對該問題,在確定以公式(3)作為回歸方程后,將固定效應的截面虛擬為影響指標,并將其視為某一省域內特有的影響指標,通過該指標實現對省域資源稟賦、歷史發展滯后效應等內容的精準描述。在Shapley值分解的過程中,特定的影響指標對高職學院生均經費支出省際差異貢獻的同時,其本身的變化主要受到影響指標自身分布的均衡性影響,同時與其二者之間的相關度也有一定的聯系。例如當政府教育投入意愿的基尼系數呈現出波動的縮小趨勢時,則可能該影響指標即為造成高職學院生均經費支出省際差異增加的主要原因,同時該影響指標的貢獻程度越高,則造成高職學院生均經費支出省際差異的作用越明顯。通過上述論述,實現對高職學院生均經費支出省際差異的Shapley值分解,并根據上述得出的影響指標對未來不同省域的高職學院生均經費支出情況進行預測。
2 實驗論證分析
2.1 實驗準備
結合上文,完成對差異分析方法的理論設計,為了進一步驗證Shapley值分解在該分析方法中的應用是否能夠優化其得出的分析結果,該文選擇以開始實行高等職業教育和普通專科教育合并的年份起,截至后5年的5個不同省域的高職學院生均經費支出情況作為實驗數據,如表3所示。
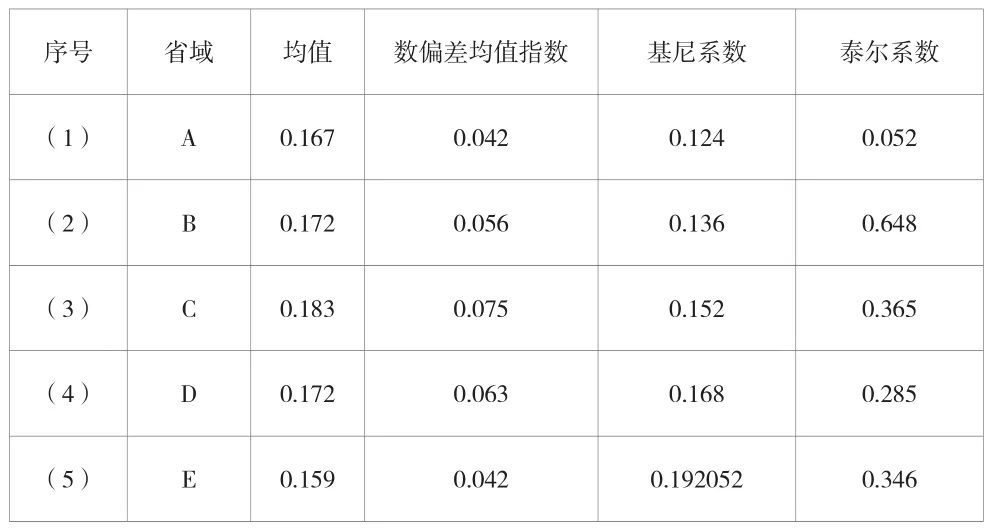
表3 5個不同省域高職學院生均經費支出情況
分別利用該文提出的差異分析方法和傳統基于Theil的差異分析方法對上述統計數據進行分析,表3中包括了用于該文基于Shapley值分解的差異分析方法的數偏差均值指數和基尼系數以及用于傳統基于Theil的差異分析方法的均值和泰爾系數。結合表3中的數據,利用2種分析方法得出影響高職學院生均經費支出省際差異的影響指標,并結合分析結果對未來5年內高職學院生均經費支出省際差異變化情況進行預測。將預測結果與實際后續5年的各地區高職學院生均經費支出情況進行對比,以此驗證2種差異分析方法的分析準確性。
2.2 實驗結果及分析
根據上述實驗準備,分別完成2種差異分析方法對高職學院生均經費支出省際差異情況的分析,隨機選擇一個省域內高職學院生均經費支出得出的結果進行記錄,并將2種分析方法得出的未來變化趨勢與實際情況進行對比,得到如圖1所示的實驗結果對比圖。
從圖1中的實驗結果可以看出,在該文差異分析方法與傳統分析方法分析得出的影響指標的基礎上,該文方法預測得出的變化趨勢更加接近于該省域高職學院生均經費支出變化情況。綜上所述,該文結合Shapley值分解設計的差異分析方法在實際應用中能夠得到更加精準的分析結果,并找出更加準確的影響因素,完成對高職學院生均經費支出省際差異未來差異的進一步分析。將該方法應用于實際能夠為制定高職學院生均經費支出制度提供可靠依據。
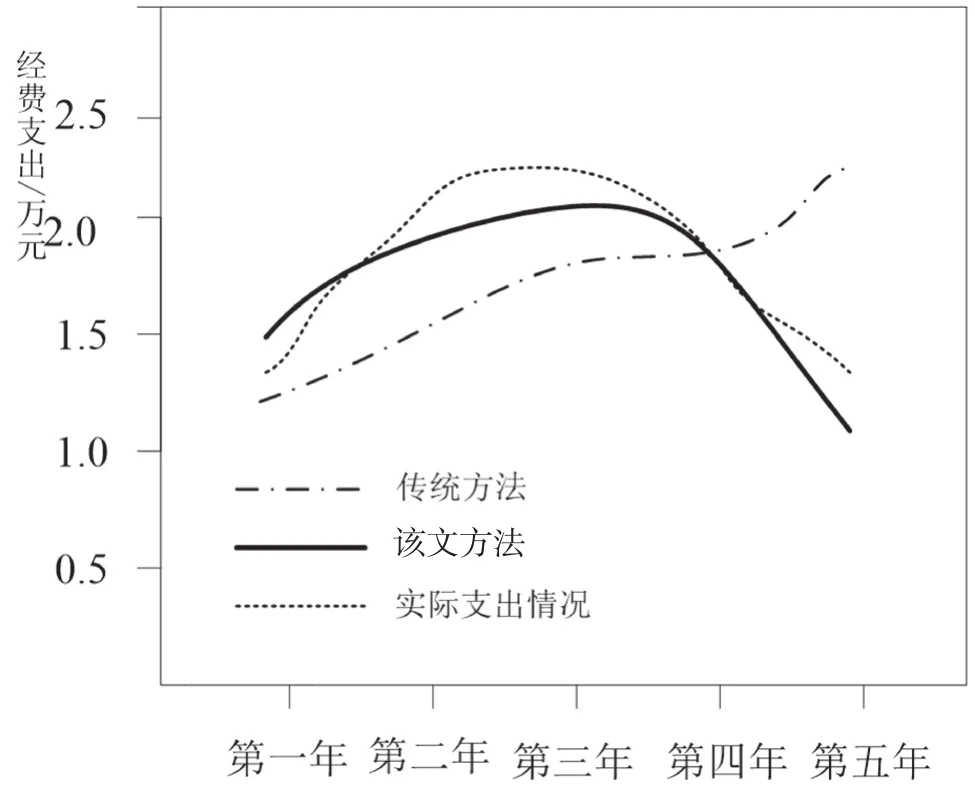
圖1 2種差異分析方法實驗結果對比圖
3 結語
針對當前傳統差異分析方法無法準確找出影響高職學院生均經費支出因素的問題,該文結合Shapley值分解,提出一種全新的差異分析方法,并通過實驗驗證的方式,證明了該方法在實際應用中的優勢。在后續的研究中,為了進一步提高該文差異分析方法的適應性,還將結合更多指數計算方式,對其差異影響因素進行定性和定量分析,從而找出更加準確的影響指標,并基于分析結果建立教育資源空間防控機制,避免出現高職學院教育資源冗余的問題,避免滯后省域的高職學院教育資源被發達省域過渡吸收,提高滯后剩余的教學資源利用率,完善各省域高職學院教育。

