一種基于分子動力學的網格劃分方法

趙曉斌，周素素，李文華，邱偉強，薛鴻祥

(1.上海交通大學 船舶海洋與建筑工程學院，上海 200240；2.中國船舶及海洋工程設計研究院，上海 200011)

0 引言

船體有限元參數化網格劃分方案主要有2 種：1）使用通用軟件在進行必要的約束設置后直接對幾何進行網格劃分，然后手動進行修改以滿足有限元計算的精度需要，如Catia，Napa 等；2）使用通用軟件的二次開發功能，設置硬點和硬線，或者將幾何目標域離散化為細小的、形狀盡可能規則的零件（如肘板的趾端，開孔或者角隅的邊緣），分別對其進行網格劃分，然后拼裝在一起，如在Patran 中使用PCL 程序。

若使用第1 種方法進行參數化網格劃分，可能無法直接滿足有限元計算精度的要求（如開孔邊緣出現三角形等）；如果使用第2 種方法，則需要考慮根據不同的情況(如幾何邊界，內部有無開孔等)制作參數化幾何模型后再劃分單元，稍顯缺乏靈活性。

所以，一個較為折衷的方案是幾何形狀較為規整的位置使用通用軟件進行網格劃分，而在有限元計算較為關注網格質量及需要形狀參數優化的特殊區域，使用自定義網格劃分方法。不失一般性，本文主要研究二維平面多連通域的網格劃分方法，坐標變換后可適用于三維空間平面的情況。

對于目標域的四邊形網格劃分，目前商業軟件主要使用映射法和鋪砌法。映射法算法效率高，網格質量好，但是僅適用于簡單的規則區域。而鋪砌法的適用范圍較廣，可用于劃分復雜不規則區域或多連通區域，網格質量一般較好，邊界網格形態規則，不規則節點較少，但是交叉判斷和實現算法較為復雜[4]。

為實現多連通域的網格劃分，同時避免算法的復雜性，本文使用分子動力學的方法控制目標域內節點之間的相互距離和相互位置關系，并由此嘗試控制目標域內的網格形狀和網格質量。

1 帶電粒子的分子動力學模擬

分子動力學（MD）是研究復雜物理和化學系統的常規建模工具，其核心類似于計算機圖形學中的粒子系統[5]。“粒子”是分子動力學的基本模擬單元，可以表示物理世界中的原子、分子、離子等。在實踐中，它被編碼為具有位置、速度、加速度和其他物理屬性（如電荷）的質量點。

1.1 理論模型

在粒子系統中，若假設粒子的質量為單位質量1，則任意粒子i的動力學方程為：

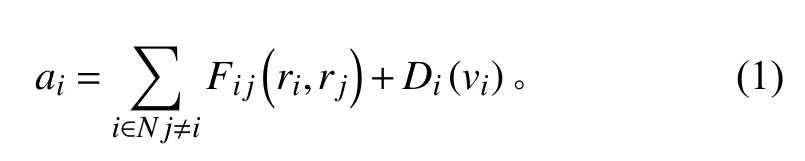
式中：ai，vi，ri分別為粒子i的加速度、速度和位移；粒子j為粒子i的相鄰粒子；Fij為粒子i與粒子j之間作用于粒子i的相互間作用力；Di為粒子i在運動過程中受到的阻力。

如用分子間相互作用勢函數表示分子間的相互作用，則勢函數V與分子間相互作用力函數Fij間的關系為：

式中：勢函數V可表示為

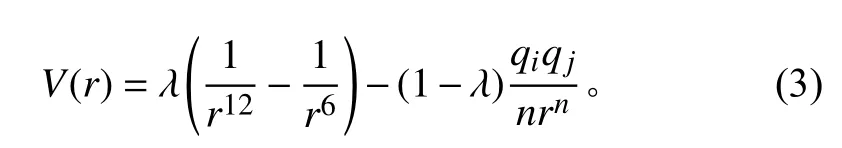
其中：

式中：r為粒子間的相對距離；σ 為網格劃分大小；qi為粒子的電量，大于0 帶正電荷，小于0 則帶負電荷。

式（3）中的第一項為Lennard-Jones 勢函數。Lennard-Jones 勢函數隨粒子間距的變化如圖1 所示。

由勢函數表達式及圖1 可見，當粒子間距無窮遠時，粒子間產生的相互吸引作用非常微弱，無限接近于0；當它們相互靠近時，粒子間產生相互吸引力逐漸增加；當粒子間的相對位置r=1 時，Lennard-Jones 勢為0，吸引力消失。這時，如果2 個粒子繼續靠近，它們之間將相互排斥，且粒子間的排斥力隨粒子間距離的減小而迅速增大。Lennard-Jones 勢與帶電粒子的正負號無關。

圖1 Lennard-Jones 勢函數隨粒子間距變化Fig.1 Trend of the Lennard-Jones potential function varies with spacing of the particles

式（3）中的第二項為庫倫勢函數。帶電粒子間的庫倫力作用與帶電粒子的正負號相關，符號相同的電荷相互排斥，符號相反的電荷相互吸引。自然界中式（3）中的n取值為1，當n取值不為1 時，將會影響庫倫力的作用范圍，從而對數值計算產生影響。

1.2 短程庫倫力

當式（3）中的庫倫勢函數參數n取1 時，庫倫勢與粒子間距離的一次方成正比，是一種長程相互作用，不能使用計算近程相互作用時常用的截斷近似。這使得計算次數是O（N2）的數量級，其中N是粒子的數量。而式（3）中的Lennard-Jones 勢函數隨距離的增加衰減的很快，是一種短程作用，計算次數是O（N）的數量級。

為了減少計算量，令式（3）中n=5，此時當r=2.5 時，即粒子間的距離在網格劃分大小的2.5 倍左右時，庫倫勢衰減為r=1 時的1%左右。當粒子間的距離大于2.5 倍網格劃分大小時，庫倫勢的作用可以忽略不計。

另一方面，電荷符號相反的粒子在距離很小時會產生很大的吸引力，而距離很接近的粒子之間也會由于Lennard-Jones 勢產生較大的斥力，為了避免粒子產生較大的加速度從而飛出網格劃分區域，所以當粒子間的距離小于0.2σ時，仍然取r=0.2。

1.3 勢函數權重因子

Lennard-Jones 勢和庫倫勢在粒子運動過程中的作用有所不同。Lennard-Jones 勢用于控制粒子間的相對距離在預定的網格劃分距離σ附近，而庫倫勢由于粒子的正負電荷不同，使得粒子在電場作用下位置發生偏移。

為了說明Lennard-Jones 勢和庫倫勢在分子運動過程中起到的作用，在一個正方形區域內設置若干等量正負電荷的粒子，正方形區域邊界也由正負電荷粒子交替圍成防止內部粒子逃逸出區域。粒子的初始狀態如圖2 所示。

圖2 粒子間分布初始狀態Fig.2 Initial state of the particle distribution

調整式（3）中的λ值分別為：0，即僅有庫倫勢作用；1，即僅有Lennard-Jones 勢作用；0.5，即在Lennard-Jones 勢和庫倫勢的共同作用下。3 種情況下區域內粒子的分布如圖3～圖5 所示。不難發現，當僅有庫倫勢作用時，粒子分布無規則，甚至有一部分粒子逃逸出矩形區域；僅有Lennard-Jones 勢作用時，粒子之間保持一定的相對距離，卻無法維持初始的四邊形分布狀態；當Lennard-Jones 勢和庫倫勢的共同作用時，粒子維持了初始的四邊形分布狀態。

圖3 λ=0，僅有庫倫勢作用粒子間分布Fig.3 Distribution of particles under coulomb interactions only

圖4 λ=1，僅有Lennard-Jones 勢作用粒子間分布Fig.4 Distribution of particles under Lennard-Jones potentials only

圖5 λ=0.5，Lennard-Jones 勢和庫倫勢的共同作用下粒子間分布Fig.5 Distribution of particles under coulomb interactions and Lennard-Jones potentials

1.4 阻尼

由于粒子在運動到平衡位置后會開始作往復振動，若不設置阻尼，粒子將一直運動下去，所以使用下式模擬式（1）中的阻尼項Di(vi)：

式（5）中阻尼系數μ取值大則加快粒子運動的收斂，但是取值過大可能妨礙粒子的正常運動。當粒子運動軌跡相似時，可以考慮使用較大的阻尼加快收斂速度。

1.5 數值積分

常見的數值積分方法包括Velocity-Verlet 法[1]，龍格-庫塔（Runge-Kutta）法[6]以及歐拉法。

Velocity-Verlet 法更新粒子的位置和速度到下一個時間步長只需要進行一次評估，截斷誤差為O（h4）（h是步長）。相較而言，四階龍格-庫塔（Runge-Kutta）法雖然截斷誤差是O（h5）（h是步長），可是其計算量卻大于Velocity-Verlet 法。而歐拉法雖然簡單，但是其精度相對較差。

所以，綜合計算精度和計算速度，本文采用Velocity-Verlet 法進行數值積分。Velocity-Verlet 法計算粒子的位置和速度可以用下式表示：

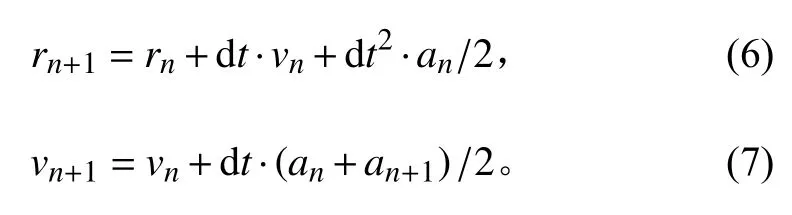
式中：r，v，a分別為粒子運動的位移、速度和加速度；dt為時間步長；n為迭代輪次。

1.6 初始化

粒子系統的初始化包括區域邊界初始化和區域內部初始化，主要任務是確定初始狀態下的粒子分布和電荷屬性。

粒子系統區域邊界的初始化，根據輸入的幾何形狀和網格大小σ 要求，將帶電粒子均勻分布在邊界上，并保證帶電粒子正負相間。區域邊界上的粒子可以設置成固定在位置上不可移動的，也可以設置為在不破壞粒子間距的情況下（通過Lennard-Jones 勢）能夠沿著輸入幾何移動，本文使用了前一種定義方式。

粒子系統區域內部的初始化有2 種方法：

1）根據輸入幾何求出最小的外接矩形，在外接矩形中以網格大小σ 為間隔均勻布置帶電粒子，然后將落在輸入幾何區域邊界外的帶電粒子以及距離區域邊界較近的粒子刪除；

2）與鋪砌法類似，沿著輸入幾何邊界作為初始鋪砌前沿，根據前沿節點類型，在區域內逐步添加新的帶電粒子，并且鋪砌前沿不斷更新且向區域內部推進，直到繼續添加節點會導致與任意前沿節點距離過近為止。

使用第1 種方法布置帶電粒子效率很高，但是對邊界不敏感，即在旋轉圖形后，區域內的帶電粒子相對位置發生改變。使用第2 種方法對邊界敏感，但是算法復雜，效率較低。本文結合2 種方法，在區域內邊界附近位置采用第2 種方法，而在區域內且離邊界較遠的位置采用第1 種方法，兼顧效率和邊界附近帶電粒子分布的邊界敏感性。

1.7 邊界協調

如上所述，若采用邊界前沿推進法布置區域內帶電粒子，通常邊界附近的帶電粒子分布最終能得到較好的四邊形網格。但是若完全使用幾何外接矩形法布置區域內的帶電粒子，可能最終邊界上的網格質量就會較差。由于邊界上的固定帶電粒子對帶相同電荷的帶電粒子有排斥，而對帶不同電荷的帶電粒子有吸引，邊界上的帶電粒子電荷庫倫勢對于區域內的節點也有一定的場對齊作用。

為表述庫倫勢的場對齊作用，設置一個矩形區域。區域內開設兩相同方孔，在邊界上和區域內部均勻間隔布置不同電荷屬性帶電粒子，且距離邊界上帶電粒子最近的區域內部帶電粒子的電荷符號相同，如圖6 所示。

圖6 開設兩方孔的矩形區域初始粒子分布Fig.6 Initial particle distribution of rectangular region with two square holes

依靠庫倫力調整帶電粒子位置的方法，可以通過增加邊界上固定位置帶電粒子的帶電量，增加其作用于附近（2.5σ）自由帶電粒子的庫倫力，從而加強吸引異號電荷，排斥同號電荷的能力，粒子運動模擬結果如圖7 所示。需要說明的是，如果邊界上帶電粒子的帶電量并不明顯大于區域內其他帶電粒子的帶電量，或者作用粒子與邊界上粒子的距離較遠，位置調整的作用則不是很明顯。

圖7 增加邊界上帶粒子電量后矩形區域最終粒子分布Fig.7 Final particle distribution of rectangular region after increasing the charge of the particle on the boundary

調整帶電粒子的帶電量，本質上是調整Lennard-Jones 勢和庫倫勢之間的比例關系。由上文所述，并不能通過無限增加庫倫勢的比重達到場對齊的目的，這可能導致帶電粒子之間的間距不穩定（異號粒子間距偏小，同號粒子間距偏大），所以本文僅在邊界上增加了帶電粒子的電量為區域內粒子電量的10 倍，并未增加區域內的自由粒子的電量。圖7 中粒子數量的減少是由于粒子運動時方向的不確定可能向同一個方向聚集，通過算法刪除局部多余粒子，增加空隙處粒子的原因造成的。而圖中仍缺少的粒子可由后文提及的異常處理方法處理。

2 網格劃分

在粒子運動模擬完成之后，即可根據區域內的粒子分布進行網格劃分。最簡單的方法是先將區域內網格進行三角網格劃分，然后合并相鄰三角形單元獲得四邊形單元。

2.1 Delaunay 三角網格劃分

Delaunay 三角剖分算法具備許多優異特性：1）最接近的三點形成三角形，且各三角形的邊皆不相交；2）不論從區域何處開始構建，最終都將得到一致的結果；3）任意2 個相鄰三角形形成的凸四邊形的對角線如果可以互換的話，那么2 個三角形6 個內角中最小的角度不會變大；4）如果將三角網中的每個三角形的最小角進行升序排列，則Delaunay 三角網的排列得到的數值最大；5）新增、刪除、移動某一個頂點時只會影響臨近的三角形，等等。

Delaunay 三角剖分算法默認劃分區域的邊界是一個凸多邊形的外殼，所以在處理非凸區域的時候需要進行一些額外的處理，將位于網格劃分區域外的網格予以刪除。

2.2 三角形網格合并

在初始化階段，正負粒子在網格劃分區域邊界上交替分布，除了上文所述的場對齊作用外，還為區域內的全四邊形網格提供了必要條件，即邊界上的節點個數為偶數。所以，為了盡可能使得三角形網格合并后依然能獲得四邊形網格，合并后的單元邊界也應該是正負電荷交替分布的。

為此，在Delaunay 三角剖分的基礎上，刪除所有連接同號粒子的邊，并由此形成一系列偶數邊形網格，如圖8～圖10 所示。在圖9 中，若四邊形有一條邊上2 個端點的粒子電荷符號相同，則一定還存在另一條邊，其端點的粒子電荷符號也是相同的，即至少還有一條邊會被取消，從而生成偶數變形網格。

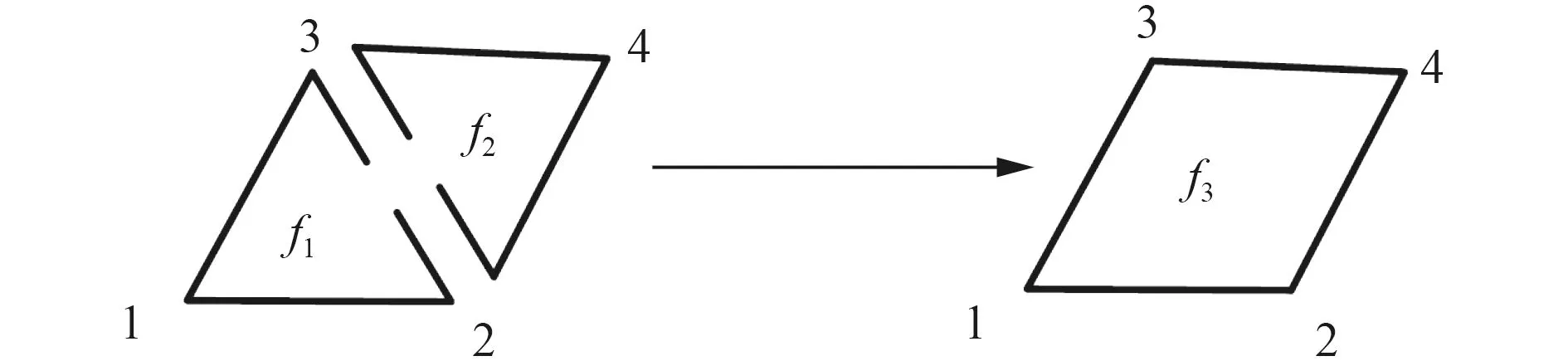
圖8 三角形網格與三角形網格合并Fig.8 Triangular mesh merges with triangular mesh

圖9 三角形網格與多邊形網格合并Fig.9 Triangular mesh merges with polygonal mesh

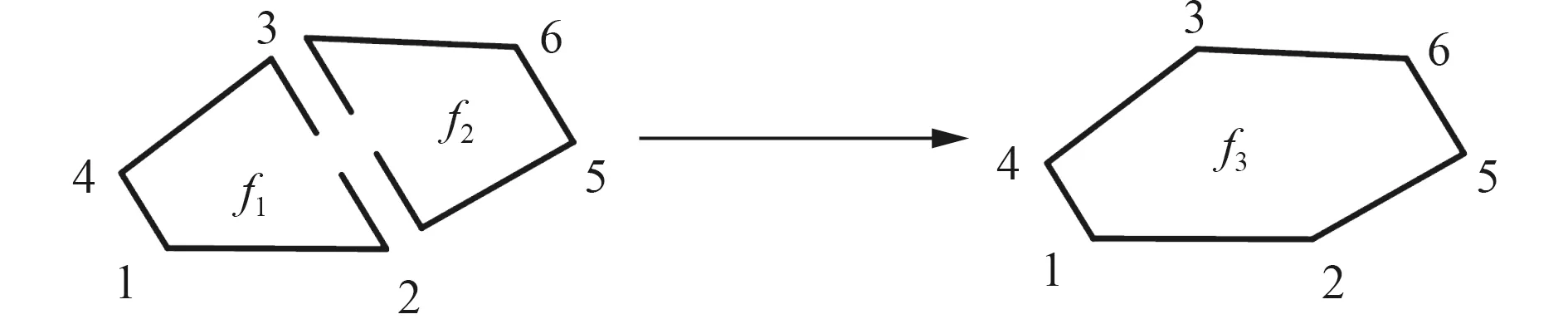
圖10 多邊形網格與多邊形網格合并Fig.10 Polygonal mesh merges with polygonal mesh

2.3 多邊形網格分解

如果三角形合并后得到的是四邊形網格，且該四邊形網格的4 個頂點電荷正負交替排列，則可以認為是一個最終的四邊形單元。

也有可能三角形網格合并后會得到六邊形、八邊形等一系列偶數邊形單元。為了將這些非四邊形的偶數邊形單元分解為四邊形單元，可以按如下步驟進行：

1）在多邊形中插入一個中心點，此處可取為多邊形的形心點，也可以是多邊形各頂點坐標的算數平均；

2）在多邊形邊界點上尋找與所插入點最接近的點，此時判定所插入點的電荷符號與該點的電荷符號異號；

3）在多邊形中從最近點開始，依次取出3 個頂點，與多邊形中心點一起組合成四邊形；

4）重復此過程，直到多邊形頂點全部使用完。

上述過程具體如圖11 所示。

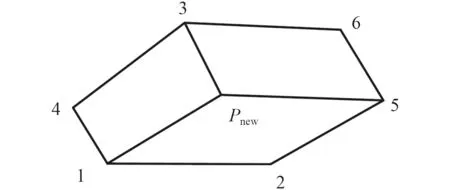
圖11 多邊形網格分解Fig.11 Polygonal mesh decomposition

2.4 異常處理

一類問題是網格尺寸較大，網格劃分區域中的節點數量極少，甚至只使用邊界上的節點參與網格劃分，此時實際上為粗網格劃分。使用上述流程可能無法獲得較好的結果，此時，在Delaunay 三角剖分后不考慮粒子電荷，僅使用最優三角形合并（即合并得到的四邊形質量和與其他三角形合并得到的四邊形質量相比是最高的）得到的結果可能更為理想，但是結果可能會出現三角形網格。

還有一類問題是網格尺寸較小，但是由于粒子的運動，在網格劃分區域中出現了一些交大的空隙，使用上述插入點獲得的四邊形網格尺寸遠大于要求網格尺寸。此時可以以該多邊形網格為新邊界，迭代本文所述網格劃分的整個過程。由于多邊形網格的邊界是由正負電荷粒子交替布置，與上文所述區域邊界初始化過程要求一致。

2.5 光順

由三角形合并得到的四邊形網格，以及通過多邊形網格降解生成的四邊形網格質量可能較差，可以按下式進行光順處理[7]：

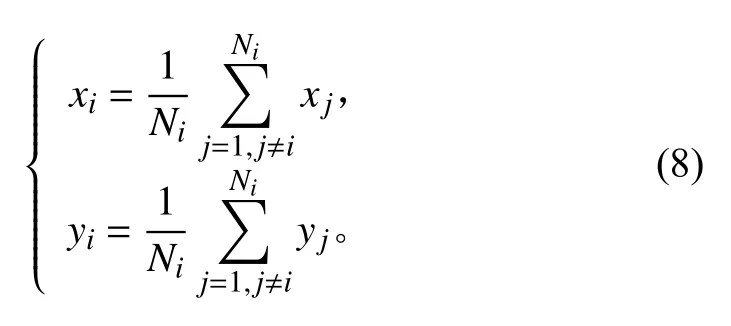
式中：Ni為與節點i所連接的節點總數；j為與i連接的節點；xi，yi分別為節點i的橫坐標與縱坐標。

3 實 例

3.1 開孔矩形板

開孔矩形板長2 000 mm，寬800 mm，正中心開一個腰圓孔，開孔大小為400×600。過程中使用的粒子，連接拆解的網格邊線，以及最終的網格單元如圖12 所示。為顯示網格劃分結果，僅顯示板格的左半邊，右半邊與左半邊對稱。

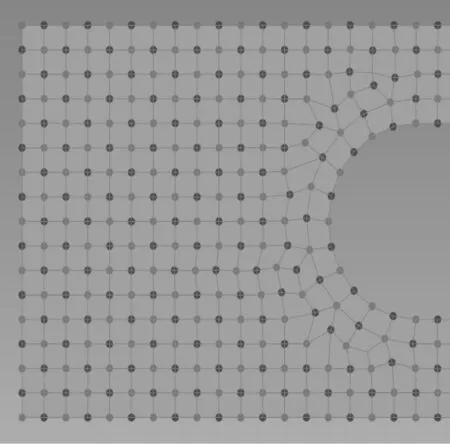
圖12 腰圓開孔板網格劃分實例Fig.12 Mesh of plate with opening

3.2 圓弧肘板

圓弧肘板臂長800 mm，圓弧大小1 000 mm。過程中使用的粒子，連接拆解的網格邊線，以及最終的網格單元如圖13 所示。在肘板趾端狹窄處出現了四邊形有三點共線的情況，導致出現了畸形四邊形單元。可以通過與圓弧邊上四邊形合成為偶數邊多邊形再拆解的方式解決，但是本例較注重圓弧邊緣的網格質量，所以僅將非圓弧邊緣的四邊形網格拆解成2 個三角形處理。

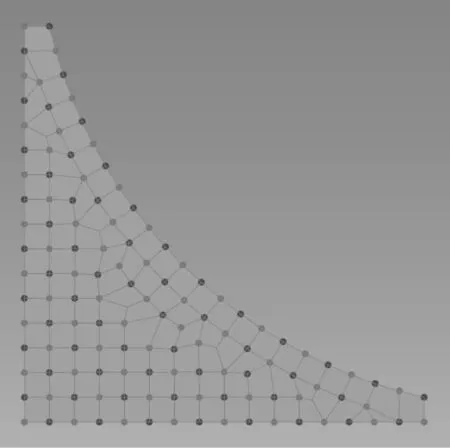
圖13 圓弧肘板網格劃分實例Fig.13 Mesh of arc bracket

3.3 縱骨穿越孔

圖14 為型號HP200×10的球扁鋼縱骨穿越孔，為清楚描述開孔形狀，網格大小設置為10 mm×10 mm。

圖14 縱骨穿越孔網格劃分實例Fig.14 Mesh of longitudinal cut-out

4 結語

為了靈活處理船體結構參數化建模，本文提出了一種基于分子動力學的網格劃分方法。該方法具有以下優點：1）避免了許多算法上的復雜性，易于編程實現；2）理論上能適應各種不同的邊界條件，較為靈活；3）最好情況下能實現全四邊形網格劃分。

但是在實踐過程中，該方法仍存在如下不足：1）由于是基于分子動力學，如果僅使用中央處理器單核運算計算速度較慢。但是該算法的每個粒子在某一時刻的運動是可以并行計算的，利用圖形處理器可大大節省時間；2）目前網格劃分密度是全局一致的，但是想要在粗網格中嵌入細網格，需要進一步考慮網格過渡問題。