一種求解交通網絡中最短路徑問題的人工蜂群算法

王 玉, 申鉉京, 周昱洲， 林鴻斌

(1. 吉林大學 計算機科學與技術學院, 長春 130012； 2. 吉林大學 軟件學院， 長春 130012)

隨著智能交通系統的應用越來越廣泛, 車輛路徑規劃作為智能交通系統的一項基本功能, 因而得到越來越多的關注. 目前, 對于靜態交通網絡的車輛路徑規劃研究已有很多結果： 張波良等[1]對靜態路網中的各算法進行了比較; TNR算法[2]用表查找完全替代了Dijkstra搜索, 使其加速比達100多萬; 文獻[3]進一步將TNR算法與邊標記法相結合, 加速比提升至300多萬. 但實際交通網絡總在不斷變化, 而忽視路網環境的變化很可能使車輛陷入交通擁擠的狀態中, 因此, 在靜態交通網絡中獲取的最短路徑通常不能很好地滿足人們出行的需求, 動態網絡下的路徑規劃更具有實際意義. 交通路網中各條道路的通行時間是不斷變化的, 即滿足網絡中弧的行走時間是時間的函數這一特性. 故交通網絡是一個時間依賴網絡(簡稱TDN網絡). 譚國真等[4]將TDN網絡分為先進先出(FIFO)型與非FIFO型, 并證明在FIFO型網絡中可采用Dijkstra算法求解, 而非FIFO網絡則不可行; 王海梅[5]通過對路網進行分析認為, 當路徑尋優的對象為機動車輛時, 道路交通網絡具有FIFO網絡的特性.

本文針對在TDN網絡中求解最短路徑問題, 提出一種基于人工蜂群算法的解決方案, 相比于遺傳算法[6], 該算法具有控制參數少、 易實現的特點. 同時, 根據FIFO網絡的特性對算法中的路徑選擇策略進行改進, 進一步提升算法的執行效率.

1 問題描述

定義1[7]圖G={V,E,F(t)}稱為時間依賴網絡TDN, 其中V={1,2,…,n}為頂點集合,E={(i,j)|i≠j,i,j∈V}為邊集合,F(t)={fi,j|(i,j)∈E}為邊權函數的集合,fi,j(t)為時間t的函數,t∈[a,b],b>a≥0.

定義1中的TDN網絡是連續的, 而在研究交通網絡時, 由于交通網絡在連續的一段時間內變化較小, 因此為簡化計算, 通常將交通網絡離散化處理. 離散時間情形下的TDN網絡模型為

G={V×T,E,F},

其中:T為感興趣的時間閉區間[t0,tm],T={t0,t0+Δ,t0+2Δ,…,t0+(M-1)Δ,…,tm},Δ表示一段較短的連續時間, 本文設Δ=5 min;V×T={(i,tj)|i∈V,tj∈T}表示節點的狀態空間, 有序對(i,tj)表示節點的一個狀態, 節點i在不同時間段內可能有不同的狀態.

2 人工蜂群算法

人工蜂群(artificial bee colony, ABC)算法[8]是一種基于群智能的全局優化算法, 其通過模仿蜂群尋找食物的過程解決問題. 該算法包括3類核心元素： 食物源、 雇傭蜂和非雇傭蜂; 以及兩種基本操作： 招募蜜蜂和放棄食物源. 其中: 食物源表示待解決問題的可能解； 雇傭蜂在食物源附近進行領域搜索, 并通過“8”字舞的方式分享食物源信息; 非雇傭蜂可分為觀察蜂和搜索蜂, 觀察蜂在獲取雇傭蜂的信息后根據食物源的質量選擇是否前往, 搜索蜂尋找新的有價值的食物源.

人工蜂群算法是為解決函數優化問題而提出的, 目前在多領域廣泛應用, 本文對該算法的編碼方式以及種群生成方式進行離散化處理, 以適應最短路徑問題.

2.1 編碼策略

因為車輛路徑規劃屬于離散問題, 所以本文采用自然數編碼的方式, 即采用自然數對路網中的每條邊進行編號, 而一條路徑是由這些編號組成的隊列, 隊列中的編號允許重復. 由于實際應用中因為交通規則的限制, 因此最優路徑中可能會出現環路.

2.2 路徑選擇策略

人工蜂群算法的收斂依賴于一個具有多樣性的種群, 本文用每條從起始節點至目的節點的可行路徑表示種群中的每個個體. 其中路徑的搜索過程為： 從起始節點開始, 按照路徑選擇策略選取一個鄰接節點作為下一個節點, 持續此操作, 直至目的節點. 因此, 路徑選擇策略直接影響路徑選擇的優劣, 進而影響種群的收斂速度與效果.

文獻[9]在蟻群選擇路徑時加入了方向引導, 該方法可有效縮小搜索空間. 在真實路網中由于地形和交通規則等限制, 并非所有的邊都可以到達終點, 所以在有些邊上可能會出現無下一條路可選的情形. 為防止下次路徑搜索時再進入該邊, 本文加入一個禁忌表用于記錄該類邊. 路徑搜索策略(為敘述方便， 記為路徑選擇策略1)如下：

為方便描述, 設當前路徑的終點為j.

步驟1) 搜索所有與當前路徑終點相連接的邊, 加入邊隊列;

步驟2) 從候選隊列選取一條邊ei, 并將其出隊;

步驟3) 判斷邊ei是否可以駛離當前路徑終點, 如果可以則轉步驟4); 否則轉步驟7);

步驟4) 檢查邊ei是否存在于禁忌表T中, 如果不存在則轉步驟5)； 否則轉步驟7)；

步驟5) 檢查邊ei是否違反轉彎限制, 如果不違反則轉步驟6)； 否則轉步驟7)；

步驟6) 做邊ei起點到終點的向量vi, 計算vi與vj的夾角, 將邊ei加入候選列表, 轉步驟7);

步驟7) 判斷邊隊列是否為空, 如果為空則轉步驟8)； 否則轉步驟2);

步驟8) 判斷候選列表是否為空, 如果為空則將邊ei加入禁忌表； 否則轉步驟9)；

步驟9) 計算候選列表中每條邊的選擇概率；

步驟10) 采用輪盤賭策略在候選列表中選擇一條邊加入路徑, 并計算加入后的路徑成本.

2.3 領域搜索策略

一條路徑的領域搜索策略為： 在路徑的第2個節點至第(n-1)個節點中隨機選擇一個節點, 并刪除此后全部節點; 從該節點開始, 按照路徑選擇策略重新搜索一條能到達目的節點的路徑.

2.4 人工蜂群算法執行步驟

1) 初始化參數, 產生初始食物源;

2) 進行迭代判斷, 若不滿足結束條件則轉步驟3)； 否則轉步驟7)；

3) 雇傭蜂到蜜源附近進行領域搜索發現新的食物源, 若新食物源優于原食物源, 則用新食物源替代原食物源, 否則保持原食物源;

4) 跟隨蜂根據雇傭蜂分享的信息按食物源的質量進行概率選擇食物源, 并在食物源附近進行領域搜索;

5) 判斷雇傭蜂領域搜索次數, 當達到控制參數閾值時, 如仍未找到更優的食物源, 則放棄其對應的食物源, 將雇傭蜂轉化為偵查蜂尋找下一個新的食物源；

6) 記錄當前最優解；

7) 輸出最優解.

3 改進人工蜂群算法

3.1 算法可行性

人工蜂群算法可適用于FIFO網絡和非FIFO網絡, 圖1為采用路徑選擇策略1生成的一條路徑. 由圖1可見, 當取路段長度作為路網中邊的權值時(即在靜態路網中), 在該靜態路網中存在若干條更短的路徑(圖1中紅色路段), 在替換原路徑中部分子路徑后一定可以使原路徑的距離更短.

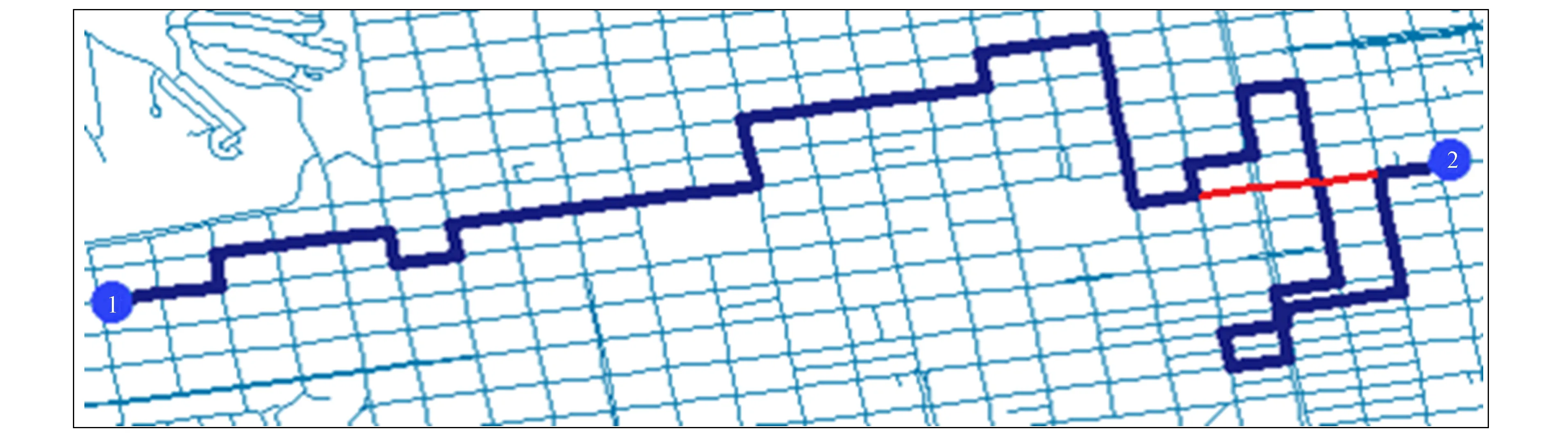
圖1 采用路徑選擇策略1生成的一條路徑Fig.1 Path generated by path selection strategy 1

定理1[10]如果網絡中每個圈的長度為非負, 則網絡中每條路徑的長度不小于相應的最短路徑長度, 且每條最短路徑的子路徑也是最短路徑.

定理2[10]在時變FIFO網絡中, 如果tS時刻從節點nS出發到達節點nD的最短時間路徑為

SP(nS,nD,tS)={(nS,tS),(n1,t1),…,(ni,ti),(ni+1,ti+1),…,(nj,tj),(nD,tD)},

則最短路徑SP(nS,nD,tS)的子路徑{(nS,tS),(n1,t1),…,(ni,ti)}和{(ni,ti),(ni+1,ti+1),…,(nj,tj),(nD,tD)}也一定是最短時間路徑, 其中ni是最短時間路徑上的任一中間節點.

對于TDN網絡, 若使用更短路徑替代原路徑中部分子路徑的方法也成立, 則蜂群算法中食物源的整體質量將會提升, 進而可通過減少食物源的數量以及算法迭代次數提升人工蜂群算法的運行速度. 由定理1和定理2可知, 該方法對于FIFO網絡成立, 即在FIFO網絡中, 當原路徑中某一段被另一段通行時間更短的子路徑替代時, 原路徑的通行時間也會縮短.

3.2 改進路徑選擇策略

在路網中能替代原路徑的時間更短子路徑可以有多種, 但實際上在搜索一條到達目的節點的路徑過程中, 每向路徑中加入一條路段之前都會遍歷到與該路段相鄰的路段, 而這些相鄰路段中可能存在更短子路徑[11-13]. 圖2～圖4分別為在路徑搜索時可能遇到的3種情形. 由圖2可見, 當邊ab加入路徑時記錄節點b, 當路徑加入邊bf時檢查節點b是否有過記錄, 若存在路徑abf能通行, 則用其代替原子路徑abcdebf.

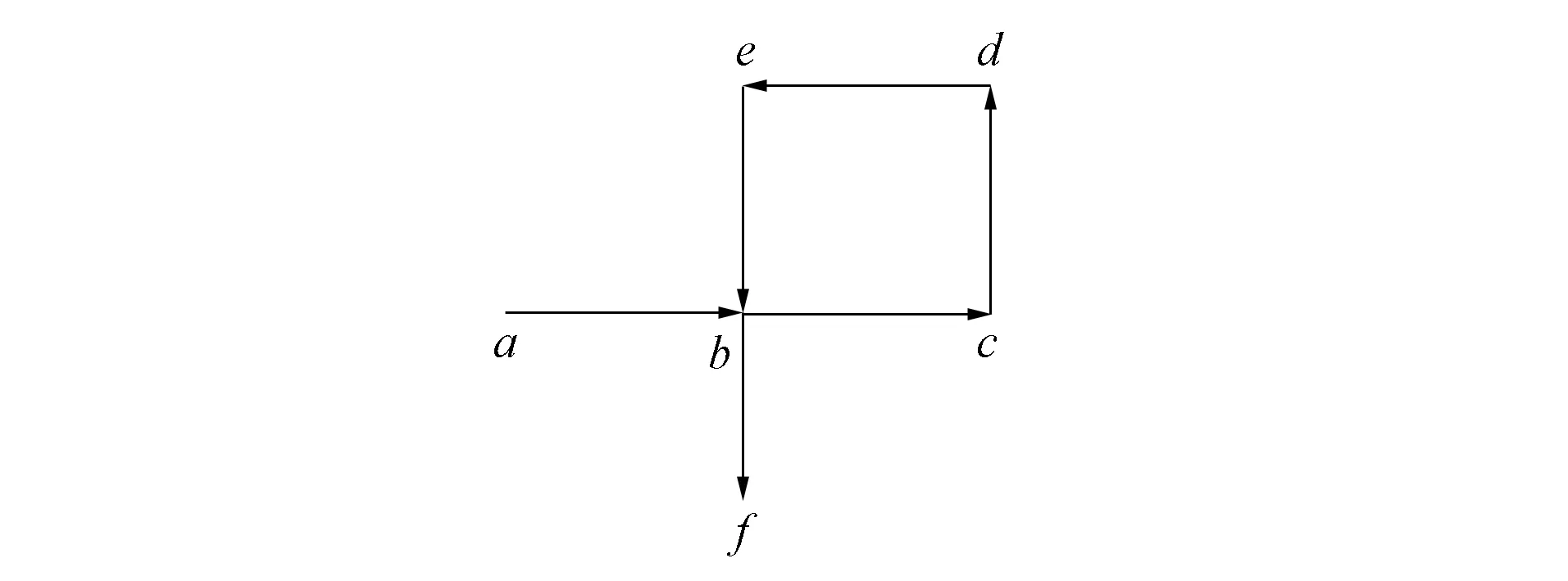
圖2 路徑中存在環Fig.2 Rings in path

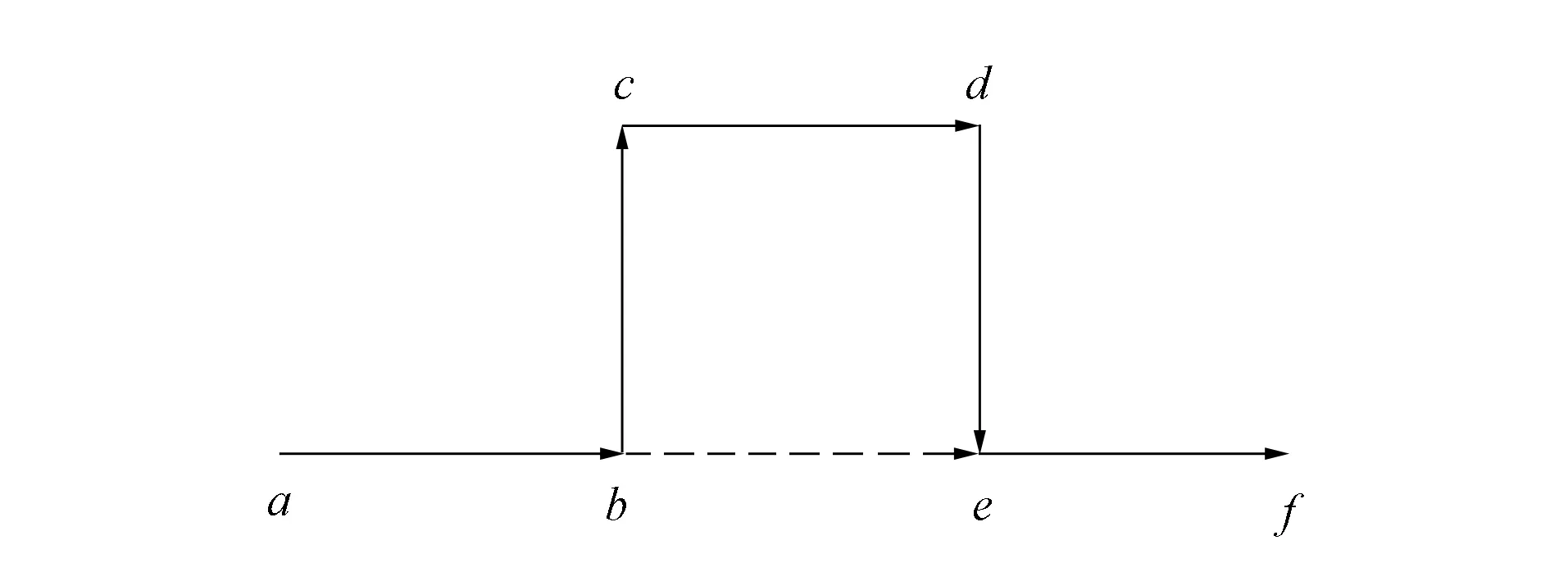
圖3 原路徑中某子路徑可用一條邊替換Fig.3 Subpath in original path can be replaced by an edge

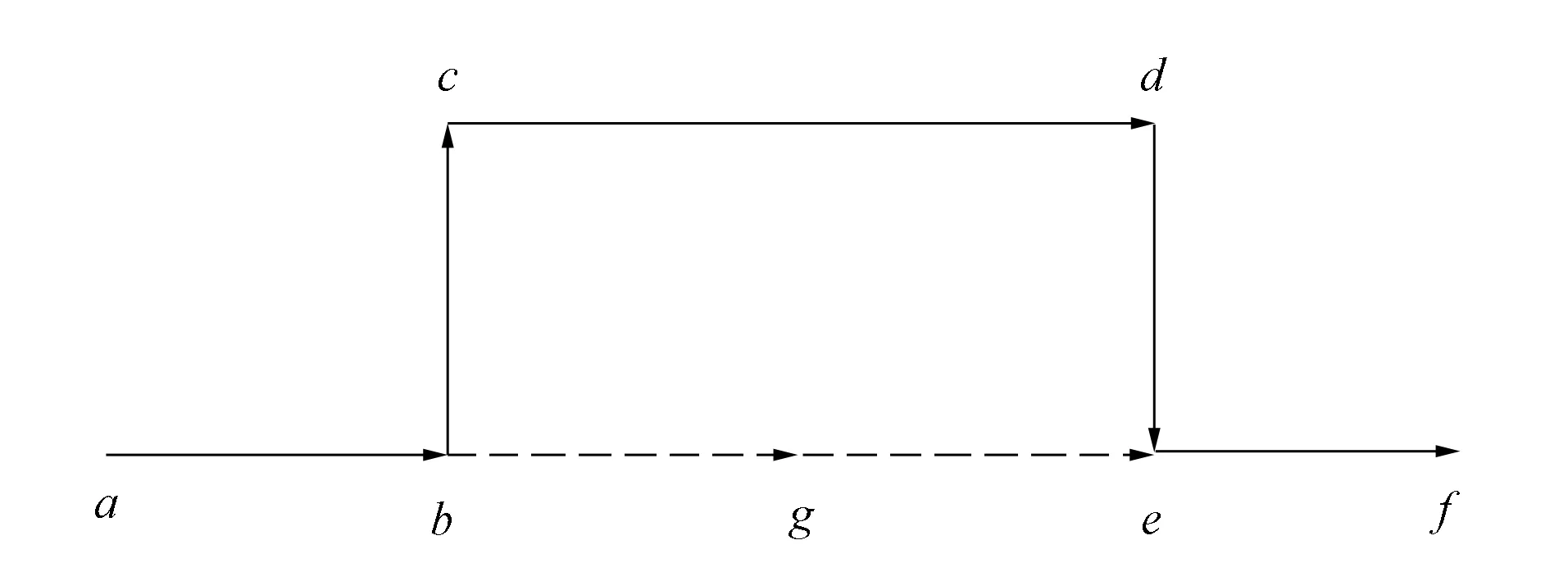
圖4 原路徑中的子路徑可用兩條相鄰的邊替換FIg.4 Subpath in original path can be replaced by two adjacent edges

由圖3可見, 當邊bc加入路徑時記錄候選邊be和節點e, 當路徑加入邊ef時檢查節點e是否有過記錄, 若有根據節點e找到邊be, 檢查路徑abef能否通行, 如果可以, 則可用其替換路徑abcdef.由圖4可見, 當邊bc加入路徑時, 記錄候選邊bg和節點g, 當路徑加入邊ef時, 遍歷駛向節點e的邊, 若遍歷到邊ge是, 則檢查節點g是否有過記錄, 若有根據節點g找到邊bg, 則檢查路徑abgef能否通行, 如果可以, 則可用其替換路徑abcdef.

針對上述3種情形, 對路線選擇策略1進行如下改進.從候選列表中選一條將要加入路徑的邊e, 對當前路徑中最后一條邊的候選節點j及其候選駛入邊做以下判斷：

判斷1) 候選節點j在路徑中是否出現兩次以上, 如果是, 則表明該路徑存在重復部分, 判斷重復部分是否可以刪除, 若可以, 則記錄刪除后的路徑通行成本, 并加入候選優化方案中.

判斷2) 候選節點j是否在候選邊中出現過, 若出現過, 則表明可能存在一條更短子路徑, 判斷選擇該子路徑是否違反轉彎限制, 如果不違反, 則計算從該子路徑通行的成本, 并與原路徑通行成本進行比較, 如果優于原路徑, 則將其加入候選優化方案中.

判斷3) 依次遍歷j的候選駛入邊, 判斷候選駛入邊的起始節點是否在候選節點中出現, 若出現, 則表明可能存在一條更短子路路徑, 進行與判斷2)相同的操作.

當以上判斷完成后, 從候選優化方案中選擇通行成本最優的方案對路徑進行修改, 最后將之前選擇的邊e加入路徑.

3.3 附加數據結構

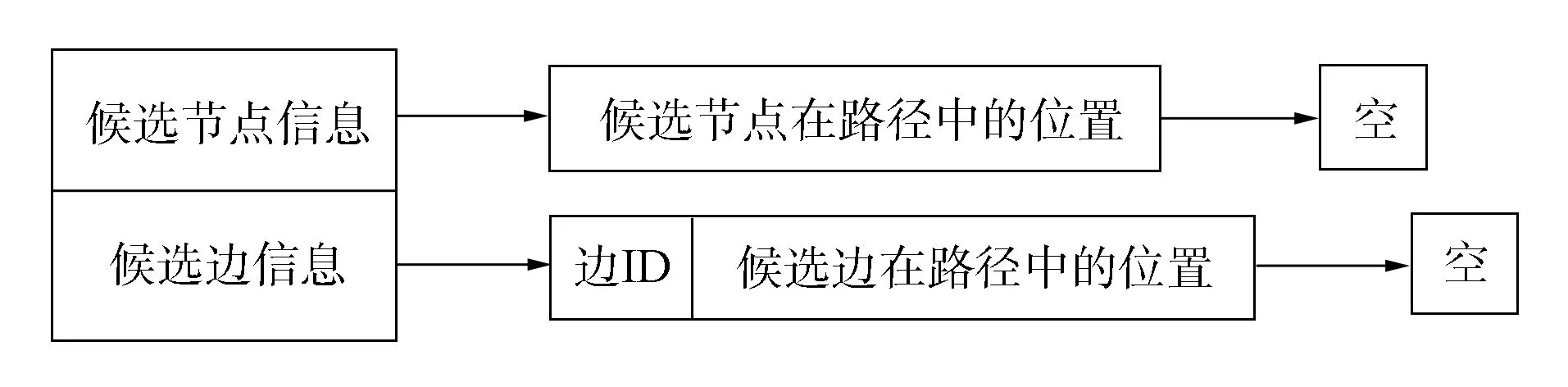
圖5 候選節點記錄表結構Fig.5 Structure of candidate node record table

為完成上述功能, 本文在原路徑基礎上添加一張候選節點記錄表, 該表采用散列存儲結構, 以應對大量的查找需求.為描述方便, 本文將一條邊的終點稱為候選節點, 例如圖2中邊ab的候選節點為b, 圖3中邊be的候選節點為e.而將以某個候選節點為起點, 但未加入路徑中的邊稱為候選邊, 例如圖3中的邊be和圖4中的邊bg.將駛入某個候選節點但又不屬于路徑上的邊稱為候選駛入邊.候選節點記錄表結構由記錄索引和候選節點記錄組成, 其中記錄表索引為候選節點在路網中的編號.候選節點記錄表結構如圖5所示.候選節點信息用于記錄候選節點是否位于路徑上, 由于節點在路徑中可能出現多次, 故采用鏈表結構進行記錄.候選邊信息用于記錄候選節點所在的候選邊, 同樣由于候選邊的個數不唯一, 所以該信息也采用鏈表記錄.

圖6為某條搜索到的路徑, 其中實線表示路徑, 虛線表示候選邊.圖6中候選節點e和g在候選節點記錄表中的記錄分別如圖7和圖8所示.

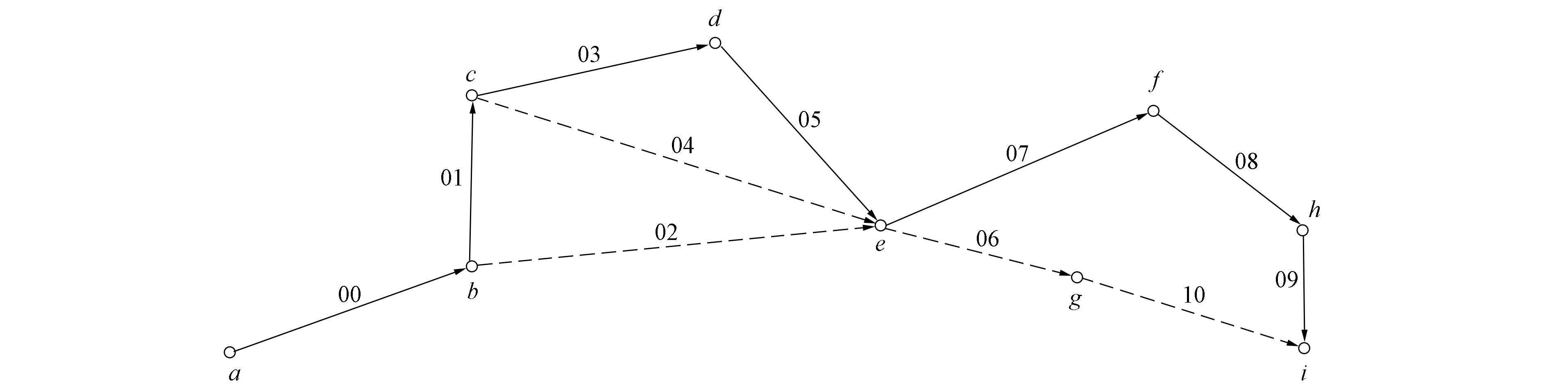
圖6 某條搜索到的路徑Fig.6 A found path

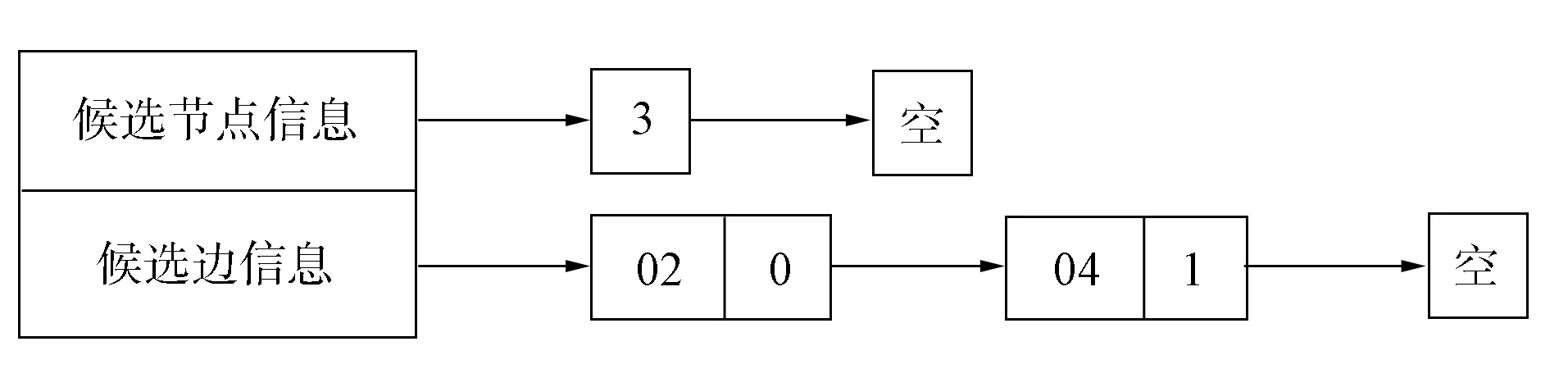
圖7 節點e在候選節點記錄表中的記錄Fig.7 Record of node e in candidate node record table

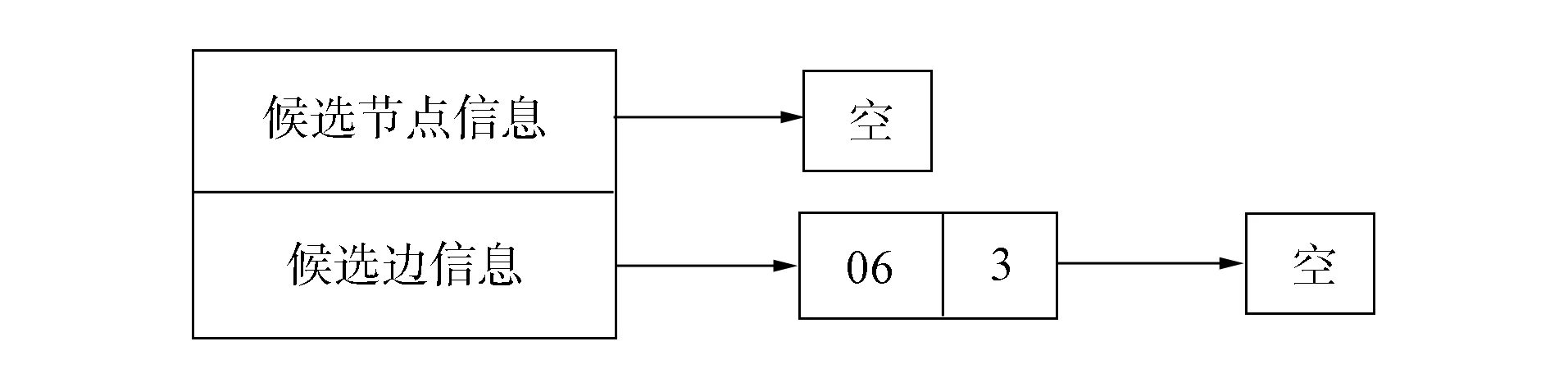
圖8 節點g在候選節點記錄表中的記錄Fig.8 Record of node g in candidate node record table

為方便在刪除路徑時對記錄索引表進行維護, 對路徑中的每條邊附加一個候選邊記錄表, 用于存儲候選邊和候選節點, 如圖9所示.圖6中邊05在候選邊記錄表中的記錄如圖10所示.

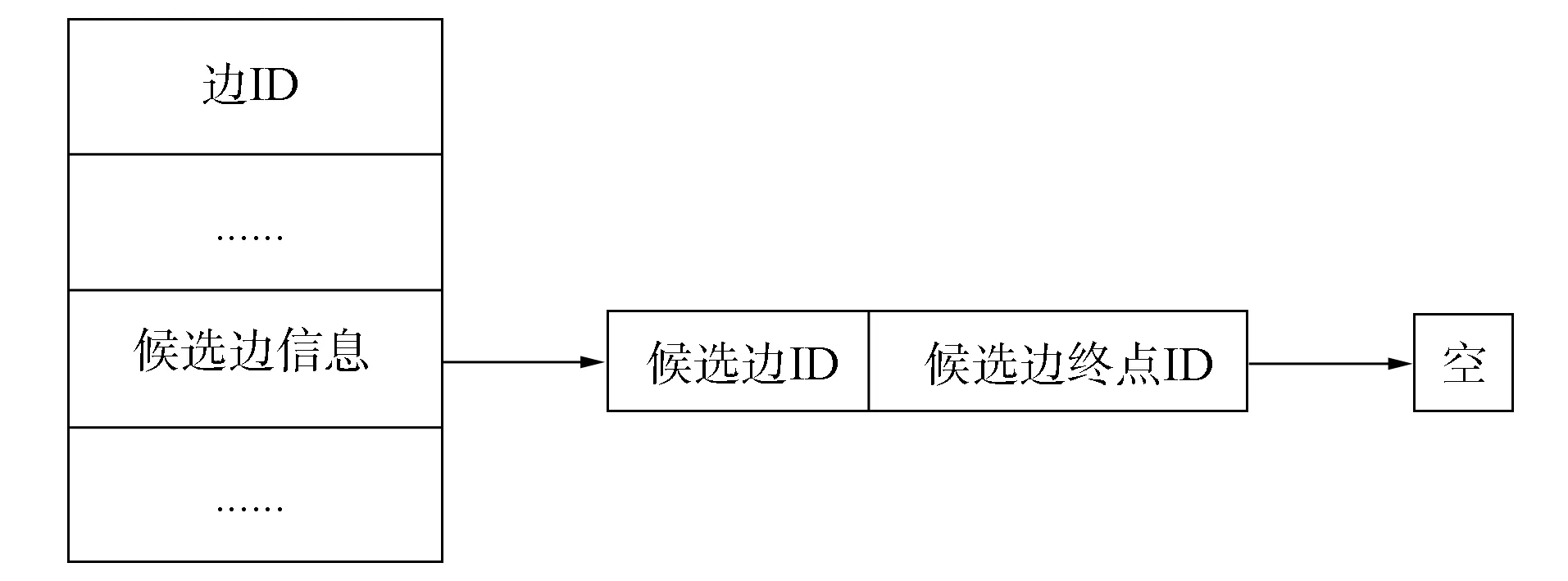
圖9 候選邊記錄表結構Fig.9 Structure of candidate edge record table

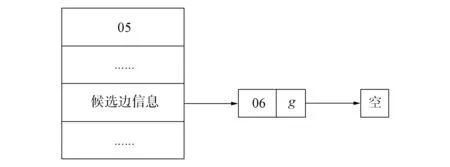
圖10 圖6中邊05在候選邊記錄表中的記錄Fig.10 Record of edge 05 of Fig.6 in candidate edge record table

在增加該數據結構的基礎上對原路徑選擇策略進行如下修改：

步驟1) 初始化最優路徑成本為原路徑的通行成本;

步驟2) 篩選路徑末端的可通行路徑, 將滿足通行條件的路徑加入當前最后一條邊的候選邊記錄表中;

步驟3) 選擇一條將要加入路徑的邊, 并將其從候選邊記錄表中移除;

步驟4) 篩選路徑末端節點的駛入邊; 并將駛入邊的起始節點ID作為記錄索引在候選節點記錄表中搜索, 若搜索到記錄則表明路徑可能存在一條更優子路徑;

步驟5) 計算該更優路徑的通行成本, 若優于最優路徑成本, 則將其替換為該更優路徑成本, 同時記錄該更短路徑;

步驟6) 根據記錄的更短路徑修改原路徑, 同時修改候選節點記錄表.

4 實驗對比分析

為驗證路徑選擇策略改進方案的有效性, 利用ArcEngine 10.0在JAVA編程環境中進行仿真實現. 實驗數據采用ArcGIS提供的美國舊金山交通網絡, 該交通網絡共有108 226條邊, 37 695個節點, 并使用歷史流量信息構建了基于行駛時間的成本模型. 實驗隨機選取一對起始點和終點, 設種群規模為30, 閾值為10, 迭代次數為60, 分別采用兩種路徑選擇策略各計算30次, 兩種路徑選擇策略下算法的收斂性對比如圖11所示. 表1列出了一對起始點終止點查找60次的路徑平均實驗結果.

表1 一對起始點終止點查找60次路徑的平均實驗結果

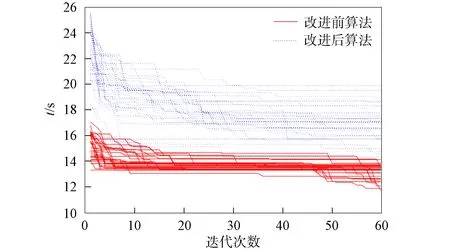
圖11 算法改進前后的收斂性對比Fig.11 Convergence comparison of algorithms before and after improvement

由圖11和表1可見, 改進后算法的路徑選擇策略在同等條件下初始化值和最終收斂值均優于改進前算法, 在計算時間上前者略高于后者. 為證明該改進方法具有普遍的適應性, 本文又隨機選取了5對起始點和終點進行實驗, 結果列于表2.

由表2可見： 1) 在多組實驗中, 改進后的路徑選擇策略表現均優于改進前的策略, 表明該項改進具有普適性； 2) 改進后的路徑選擇策略使算法在每次迭代的時間花費上比改進前約多50%, 但結果卻遠優于改進前的策略, 甚至前者初始解的質量已優于后者迭代數十次后得到的解, 因此該項改進可極大減少算法的迭代次數, 從而減少算法的總計算時間.

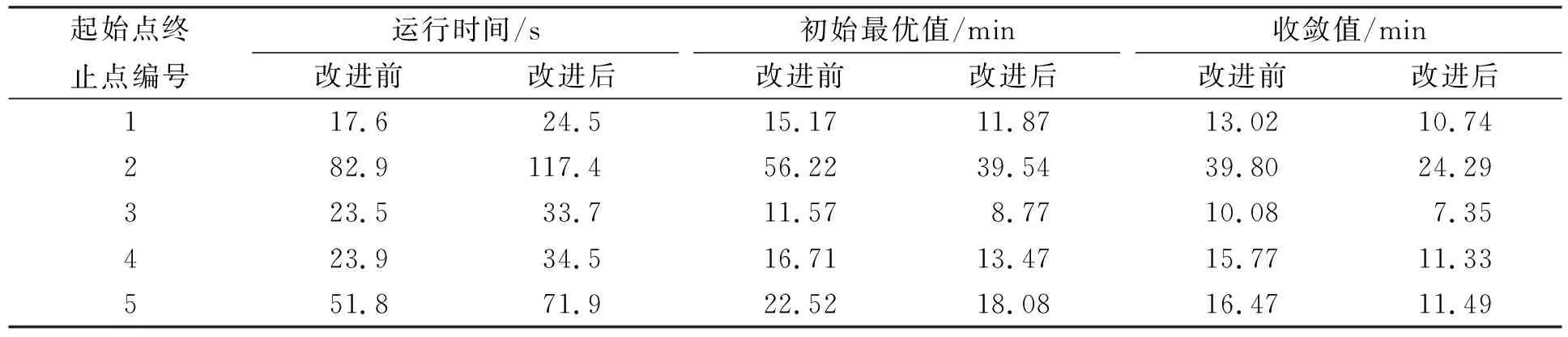
表2 5對起始點終止點分別查找一次路徑的實驗結果

綜上所述, 動態路網是典型的時間依賴網絡, 該網絡中的最短路徑規劃問題具有應用價值. 本文利用人工蜂群算法解決時間依賴網絡中的最短路徑問題, 針對動態路網以出行者為尋優對象時, 可將路網視為FIFO網絡這一特性, 對原算法中的個體生成環節進行了改進, 并采用JAVA語言在ArcGIS平臺提供的動態路網上進行了仿真實驗, 實驗結果表明, 該改進策略合理、 有效.