基于多元表征完善CPFS結構

陸建

摘? 要：在數學概念教學中，實施多元表征教學，有利于學生完善CPFS結構，優化概念認知，促進概念的理解融通. 橢圓概念的表征形式有模型表征、操作表征、方程表征、軌跡表征等. 運用多元表征教學時要注意兩點：增加結點，豐富連線;合理取舍，把握時機.

關鍵詞：多元表征;CPFS結構;橢圓

南京師范大學喻平教授提出了CPFS結構理論，其中個體CPFS結構是指學生頭腦中的知識網絡，是學生在數學學習中特有的認知結構. 它由下列四個概念組成：概念域（Concept field），指學生在學習一個概念時頭腦中形成了一組等價定義;概念系（Concept system），指學生在學習新概念時頭腦中形成了一組相關概念及相互之間的關系;命題域（Proposition field），指學生在學習命題后頭腦中形成了一組命題;命題系（Proposition system），指學生頭腦中貯存了一組命題，以及相互存在的推理關系.“CPFS”即概念、命題、域、系四個單詞的首字母縮寫. 相關研究指出，CPFS結構對學生的數學理解、學習、遷移、探究問題、解決問題等能力都會產生直接的正面影響. 因此，CPFS結構理論對數學教學具有很好的指導意義，它要求教師努力完善學生的知識網絡，幫助他們形成完備的認知結構.

多元表征是指對一個信息加工對象，通過心原碼的建構過程，對信息進行編碼并形成多種轉譯，從而形成對信息的多元化表征形式. 學生能用不同的形式表征數學概念，實現多元表征的融合轉化，形成相對完善、精致的概念網絡是對數學概念理解融通的標志. 有研究表明，個體形成的CPFS結構與問題表征有密切聯系，具備優良CPFS結構的學生更能合理、正確地表征問題，進而有效地解決問題. 可見，在數學概念教學中，完善學生CPFS結構，有利于實施多元表征教學，優化概念認知，促進概念的理解融通. 下面以“橢圓”概念教學為例，談談這方面的思考，敬請批評指正.

一、“橢圓”概念的多元表征

1. 模型表征：追尋原始形態，感受幾何魅力

數學概念是從大量數學現象甚至現實事物中比較、概括、抽象得到的，大多數概念都有一段厚重的歷史，往往是經過數學家艱辛探索、反復求證、逐步完善得到的. 而在現實教學中，教師常常忽略概念的形成過程，直接教授學生現成的結論，學生無法體會到概念背后發現的曲折、探索的艱辛、思維的跌宕. 正如荷蘭數學教育家弗賴登塔爾所說，沒有一種數學思想是以它們被發現時的樣子公開發表出來，一個問題被解決后，相應地發展為一種形式化技巧，結果把求解丟一邊，使得火熱的發現變成了冰冷的美麗. 數學概念教學應追尋概念產生背后的思考，挖掘數學家當年的思維軌跡，讓學生感受數學家當初的困惑，重走數學概念發現之路，激起學生的認知沖突和探索興趣，使數學概念的產生自然而然、水到渠成. 筆者從以下幾個問題切入，引導學生理解橢圓的概念.

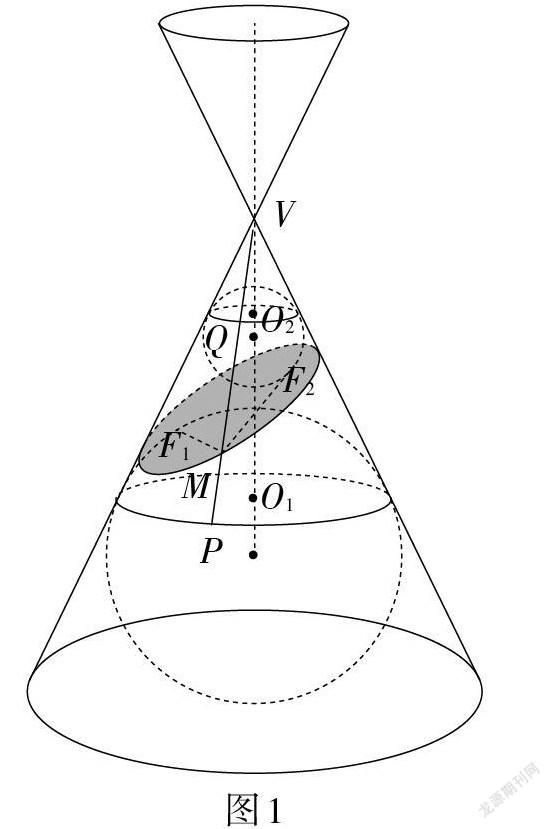
問題1：用一個既不與圓錐的軸平行、垂直，又不與母線平行的平面截圓錐面，所得到的截線具有什么幾何特征呢？

若用一個垂直于圓錐的軸的平面去截圓錐面，所得截線是一個圓，此時若在截面的上方、下方各放一個球，兩球與圓錐面及截面均相切，則兩個球與截面的切點均與截面圓心重合，截線上任一點到切點的距離為定值（截面圓的半徑）. 由此聯想到問題1，如圖1所示，若改變截面的位置，使截面既不與圓錐的軸平行、垂直，又不與母線平行，那么截線上的點滿足什么幾何性質呢？設點[M]為截線上任一點，由于此時切點由1個變為2個（點[F1]和點[F2]），類比前面的思考，自然想到需探究[MF1]與[MF2]的關系，抑或它們具有什么不變的性質.

1822年，比利時數學家旦德林構建了雙球模型，該方法利用純幾何知識，構建了橢圓的概念，構思精巧、論證嚴謹，滲透了數學之美，充分彰顯了幾何知識的魅力. 教師充分利用模型表征，追尋數學家探究的歷史軌跡，描繪橢圓概念發現的原始形態，在數學家的“廢紙簍”里找回火熱的思考，發展了學生的直觀想象和數學抽象素養，滲透了數學文化教育.

2. 操作表征：積累活動經驗，彰顯概念內涵

建構主義認為，數學學習并非一個被動的接受過程，而是一個建立在學生已有知識結構和經驗基礎上的主動建構過程. 按照這種觀點，最好的學習方法就是“做數學”. 正如弗賴登塔爾所說，數學是人的一種活動，如同游泳一樣，要在游泳中學會游泳. 我們必須在“做數學”中學習數學. 沒有經過比較分析、抽象概括、演繹歸納等深刻思維活動得到的概念是空洞的、標簽式的，是沒有靈魂的符號. 因此，在概念教學中，教師要以活動為載體，讓學生在“做數學”中，經歷深度的思維，學會數學地思考，積累數學活動經驗，從而把握數學概念的內涵.

問題2：給你一根定長的細繩，兩枚圖釘，一支鉛筆，能畫出橢圓嗎？

將細繩的兩端分別利用圖釘固定在點[F1，F2]，用鉛筆尖將繩子拉緊，使筆尖在畫板上慢慢移動，觀察筆尖的移動（即動點的變化），其數學特征是筆尖的每一個位置到兩個定點的距離之和不變，都等于細繩的長度，顯然畫出的圖形是一個橢圓.

問題3：準備一張圓形紙片，在圓內任取不同于圓心O的點[F]，將紙片折起，使圓周過點[F]，如圖2所示. 然后將紙片展開，就得到一條折痕[l]. 這樣繼續折下去，得到若干折痕，觀察這些折痕圍成的圖形的輪廓，它們形成了什么曲線？

學生形成了橢圓的概念后，并不代表學生真正理解了概念，還需要從不同的角度進行抽象概括，以固化概念本質屬性，深化學生對概念的理解. 教師通過“畫”“折”這兩個活動，形成操作表征，讓學生在“做數學”中感悟橢圓的定義，雖然我們在操作過程中花了很多時間，但學生積累了更多活動經驗，豐富了認知結構，概念域也逐步趨于完善，發展了直觀想象、邏輯推理素養.

3. 方程表征：構建數量關系，揭示本質特征

解析幾何的本質是用代數方法研究幾何問題，坐標系的建立，使得點可以用坐標表示，曲線可以用方程刻畫，進而使得通過代數方法研究曲線成為可能. 建立橢圓的概念后，僅從形的方面我們尚不能全面地認識、理解它，還需要從數的方面探索橢圓的代數表示，使得數與形完美結合，從而使形的研究能夠插上數的翅膀. 正如法國數學家拉格朗日所指出的，代數同幾何分道揚鑣，它們的進展就緩慢，它們的應用就狹窄，但是當兩門科學結成伴侶時，它們就能相互吸收新鮮的活力，從那以后，就以快速的步伐走向完善.于是接下來要探究的自然是：圍繞橢圓的幾何條件，挖掘橢圓上動點坐標滿足的數量規律，建立橢圓的方程，進而發揮代數的力量，借助方程研究橢圓的幾何性質.

問題4： 如何建立橢圓的方程？（推導過程略.）

這里，我們用數量關系與符號語言準確、簡潔地表征了橢圓的概念和橢圓的標準方程，建立了橢圓的幾何特征與數量關系之間的有機聯系. 橢圓的概念從幾何特征上反映了橢圓的本質屬性，而橢圓的標準方程則從數量關系上抽象出橢圓的本質規律. 運用橢圓的標準方程可以幫助學生從不同視角理解橢圓的概念，完善其概念域，解釋和驗證不同情境中橢圓不同呈現形式的同一性.

問題5與問題6都是從橢圓的方程表征入手，進行等價變形，從距離與斜率出發，由數到形認識橢圓的幾何特征. 通過橢圓的方程表征建立統一結構，打通多種幾何刻畫之間的相互聯系，把橢圓的相關性質予以統一，既抽象了橢圓的本質屬性，又豐富了橢圓的CPFS結構.

4. 軌跡表征：注重知識關聯，完善概念體系

世界是聯系的，聯系是有規律的，站在聯系的角度認識事物，有利于把握事物的本質與規律. 由于數學知識聯系緊密、邏輯嚴謹、結構緊湊，因此數學學習要突出知識之間的相互關聯，在聯系中理解知識的整體性和邏輯性，從而認識數學對象的本質，形成良好的認知結構. 學習、理解橢圓的概念，要基于聯系的視角，立足圓錐曲線整章學習，做到“瞻前顧后”，絕不能單打獨斗、孤立片面. 接下來，要進一步探索橢圓的多種表征方式，以豐富概念域，完善概念系.

此處，我們仍然是從運動變化的角度探究橢圓與雙曲線的聯系，展現了數學的統一美與和諧美. 其實，橢圓可以由雙曲線生成，雙曲線也可以由橢圓類似地生成，它們是互為“伴隨曲線”的. 全新的視角、多元的表征，帶給學生一個“不一樣”的、超凡脫俗的橢圓，至此對橢圓的理解透徹深刻，完善的CPFS結構悄然生成.

二、兩點思考

1. 增加結點，豐富連線

CPFS結構理論啟示我們，數學概念教學的重要目標是形成和完善學生的概念域、概念系及相關的知識網絡. 在CPFS結構中，數學概念等知識點處于結點的位置，而結點之間的連線常包含著重要的數學思想方法，由此形成的知識網絡結構是知識與方法的復合體. 結點和連線越多，任意兩個結點之間的通路也就越多，網絡也就越有效、越強大. 因此，形成和完善概念域和概念系的基本途徑是增加概念結點的數量，豐富概念之間的方法連線.

橢圓概念的多元表征，提供了認識橢圓的不同視角，使得圍繞橢圓的知識結點充足有效，而多種表征形式之間的相互溝通、融合、轉化，使結點之間的聯系更加緊密. 在表征轉換過程中，運用了定義法、直接法、轉移法、參數法、交軌法等求動點軌跡的基本方法，滲透了運動變化、選參消參、對立統一等數學思想，極大地豐富了知識結點之間的連線，有利于形成多元聯系、結構緊密的CPFS結構，有利于發展學生的直觀想象、邏輯推理、數學抽象、數學運算等素養.

2. 合理取舍，把握時機

盡管橢圓的概念有多種表征，但并非越多越好，由于學生在一節課中所能接受的內容是有限的，故不可能把所有的表征形式全教給學生，事實上，過多的表征信息可能會造成學生理解上的困難和混亂，反而得不償失. 因此，教師要根據教情和學情，合理選擇表征形式，同時要把握好各種表征形式出現的時機. 模型表征是滲透數學文化、優化直觀想象素養的好素材，但圖形復雜且過于抽象，因此教學中要做好鋪墊，使探究自然、過渡順暢、避免突兀. 同時，要發揮多媒體的作用，盡量減輕學生認知上的負擔. 對于操作表征，“畫橢圓”可以借助幾何畫板軟件來完成，“折紙片”可以讓學生課后實踐操作，體驗感悟. 三種形式的方程表征是教學的重點，要認真探究，要突出代數式的變形，培養學生的數學運算能力，引導學生挖掘代數式的幾何背景，深刻體會方程是曲線的“代數表示”. 對于軌跡表征，要結合具體的例題、習題，循環往復、螺旋上升，在不同的學習階段分散講解，讓學生在問題解決中體會橢圓的本質屬性. 在高三復習階段，可以圍繞橢圓概念的表征，專門設計微專題復習，力求見微知著，幫助學生系統地總結歸納，使學生對橢圓的認知由分散、不完整的印象上升到集中、完整的理解，形成更加牢固的、關于概念對象和結構的陳述性知識，再通過橢圓概念在解決相關問題中的反復應用，鞏固程序性知識，最后逐步完善概念域和概念系，形成結構優良，易于提取、遷移的CPFS結構.

參考文獻：

[1]喻平. 數學學習心理的CPFS結構理論[M]. 南寧：廣西教育出版社，2008.

[2]呂程，周瑩，唐劍嵐. 多元表征：探尋數學智慧課堂的一把密鑰[J]. 教育與教學研究，2012，26（6）：107-110，114.

[3]喻平. 個體CPFS結構與數學問題表征的相關性研究[J]. 數學教育學報，2003，12（3）：10-12，16.