基于強度應力比的擠壓性圍巖隧道承載拱變化規律研究

閆 迪， 劉志春， 李新志， 郭小龍

(石家莊鐵道大學土木工程學院，河北 石家莊 050043)

擠壓性圍巖是在高地應力環境下，隧道周邊一定范圍內產生顯著塑性變形或流變的巖體，具有高地應力、低強度、強流變的顯著特征[1-3]。擠壓性圍巖隧道具有變形量大、變形速率高、持續時間長的特點，如施工處理不當易產生變形侵限、支護開裂、隧道塌方等嚴重病害[4-5]。深埋隧道開挖后，周圍巖體產生應力重分布，通過圍巖內部應力調整及圍巖與支護相互作用，而形成能夠承擔一部分荷載的圍巖，稱為圍巖承載拱。在深埋隧道特別是超深埋的擠壓性圍巖隧道中，支護結構承擔的圍巖壓力遠小于圍巖初始地應力，這種現象可以用圍巖承載拱解釋。

目前，形成了較為統一的基于圍巖承載拱理論的圍巖穩定評價方法[6-8]，認為承載拱距離隧道開挖輪廓面越遠，圍巖越不穩定；圍巖承載拱厚度越大，則證明需要調動更多的圍巖承擔荷載，圍巖越不穩定。

針對深埋隧道應力狀態、承載拱范圍、承載結構等，以往學者采用理論解析、數值模擬、現場實測等方法已開展了大量研究工作，取得了諸多寶貴的研究成果[8-14]。目前對于一般圍巖的深埋隧道設計施工均從圍巖分級出發，近年來擠壓性圍巖隧道設計施工已轉變為從變形分級出發，根據不同變形等級進行隧道結構設計和施工控制[1-5]。本文基于變形分級，推導擠壓性圍巖隧道圍巖承載拱理論解，分析承載拱范圍變形等級(強度應力比)、洞徑、圍巖強度、隧道埋深、支護抗力的變化規律，從而解釋擠壓性圍巖隧道圍巖承載機理，為擠壓性圍巖隧道設計施工提供技術支撐。

1 承載拱范圍確定方法

根據J.Talober、H.Kastner等給出的隧道在彈塑性應力狀態下的應力分布圖(圖1，圖中σθ、σr、r、P0分別為圍巖切向應力、圍巖徑向應力、距洞壁距離和初始地應力)[7]，隧道開挖后，隧道開挖空間圍巖應力解除，圍巖應力釋放向圍巖深部轉移，并逐漸恢復到初始地應力狀態。在應力重分布的過程中，圍巖出現塑性區,根據塑性區內應力高低，又可將塑性區分為兩部分：塑性區的內圈應力低于初始地應力，所對應的區域為“松動區”；塑性區的外圈應力高于初始地應力，與圍巖彈性區中應力升高部分合在一起稱作“承載區”。

承載拱本身為“承載區”，其范圍為切向應力增高區，如圖1。參考多數學者認同的承載拱邊界確定方法[9-11]，本文選取圍巖切向應力由小于初始切向應力恢復到初始地應力值時為承載拱的內邊界，圍巖切向應力恢復到與初始地應力的差值小于初始地應力的10%時為承載拱的外邊界。

圖1 隧道圍巖彈塑性應力分布及承載拱邊界示意圖

2 基于強度應力比的擠壓性圍巖隧道承載拱范圍理論解

2.1 圓形隧道圍巖彈、塑性區應力

考慮圓形隧道受雙向等壓受力狀態，施作支護后，圍巖變形受到支護限制，支護對圍巖產生抗力，圍巖進入三次應力狀態。如圖2所示，雙向等壓的初始地應力為P0，支護抗力Pi均勻分布，圓形隧道半徑R0，塑性區半徑為Rp，塑性區圍巖徑向應力、切向應力分別為σrp、σθp，圍巖徑向應力、切向應力分別為σre、σθe。

圖2 雙向等壓圓形隧道計算模型

通過單元體靜力平衡分析，可求得塑性區圍巖應力表達式分別為:

(1)

式中：σrp為塑性區圍巖徑向應力；σθp為塑性區圍巖切向應力；c為圍巖黏聚力；φ為圍巖內摩擦角；Pi為支護抗力；R0為隧道洞徑；r為計算點距隧道中心的距離。

三次應力彈塑性狀態下塑性區半徑Rp的表達式為：

(2)

式中：Rp為塑性區半徑；P0為原巖應力。

彈性區圍巖徑向應力與切向應力表達式分別為：

(3)

式中：σre為彈性區圍巖徑向應力；σθe為彈性區圍巖切向應力。

2.2 圍巖承載拱內、外邊界

由圍巖承載拱確定方法，可得承載拱內、外邊界的邊界條件為

(4)

聯立式(1)、式(3)、式(4)可得出三次應力狀態下的承載拱內、外邊界為

(5)

式中：R內、R外分別為圍巖承載拱內、外邊界距隧道中心的距離；ξ為摩爾-庫倫強度線斜率，ξ=(1+sinφ)/(1-sinφ)。

2.3 基于強度應力比的擠壓性圍巖隧道承載拱理論解

在擠壓性圍巖隧道設計施工中，以變形分級為基礎的控制理念已逐漸被人們所接受，且多以圍巖強度應力比Gn為主要指標建立變形分級標準[1-3]。在《鐵路擠壓性圍巖隧道技術規范》[1]中，依據圍巖強度應力比將變形分為輕微、中等、強烈三個等級。進一步考慮到超大埋深、極高地應力條件，將擠壓性圍巖隧道變形劃分為輕微、中等、強烈、極強烈四個等級，如表1所示[1,4]。

表1 擠壓性圍巖隧道變形等級劃分標準

圍巖強度應力比Gn為

(6)

式中：σc為圍巖強度，σc=2ccosφ/(1-sinφ)。

聯立式(5)與式(6)，可得出擠壓性圍巖隧道圍巖承載拱拱內、外邊界為

(7)

(8)

式中：Pi/P0為支護抗力比，其值等于支護抗力與初始地應力的比值。

則圍巖承載拱厚度D為：

D=R外-R內

(9)

3 擠壓性圍巖隧道承載拱厚度變化規律研究

由式(7)～式(9)可見，擠壓性圍巖隧道圍巖承載拱范圍與隧道洞徑R0、強度應力比Gn、摩爾-庫倫強度線斜率ξ、支護抗力比Pi/P0等因素有關。其中強度應力比Gn為綜合指標，可反映巖體強度、地應力、隧道埋深、圍巖重度等。在單因素分析時，取其他因素不變條件下進行該因素影響規律分析，圍巖計算參數c、φ根據我國現行規范建議取值[15]；圍巖強度σc按式(6)計算；初始地應力P0按自重應力取值，即P0=γH(γ為圍巖重度，H為隧道埋深)。

3.1 工況選取

取隧道埋深H=300 m，圍巖重度γ=20 kN/m3，圍巖黏聚力c=0.2 MPa，內摩擦角φ=23°時，通過改變洞徑及強度應力比，計算得出承載拱厚度隨強度應力比、洞徑及支護抗力比的變化規律；取圍巖重度γ=20 kN/m3，支護抗力比Pi/P0=0.05，隧道洞徑R0=7 m時，通過改變圍巖強度參數，計算得出承載拱厚度隨圍巖強度、埋深及初始地應力的變化規律。

3.2 承載拱厚度隨圍巖強度應力比的變化規律

支護抗力比考慮Pi/P0=0.05時，承載拱厚度與圍巖強度應力比的關系如圖3所示。

圖3 承載拱厚度隨圍巖強度應力比的變化曲線

由圖3可見，承載拱厚度隨圍巖強度應力比的減小而增大，呈拋物線分布形態；一般軟巖(Gn>0.3)變化幅度小，擠壓性圍巖(Gn<0.3)變化幅度大；對于Gn>0.5的一般圍巖，承載拱厚度基本不變；對于Gn<0.15的變形潛勢為強烈、極強烈的擠壓性圍巖，承載拱厚度隨強度應力比的減小而急劇增大；變形潛勢越強烈，承載拱厚度變化越大，充分說明圍巖越差，產生應力重分布的圍巖范圍越大，需要調動的參與承載的圍巖范圍越大。

3.3 承載拱厚度隨隧道洞徑的變化規律

通過改變不同隧道洞徑R0，得出承載拱厚度與隧道洞徑的關系如圖4所示。

由圖4可見，承載拱厚度隨隧道洞徑增大而增大，呈線性分布形態，說明隧道洞徑越大，需要調動的參與承載的圍巖范圍越大；不同強度應力比條件下，承載拱厚度隨隧道洞徑的變化曲線斜率基本一致。

圖4 承載拱厚度隨隧道洞徑的變化曲線

3.4 承載拱厚度隨支護抗力的變化規律

通過改變不同支護抗力比Pi/P0，得出不同強度應力比條件下承載拱厚度與支護抗力的關系如圖5所示，不同支護抗力條件下承載拱厚度與強度應力比的關系如圖6所示。

圖5 不同強度應力比的承載拱厚度-支護抗力比曲線

圖6 不同支護抗力比的承載拱厚度-強度應力比曲線

由圖5可見，相同強度應力比條件下，承載拱厚度隨支護抗力比減小而增大；強度應力比越小，承載拱厚度變化越顯著。由圖6可見，相同支護抗力條件下，承載拱厚度隨強度應力比減小而增大；支護抗力越小，承載拱厚度變化越顯著，毛洞無抗力條件下，承載拱厚度最大。通過增大支護剛度而提高支護抗力，可有效降低承載拱范圍，從而提高圍巖穩定性。

3.5 承載拱厚度隨圍巖強度的變化規律

由圖7可見，承載拱厚度隨圍巖內摩擦角和黏聚力的減小而增大。

圖7 承載拱厚度隨圍巖強度參數的變化曲線

由圖8可見，承載拱厚度隨圍巖強度的減小而增大；圍巖強度應力比越小，承載拱厚度變化越劇烈。說明在初始地應力一定的條件下，通過地層注漿加固改善圍巖強度指標，可有效降低圍巖承載拱范圍，從而提高圍巖穩定性，圍巖越差，注漿加固的必要性越高。

圖8 承載拱厚度隨圍巖強度的變化曲線

3.6 承載拱厚度隨初始地應力的變化規律

由圖9可見，承載拱厚度隨隧道埋深增大而增大；圍巖強度越小，承載拱厚度變化越顯著；隧道埋深越小，承載拱厚度變化越顯著。由圖10可見，承載拱厚度隨初始地應力的增大而增大，強度應力比越小，承載拱變化越顯著。

圖9 承載拱厚度隨隧道埋深的變化曲線

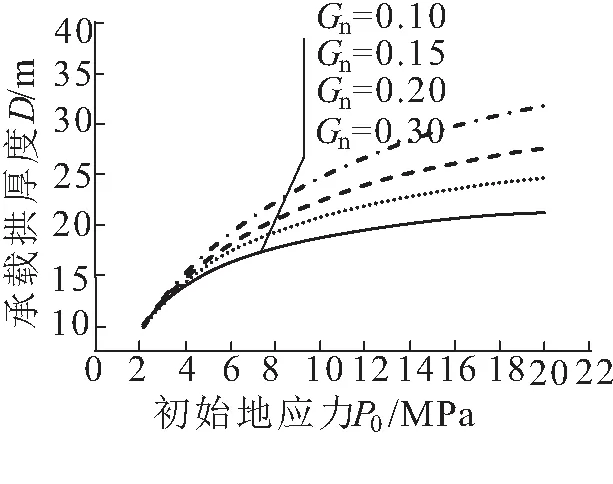
圖10 承載拱厚度隨初始地應力的變化曲線

4 結論

(1)推導了基于強度應力比的擠壓性圍巖隧道承載拱范圍的理論解，建立了圍巖承載拱厚度與擠壓性圍巖隧道變形等級的定量關系。

(2)對于一般軟巖隧道，承載拱厚度隨圍巖強度應力比的變化不明顯；對于擠壓性圍巖隧道，承載拱厚度隨圍巖強度應力比的降低而顯著增大；擠壓性圍巖隧道變形潛勢越強烈，承載拱厚度變化幅度越大，需要調動的參與承載的圍巖范圍越大，隧道變形越大，圍巖越不穩定。

(3)隧道洞徑越大，承載拱厚度越大，承載拱厚度隨隧道洞徑呈線性增長趨勢。

(4)承載拱厚度隨支護抗力的減小而增大；強度應力比越小，承載拱厚度變化越顯著；通過增大支護剛度而提高支護抗力，可有效降低承載拱厚度，從而提高圍巖穩定性。

(5)承載拱厚度隨圍巖強度的減小而增大；擠壓性圍巖變形潛勢越劇烈，承載拱隨圍巖強度的變化越顯著；通過地層注漿加固改善圍巖強度，可有效降低圍巖承載拱范圍，從而提高圍巖穩定性，圍巖越差，注漿加固的必要性越高。

(6)承載拱厚度隨隧道埋深和初始地應力的增大而增大；圍巖強度應力比越小，承載拱變化越顯著。