兩種水庫庫容計算方法的比較分析
李 浩,許 霞,李凌云
(1.山東省水利科學研究院,山東 濟南 250014;2.濟南市萊蕪區水利工程服務中心,山東 濟南 250022;3.南京師范大學地理科學學院,江蘇 南京 210034)
準確掌握水庫庫容情況是保證水庫正常運行的前提。本文基于日照市青峰嶺水庫的庫底高程實測點數據,應用等高線法和離散點法分別計算水庫庫容,并與傳統人工斷面法計算結果進行對比分析,驗證這兩種方法應用于水庫庫容計算的可靠性和精確度。
1 兩種水庫庫容計算方法
應用傳統人工斷面法施測獲得的日照市青峰嶺水庫庫底點位三維坐標原始數據,分別采用兩種不同方法對各高程下的庫容量進行計算,并將計算結果與傳統人工斷面法計算得到的結果進行比對
1.1 等高線法
該算法以DWG 格式的等高線圖為數據依據,等高線圖是根據所有測量點的三維坐標成果繪制的。
1)數據預處理。由于等高線圖中存在重疊(同一等高線存在兩條),因此,在依據等高線生成三角面片時,首先對重疊的等高線進行處理,相同的等高線只能保留一條。處理過程如下:(1)提取所有等高線的數據;(2)計算每條等高線的周長和所圍成的面積;(3)比較各等高線的面積和周長,若存在面積和周長相等的等高線,則只保留一條。
2)庫底三角網面生成算法。程序框圖如圖1所示(其中:xmin為等高線的最小 z 坐標,xmax為等高線的最大z 坐標,h 為步長)。
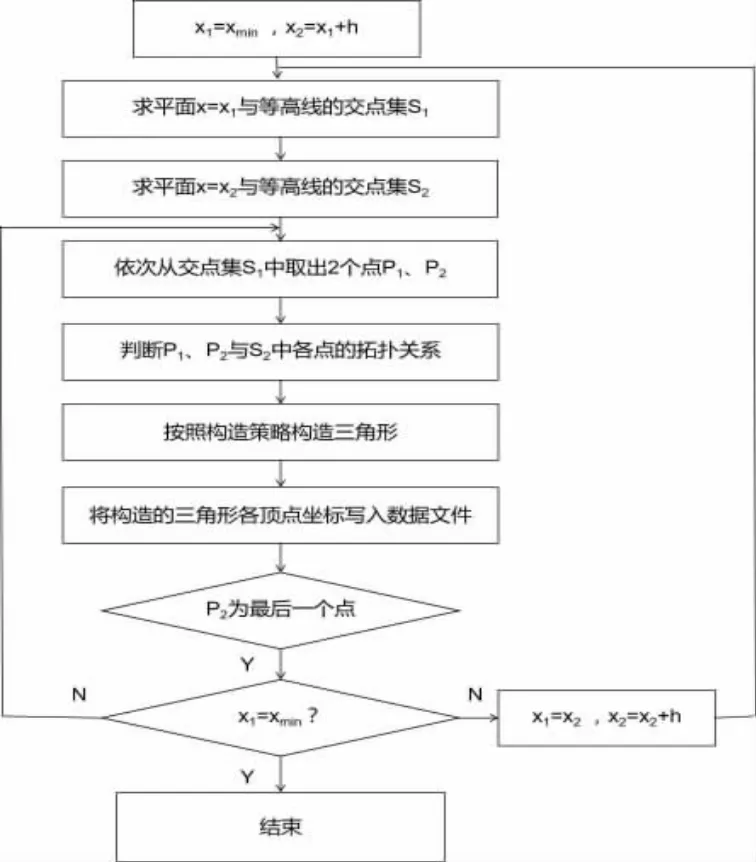
圖1 等高線法程序框圖
1.2 離散點法
該算法以測量出的庫底離散坐標點為計算依據,直接將離散點轉換成三角網面。
1)三角網面構造。通過前處理程序測量數據重合點剔除,采用Bowyer-Watson 算法實現庫底三角網面的生成。該算法的基本程序是:(1)構造一個初始超級三角形,讓這個三角形含括一切散點;(2)將集中的散點按順序插入,如圖 2(a);(3)在三角形鏈表中找到其外接圓包含該插入點的三角形,如圖 2(b);(4)然后去除影響三角形的公共邊,如圖 2(c);(5)將插入點與影響三角形的頂點全部連接起來,如圖2(d)。進而完成一個點在三角形鏈表中的植入;(6)將新形成的三角形移入進三角形數組;(7)循環執行第2 步操作,直到全部散點植入完成。
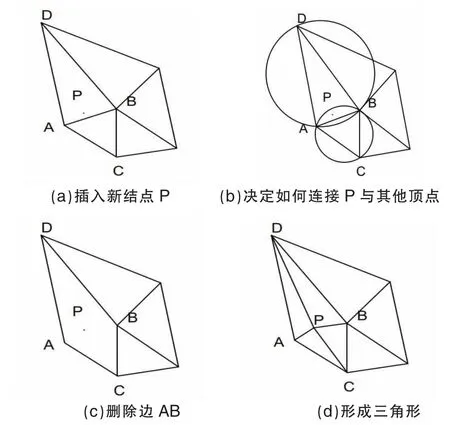
圖2 Bowyer-Watson 算法過程
離散點法程序框圖見圖3。
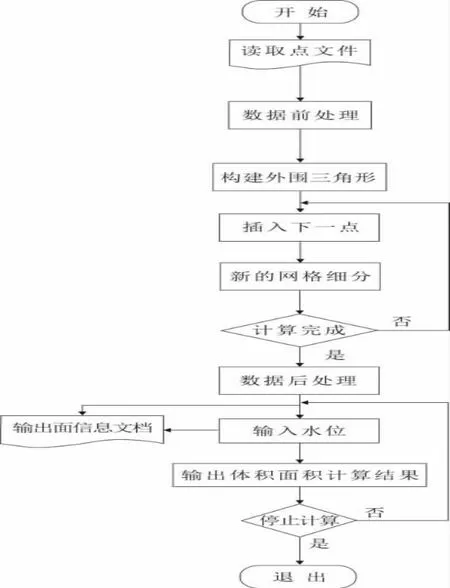
圖3 離散點法程序框圖
該算法邏輯嚴密、唯一性好,并且在構建網格的過程中,當需要增加新點時,僅僅對新點的影響三角形范圍開展局部聯網,不用對所有的點開展重新構網的操作,算法上容易實現并且不易出錯。
2)庫容計算。庫底形狀構造完成后,形成含有所有三角形頂點坐標的數據文件,根據該數據文件,可以進行庫容量、水面面積、淹沒線的計算。
設 Z 為庫面高程(庫面的 z 坐標),ΔABC 為所構建的庫底中的某一三角形,并設A 點高于B點,B 點高于C 點,即:ZA≥ZB≥ZC(ZA表示A 點的Z 坐標,其余相同),則在某一高程值Z 時,ΔABC所對應的庫容(體積)及水面面積的計算分下面四種情況(見圖4):
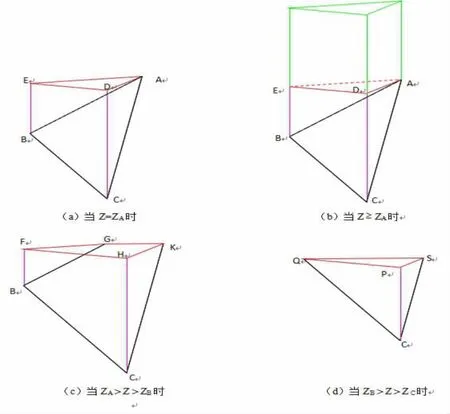
圖4 體積計算時的4 種情況
(1)當 Z=ZA時:如圖 4(a)所示,E、D 點與 A點等高,且分別與B、C 點具有相同的x、y 坐標,則ΔABC 所對應的庫容(體積)為多面體ABCDE的體積,ΔABC 所對應的水面面積為ΔADE 的面積,該三角形不存在對應的淹沒線。
(2)當 Z≥ZA時:如圖 4(b)所示,ΔABC 所對應的庫容(體積)為多面體ABCDE 的體積與以ΔABC 為底面的三棱柱的體積之和,ΔABC 所對應的水面面積為ΔADE 的面積,該三角形不存在對應的淹沒線。
(3)當 ZA>Z>ZB時:如圖 4(c)所示,ZF=ZG=ZH=ZK,點的ΔABC 所對應的庫容(體積)為多面體ABFGHK 的體積,ΔABC 所對應的水面面積為四邊形FGHK 的面積,直線GK 為該三角形對應的淹沒線。
(4)當 ZB>Z>ZC時:如圖 4(d)所示,ZD=ZQ=ZS=Z,點的ΔABC 所對應的庫容(體積)為四面體CPQS 的體積,ΔABC 所對應的水面面積為ΔPQS的面積,直線QS 為該三角形對應的淹沒線。
2 計算結果比較分析
兩種方法的計算結果如表1 所示。表1 中的誤差是指等高線法、離散點法的計算結果相對于傳統人工斷面法計算數據的偏差。可以看出,兩種計算方法得到的結果與傳統人工斷面法計算結果偏差在可接受范圍內,其中離散點法和傳統人工斷面法計算結果非常接近,等高線法相對于傳統人工斷面法計算結果的誤差略大。這是因為等高線是根據所測得的離散點生成的,在生成等高線的過程中存在著擬合誤差。由此可以得出:兩種方法應用于水庫庫容計算是可靠的,且離散點法的計算精度更高。

