淺析巧解隱圓的典型題

張?jiān)其h

(廣東省惠州市惠陽區(qū)第一中學(xué) 516211)

對(duì)于初中平面幾何問題，學(xué)生會(huì)傾向于構(gòu)建直線型模型來轉(zhuǎn)化條件，習(xí)慣利用三角形、四邊形的知識(shí)來解決問題，從而輔助線的添加就被局限在直線型里.實(shí)際上利用曲線型輔助線，在一些特定條件下，更有利于條件的集中與拓展，而圓是曲線型輔助線的代表.利用圓，構(gòu)建隱圓模型，可以使圖形的條件更豐富，通過下面六種構(gòu)建隱圓模型解題方法的對(duì)比，讓學(xué)生感受構(gòu)建隱圓模型解題的獨(dú)特，從而激發(fā)學(xué)生對(duì)數(shù)學(xué)的興趣和求知欲.

一、利用圓的定義構(gòu)建隱圓模型

例1如圖1，在Rt△ABC中，∠C=90°，AC=7，BC=8，點(diǎn)F在邊AC上，并且CF=2，點(diǎn)E為邊BC上的動(dòng)點(diǎn)，將△CEF沿直線EF翻折，點(diǎn)C落在點(diǎn)P處，求點(diǎn)P到邊AB距離的最小值是多少？

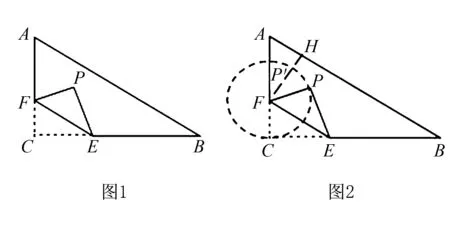
分析因點(diǎn)E是動(dòng)點(diǎn)，導(dǎo)致EF，EC，EP都在變化，但是FP=FC=2不變，所以點(diǎn)P到點(diǎn)F的距離永遠(yuǎn)等于2.根據(jù)圓的定義構(gòu)建隱圓模型，可知點(diǎn)P在以F為圓心的圓周上運(yùn)動(dòng).

解析因?yàn)椤鰿EF沿直線EF翻折，可知△CEF≌△PEF，所以FP=FC=2，點(diǎn)P在以F為圓心的圓周上運(yùn)動(dòng).過點(diǎn)F作FH⊥AB于點(diǎn)H，交⊙F于點(diǎn)P′,則FP′=FP=FC=2.

所以當(dāng)點(diǎn)P位于點(diǎn)P′位置時(shí)，線段PH取得最小值.

由∠A=∠A,∠AHF=∠C=90°，知△AFH∽△ABC.

所以AF∶FH∶AH=AB∶BC∶AC=5∶4∶3.

又因?yàn)锳F=5，所以FH=4.所以點(diǎn)P到邊AB距離的最小值為P′H=FH-FP′=4-2=2.

二、利用“直角所對(duì)的弦是圓的直徑”構(gòu)建隱圓模型

例2 如圖3，在矩形ABCD中，AB=4，BC=6，點(diǎn)E是矩形內(nèi)部的一個(gè)動(dòng)點(diǎn)，且AE⊥BE，求線段CE的最小值為多少.

分析利用AE⊥BE可構(gòu)建隱圓模型，即點(diǎn)E在以AB為直徑的⊙O上.

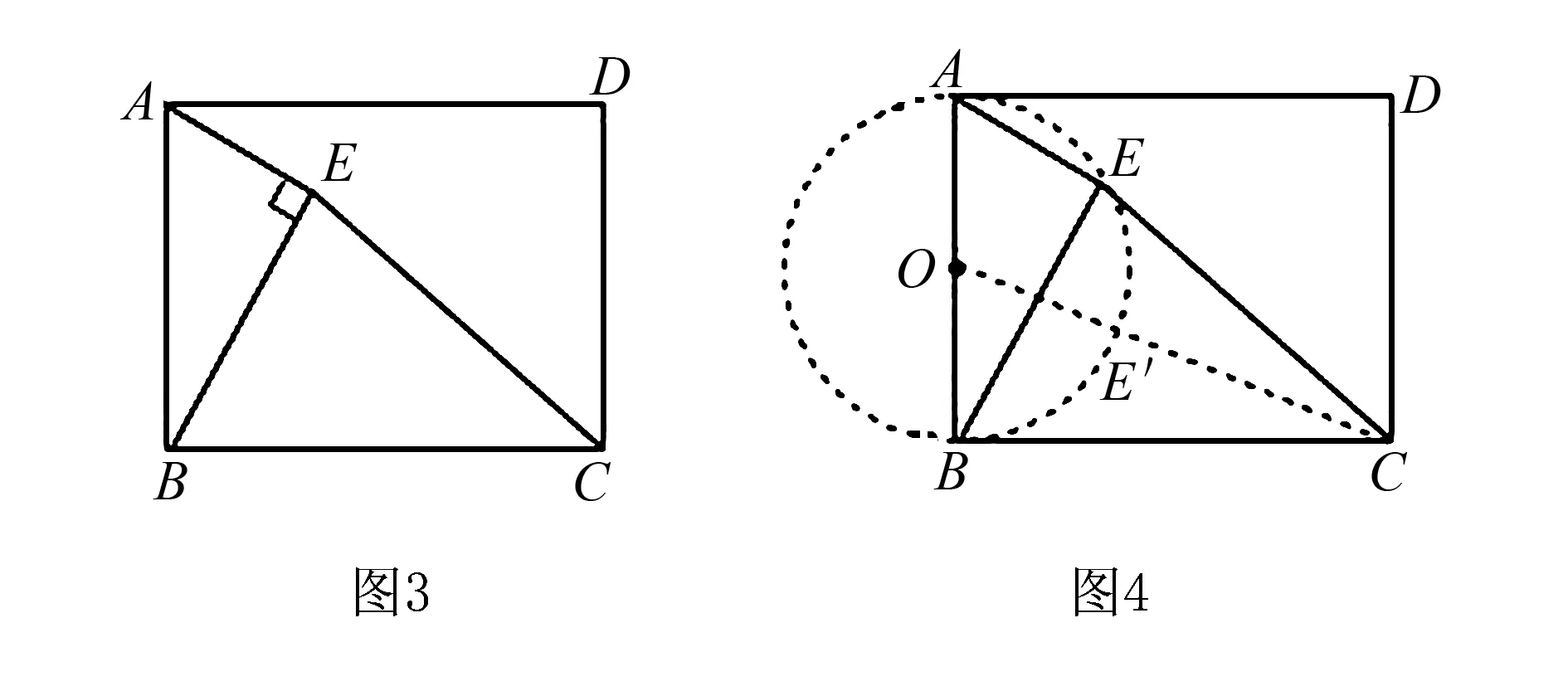
解析如圖4所示，因?yàn)锳E⊥BE，所以點(diǎn)E在以AB為直徑的半⊙O上.連接CO交⊙O于點(diǎn)E′，所以當(dāng)點(diǎn)E位于點(diǎn)E′位置時(shí)，線段CE取得最小值.

因?yàn)锳B=4，所以O(shè)A=OB=OE′=2.

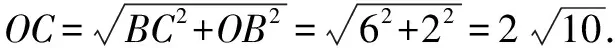
三、利用“四點(diǎn)共圓”構(gòu)建隱圓模型

例3 如圖5，△ABC中，∠ACB=90°，AC=6，BC=8，O為AB的中點(diǎn)，過O作OE⊥OF，OE,OF分別交射線AC,BC于點(diǎn)E,F，求EF的最小值為多少？

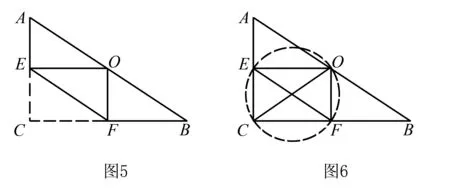
分析因?yàn)椤螮OF=90°，∠C=90°，所以點(diǎn)C，O，E，F(xiàn)四點(diǎn)共圓.因?yàn)镋F是圓的直徑，點(diǎn)O，C均在圓上，且OC長(zhǎng)度固定，要使得EF最短，則圓最小，要使圓最小，由于OC為固定長(zhǎng)度，則OC為直徑時(shí)，圓最小.

四、利用“定弦對(duì)定角”構(gòu)建隱圓模型

例4 (2017年威海)如圖7，△ABC為等邊三角形，AB=2．若P為△ABC內(nèi)一動(dòng)點(diǎn)，且滿足∠PAB=∠ACP，求線段PB長(zhǎng)度的最小值為多少？

分析因?yàn)锳C=2定弦、∠APC=120°定角，所以利用“定弦對(duì)定角”構(gòu)建隱圓模型，點(diǎn)P在圓周上，當(dāng)B，P，O三點(diǎn)共線時(shí)，BP最短.

五、確定等腰三角形的存在性構(gòu)建隱圓模型

例5 在平面直角坐標(biāo)系中，已知點(diǎn)A(2，3)，在坐標(biāo)軸上找一點(diǎn)P，使得△AOP是等腰三角形，則這樣的點(diǎn)P共有____個(gè)．

分析先分類：①OA=OP；②PO=PA；③AO=AP.

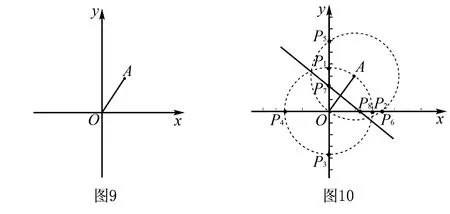
①OA=OP：以O(shè)為圓心，以O(shè)A為半徑畫弧，與坐標(biāo)軸交于P1,P2,P3,P4四個(gè)點(diǎn)，如圖10.

②PO=PA：OA的垂直平分線與x軸、y軸的交點(diǎn)分別為點(diǎn)P7,點(diǎn)P8，如圖10.

③AO=AP：以點(diǎn)A為圓心，以AO為半徑畫弧，與x軸、y軸的交點(diǎn)分別為點(diǎn)P5、點(diǎn)P6，如圖10.

解析如圖10所示，符合題意的點(diǎn)共有8個(gè)點(diǎn)．

本題考查了等腰三角形、圓的基本性質(zhì)等，解答此題的關(guān)鍵在于構(gòu)建隱圓模型，確定等腰三角形的存在性.

六、確定直角的存在性構(gòu)建隱圓模型

例6 如圖11，矩形CDEF是由矩形ABCG(AB

分析要判斷直角頂點(diǎn)的個(gè)數(shù)，只要判定以AE為直徑的圓與線段BD的位置關(guān)系即可，相交時(shí)有2個(gè)點(diǎn)，相切時(shí)有1個(gè)，外離時(shí)有0個(gè)，不會(huì)出現(xiàn)更多的點(diǎn).

解析如圖12所示，符合題意的點(diǎn)共有2個(gè)點(diǎn)．

本題主要是根據(jù)直徑所對(duì)的圓周角是直角，把判定頂點(diǎn)的個(gè)數(shù)問題，轉(zhuǎn)化為直線與圓的位置關(guān)系的問題來解決，即圓與直線BD相交，則直角頂點(diǎn)P的位置有兩個(gè).

綜上所述，通過六種構(gòu)建隱圓模型解題方法的對(duì)比，對(duì)有代表性的例題進(jìn)行分類剖析、解答，讓學(xué)生感受構(gòu)建隱圓模型解題的獨(dú)特，進(jìn)而能切實(shí)有效地提高學(xué)生的數(shù)學(xué)解題能力,進(jìn)一步開拓學(xué)生的數(shù)學(xué)思維水平.