基于像方誤差的線陣影像幾何定標模型分析
李 凱,馮世德*
(1.軍事科學院系統工程研究院,北京 100071)
衛星成像系統精確的幾何參數是遙感測繪衛星發揮應用價值、提供高精度地理信息產品的基礎[1]。法國空間中心利用分布于全球的20多個檢校場,將SPOT-5衛星的幾何參數分為靜態參數和動態參數分步檢校,實現了SPOT-5衛星的高精度定位[2-3]。IKONOS衛星建設了多處檢校場用于幾何定標[4-5]。日本ALOS Prism衛星利用地面定標場控制點對線陣CCD進行嚴格內定標[6-8]。美國OrbView3影像利用影像匹配得到的密集控制點對相機內方位元素進行標定[9]。王建榮[10]等對我國天繪一號衛星的內外定標參數進行了整體標定,定標后影像無地面控制平面和高程定位精度分別達到了10.3 m 和5.7 m。孟偉燦[11]等分別對天繪衛星高分辨率影像外部和內部誤差進行了補償,補償后影像定位精度均優于2 m。
本文首先分析了線陣推掃式相機中外部和內部定標參數對像點定位誤差的影響;然后設計了不同參數的檢校方法,逐個解算各定標參數的數值;最后利用多景影像對內外定標參數解算結果的可靠性與適用性進行驗證。
1 線陣影像在軌幾何定標模型
根據參考文獻[12]、[13],星載TDI CCD推掃式相機嚴格幾何模型可表示為:

式中,(X,Y,Z)為CGCS2000坐標系下的地面點坐標;(XGPS,YGPS,ZGPS)為CGCS2000坐標系下的相機投影中心坐標;(x,y,-f)為像點在相機坐標系下的坐標;f為相機主距;(dx,dy,dz)為衛星本體坐標系下相機投影中心與GPS相位中心的位置偏移;為相機在本體坐標系中安裝角構成的旋轉矩陣;為衛星本體坐標系到CGCS2000坐標系的旋轉矩陣;m為比例系數。
1.1 外定標參數模型
對外部誤差進行補償的方式一般包括兩種方式。
1)首先,將式(1)轉化為共線條件方程,即

然后,分別對外方位線元素(X,Y,Z)和角元素(ω,φ,κ)(ai,bi,ci,i=1,2,3為ω,φ,κ的函數)進行建模。
2)引入偏置矩陣Roffset對外部誤差統一補償,即

式中,ω、φ、κ為X-Y-Z轉角系統的3個旋轉角。
3個旋轉角隨時間變化還存在一階和二階誤差,因此對3個旋轉角進行拓展,則有:

式中,line為線陣影像掃描行號,代表時間;ω0、φ0、κ0為角元素常差項;ω1、φ1、κ1為角元素一階項;ω2、φ2、κ2為角元素二階項。
1.2 內定標參數模型
根據相機內部誤差各項參數的物理含義構建線陣影像內定標模型,即

式中,(Δx0,Δy0)為主點偏移和CCD平移;k1、k2為 鏡頭徑向畸變系數;P1、P2為鏡頭偏心畸變系數;θ為CCD線陣旋轉角;sy為CCD尺度變化因子;=x?x0;。
由于為常數,對式(6)進行變換得到:

式中,為各像元沿陣列方向坐標,是像元列號sample 的線性函數。
此外由于≈0,可建立線陣影像內部畸變的指向角模型,即
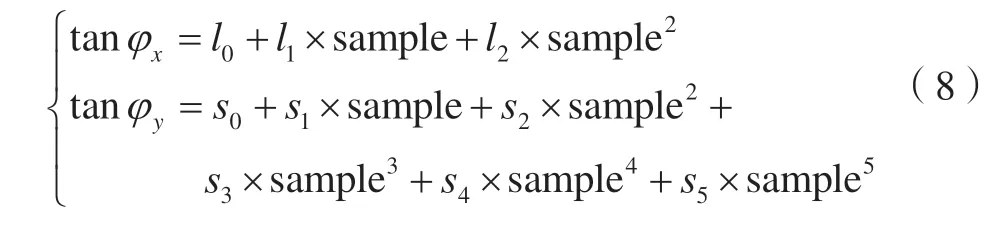
2 線陣影像像點定位誤差分析
2.1 外定標參數對像點定位的影響
圖1a中像空系的x軸指向沿軌方向,y軸指向垂軌方向,o為像主點。當外定標參數中僅存在繞沿軌方向的旋轉角ω時,線陣初始位置為圖1a中l,實際位置應為l'。將圖1a投影至s-yz平面 (圖1b)發現,ω僅造成像元列坐標的變化,變化量為dyω=cosω×y+sinω×f-y≈sinω×f。當ω中常差ω0=0、隨行號(時間)變化的一階項系數ω1=10-8時,可得到各行影像列坐標誤差隨行號變化如圖2中實線所示;當ω中ω0=ω1=0、隨行號(時間)變化的二階項系數ω2=5×10-13時,可得到各行影像列坐標誤差隨行號變化如圖2中虛線所示。
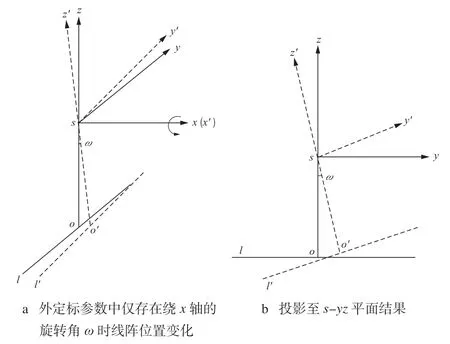
圖1 外定標參數中僅存在繞x軸旋轉角時的影響

圖2 ω存在一階和二階誤差時各行影像列坐標誤差 隨行號變化曲線
當外定標參數中僅存在繞垂軌方向的旋轉角φ時,線陣初始位置為圖3a中l,實際位置應為l',可以看出,φ僅造成像元行坐標的變化,可計算得到各像元位置行坐標變化量為dxφ=sinφ×f-x=sinφ×f。當φ為φ0=2'的常差時,同一行影像上各像元行坐標誤差約為1個像素。
當外定標參數中僅存在繞垂直于軌道平面的旋轉角κ時,線陣初始位置為圖3b中l,實際位置應為l',可以看出,κ同時造成像元行、列坐標的變化,可計算得到各像元位置行坐標誤差(沿軌方向)為dxκ= -sinκ×y,列坐標誤差(垂軌方向)為dxκ=-cosκ×y-y。由于κ角很小,因此dxκ≈0,可忽略不計。當κ為κ0=0、κ0=2'的常差時,可得到同一行影像上各像元行誤差隨列號變化的曲線如圖4a所示;當κ中常差κ0=0、κ1=10-8時,可得到各行影像行中1、6 000、12 000列像元的行坐標誤差隨行號的變化如圖4b中實線所示;當κ中κ0=κ1=0、κ2=5×10-13時,可得到各行影像中1、 6 000、12 000列像元的行坐標誤差隨行號的變化如 圖4b中虛線所示,可以看出,當κ存在一階誤差時,同一列像點的行坐標將隨行號產生線性誤差,當κ存在二階誤差時,同一列像點的行坐標將隨行號產生非線性誤差。

圖3 外定標參數中僅存在繞y軸或繞z軸旋轉角時的影響

圖4 κ存在常差、一階和二階誤差時的變化曲線
2.2 內定標參數對像點定位的影響
在式(6)中x≈0,θ很小,因此內方位元素誤差在沿軌方向較小;且即使θ較大,其與κ造成的沿軌誤差是一致的,二者具有強相關性,在外定標參數解算時該部分誤差已被改正。sy主要導致垂軌方向誤差,ds=sy×y,當sy=3e-4時,可得到線陣各像元列誤差隨列號的變化(圖5)。

圖5 sy=3e-4時像元列坐標誤差隨列號變化曲線
3 實驗結果與分析
3.1 實驗數據
實驗數據為3景天繪一號線陣傳感器正視影像,其中第一景為定標景影像,編號為123;其余兩景影像編號為124、129。124號影像與定標景影像相鄰,129號影像距離定標景影像約為300 km。3景影像位于同一軌道,大小均為12 000×12 000像素,成像時間均為2012-02-21。在定標景影像成像范圍內,利用Google Earth高分辨率衛星圖層采集了30個控制點。由于數據來源的限制,當前尚未獲得高精度的實測控制點;但從Google Earth高分辨率衛星圖層中采集的控制點具有較高的定位精度,可用于解算幾何定標參數,如ZHANG Y J[14]等利用Google Earth獲取的控制點進行幾何定標,驗證了定標結果的有效性。像點坐標為手工測量,誤差約為0.5~1個像元,控制點分布如圖6所示。其余兩景影像也采用同樣方法采集了少量控制點。

圖6 控制點在定標景影像上的分布
3.2 初始像方誤差分析
本文計算了各控制點的初始像方誤差。控制點像方沿軌殘差和垂軌殘差隨線陣行坐標(掃描時間)的變化如圖7a、7b所示;控制點像方沿軌殘差和垂軌殘差隨線陣列坐標(像元編號)的變化如圖7c、7d所示。沿軌方向和垂軌方向像點坐標的均方根誤差(RMS)如表1所示。

圖7 定標景影像初始像方誤差
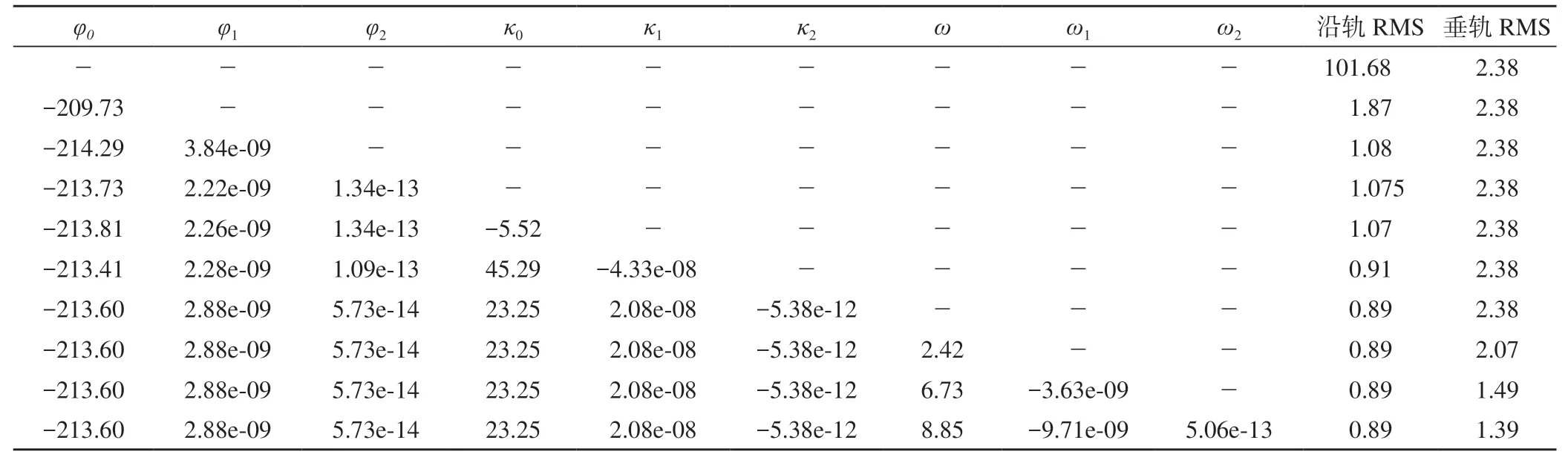
表1 對不同參數檢校后參數解算值、沿軌方向和垂軌方向的RMS
根據外定標參數對像點定位的影響,可得到:
1)圖7a中沿軌方向在起始時刻約有103個像素的系統殘差,說明外定標參數中存在旋轉角φ,且常差φ0約為2'×(-103)=-206'。
2)圖7a中沿軌方向殘差隨行坐標變化而變化,說明參數φ存在一階項φ1。
3)圖7b中垂軌方向在起始時刻約有3個像素的系統殘差,說明存在旋轉角ω,且常差ω0約為2'×3=6'。
4)圖7b中垂軌方向殘差隨行坐標變化而變化,說明參數ω中存在一階項ω1。
根據內定標參數對像點定位的影響可知,圖7d中垂軌方向殘差在列坐標中間像元附近較小,偏離像元中心越遠,殘差越大,且殘差異號,說明內定標參數存在一階項s1。
3.3 先外后內幾何定標實驗
3.3.1 外定標參數解算
僅檢校φ0后沿軌殘差隨線陣行坐標的變化如圖8a所示。表1中第2行列出了檢校得到的φ0的校正值以及檢校后沿軌方向和垂軌方向的RMS。由圖8a和表1第2行可知,檢校φ0后,沿軌方向RMS精度提升效果非常明顯,解算得到的φ0值與估計值也非常接近。同時對φ0和φ2進行檢校,檢校后沿軌方向殘差隨著行坐標(掃描時間)的變化如圖8b所示,此時沿軌方向殘差隨掃描時間的變化已不明顯。為了驗證外定標參數φ中是否存在二階誤差,同時對φ0、φ1和φ2進行檢校,檢校后沿軌方向殘差隨著行坐標(掃描時間)的變化如圖8c所示,φ0、φ1、φ2的檢校值和沿軌、垂軌方向RMS列于表1第4行。

圖8 對φ0、φ1、φ2檢校后重新計算沿軌殘差 隨線陣行坐標的變化
在消除旋轉角φ造成的沿軌方向像方誤差后,重新給出像方沿軌殘差隨線陣列坐標(像元編號)的變化,如圖9a所示,可以看出,在列坐標中間像元(像元編號6000)處的沿軌方向誤差較小,距離中心像元越遠、殘差越大,說明外定標參數κ中存在常數項κ0。本文在對φ0、φ1、φ2檢校的同時,分別對κ0、κ1、κ2進行逐個檢校,檢校結果列于表1第5~7行,對應的沿軌方向殘差分布如圖9b~9d所示。由表1和圖9可知,單獨對κ0檢校時,圖9b中沿軌方向殘差變化很小,RMS從1.075減小至1.07,改正效果不明顯;對κ0、κ1檢校后,圖9c中距離中心像元較遠的沿軌方向殘差變小,整體沿軌殘差隨列均勻分布,RMS也從 1.07減小至0.91,改正效果明顯;對κ0、κ1、κ2檢校后,圖9d中沿軌方向殘差變化很小,RMS從0.91減小至0.89,說明κ2對像方殘差的影響很小。通過上述實驗分析發現,外定標參數κ的檢校中必須包含一階 項κ1,否則難以改正κ角對像方殘差的影響。另外需要注意的是,由于κ和φ之間的相關性(均造成沿軌殘差),在檢校κ時導致φ數值變化;同時由于κ0、κ1、κ2之間較強的相關性,在檢校κ2時也將導致κ0、κ1變化。

圖9 對φ、κ0、κ1、κ2分別檢校后沿軌殘差隨線陣列坐標的變化
對φ和κ檢校后,沿軌方向的系統殘差已被消除。φ和κ檢校前后垂軌方向的RMS如表1所示,可以看出,對φ和κ的檢校均沒有改變垂軌方向殘差,這也驗證了旋轉角φ和κ主要影響像元行坐標的判斷。此時,剩余垂軌方向殘差仍如圖7b所示,其中系統殘差主要是由旋轉角ω造成的。分別對ω0、ω1、ω2進行檢校,結果列于表1的第8~10行,可以看出,對ω角中常數項ω0和一階項ω1檢校后,垂軌方向RMS明顯減小,說明ω角中存在較大的常差和一階項。ω角檢校完成后,垂軌方向殘差減小至1.39個像素,垂軌殘差隨線陣行坐標的變化如圖10a所示,可以看出,對ω角改正后垂軌方向系統殘差已被消除,垂軌殘差隨掃描行的變化均勻分布;但垂軌殘差的數值仍較大,這主要是由內定標參數誤差造成的。垂軌殘差隨像元列坐標的變化如圖10b所示,可以看出,垂軌方向殘差與圖7d非常類似,且隨列坐標的變化規律更加明顯,因此下一步需要求解內定標參數標定,以消除垂軌系統殘差。
3.3.2 內定標參數解算
根據內定標參數對像點定位的影響、對圖7d中垂軌方向殘差的分析以及圖10b中垂軌殘差隨像元列坐標的變化可知,內定標參數中應主要包括主點偏移、CCD尺度變化因子以及CCD排列旋轉角誤差。因此,本文在對外定標參數檢校后,首先檢校與這些誤差相關的參數,即式(8)中的l0、l1、s0和s1。內定標參數解算結果與沿軌、垂軌RMS列于表2第1行,可以看出,對主點偏移、CCD尺度變化因子以及CCD排列旋轉角誤差標定后,沿軌殘差和垂軌殘差均進一步減小,其中垂軌方向RMS由1.39減小至0.89,效果明顯。然后,對式(8)中所有內定標參數進行檢校,結果列于表2第2行,可以看出,沿軌方向RMS已不再變化,垂軌方向RMS由0.89減小至0.81,說明CCD尺度變化因子是內定標參數中影響定位結果最主要的因素。垂軌殘差隨列坐標的變化如圖11所示。對比 圖11和圖10b可知,內定標參數檢校后,垂軌方向殘差明顯減小,且殘差隨像元列坐標均勻分布,系統性殘差被消除。

圖10 對外定標參數改正后垂軌殘差隨線陣行、列坐標的變化

圖11 所有內、外定標參數檢校后垂軌殘差隨列坐標的變化

表2 內定標參數檢校后參數解算值、沿軌方向和垂軌方向的RMS
3.4 定標參數適用性驗證
本文利用定標景影像和定標景軌道上其他影像進行定位實驗驗證。應用定標景影像內外定標參數前后該景影像檢查點的像方定位結果如表3所示,可以看出,利用內定標參數重新定位后,定標景影像垂軌方向殘差明顯減小;利用解算得到的內外定標參數再次對檢查點進行定位,沿軌和垂軌方向的RMS均減小至1個像素左右;利用外定標參數重新定位后,沿軌方向和垂軌方向RMS均得到了有效改善,驗證了本文定標參數的有效性。

表3 應用于定標景影像實驗的內、外定標參數/像素
將內定標參數應用于124號和129號影像,并利用少量控制點對外部誤差補償,再進行像方定位實驗,定位結果如表4所示,可以看出,124號和129號影像直接定位誤差均較大,且隨著時間的推移,垂軌方向RMS有變大的趨勢;利用內定標參數重新定位后,這兩景影像垂軌方向RMS均減小了約0.4~0.5個 像素,說明內定標參數是有效的,也驗證了航天相機內部幾何結構是穩定的;利用少量控制點對兩景影像進行外部誤差補償后,取得了與定標景影像相當的定位精度,說明內定標參數已基本補償了內部 誤差。
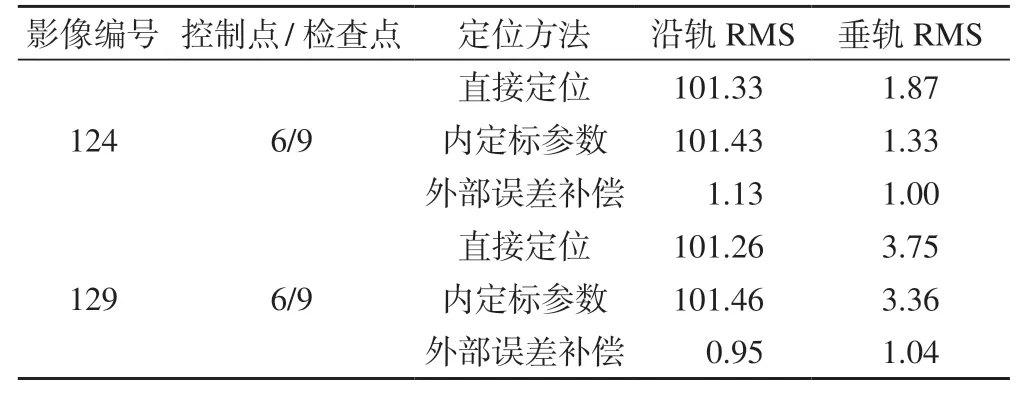
表4 應用于其他景影像實驗的內定標參數/像素
4 結 語
本文基于像方誤差對內外定標參數進行了分析,在此基礎上構建并驗證了線陣影像定標模型。將計算得到的內、外定標參數應用于定標景影像檢查點取得了較好的定位結果;將內定標參數應用于其他景影像時,達到了與定標景影像相當的定位精度。驗證實驗表明,本文采用的定標模型可計算出有效的內、外定標參數,同時驗證了航天攝影測量相機內部幾何結構的穩定性。

