基于GA-BPNN 的PM2.5 濃度預測模型
鄭俊褒,華思潔
(浙江理工大學 信息學院,浙江杭州 310016)
0 引言
隨著當前社會工業化水平的提升和自然災害發生頻率的增加,空氣質量成為越來越值得重視的問題。PM2.5濃度是衡量空氣質量的一項重要指標,它指環境空氣中空氣動力學當量直徑小于等于2.5 微米的顆粒物,對人體健康危害極大,PM2.5 所吸附的重金屬、苯并芘等致癌物、持久性有機污染物等,會經過呼吸系統進入人體,直接影響到肺,對人體造成重金屬中毒、患癌幾率上升、生殖生育危害等問題[1]。提前預測未來PM2.5 濃度可以為人們出行提供健康有效的信息[2]。
基于機器學習算法的PM2.5 濃度預測模型近年來發展迅速,張怡文等[3]利用PCA 的方法對數據進行降維,在提高預測準確率的同時,降低了時間復雜度,并將降維后的數據賦給BP 神經網絡模型以完成預測;陳志文等[4]采用openstack 云計算組件,部署大數據平臺以完善BP 神經網絡,通過自我學習提高預測準確率;Luo 等[5]基于圖像的方法,采用深度學習和機器學習擴展對PM2.5 的感知能力,構建卷積神經網絡和梯度增強機,組成端到端模型進行預測;劉林波等[6]采用遺傳算法優化后的BP 神經網絡建立PM2.5濃度預測模型,驗證其比BP 神經網絡具有更好的精度。
作為傳統經典算法,BP 神經網絡在PM2.5 濃度預測領域也有著豐富的成果[7-9],而由于其存在隨機初始權值和閾值、隱含層神經元節點數選擇具有主觀性、易陷入局部最優等缺陷,模型精度還有較大提升空間[10-11]。神經網絡的權值和閾值一般通過初始化為[-0.5,0.5]區間的隨機數而確定,該初始化參數對網絡訓練影響很大,但是又無法準確獲得[12],對于相同的初始權重值和閾值,網絡訓練結果一樣。本文引入遺傳算法就是為了優化出最優的初始權值和閾值[13],隱含層神經元節點數采用Kolmogorov 定理,設置為2n+1(n為輸入層節點數),并在一層隱含層的結構基礎上設置三層隱含層,提高特征學習能力,進一步提升PM2.5 濃度預測準確率[14-16]。
1 基于GA 的BPNN 優化算法
1.1 BP 神經網絡
20 世紀80 年代,Rumelhart&McClelland 等學者提出了一種按照誤差逆向傳播算法訓練的多層前饋神經網絡,即為目前應用最廣泛的BP 神經網絡,BP 神經網絡的基本思想是梯度下降法,利用梯度搜索技術,使得網絡的實際輸出值和期望輸出值的誤差均方差最小。
一個BP 神經網絡模型通常由一個輸入層、一個或多個隱含層、一個輸出層組成,如何設計各層之間的權重值是構建BP 網絡的重點。
近年來,BP 神經網絡以其強大的非線性映射能力和泛化性、獨特的適應性,在函數逼近、模式識別、分類問題、數據壓縮等領域均取得了豐富的成果。但同時,它也存在收斂速度慢、易陷入局部最優、網絡層數和神經元個數容易受主觀影響等問題[17-18]。
1.2 算法流程
遺傳算法是根據大自然中生物體進化規律而提出,是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型,是一種通過模擬自然進化過程搜索最優解的方法。針對BP 神經網絡易陷入局部最優的缺陷,本文利用遺傳算法的全局搜索能力優化BP 網絡的初始權重值和閾值,使優化后的預測模型能夠更好地進行訓練和測試。基于遺傳算法優化BP 神經網絡流程如圖1 所示。
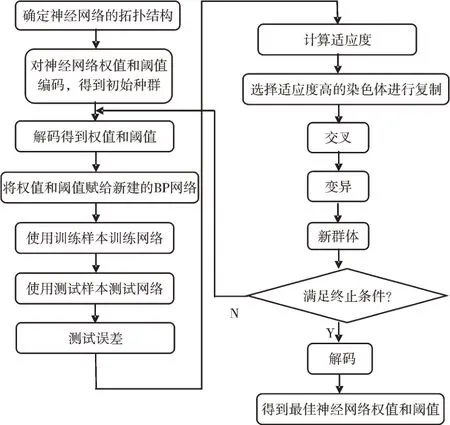
Fig.1 Algorithm process圖1 算法流程
1.3 遺傳算法實現
使用遺傳算法優化BP 神經網絡權值和閾值的主要步驟為種群初始化、適應度函數計算、選擇、交叉重組、變異、子代重插入到父代得到新種群、代計數器增加、記錄每代最優值。
(1)種群初始化。本文的網絡結構是10-21-21-21-1,權值和閾值個數如表1 所示。

Table1 Number of weights and thresholds表1 權值、閾值個數
個體編碼采用二進制編碼,每個個體均為一個二進制串,由輸入層與第一隱含層連接權值、第一隱含層閾值、第一隱含層與第二隱含層連接權值、第二隱含層閾值、第二隱含層與第三隱含層連接權值、第三隱含層閾值、第三隱含層與輸出層連接權值、輸出層閾值8 個部分組成。假定編碼為10 位二進制數,則個體二進制編碼長度為11 770。其中,1~2 100 位為輸入層與第一隱含層的連接權值編碼;2 101~2 310 位為第一隱含層閾值,依此類推。
(2)適應度函數。本文所用的適應度分配函數為:FitV=ranking(obj),obj 為目標函數的輸出。為了使預測值與實際值的殘差盡可能小,目標函數的輸出設置為測試樣本的預測值與實際值的誤差矩陣的范數。
(3)選擇、交叉重組、變異。其中,選擇算子使用隨機遍歷抽樣(sus),交叉算子使用單點交叉算子,變異是以一定概率的隨機方法選出變異基因,將其二進制編碼進行0-1交換。
2 模型構建與實驗
2.1 數據預處理
2.1.1 數據缺失值及特征化處理
本文數據預處理包括缺失值處理、特征化處理、卡方檢驗確定影響因子以及歸一化處理。
本次實驗的數據來自中國環境監測總站的全國城市空氣質量實時發布平臺,以杭州市為例,選取2020 年5 月1日至2020 年6 月20 日、時間間隔為一小時的共1 223 組數據,數據集包括PM2.5、PM10、SO2、NO2、O3、CO 濃度,其中缺失2 組,以等間距牛頓插值法補全,如式(1)所示。
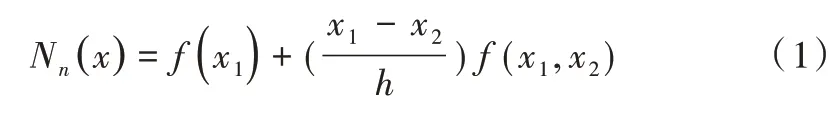
其中,h為節點間距,x1、x2分別為缺失值的前后兩個數據。
天氣相關數據來自www.k780.com 網站,它提供了包括溫度、濕度、風向、風級以及天氣狀況在內的以小時為單位采集的數據,同樣收集2020 年5 月1 日至2020 年6 月20 日之間的數據。
神經網絡無法識別文本數據,因此將數據中的風向(東北、東、東南、南、西南、西、西北、北)分別用1-8 代替,天氣狀況(晴、多云、陰、雨)分別用1-4 代替。
2.1.2 卡方檢驗確定影響因子
為確定天氣數據中哪些為PM2.5 濃度的影響因子,本文采用卡方檢驗方法得到這些數據。其中,溫度、濕度、風級和天氣狀況會影響PM2.5 的濃度。以濕度為例,進行卡方檢驗具體步驟如下:
(1)H0假設濕度與PM2.5 濃度(單位:μg/m3)無關,平均濕度(采用四舍五入,單位:%單位濕度)與PM2.5 濃度的頻數如表2 所示。

Table 2 Frequency relationship between average humidity and PM2.5 concentration表2 平均濕度與PM2.5 濃度的頻數關系
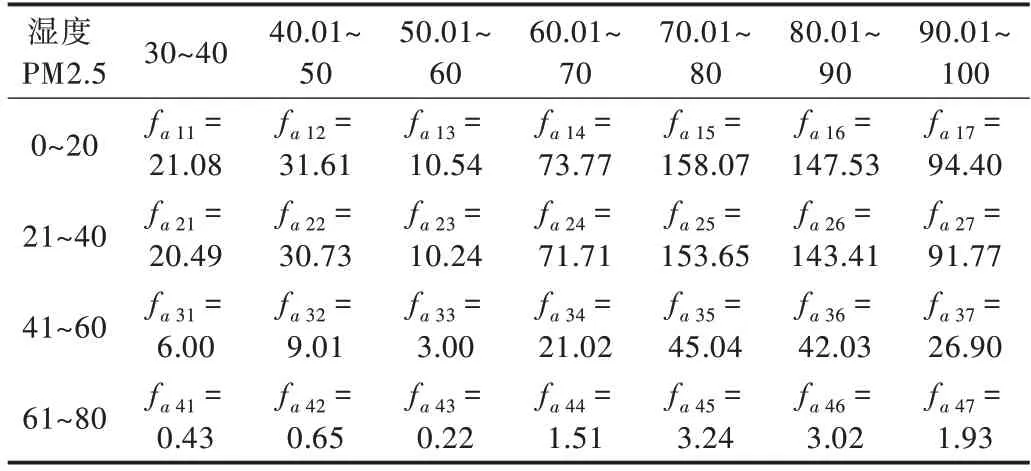
Table 3 Expected frequency of average humidity and PM2.5 concentration表3 平均濕度與PM2.5 濃度的期望頻數
(3)確定自由度(7-1)*(4-1)=18,取顯著性水平0.005,根據CHIINV(0.005,18)得到臨界值P=37.2。
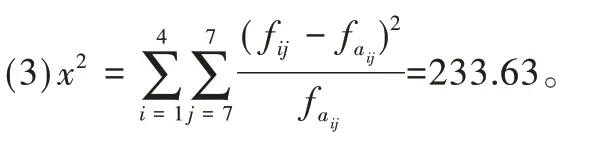
(4)因為x2>P,則拒絕原假設,即濕度與PM2.5濃度有關。
2.1.3 數據歸一化處理
由于PM2.5 濃度的各影響因子數據范圍不同,可能會影響神經網絡的訓練速度和表達能力,為提升模型效果,先對數據集進行歸一化處理,本文采用max-min 數據歸一化方法,將所有數據縮放到0-1 范圍內。
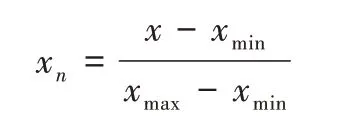
其中,x為原始值,xmax、xmin分別為該變量的最大值和最小值,xn為歸一化處理后的值。
2.2 模型構建
2.2.1 模型結構
在BP 神經網絡模型建立過程中,輸入、輸出數據的選擇會直接影響到模型性能。本文預測杭州市PM2.5 濃度變化,輸入數據層為前一時刻的PM2.5、PM10、SO2、NO2、O3、CO 濃度,以及溫度、濕度、風級和天氣狀況,輸出層為后一時刻的PM2.5 濃度。訓練數據集為前1 023 組,測試數據集為后200 組。
考慮到PM2.5 濃度預測是一個涉及時間序列的較為復雜的非線性函數,一層隱含層的擬合效果不一定能很好地達到預期效果,因此本文神經網絡模型的隱含層層數設置為三層,模型結構如圖2 所示。
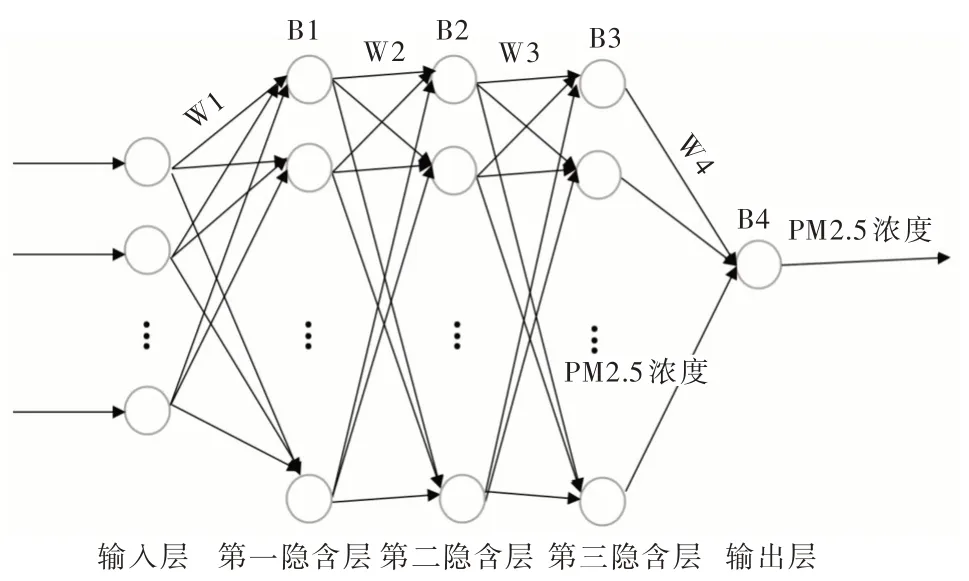
Fig.2 Neural network topology圖2 神經網絡拓撲結構
其中,wi為各層之間權重值,Bi為各隱含層與輸出層的閾值。
為了將多個線性輸入轉換為非線性關系,需要在隱含層與輸出層的輸入與輸出之間添加激勵函數,激勵函數取雙曲正切函數:
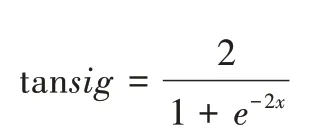
訓練函數取L-M 優化算法,即trainlm 函數,該算法對于中等規模的BP 神經網絡有著最快的收斂速度。
2.2.2 模型建立
為驗證GA-BP 神經網絡模型在PM2.5 濃度預測問題上的可操作性和有效性,在配置為64 位、內存為8GB 的Mac OS X操作系統與MATLABR2017b平臺上進行仿真實驗。
本文將遺傳算法與BP 神經網絡結合,構成GA-BPNN模型,用遺傳算法概率化的尋優方法,自適應地調整搜索方向,確定輸入層與第一隱含層、各隱含層之間、第三隱含層與輸出層的最優權重值,以及各隱含層與輸出層的最優閾值,使得原BP 神經網絡模型在預測效果上得到提升。實驗相關參數如表4、表5 所示。

Table 4 Genetic algorithm parameter setting表4 遺傳算法參數設置

Table 5 GA-BP model parameter setting表5 GA-BP 模型參數設置
3 實驗結果及分析
3.1 評價指標
本文采用的模型預測精度評價指標主要包括均方根誤差(RMSE)、平均絕對誤差(MAE)、一致性指數(IA)。均方根誤差和平均絕對誤差是衡量預測值與實際值之間的偏差,其值越小越好,一致性指數則是預測值和實際值趨勢變化的體現,越接近于1 說明變化的一致性越高。
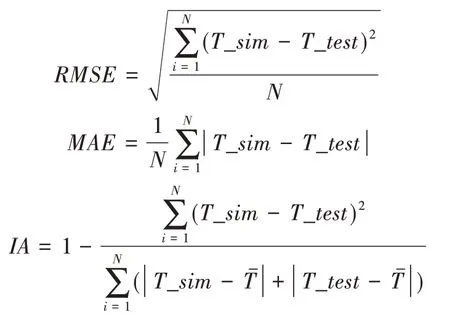
其中,N為預測樣本個數,T_sim為模型預測值,T_test為樣本實際值,為樣本實際值的平均值。
3.2 GA-BPNN 模型與比較模型預測結果分析
為驗證本文算法的可行性,使用訓練數據集分別訓練隨機權值和閾值的傳統BPNN 模型、傳統LSTM 模型、基于GA 優化后的權值和閾值的BPNN 一層隱含層模型和三層隱含層模型,預測結果如圖3—圖6 所示,4 種模型的相對誤差比較如圖7 所示。
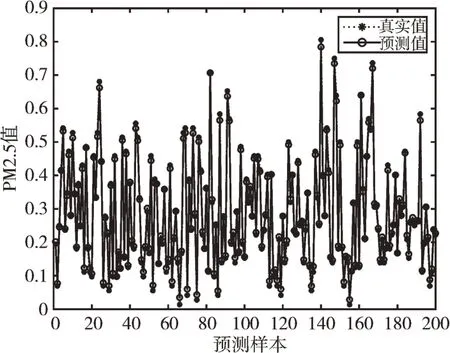
Fig.3 BPNN prediction effect圖3 BPNN 預測效果
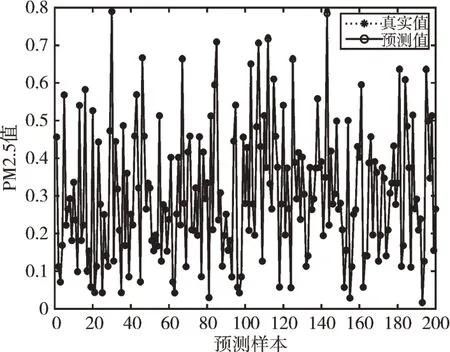
Fig.4 Traditional LSTM model prediction effect圖4 傳統LSTM 模型預測效果
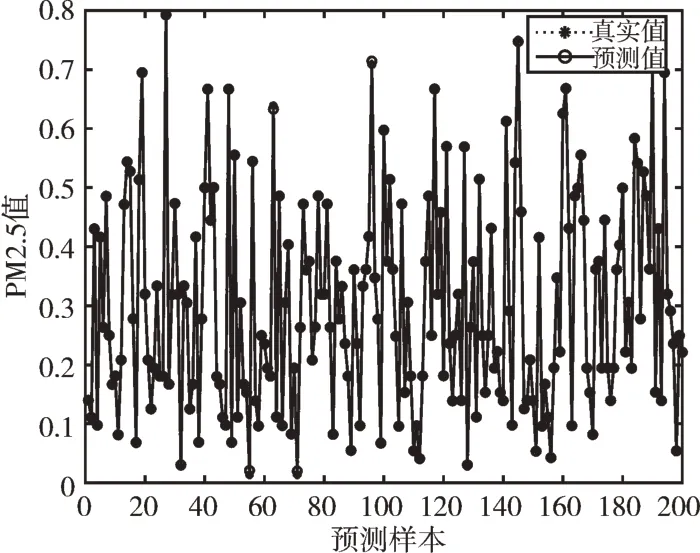
Fig.5 Prediction effect of one hidden layer of GA-BPNN圖5 GA-BPNN 一層隱含層預測效果

Fig.6 Prediction effect of three hidden layers of GA-BPNN圖6 BPNN 三層隱含層預測效果
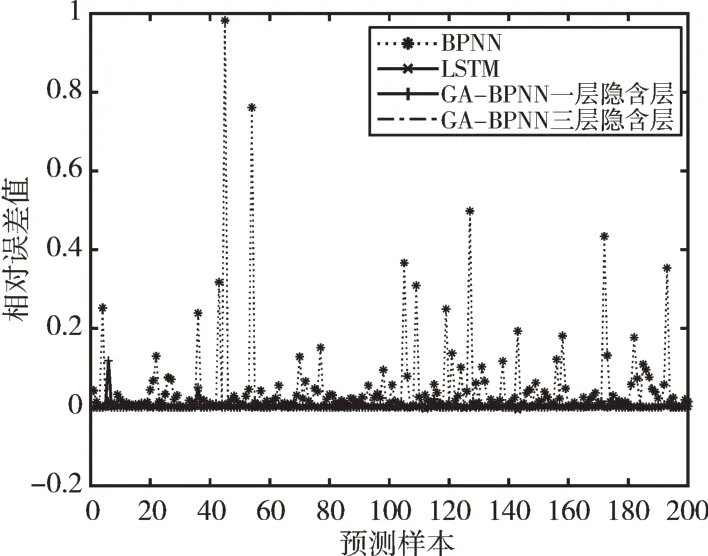
Fig.7 Comparison of the relative errors of the four models圖7 4 種模型相對誤差比較
由圖3—圖6 可以看出,GA-BPNN 模型的預測曲線比傳統BPNN 模型更為貼合,而三層隱含層的效果比一層隱含層擬合度更高,預測精度更好;由圖7 可以看出,GABPNN 模型的相對誤差值相對BPNN 模型和LSTM 模型明顯下降,說明預測效果得到提升。4 種模型的預測評價指標如表6 所示。
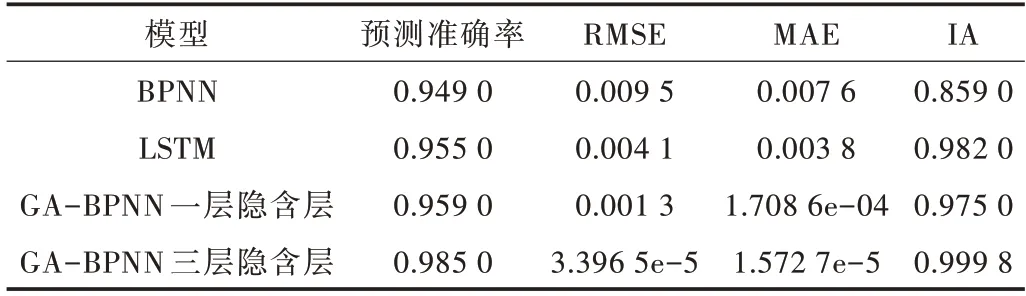
Table 6 Model evaluation index comparison表6 模型評價指標比較
可以看出,相較于傳統BPNN 模型和傳統LSTM 模型,本文GA-BPNN 模型相對于傳統BPNN 在誤差上降低了較大幅度,擬合度也得到了16.4%的提升,使用GA-BPNN 算法在運行時間上雖稍有增加,但仍在合理范圍內,說明GA-BPNN 模型針對PM2.5 濃度預測準確性較高,同時有較快的收斂速度及較好的穩定性,是一種應用前景良好的預測模型。
4 結語
PM2.5 濃度的變化會受到土壤揚塵、植物花粉、細菌、自然災害等自然源和工業燃料燃燒、交通工具尾氣排放、不完全燃燒的煙草產品等人為源因素的影響,具有很強的實時性與復雜的非線性。本文為解決BPNN 存在的易陷入局部最優的問題,將具有良好全局尋優能力的遺傳算法與強大的非線性映射能力的BPNN 相結合,提出了基于GABPNN 模型的PM2.5 濃度預測模型,用得到的最優權值及閾值進行訓練,將優化后的模型用于預測,并與傳統BPNN 模型作比較。實驗結果表明,本文算法在預測精度上有所提升,均方根誤差和平均絕對誤差降低,擬合結果更優,可以為PM2.5 濃度提供更完善的預測信息。在遺傳算法訓練過程中,迭代次數相對較高是目前存在的問題,如何提高算法收斂速度是下一步研究方向。

