改進物品相似度計算的協同過濾算法

方 惠，李 民，鄧秀輝，余開朝

（昆明理工大學機電工程學院，云南昆明 650500）

0 引言

在信息爆炸的時代，用戶難以從大量數據信息中快速精確地獲取所需信息，容易產生信息超載（Information Overload）問題［1］。為幫助用戶快速找到感興趣的產品，推薦系統應運而生。近年來，推薦系統在電影、新聞、電子商務等諸多領域中起到了重要作用，有效減輕了信息超載現象。作為推薦系統的核心部分，推薦算法成為人們研究的熱門對象［2］。目前協同過濾（Collaborative Filtering，CF）算法已經應用于互聯網的眾多領域［3-6］，其實現原理是根據用戶以往在網絡中搜索產生的數據發掘其可能喜歡的東西，根據喜好內容不同將用戶分成小組，推薦與其愛好相近的商品［7］。但該算法存在一些不足，如沒有考慮到用戶興趣會隨時間推移而發生變化，熱門物品也可能會影響相似度計算。以上問題均會導致推薦系統的精確度出現偏差，從而使用戶得不到滿意的推薦結果。

CF 算法是目前使用最廣泛、最有效的算法之一［8］，但存在推薦精確度不高等問題，許多學者對此進行了研究。董立巖等［9］在相似度矩陣的計算過程中融入時間衰減因子，使推薦結果更具時效性；尹毫等［10］提出在物品相似度計算中融入物品懲罰因子以修正物品相似度矩陣的計算，在推薦精確度方面顯著提高；熊麗榮等［11］考慮到用戶興趣會隨著時間發生變化，故采用時間效應模型函數處理用戶歷史評分數據，推薦效果明顯優于傳統算法；鄧華平［12］提出在CF 算法中加入項目聚類和時間衰減函數，加快了最近鄰居集合的尋找速度，提升了推薦精確度；崔國琪等［13］提出在物品相似度計算中融入物品懲罰因子，加入懲罰因子的CF 推薦算法在保持算法精確度的同時，可在一定程度上降低推薦結果流行度；Chen 等［14］從用戶評分角度出發，將平衡因子引入傳統的余弦相似度算法中，用于計算不同用戶間的項目評級尺度差異，提出了一種改進的基于優化用戶相似度的CF 算法，推薦精確度顯著提高；Lee 等［15］提出將偏好模型的概念應用于CF 算法中，修正用戶—物品評分舉證，有效提高了該算法的精確度和召回率。

以上改進算法僅提高了商品推薦的精確度，但未考慮到用戶興趣會隨時間推移而發生變化，亦未考慮將時間衰減函數與物品懲罰因子融合到一起。針對以上問題，本文在原有研究成果的基礎上，在傳統相似度矩陣計算中引入時間衰減函數和物品懲罰因子，得到改進相似度矩陣的推薦算法在精確度、召回率和F1 值上均比傳統CF 推薦算法明顯提高，更有利于推薦出使用戶滿意的結果。

1 理論基礎

1.1 傳統CF 算法

傳統CF 算法可分為基于用戶的推薦算法（User CF）和基于商品的推薦算法（Item CF）。User CF 算法的主要思想為尋找與目標用戶興趣相似的用戶集合，同時將該集合中用戶喜歡但沒有聽過的商品推薦給他們。Item CF 算法的主要思想為根據用戶歷史評分計算物品之間的相似度，通過物品相似度和用戶歷史行為預測用戶以往喜歡商品的相似物品［16］。傳統CF 算法的實現過程為：首先獲取歷史評分數據，構成網絡用戶—項目評分矩陣；然后計算網絡用戶或項目間的評分相似度，按照相似度對網絡用戶或項目進行排列，排列靠前的幾個用戶或項目可以被看作是鄰居，利用得到的相似度和鄰居用戶歷史評分數據計算預測評分；最后選取預測排名靠前的若干項作為推薦結果返回給目標用戶或項目，至此完成推薦［17］。

傳統CF 算法存在的不足體現在以下兩個方面：①生活中，用戶興趣會隨著時間推移而發生改變，但傳統CF 算法等同考慮商品不同時間段的評分，導致尋找近鄰用戶時推薦精確度降低；②熱門商品評價人數多，在相似度計算中會影響推薦結果的精確度。

1.2 算法改進的相似度計算

相似度矩陣在計算時分為基于用戶的相似度集合與基于商品的相似度集合。定義用戶集合U={u1,u2,…um}，商品集合I={i1,i2,…i3}，可用1 個n×m 的用戶—商品評分矩陣Hmn對商品相似度進行建模，構建的用戶—商品評分矩陣Hmn如下：

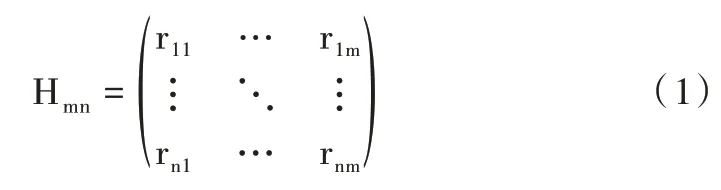
式（1）中，矩陣Hmn中的n 行代表n 個用戶，m 列代表m個商品，第n 行m 列矩陣元素rnm表示第n 個用戶對第m 個商品的評分。

項亮［18］引入熱門商品與該商品的幾何平均值以降低熱門商品與其他商品的相似度，公式如下：

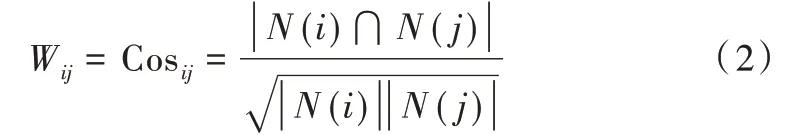
式（2）中，|N(i) |表示評價過商品i的用戶集合，|N(j)|表示評價過商品j的用戶集合，|N(i) ?N(j) |表示對商品i和商品j都有過評價的用戶集合。

推薦系統不僅要反映出用戶的近期偏好，還要預測其長期偏好。Breese 等［19］提出不活躍用戶對商品相似度的影響大于活躍用戶，因此在計算時要降低活躍用戶對相似度權重的影響，即增加項，公式如下：

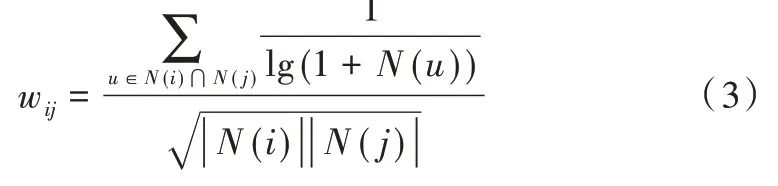
式（3）中，N(u)表示對商品u有過行為的所有用戶。

近期行為最能反映出用戶的當前興趣，因此時間相隔較短的行為才能更好地反映商品之間的相似度，故在公式（3）中加上時間衰減衰減因子［20］，公式如下：

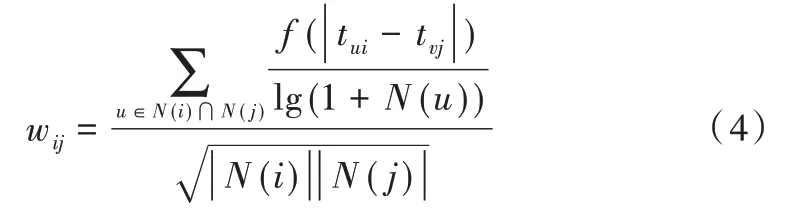
式（5）中，α為時間衰減因子的影響系數，用戶興趣變化越快，α的值越大，反之越小［21］。

由式（4）得到用戶的最近行為，由于用戶的最近行為與當前行為關系最大，因此計算用戶對商品的評分時還應加上時間衰減函數最終得到用戶u對商品j的偏好程度為：

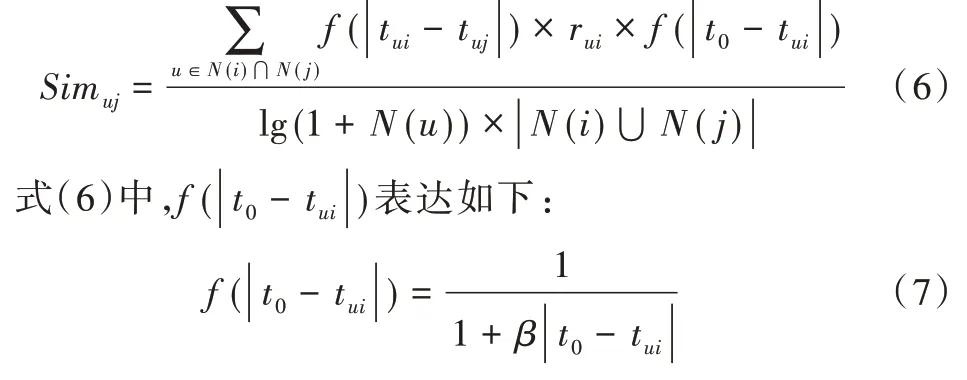
式（7）中，t0為當前時間，rui為用戶u對商品i的偏好程度，β為時間衰減因子。

2 實驗設計

對本文提出的算法與傳統CF 算法（余弦相似度）進行比較，分別在不同K 值（近鄰用戶數）和Top N 推薦長度下比較二者的精確度、召回率和F1 值，并對實驗結果進行分析。

2.1 實驗算法實現步驟

改進商品相似度算法步驟如下：

輸入：用戶—商品評分矩陣Hmn，近鄰用戶數K，商品返回數I，推薦列表長度N。

輸出：用戶推薦列表。

步驟1：在訓練集中構建用戶—商品評分矩陣Hmn。

步驟2：根據公式（3）計算加入物品懲罰因子的商品相似度矩陣wij。

步驟3：根據公式（4）加入時間衰減函數，計算用戶最近的商品相似度矩陣wij，其中參數α設置為0.5。

步驟4：根據公式（6）得到最終用戶當前對商品的相似度矩陣wij，其中參數β設置為0.8。

步驟5：遍歷用戶歷史商品集合，從該集合中找出每個歷史商品最相似的K 個商品作為候選集。

步驟6：從候選集合中選出指定返回數為I 的集合作為推薦結果。

2.2 實驗準備

以電影評分作為實驗對象，選取GroupLens 實驗室成立的MovieLens 站點中的ml-1m 數據集。如表1 所示，該數據集包含6 040 個用戶對3 900 部電影的評分記錄，其中每個用戶最少有20 條評分數據，共計1 000 209 條評分記錄。評分劃分為5 個等級，用1～5 的整數表示，評分數值越大表示該用戶對電影的喜愛程度越高。該評分數據的稀疏度為1-1 000 209/（6 040×3 900）=0.956，兩個時間衰減因子α和β分別設置為0.5 和0.8。數據集中還包含了用戶個人信息和電影標簽信息。

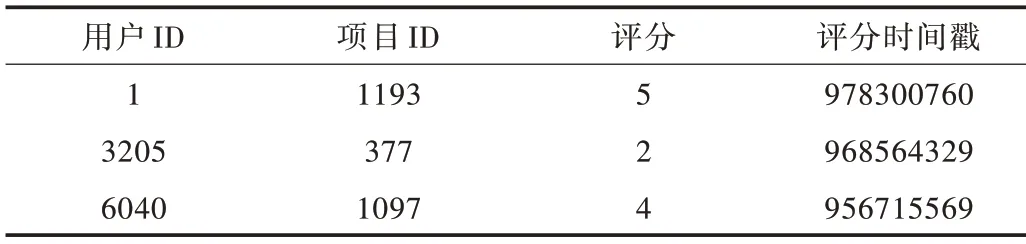
Table 1 Partial experimental data set表1 實驗數據集部分展示

2.3 推薦指標

為評價算法性能，將整個MovieLens 數據集進一步拆分為不相交的兩個部分，分別為訓練集和測試集。為此，引入變量x 作為測試集占整個數據集的百分比，設定x=0.2，即在整個數據集中，訓練集占80%，測試集占20%，訓練集與測試集比例為8∶2［22］。利用不同K 值和Top N 算法比較精確度（Precision）、召回率（Recall）和F1-Score 的變化，在3 次試驗下取評價指標的平均值作為實驗結果。其中，N 為推薦列表中的商品總數，P 為目標用戶在前N 項中的商品數。

其中，精確度定義：

召回率定義：

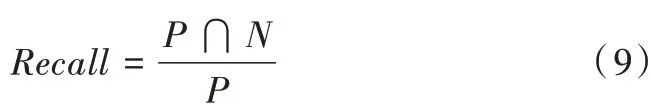
F1 定義：

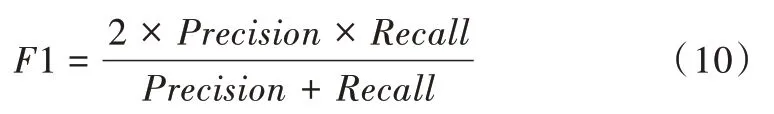
2.4 影響因素

影響算法結果的操作有3 個：①將兩種不同相似度計算方法（余弦相似度、改進余弦相似度）應用到基于商品的CF 算法中；②使用不同K 值（近鄰用戶數）比較兩種算法在不同K 值下的精確度和召回率；③使用不同Top N 算法的推薦長度，比較算法改進前后的精確度和F1-Score。考慮到加入時間衰減因子和懲罰因子后推薦商品的精確度，推薦列表不宜太長，因此本文將推薦列表長度設置為5、10、15、20。

2.5 實驗結果與分析

2.5.1 余弦相似度算法改進前后商品偏好得分變化

在相同參數下，根據用戶—商品評分矩陣計算相似度算法改進前后的商品偏好得分情況。以1196 號用戶為例，在返回40 個商品的條件下，運用改進的余弦相似度算法計算1196 號用戶對未評價商品的偏好分數為27.94，比傳統余弦相似度算法得出的商品偏好分數（65.87）下降了37.93，具體如圖1 所示。說明用戶對商品的偏好程度是隨著時間變化的，比較符合現實情況。

2.5.2 不同近鄰用戶數K 下算法的精確度和召回率

將改進相似度的算法稱為New Item CF，傳統的基于商品的CF 算法稱為Item CF。在K 值（近鄰用戶個數）不同，物品返回數為40 的條件下，兩種算法的精確度和召回率分別如圖2、圖3 所示。由圖2 可知，New Item CF 的精確度明顯高于Item CF，在K=200 時，New Item CF 的精確度達到最大，為0.18，比Item CF 的精確度提高了9%，二者差值也達到最大。由圖3 可知，在相同條件下，New Item CF 的召回率明顯高于Item CF，在K=200 時，New Item CF 的召回率達到最大，為0.17，比Item CF 提高了7.2%，二者差值也達到最大。

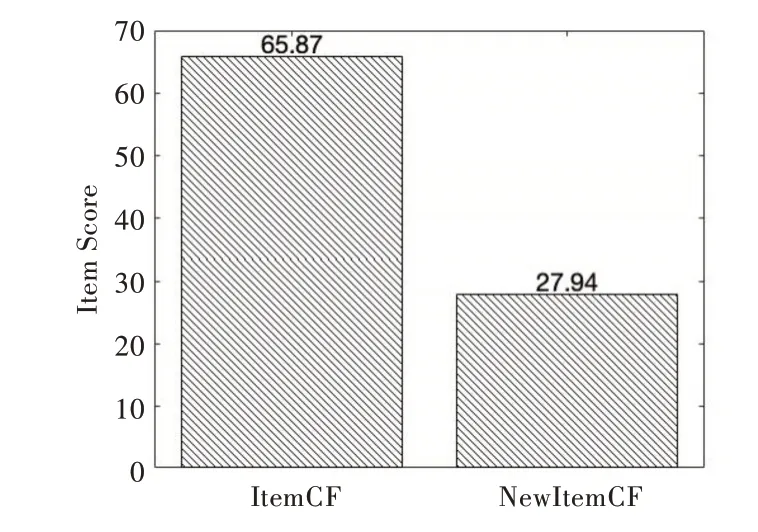
Fig.1 Score of items before and after similarity algorithm improvement圖1 相似度算法改進前后物品得分

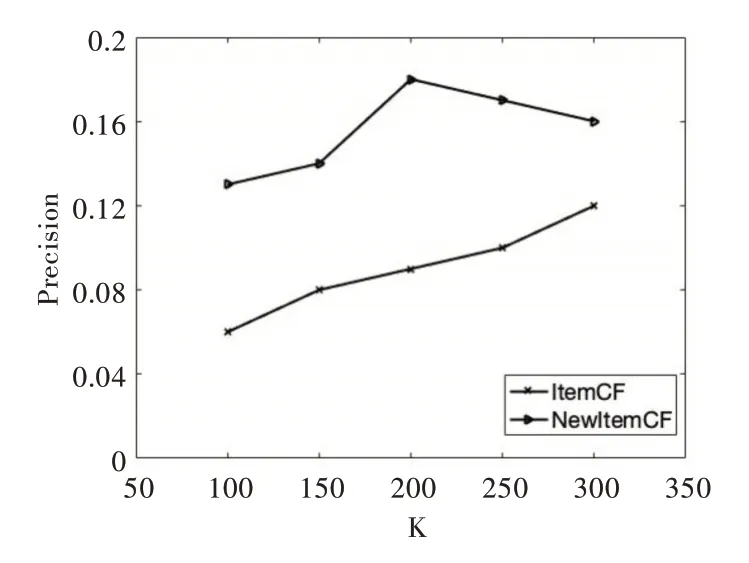
Fig.2 Precision comparison of recommendation results under different K values圖2 不同K 值下推薦結果的精確度比較

Fig.3 Changes of recall rate under different K values圖3 不同K 值下召回率的變化

2.5.3 不同Top N 算法下精確度比較

將商品近鄰數設置為40，通過設置不同推薦列表長度n 測試改進算法的精確度。由圖4 可知，當推薦長度為5時，New Item CF 算法的精確度大于Item CF 算法。然而，隨著推薦長度的增加，New Item CF 和Item CF 的精確度均開始下降，當Top N=10 時，Item CF 的精確度超過New Item CF。因此，在使用New Item CF 算法推薦商品時，推薦列表不宜過長。

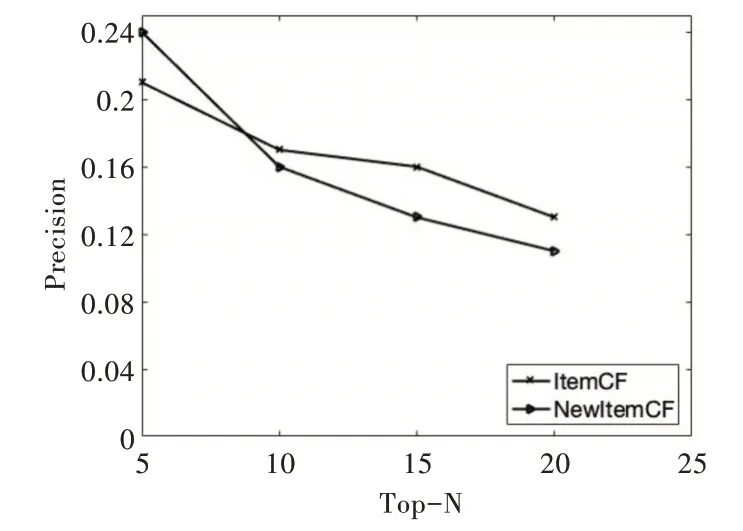
Fig.4 Precision under different Top-N algorithm圖4 不同Top-N 算法下的精確度

2.5.4 不同Top N 算法下F1 值比較

將商品近鄰數設置為40，通過設置不同推薦列表長度n 測試算法的F1 值。由圖5 可知，當推薦長度<15 時，New Item CF 的F1 值大于Item CF。但隨著推薦列表長度的增加，即當推薦長度>15 時，New Item CF 的F1 值小于Item CF。由此可知，加入時間衰減函數和物品懲罰因子后，隨著推薦長度的增加，New Item CF 的推薦效果會差于Item CF。

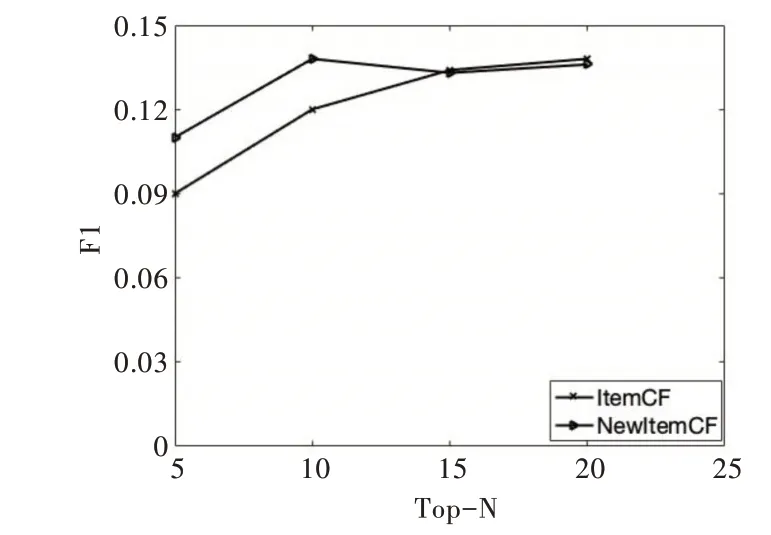
Fig.5 F1 values for different Top-N algorithm圖5 不同Top-N 算法下的F1 值

3 結語

在日常生活中，用戶的興趣愛好可能會隨著時間推移而發生變化。本文針對用戶的個性化需求將時間衰減函數和物品懲罰因子融入到相似度矩陣計算中，通過一系列數據證明，若實驗參數設置得當，在一定條件下，改進的推薦算法在精確度、召回率和F1 值方面比傳統CF 算法明顯提高，但當推薦列表長度不斷增加時，改進算法的精確度和F1 值開始下降，其性能開始弱于傳統CF 算法。下一步研究重點：①在不降低推薦精確度的同時擴大推薦商品的范圍，擴展用戶興趣面；②根據用戶心情變化快慢賦予具體參數，表示用戶當前不同的興趣特點，以更加精確和實時地進行個性化推送。