改進貝葉斯網絡的個性化隱私數據發布方法

陳思陽

（山東科技大學計算機科學與工程學院，山東青島 266590）

0 引言

在大數據時代，數據開放與共享已成為必然趨勢［1］。為了方便研究與應用，許多機構和組織會公開發布數據，然而這些數據可能包含個人敏感信息，如果直接發布會導致用戶隱私泄露。例如，疾病預防控制中心需要從各種醫療機構收集病例，若未經處理便發布了原始信息，患者個人信息可能會被非法利用，對其日常生活造成嚴重影響［2］。為解決該問題，諸多學者對隱私保護數據發布（Privacy-Preserving Data Publishing，PPDP）方法［3］進行了研究，目的是保護原始數據的隱私信息，同時為后續數據分析保留盡可能多的數據效用。

k-匿名模型［4］是PPDP 領域提出的第一個隱私保護模型，由于其簡單性和有效性而得到廣泛應用［5］。k-匿名模型雖然可以防止身份泄露，但不足以防御屬性泄露。因此，若干種擴展k-匿名模型被提出，如l-多樣性［6］、t-緊密度［7］、（k，l）-多樣性［8］、（α，ε）-匿名［9］、p-敏感度k-匿名［10］，以及各種改進的匿名模型［11-13］。這些模型大多是基于k-匿名模型的傳統隱私保護技術，需要特殊的背景攻擊假設，不能提供嚴格有效的數學證明，從而降低了隱私保護的可靠性。

差分隱私保護方法由Dwork［14］提出，其克服了傳統隱私保護方法的主要缺陷，無需考慮攻擊者擁有的背景知識，并使用嚴格的數學推理證明對隱私保護模型進行量化。該方法要求在查詢結果中添加噪聲，因此主要應用于查詢結果的發布中［15］。基于此，Hasan 等［16］提出一種非交互式保護框架，通過轉換或壓縮原始數據向查詢結果中添加噪聲以滿足ε-差分隱私。非交互式隱私保護模型可以發布經過離線處理且滿足差分隱私的數據集，用戶可以直接在數據集上執行查詢操作，解決了交互式場景下受到查詢接口限制的問題［17］。Zhang 等［18］提出的PrivBayes 是隱私保護數據發布方法的典型代表，該方法通過構建貝葉斯網絡保持屬性間概率的一致性，同時保留了原始數據的固有特征，后續許多學者在此基礎上進行了改進。例如，王良等［19］提出加權PrivBayes 方法，其考慮到字段屬性值的多樣性，優化選擇了屬性字段結點加入噪聲的順序，以構建更優的貝葉斯網絡；Li 等［20］提出平滑PrivBayes 方法，引入平滑敏感度機制，可以在實現差分隱私的同時減少噪聲，從而提高聯合分布的精度。

然而以上算法均未對實現差分隱私時屬性的敏感程度作出討論，因此本文提出一種改進貝葉斯網絡的個性化隱私數據發布算法CSAPrivBayes。該法通過關聯敏感屬性程度劃分屬性區域進而分配隱私預算，同時改進了貝葉斯網絡的初始結點隨機選擇機制，在保護隱私的同時保證了數據可用性。

1 差分隱私與貝葉斯網絡

1.1 差分隱私

差分隱私保護模型定義了極其嚴格的攻擊模型，成為數據發布領域最重要的隱私保護方法之一。

對于只有一個元組不同的兩個數據集D1和D2，如果隨機算法G滿足ε-差分隱私［14］，則對于隨機算法G，任何可能的輸出O滿足：

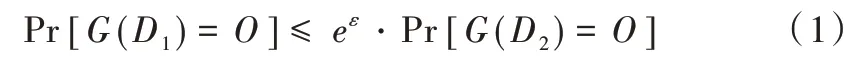
式中，Pr[?]為事件發生的概率，參數ε為隱私保護預算。F為將數據集映射到固定大小實數向量的函數。函數F的敏感度［21］定義為：

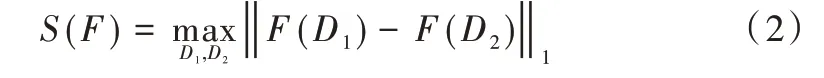
給定數據集D和查詢函數f:D→Rd，f的敏感度為S(f)。算法M(D)=f(D)+η通過向f(D)輸出的每個值添加隨機噪聲η來實現ε-差分隱私的Laplace 機制［21］。隨機噪聲η的概率密度函數為：

1.2 貝葉斯網絡

設A為數據集D上的一組屬性，Pr[A]為A上的聯合概率分布，屬性集A上的貝葉斯網絡描述了A中某些屬性之間的條件獨立性。貝葉斯網絡為有向無環圖，其將A中的每個屬性表示為一個結點，使用有向邊對A中屬性之間的條件獨立性進行建模。圖1 展示了具有5 個屬性的集合A上的貝葉斯網絡。

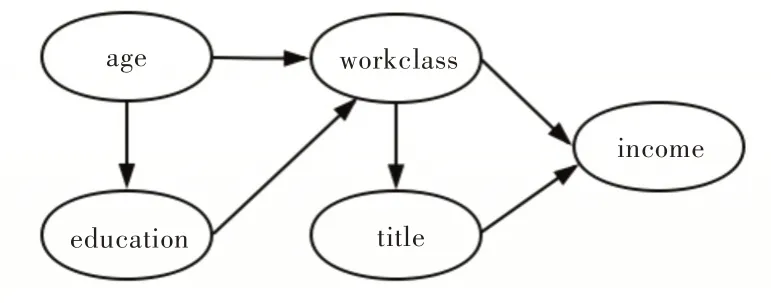
Fig.1 Bayesian network圖1 貝葉斯網絡

Pr[A]表示數據集D的全分布，貝葉斯網絡實質上是用d 個條件分布Pr[X1|Π1],Pr[X2|Π2],…,Pr[Xd|Πd]以近似全分布Pr[A]。在給定Xi的屬性父結點集Πi的情況下，任意Xi和Xj?Πi是條件獨立的，可得到：

2 基于貝葉斯網絡的個性化差分隱私算法

2.1 PrivBayes 算法

PrivBayes 是一種用于發布高維數據的差分隱私方法，主要包括以下3 個步驟，分別為構建貝葉斯網絡、擾動概率分布和隨機取樣［18］。

（1）在構建貝葉斯網絡階段，從屬性集合中隨機選擇一個屬性作為貝葉斯網絡的起點，采用貪心算法從剩余屬性中選擇出具有最大互信息的父子結點對，并將其添加到貝葉斯網絡中。當所有結點被添加到貝葉斯網絡中后，輸出構造完成的貝葉斯網絡。

（2）在擾動概率分布階段，首先根據構建的貝葉斯網絡計算屬性的聯合概率分布P[Xi,Πi]，然后將拉普拉斯噪聲注入P[Xi,Πi] 以獲得 噪聲分 布P*[Xi,Πi]。添加到P[Xi,Πi]的拉普拉斯噪聲比例設定為4(d-k)/nε，確保P*[Xi,Πi]的生成滿足(ε/2(d-k))-差分隱私，P[Xi,Πi]具有的敏感度。

（3）在隨機取樣階段，首先將第一個屬性結點按照屬性取值劃分概率區間，生成一個隨機數，根據其所在的取值區間確定X1的取樣值。對于剩余屬性結點，在給定父結點下按照屬性取值劃分聯合概率區間，再根據生成隨機數所在概率區間確定X的取樣值。

2.2 CSAPrivBayes 算法

PrivBayes 算法解決了高維數據的發布安全問題，但也存在一些不足。該算法隨機選取了首個屬性，通過向屬性的低維聯合分布概率加入拉普拉斯機制實現差分隱私保護，并沒有考慮敏感屬性和一般屬性，可能導致敏感屬性隱私泄露以及一般屬性隱私保護過度。為此，本文提出CSAPrivBayes 算法，首先定義靜態權重值作為選取首個網絡結點的依據以提高貝葉斯網絡精度，再根據準標識符屬性關聯敏感屬性的程度進行區域劃分，進而采用不同隱私預算，實現個性化差分隱私保護。算法具體步驟如下：

（1）輸入：數據集D、參數k、閾值θ。

（2）輸出：低維帶噪數據集D'。

（3）對數據集D進行預處理，采用二分k均值算法將連續屬性離散化。

（4）計算數據集D中所有屬性X的靜態權重值W，選取W值最大的屬性作為X1，將其添加到網絡N中。對于有d個屬性的數據集，屬性Xi的靜態權重值為：

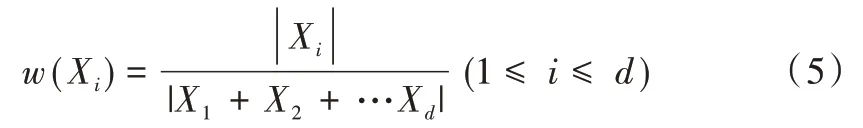
（5）使用貪婪搜索策略選擇最大的互信息對(Xi,Πi)，將其添加到貝葉斯網絡N中。

（6）重復步驟（5）直至選擇出(d-1)個AP對。

（7）計算N中屬性結點Xi的聯合概率分布P[Xi,Πi]。

（8）計算N中所有屬性與敏感屬性的互信息I(Xi,S)。數據集D中的準標識符屬性Qi與敏感屬性S的互信息為：

（9）如果屬性Xi的I(Xi,S)≥閾值θ，則將其劃分到區域A，否則劃分到區域B。

（12）將加噪的聯合分布P*[Xi,Πi]中的負值歸零并歸一化。

（13）從P*[Xi,Πi]中隨機采樣P*[Xi|Πi]生成低維帶噪數據集D'。

（14）輸出低維帶噪數據集D'。

3 實驗與結果分析

3.1 實驗環境與數據集

硬件環境：Intel（R）Core（TM）i5-5200U CPU@ 2.20 GHz，內存8G，操作系統Win7_64 位旗艦版；軟件環境：使用Python 編程語言實現，IDE 開發工具為Pycharm。使用美國人口普查數據集，隨機選擇24 000 條數據，其中選取6 個離散屬性，4 個連續屬性，具體信息如表1 所示。

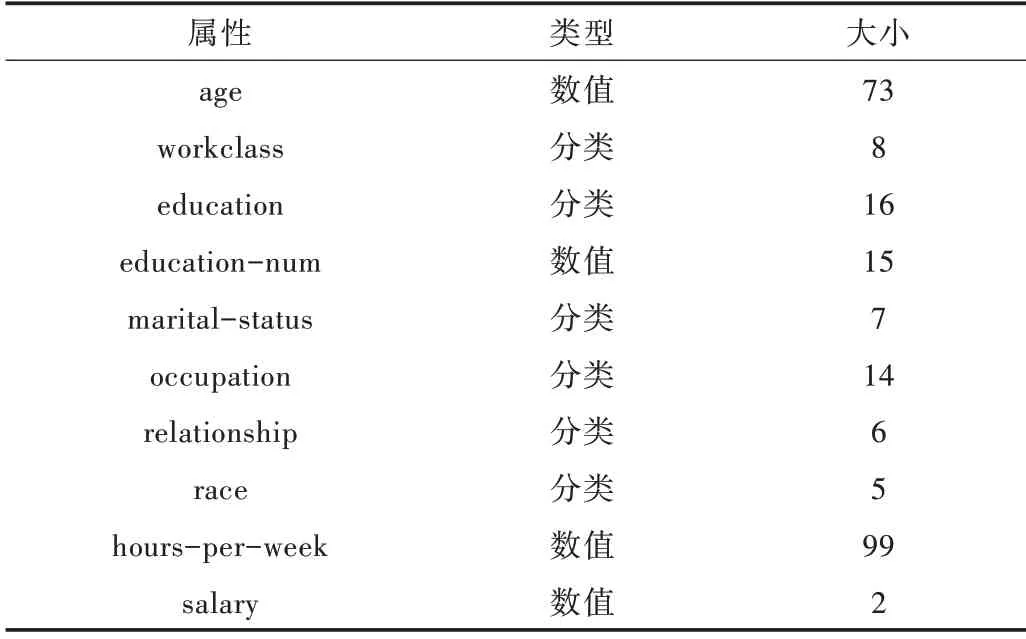
Table 1 Dataset information表1 數據集信息

3.2 評價指標

使用誤分類率評估所發布合成數據集的可用性，誤分類率越小，數據集的可用性越高。設FN為實際為正例且被分類器分為負例的個數，FP為實際為負例且被分類器分為正例的個數，P為實際的正例個數，N為實際的負例個數，則誤分類率的計算公式為：

使用分類準確率評估所生成貝葉斯網絡分類的精確度，分類準確率越高，貝葉斯網絡的精確度越好。設TP為實際為正例且被分類器分為正例的個數，TN為實際為負例且被分類器分為負例的個數，則分類準確率的計算公式為：

3.3 實驗結果分析

使用SVM 算法評估發布數據的可用性，分類變量為salary 屬性，將Adult 數據集的80%作為訓練集，20%作為測試集。實驗采用交叉驗證比較PrivBayes 與CSAPrivBayes算法的平均誤分類率，結果如圖2 所示。

由圖2 可以看出，隨著隱私預算的增加，加入的噪聲變小，數據的可用性變好，兩種算法的誤分類率均呈下降趨勢。然而，CSAPrivBayes 算法考慮了屬性敏感程度，合理分配隱私預算，誤分類率降至15%，遠低于PrivBayes 算法，在數據可用性方面也表現更佳。

采用分類準確率評估PrivBayes 與CSAPrivBayes 算法的貝葉斯網絡質量，取k值為3，ε值為1.6，跟隨數據量的變化比較兩種算法的表現。如圖3 所示，通過PrivBayes 和CSAPrivBayes 兩種算法構建了不同的貝葉斯網絡結構，隨著訓練數據量的增加，兩種貝葉斯網絡的分類準確率均逐步提高。CSAPrivBayes 算法根據屬性結點的重要程度確定首選結點，分類準確率達到84%，構建的貝葉斯網絡質量優于PrivBayes 算法。

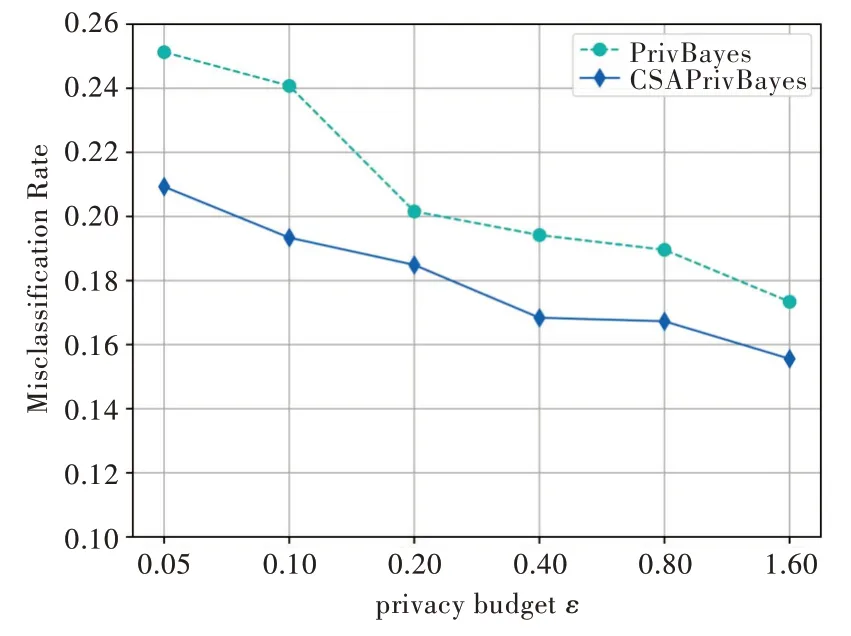
Fig.2 Comparison of attribute misclassification rate of the two algorithms on Adult dataset圖2 Adult 數據集上兩種算法的錯誤分類率比較

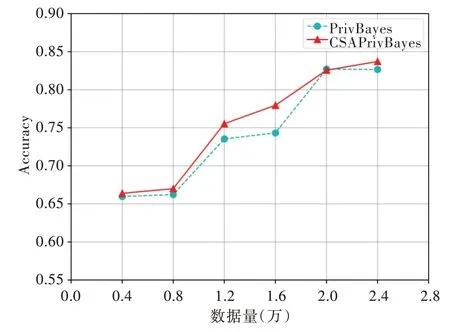
Fig.3 Accuracy comparison of the two algorithms on Adult dataset with ε=1.6圖3 ε=1.6 時兩種算法在Adult 數據集上的準確率比較

4 結語

為解決PrivBayes 算法隨機選擇首選結點與無法合理分配隱私預算的問題，本文提出一種改進的隱私數據發布方法CSAPrivBayes。其通過對屬性結點添加權重值確定首選機制，根據關聯敏感屬性程度分配隱私預算實現個性化隱私保護。實驗結果表明，CSAPrivBayes 算法可以提高所構建貝葉斯網絡的精度以及合成數據的可用性。在后續研究中，可通過使用不同的啟發式算法構建貝葉斯網絡，進一步優化CSAPrivBayes 算法的性能。