基于Kriging插值和BP神經(jīng)網(wǎng)絡結(jié)合的糧倉溫度場預測模型研究及實現(xiàn)

王傳旭, 王康, 陳林, 李學, 張紅偉

(安徽大學電子信息工程學院, 計算智能與信號處理教育部重點實驗室， 合肥 230039)

我國糧食年產(chǎn)量增長迅速，但是糧食儲藏過程中的損耗也不容忽視，對糧倉內(nèi)糧堆溫度的準確把握是保證儲糧安全的前提。一旦糧堆發(fā)生小部分發(fā)熱現(xiàn)象，若不及時處理就會造成糧倉內(nèi)部濕熱環(huán)境劇烈變化、糧堆出現(xiàn)結(jié)露、演化成霉變，從而對儲備的糧食造成重大損失[1]。因此，準確掌握糧堆溫度分布、合理分析預測糧堆溫度變化趨勢是保障儲糧安全狀態(tài)的重要措施。為了合理預測糧溫信息，學者們基于數(shù)值分析進行溫度場建模，如Gastón等[2]依據(jù)糧食水分等溫吸附方程和熱質(zhì)局部平衡原理，視糧堆為多孔介質(zhì)，建立了糧堆熱濕耦合模型；尹君等[3-5]對糧堆進行多場耦合并建立了仿真圖像分析模型，成功復現(xiàn)糧堆在冬末春初和夏季的溫度場分布狀況，準確預測了糧堆可能結(jié)露的位置。基于數(shù)值分析建立的溫度場模型雖然較為精確，但需要專門的軟件進行數(shù)值模擬來建立數(shù)學模型，計算量大，難以滿足工程應用需求，因此，基于糧情大數(shù)據(jù)進行數(shù)據(jù)分析的方式被逐漸應用于糧堆溫度的預測[6-7]。沈兵[8]利用BP神經(jīng)網(wǎng)絡來預測儲糧安全。Duan等[9]通過分析糧堆的大量歷史數(shù)據(jù)與相應天氣預報數(shù)據(jù)之間的相關性，采用支持向量回歸方法基于天氣數(shù)據(jù)來預測谷物堆的平均溫度。

對比于溫度場建模方法，數(shù)據(jù)分析能夠較為簡易地對單點溫度或平均溫度進行預測，但對于復雜的倉儲環(huán)境，預測結(jié)果不足以表現(xiàn)出整個糧倉內(nèi)部溫度的變化趨勢，很難預測到倉中出現(xiàn)局部溫度異常的情況，導致理論預測與實際情況偏差較大。為此，本文擬結(jié)合上述兩種方法的優(yōu)勢，采用糧倉內(nèi)已有監(jiān)測點的溫度及空時數(shù)據(jù)進行溫度場預測，設計溫度場預測模型。通過該模型對倉內(nèi)多個監(jiān)測點測溫數(shù)據(jù)進行時序上的預測，得到倉內(nèi)離散的溫度預測值，再利用預測出的溫度值進行空間上的插值估計建立倉內(nèi)的預測溫度場，以期為各種倉儲過程中糧食溫度預測提供基礎，確保糧食安全。

1 材料與方法

1.1 空時溫度場模型

本文利用分布式糧倉測控系統(tǒng)中各監(jiān)測點的歷史數(shù)據(jù)對糧倉內(nèi)溫度進行空時分析。首先對糧倉進行空間重建，將每個溫度點的數(shù)據(jù)對應到糧倉的各個位置，以現(xiàn)場的電纜排布為標準，以a、b、c代表糧倉的行、列、層，對溫度數(shù)據(jù)進行時序上預測，然后再進行空間上的插值估計。模型公式如式(1)所示。

(1)

式中，Zt+1(ε)為糧倉空間插值點的預估溫度 ，ε為空間的不同位置；Zt+1(εi)為已知位置，即傳感器所在位置的預測溫度值，εi為傳感器位置，以行列層信息(a,b,c)確定；λi為溫度場的數(shù)值計算中已知位置的權重系數(shù)；Zt-j(εi+d)為糧倉中不同位置傳感器的歷史時間點數(shù)據(jù)，D為近鄰傳感器的個數(shù)，J為歷史數(shù)據(jù)的時間長度；φjd為溫度點預測中不同位置不同時刻對應的權重系數(shù)，f(x)代表一種非線性組合。

本文將BP神經(jīng)網(wǎng)絡和地質(zhì)學中的Kringing插值方法[10-11]相結(jié)合，實現(xiàn)式(1)的溫度場預測模型，采用BP神經(jīng)網(wǎng)絡對離散的溫度點進行數(shù)據(jù)分析，完成模型中溫度值預測的功能，再使用Kringing插值法將糧倉空間劃分成細小的區(qū)塊進行插值，建立溫度場。

1.2 模型實現(xiàn)

1.2.1BP神經(jīng)網(wǎng)絡 BP神經(jīng)網(wǎng)絡是一種適于非線性模式識別和分類預測的人工神經(jīng)網(wǎng)絡[12-13]，由輸入層、隱含層和輸出層組成。

輸入層的輸入序列為糧堆的溫度數(shù)據(jù)以及濕度數(shù)據(jù)。從數(shù)據(jù)庫取出的數(shù)據(jù)需要預處理，再作為神經(jīng)網(wǎng)絡的輸入序列。首先將溫度點對應到糧倉的各個位置，以現(xiàn)場的電纜排布為標準進行數(shù)據(jù)排列，令X(a,b,c)為第a行、b列、c層的溫度點數(shù)據(jù)序列。

X(a,b,c)=[x1(a,b,c),x2(a,b,c),…,xt(a,b,c)]

(2)

式中，X(a,b,c)代表第a行、b列、c層的溫度點數(shù)據(jù)，t為當前溫度點溫度數(shù)據(jù)的個數(shù)。

將溫度數(shù)據(jù)處理好后，結(jié)合濕度數(shù)據(jù)，進行BP神經(jīng)網(wǎng)絡的訓練。BP神經(jīng)網(wǎng)絡的框架如圖1所示。

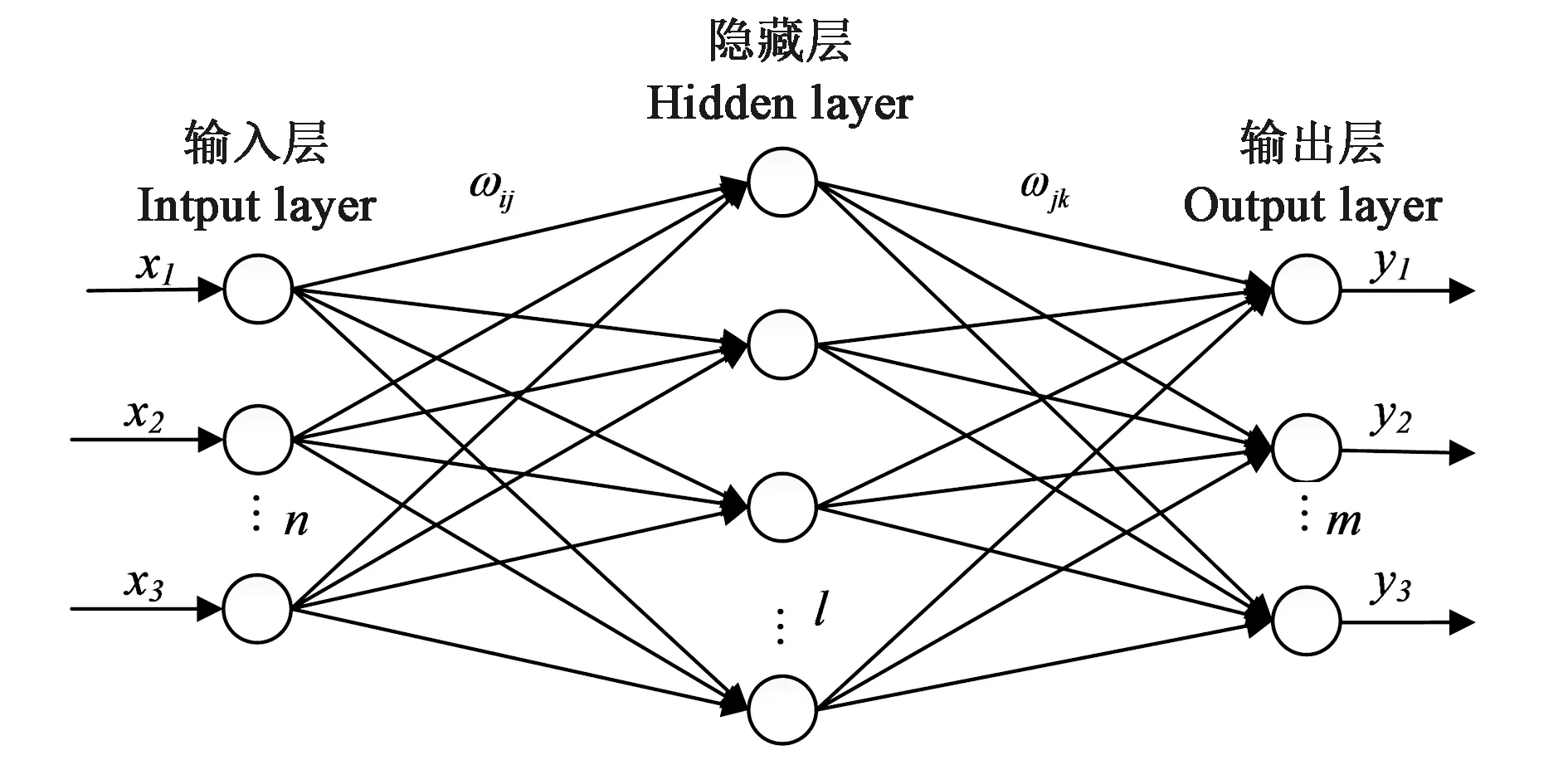
圖1 BP神經(jīng)網(wǎng)絡Fig.1 BP neural network

BP神經(jīng)網(wǎng)絡算法有兩部分：一是信號由輸入到輸出的正向傳播，二是神經(jīng)網(wǎng)絡輸出值與期望值的誤差從輸出到輸入的逆向調(diào)節(jié)。在正向傳播過程中，輸入信號從輸入層輸入，經(jīng)過隱含層，到達輸出層產(chǎn)生輸出信號。在輸出層，比較輸出值和期望值，如果其差值不滿足設定條件，那么這個誤差就需要逆向傳播去調(diào)節(jié)權值閾值。在逆向調(diào)節(jié)階段，誤差由輸出端開始逐層向前傳播，對隱含層到輸出層的權值和閾值、輸入層到隱含層的權值和閾值進行調(diào)節(jié)。神經(jīng)網(wǎng)絡的訓練具體步驟如下所示。

①信號正向傳播。

假設輸入層、隱含層、輸出層的節(jié)點個數(shù)分別為n、l、m，隱含層的輸出Hj如式(3)所示。

(3)

式中，xi為經(jīng)過預處理之后的溫度序列，ωij為輸入層到隱含層的權重，αj為輸入層到隱含層的偏置，g(x)為激勵函數(shù)。

輸出層的輸出Ok如式(4)所示。

(4)

式中，ωjk為隱含層到輸出層的權重;βk為隱含層到輸出層的偏置；ξ為1～10的常數(shù)。

誤差公式E如式(5)所示。

(5)

式中，yk為期望輸出，ok為神經(jīng)網(wǎng)絡輸出。

②誤差反向傳播。

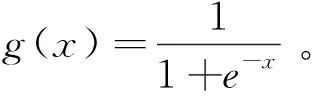
令ek=yk-ok。隱含層到輸出層的權值的迭代更新、輸入層到隱含層的權值迭代更新方法如式(6)所示。

(6)

隱含層到輸出層的偏置迭代更新和輸入層到隱含層的偏置迭代更新方法如式(7)所示。

(7)

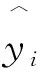
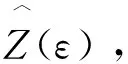
(8)

式中，Z(εi)為倉內(nèi)實際溫度傳感器第i個位置處的溫度預測值；ε是預測位置；w測量值數(shù)；λi為權重系數(shù)，λi的取值直接決定了待估計值的精度，由于Kriging插值的依據(jù)是無偏最優(yōu)估計，則λi應滿足以下條件。

(9)

1.3 模型實現(xiàn)

取數(shù)據(jù)庫中一個倉庫的定時數(shù)據(jù)作為樣本數(shù)據(jù)，對監(jiān)測點先進行預處理，結(jié)合空間信息得到每個溫度點對應的位置，重新排列數(shù)據(jù)作為BP神經(jīng)網(wǎng)絡中訓練集和測試集，得到訓練好的神經(jīng)網(wǎng)絡以及預測的溫度值，進行Kriging插值，結(jié)合倉庫實際信息，得到真實倉房內(nèi)的溫度場預測圖。具體實現(xiàn)流程如圖2所示。

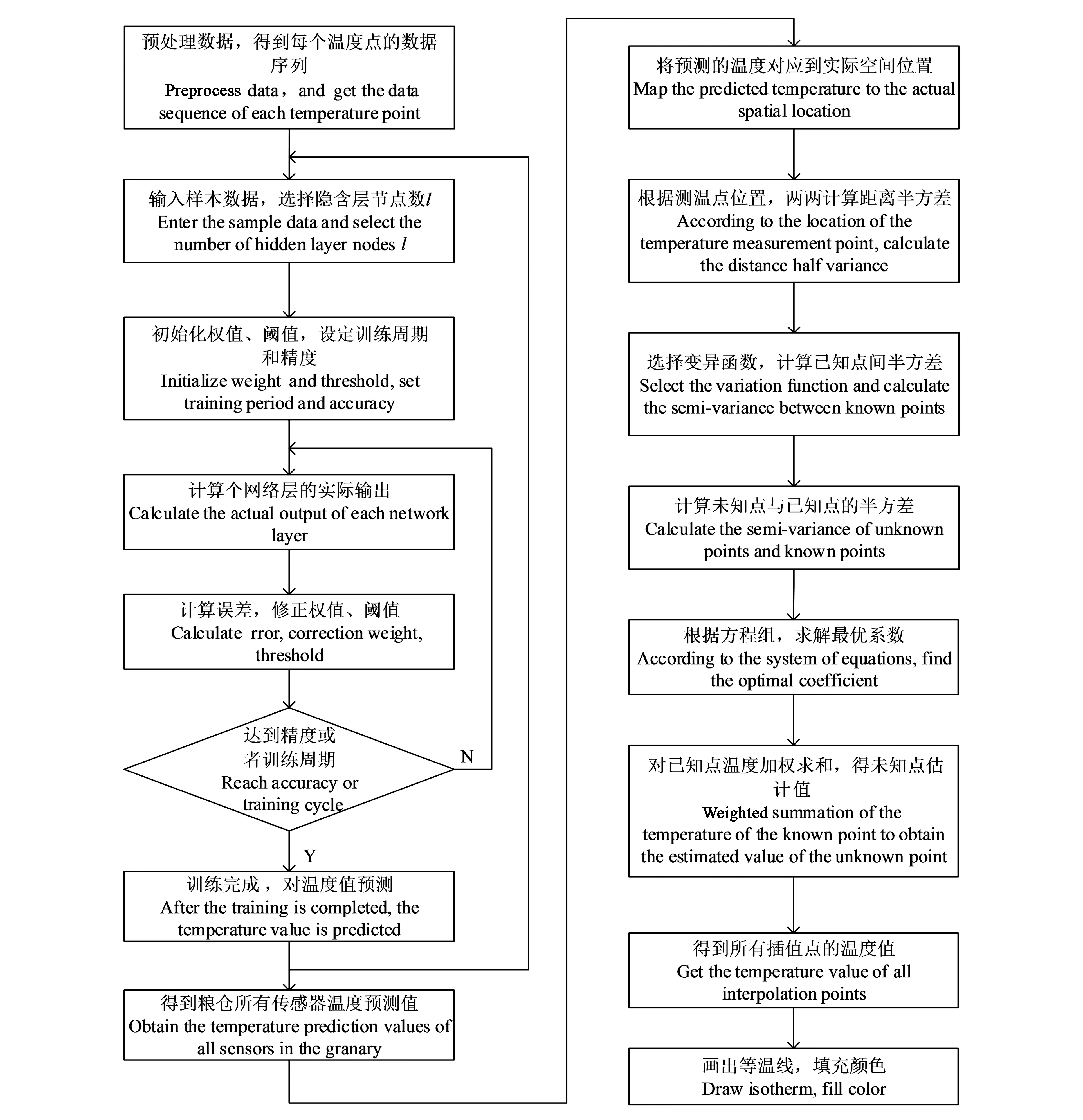
圖2 基于BP神經(jīng)網(wǎng)絡的糧倉空時溫度場預測流程Fig.2 Prediction flow of space-time temperature field of granary based on BP neural network

1.4 精度檢驗

本文以均方根誤差(RMSE)和平均絕對百分誤差(MAPE)來檢驗模型精確度，如公式(10)和(11)所示。

(10)

(11)

式中，N為樣本個數(shù)，x(εi)為實際溫度值，Z(εi)為溫度場預測圖中對應位置的預測值。

1.5 平臺搭建

在糧情數(shù)據(jù)庫中取某個糧情用戶下的一個倉進行溫度場預測，數(shù)據(jù)范圍為最近一年的定時數(shù)據(jù)，去除無效數(shù)據(jù)后，共計720條數(shù)據(jù)。BP 神經(jīng)網(wǎng)絡設定最大訓練次數(shù)為5 000次，學習率為0.05，訓練要求精度為10-3。訓練集與測試集比例為19∶1。Kriging插值半變異函數(shù)選取球形函數(shù)。該倉庫為7行6列4層。

2 結(jié)果與分析

2.1 溫度點預測結(jié)果分析

根據(jù)各個溫度點位置尋找近鄰點，取當前溫度點相鄰的溫度點作為近鄰點。如第一行第一列第二層的溫度點(1,1,2)，其近鄰點一共有四個(1,1,1)(1,1,3)(2,1,2)(1,2,1)。這說明該溫度點位于糧倉長方體空間的外層棱地方，屬于外層溫度點，受外溫外濕的影響較大，所以在訓練時，其神經(jīng)網(wǎng)絡輸入序列包括幾個溫度點的數(shù)據(jù)以及大氣數(shù)據(jù)。再如溫度點(4,3,2)，其近鄰點一共有六個(4,3,1)(4,3,3)(4,2,2)(4,4,2)(3,3,2)(5,3,2)。這說明該溫度點位于糧倉長方體空間的內(nèi)部，屬于“內(nèi)芯”溫度點，受倉外溫度和濕度的影響較小，其溫度波動除自身變化外還與周圍空間糧食的熱量傳輸相關，所以在訓練時，其神經(jīng)網(wǎng)絡輸入序列只包括幾個溫度點的數(shù)據(jù)即可。

運用BP 神經(jīng)網(wǎng)絡方法對數(shù)據(jù)進行分析處理，設定訓練周期以及精度，對訓練集進行訓練，用測試集進行測試，取糧倉中某個點的訓練結(jié)果進行展示，結(jié)果如圖3所示，從倉內(nèi)某點的溫度預測對比圖可以看出，測試集測試結(jié)果良好，預測的溫度變化趨勢與實際一致，誤差很小。

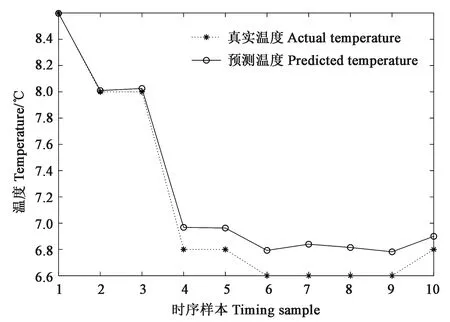
圖3 坐標(1,1,1)的溫度預測對比Fig.3 Comparison of temperature predictions at coordinates (1,1,1)

選取相應平面的歷史數(shù)據(jù)經(jīng)過BP神經(jīng)網(wǎng)絡預測后，得出平面中不同位置的溫度點預測值，得到其平均絕對百分誤差為1.253 5%，均方根誤差為0.106 0。

從表1可以看出，整個平面各監(jiān)測點的溫度預測效果也是良好的。

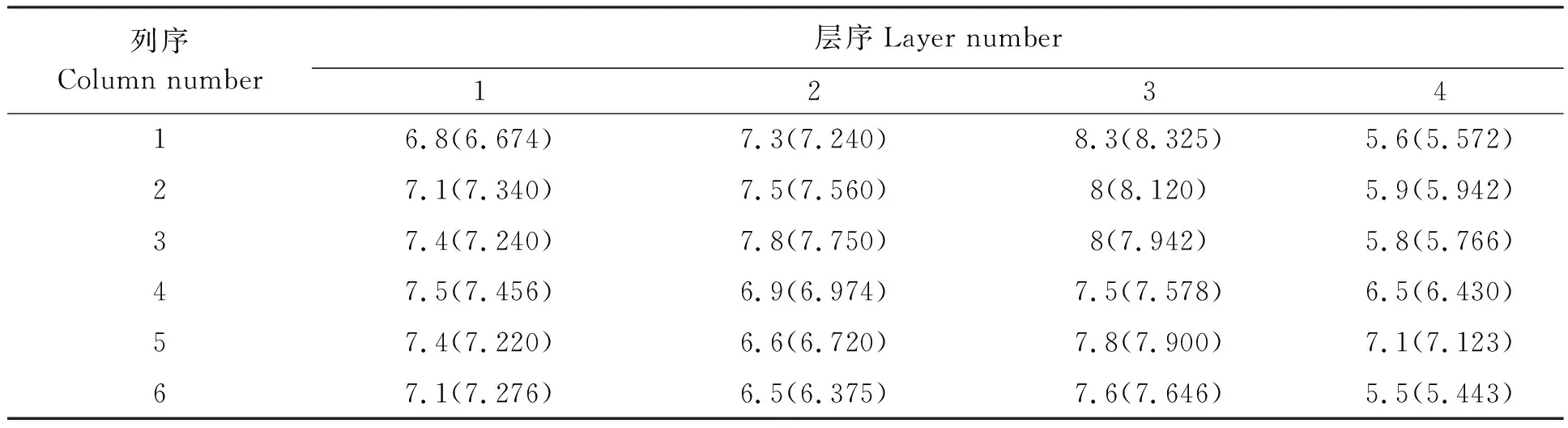
表1 第一行電纜各監(jiān)測點實際溫度與預測溫度的對比Table 1 Comparison of actual temperature and predicted temperature of each monitoring point of the first row of cables (℃)

2.2 溫度場預測結(jié)果分析

2.2.1溫度場云圖分析 在得出當前平面的溫度預測值后，結(jié)合實際的倉庫信息，將溫度點的空間分布還原到實際場景中，并根據(jù)溫度點的預測值進行Kriging插值，得出該平面的溫度場分布。本倉庫長40 m，寬35 m。行列之間的間距為5 m，最外層電纜距四周墻壁距離為2.5 m；層間間距為1.5 m，最頂層測溫點距頂層間距為0.75 m。測溫點自上而下排布，截面上的坐標(1,1)對應的就是實際倉庫截面圖中的(0.75,5.25)，以此類推進行繪圖，圖4為實際溫度場和預測溫度場對比，可以看出，不同層面的溫度基本一致，表明預測結(jié)果準確度高。

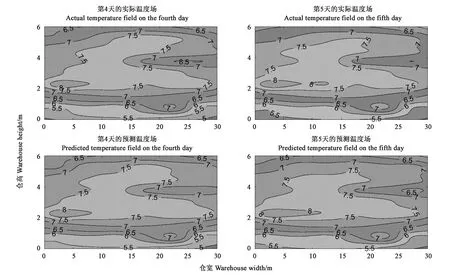
圖4 實際溫度場和預測溫度場對比Fig.4 Comparison between actual temperature field and predicted temperature field

2.2.2溫度場預測精度分析 由于預測出的溫度場和預測出的點屬不同維度，采用極限逼近方法進行比較，即留M法，留出M個已知點的位置做空白處，用剩下的(N-M)個已知點溫度去估計M個未知點，最后逼近單點估計的效果，由平均絕對百分誤差和均方根誤差衡量，實驗結(jié)果如表2所示。

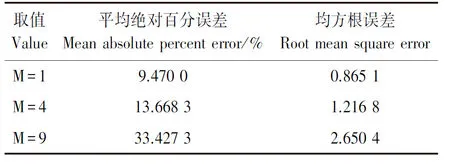
表2 “留M法”驗證效果對比Table 2 Comparison of the effect of verification by “retain M method”

從表2可以看出， M值越大，平均絕對百分誤差和均方根誤差越大，對未知點估計的準確度就越低。M值越大代表已知點的數(shù)目越小，已知點的數(shù)目越小，預估效果越差，當已知點為1時，其預估效果必定比(N-1)個已知點條件下的預估效果差。因此，本模型的溫度場預測方式比單點溫度預測方式效果更好。

3 討論

在科學儲糧背景下，儲藏過程中糧食溫度預測研究尤為重要。目前，多數(shù)學者以數(shù)值分析方式結(jié)合熱力學、流體力學等專業(yè)學科知識進行溫度場建模，能夠利用模型精確反映糧堆的溫度分布以及變化規(guī)律，但是其建模過程過于專業(yè)化，難以達到實際工程的需求。對比于溫度場建模分析方法，數(shù)據(jù)分析是挖掘已有的糧堆監(jiān)測數(shù)據(jù)自身所體現(xiàn)的規(guī)律，對糧堆單個測量點溫度或者均溫進行預測，實現(xiàn)過程較為簡易，但是這種預測單點溫度或均溫的方式無法反映糧倉內(nèi)的溫度分布詳情，無法掌握糧堆各處的的溫度變化。

本研究基于數(shù)據(jù)分析預測溫度，并采用地質(zhì)學中的Kriging插值法對糧倉內(nèi)部空間進行溫度插值，建立溫度場。該方法相較于傳統(tǒng)的數(shù)值分析建模方式更加簡易可行，實現(xiàn)復雜度低，易通過編程語言實現(xiàn)，相應的功能模塊能獨立實現(xiàn)，可嵌入到實際的糧情測控系統(tǒng)，使預測更為便捷。相較于單點溫度或均溫的預測方式，能夠展現(xiàn)出糧倉溫度變化的整體趨勢，更為細致地反映出糧倉糧堆內(nèi)部溫度信息，為可疑點的扦樣準確度提供了理論依據(jù)。