面對未知坡面的四足機器人足端軌跡仿真研究

宮赤坤，刁海參，賀飛翔

（200082 上海市 上海理工大學 機械工程學院）

0 引言

在近年來的研究中，國內外許多研究院已進行了一系列的研究工作。山東大學高效潔凈機械制造教育部重點實驗室提出了一種通過質心調整法來減少四足機器人坡面上的足地接觸的沖擊力。張培強[1]設計了一種腿長可變的四足機器人模型，通過增大后腿小腿長度的同時減小前腿腿長的方法調整機身質心，以此來使四足機器人在坡面上穩定運動；孔垂麟設計了一種基于控制足端運動軌跡讓機器人實現在斜面上平穩運動的方案，并進行了穩定裕度分析，綜合機器人的運動連續性考慮，給出了一個通過控制身體俯仰角來實現斜面連續平穩運動的方法。如圖1，本文設計了一種液壓驅動的12 自由度四足機器人，通過參考俯仰角的變化量來調整機器人坡面的質心位置，并根據俯仰角的變化量對足端軌跡進行實時重新解算，使得足端力豎直于地面而非坡面，為增加四足坡面穩定性提供支撐。使四足機器人實現30°坡面的穩定運動。

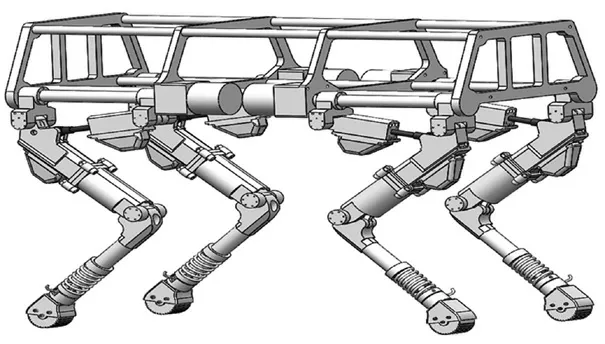
圖1 四足機器人模型Fig.1 Quadruped robot model

1 四足機器人機械結構設計

綜合考慮四足機器人運動的穩定性和機動性，本文設計了一種12 自由度的四足機器人[2]。該四足機器人由機身和4 條腿構成，每條腿有3個旋轉自由度，分別是前擺髖關節、側擺髖關節和膝關節。在對角小跑步態下，對角線上的兩條腿可同時抬起、下降、擺動或支撐，單腿在擺動相與支撐相之間交替轉換。在進行大角度爬坡時，單腿液壓缸行程能始終控制在有效行程內。

2 四足機器人仿真流程

本文采用ADAMS與MATLAB進行聯合仿真。仿真分為3 個步驟：首先在三維軟件中構建四足機器人的模型，并將所建立的模型導入ADAMS中，初步建立好仿真的機械系統模型；然后由ADAMS 系統給出三維虛擬樣機模型、運動學模型和動力學模型；最后在Simulink 平臺中建立步態控制系統，由Simulink 提供實時的關節驅動數據，使得ADAMS 與MATLAB-Simulink 進行數據交互，實現聯合仿真。參見圖2。

3 足端軌跡規劃及質心調整原理

以Walk 步態為例，分別進行左前腿與右后腿、右前腿與左后腿規律性的擺動，根據四足足端軌跡的時序，結合五次多項式進行設計[3]，點狀圖如圖3 所示。

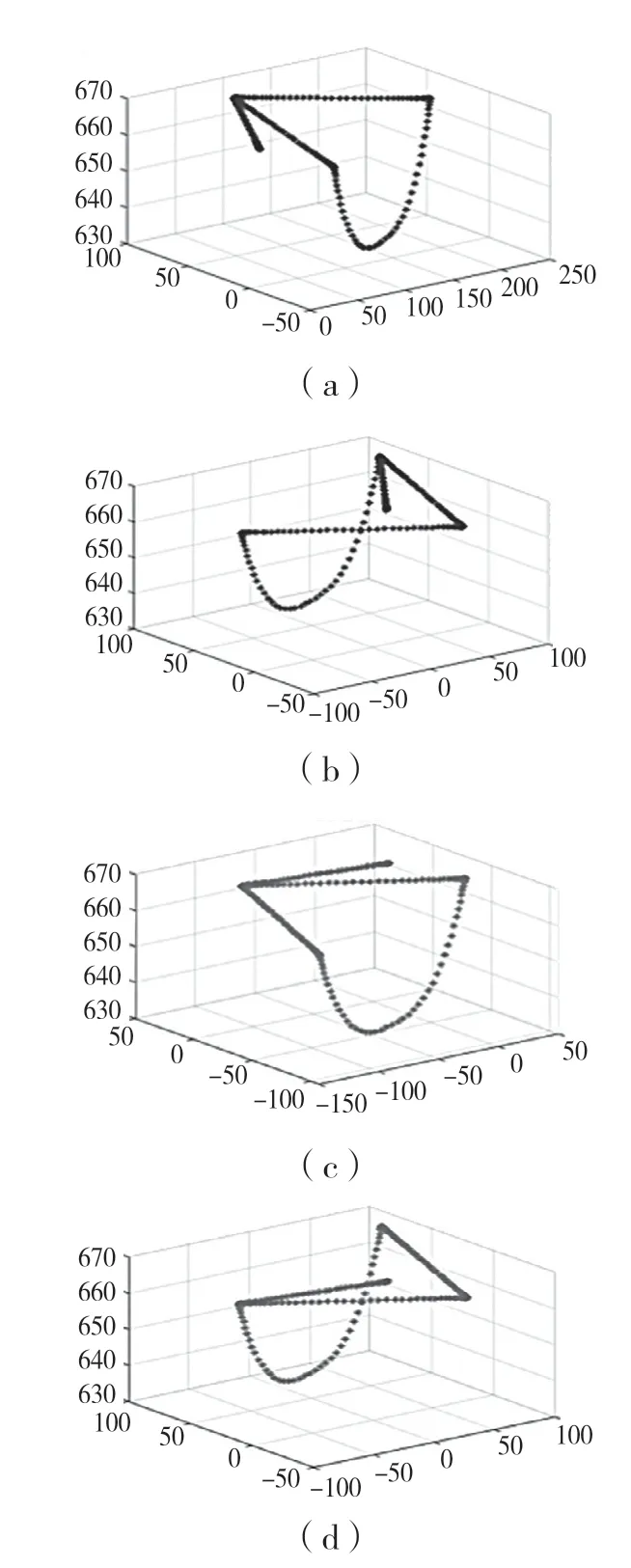
圖3 足端運動軌跡Fig.3 Foot trajectory

四足機器人的左側腿擺動時形成的右側支撐域，該過程中前右腿 FR 和后右腿 HR 均處于支撐狀態。當后左腿 HL 擺動時，前左腿 FL 與右側兩支撐腿構成支撐三角形；當前左腿 FL 擺動時，后左腿 HL 與右側兩支撐腿構成支撐三角形，兩個支撐三角形構成公有支撐三角形。為了降低四足機器人運動時摔倒的風險，ZMP 應該落在支撐域的內部[4-5]。參見圖4。

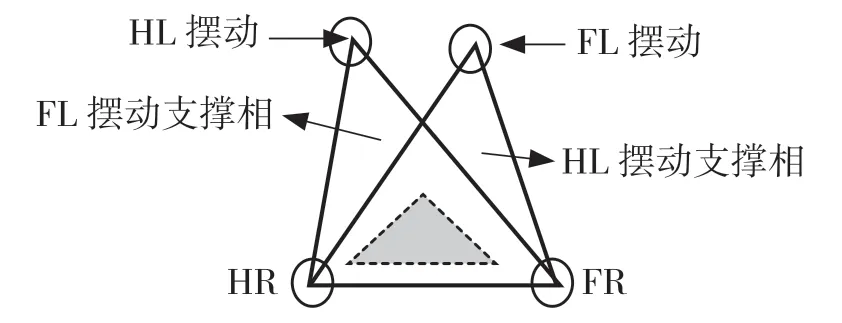
圖4 質心投影圖Fig.4 Centroid projection

由圖5 可見，質心由B 變化到B'，記質心到后腿足端的連線繞后腿足端轉過的角度為β，則

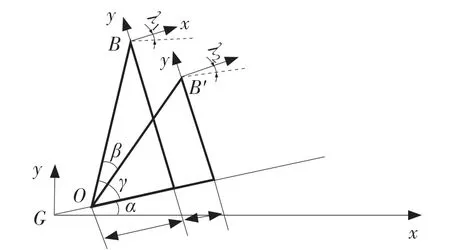
圖5 質心調整圖Fig.5 Centroid adjustment chart

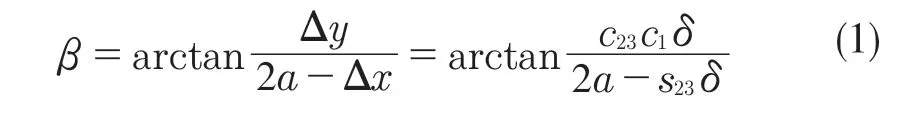
由于機器人整體繞后腿足端旋轉β角，可以求得在水平面坐標系G 下質心的位移量和機體坐標系轉過的角度分別為

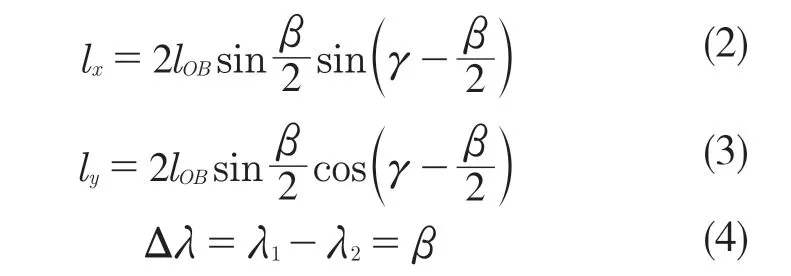
需要將機器人質心向前移動距離S，才能使其與支撐對角線交點重合，即

對比之前的步態規劃，可對足端軌跡做如下調整[6]：

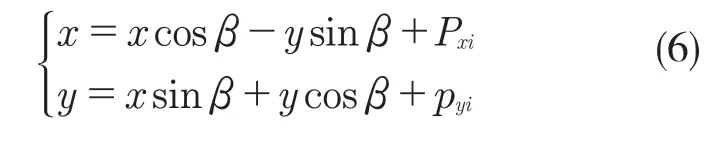
4 運動學建模與控制平臺搭建

本文采用的是12 自由度內膝肘式仿生四足機器人，相較于其他四足機器人結構，內膝肘式四足機器人運行較為穩定[7]。為了簡化仿真內容，模型設立為每條腿3 個自由度，分別在側擺關節、大腿關節和小腿關節。在SolidWorks 中建立起四足機器人的三維模型后，存為BIN 格式文件導入ADAMS 中，并設置模型的材質、密度、質心等物理參數。

模型建立完成后，設置足端與仿真地面的接觸類型和摩擦力，對每條腿的側擺關節、大腿關節和小腿關節添加旋轉約束和俯仰自由度，在4 條腿上添加共計12 個驅動，并將Simulink 中足端軌跡函數的逆解與這12 個驅動進行配對，以實現通過Simulink 對四足機器人的控制。在MATLAB 中添加ADAMS-sys 模塊，將設置好的ADAMS 模型導入控制系統，在MATLAB-Simulink中搭建控制平臺，并將每個關節的角度變化函數輸入到ADAMS 中[8]，設置好對應的參數后即可進行兩平臺間的聯合仿真，聯仿平臺見圖6。

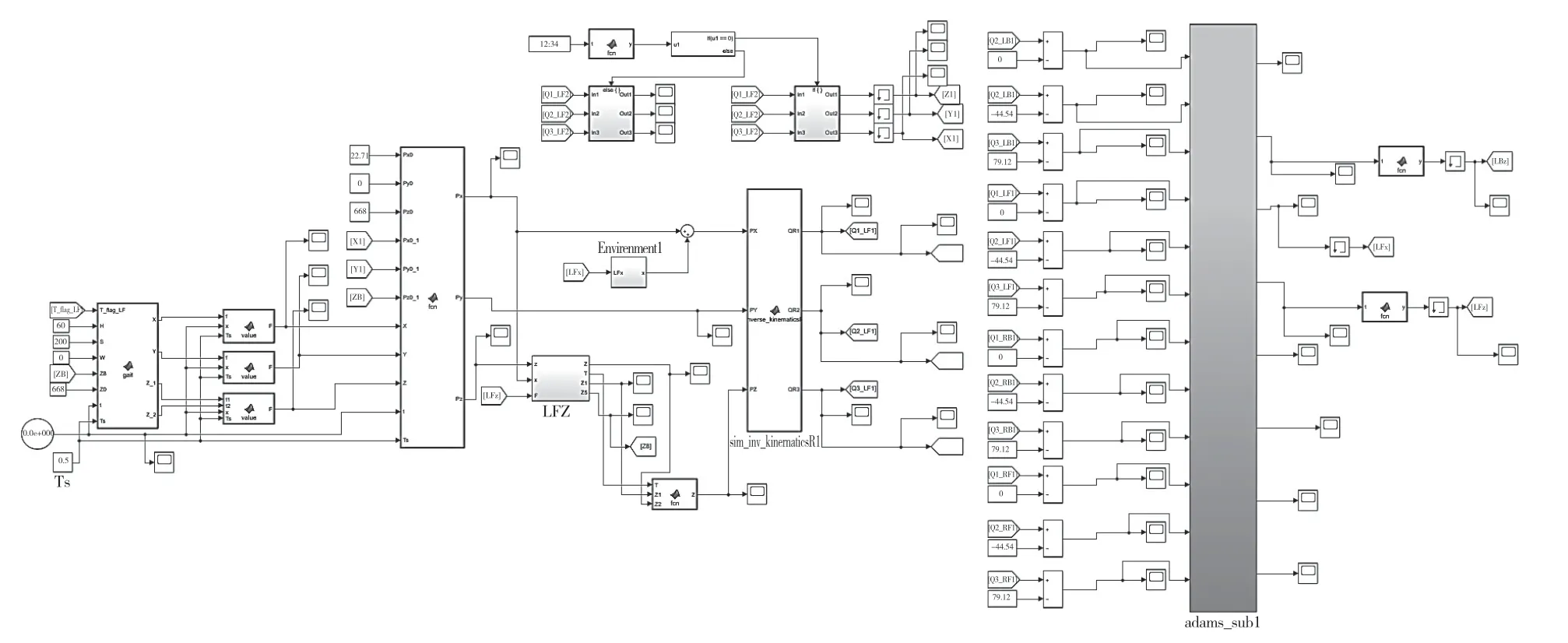
圖6 Simulink 控制臺Fig.6 Simulink console

5 仿真結果與結論分析

聯合仿真完成后，可以看到ADAMS 的仿真全過程并獲得電機轉角、關節力矩及各方向位移等數據。

坡面角度修正后的足端軌跡仿真出的質心圖如圖7、圖8 所示。

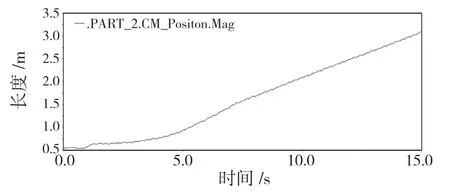
圖7 質心軌跡Fig.7 Centroid trajectory

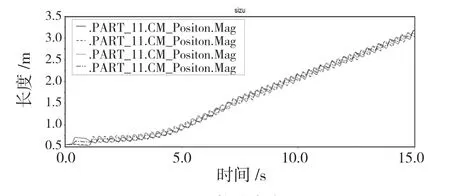
圖8 足端軌跡合方向Fig.8 Direction of foot trajectory

在30°的坡面上，開始時質心軌跡出現2次變動，分別對應橫滾角與俯仰角的反饋調整，調整后的四足機器人平穩前進，質心軌跡平滑上升，達到了穩定爬坡30°的基本要求。

俯仰角的修正圖如圖9 所示。

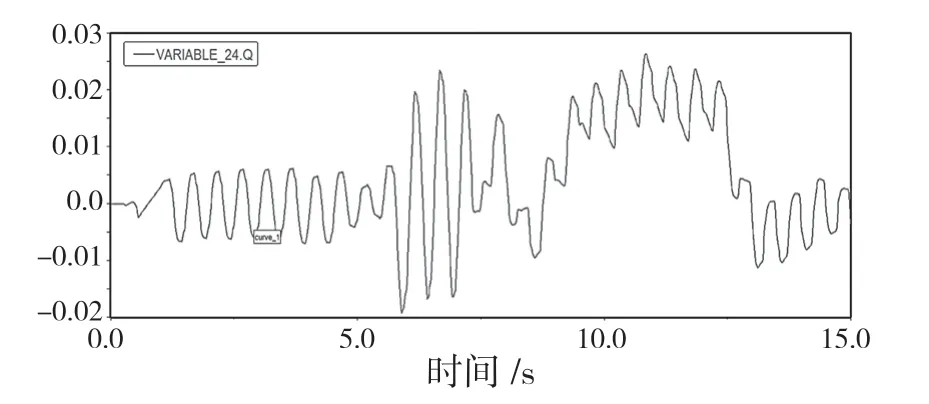
圖9 俯仰角修正圖Fig.9 Pitch angle

橫滾角的修正圖如圖10 所示。

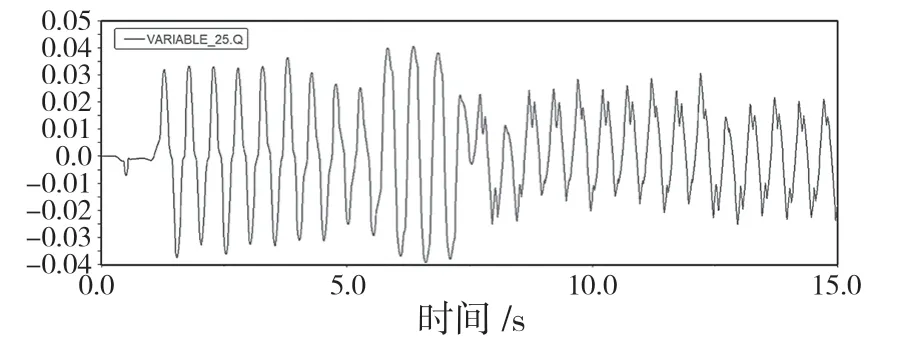
圖10 橫滾角修正圖Fig.10 Roll angle

角速度變化情況如圖11 所示。

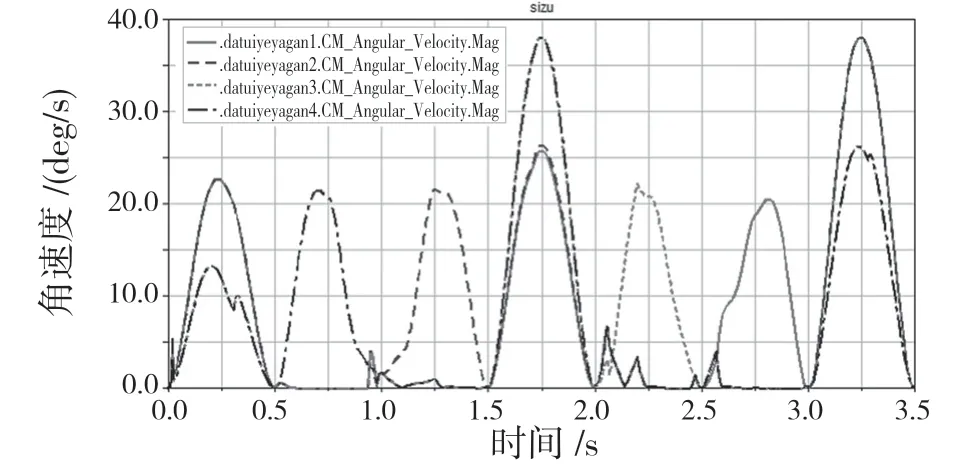
圖11 角速度Fig.11 Angular velocity

角加速度變化情況如圖12 所示。

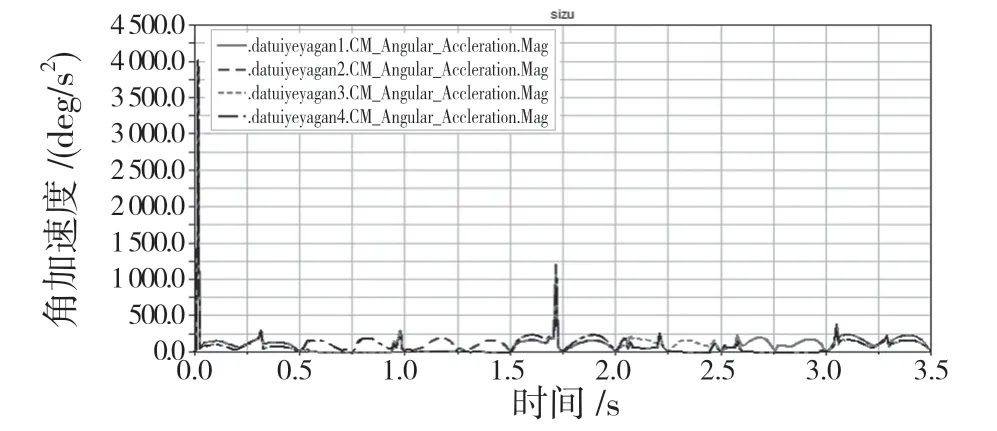
圖12 角加速度Fig.12 Angular acceleration

6 結論

從質心軌跡的變化情況可以看出，四足機器人前進穩定，經過俯仰角與橫滾角調整后能迅速進入預設修正范圍，且從俯仰角與橫滾角的修正圖可以看出，四足機器人在坡面的運動周期性良好，修正后的變化范圍較小，基本處于 0.04 之間，經過對照實驗可以看出，經橫滾角與俯仰角反饋改變的步態有效地增加了四足機器人坡面運動的穩定性，考慮到實際情況中四足左右坡面也存在著運動中的不確定性，因此后續可加入左右腿抬高距離與坡面橫向角度的數量關系做進一步的研究。