一種關于巴哈車架的建模和仿真

陳博文

（211167 江蘇省 南京市 南京工程學院）

0 引言

車架是汽車的骨架，通常用于支撐和連接汽車各個零部件；不僅要承受來自各個方向的載荷，同時還要保護車手的安全。在巴哈賽車中，車架除了用于支撐所有其他功能的系統之外，還同時兼具有防滾架的作用，增強車身總體強度、抗扭彎度等，在車體發生側翻時保護車手不受傷害，減少地面帶給車手直接的沖擊。

本文以巴哈車架為研究對象，參照2020 巴哈大賽競賽規則，采用正向設計的方案，利用有限元分析軟件對車架強度（包括靜態載荷、彎曲工況、制動工況、轉彎工況）、車架剛度（包括扭轉剛度、彎曲剛度）、自由模態的有限元仿真分析。基于軟件仿真結果得出各個工況下的應變、位移、支反力云圖，計算車架扭轉、彎曲剛度來評判車架的合理性，實現巴哈車架的建模和仿真。

1 巴哈車架材料與管件參數的確定

參照2020 巴哈大賽競賽規則中對車架材料和尺寸規格的要求：擬采用4130 合金鋼（30CrMo）為管件基準鋼鐵材料，其力學性能遠比Q235鋼高，屈服強度可達785 MPa，抗拉強度超過985 MPa；具有很高的強度和韌性；材料的基本參數：密度為7 850 kg/m3，泊松比約為0.279，楊氏模量為2.11E+11 Pa。根據2020 巴哈大賽要求，擬決定車架主要管件規格Φ25.4 mm×3.0 mm,次要管件規格Φ25.4 mm×1.7 mm[1]。

在CATIA 里先確定好桿件連接點、懸架硬點等位置的參數，初步畫出車架的空間線圖（如圖1 所示）。完成線圖后，再對線圖拔肋，分別對主要管件和次要管件按不同規格起肋管，注意在多個桿件連接處需要對該段做坡口處理，運用布爾切割把干涉段減去，保留主要桿件，避免計算時重復計算重合段質量。部分管件需要彎曲處理，彎管延伸段不得超過838 mm，且彎徑必須小于152 mm。除非添加扣板加固車架防滾環與防滾箍之間的連接，其規格參數同主要管件一致，車架總質量約為41.457 kg，初步設計的巴哈車架鋼管圖為如圖2 所示。

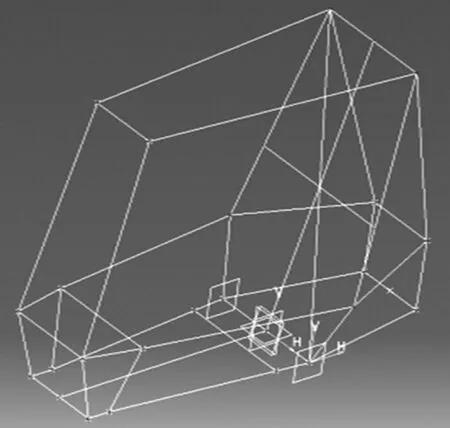
圖1 巴哈車架空間線圖Fig.1 Baja frame line diagram

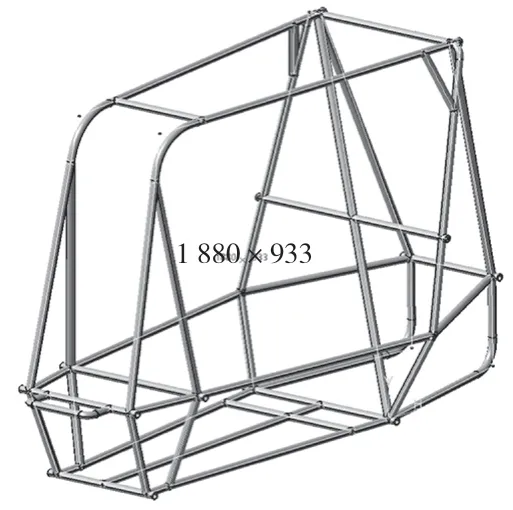
圖2 巴哈車架鋼管圖Fig.2 Baja frame steel pipe diagram

2 巴哈車架有限元仿真分析

將CATIA 保存的STP 模型導入到Workbench中，利用static structural（靜態結構）板塊完成靜態載荷、剛度分析、自由模態等多個有限元仿真。

初步設定有限元模型建立時網格尺寸為10 mm，共有5 615 個節點和2 812 個梁單元。鋼管連接方式采用焊接，保證相鄰鋼管之間節點重合，使得所有管件成為一個整體，如圖3 所示。

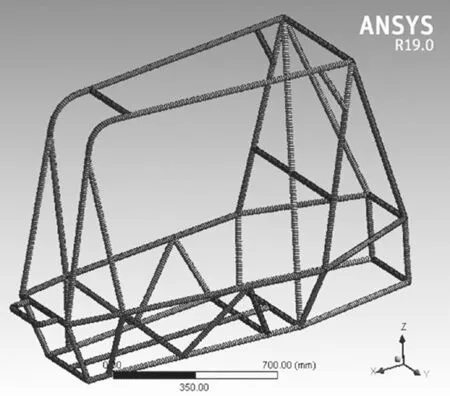
圖3 車架網格劃分Fig.3 Meshed frame

2.1 靜態載荷分析

車架所受靜態載荷包括車架自身重量、駕駛員體重、發動機、轉向系統等，在Workbench 中，通過簡化為添加重力場、集中載荷、均布載荷來達到加載靜態載荷的目的。由于車架在行駛過程中會受到動載、偏載、沖擊載荷等多種載荷類型綜合作用，考慮到車架的載荷類型多樣化，且為理想化模型，存在其他單元分擔車架所承受的載荷，因此需要進一步計算。設車架所受載荷公式為

式中：FS——等效載荷；m ——質量；g ——重力加速度，取9.8 N/m2；AS——等效載荷系數，計算載荷時取2.0～2.5，這里取2.5[2]。

可得車架所受靜態載荷情況如表1 所示。

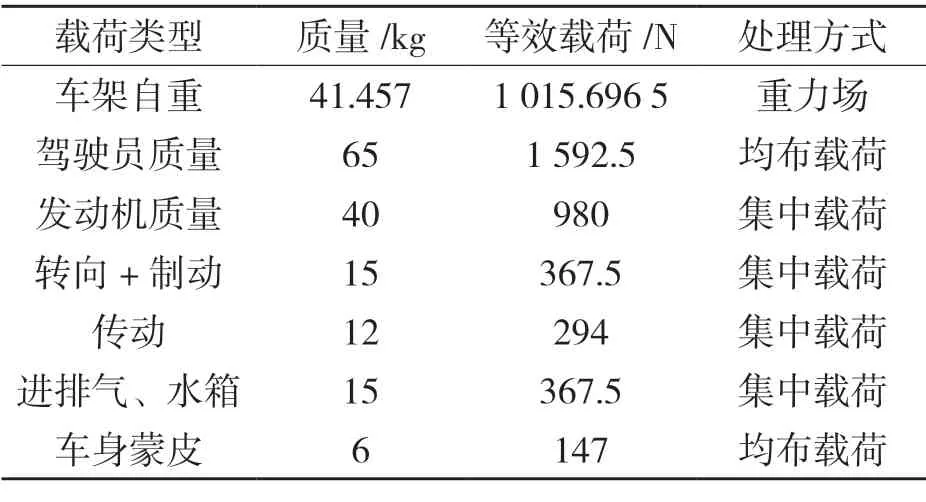
表1 車架所受靜態載荷情況Tab.1 Static load conditions on the frame

圖4 為車架在靜態載荷狀態下整體應力分布以及添加的懸架約束條件。

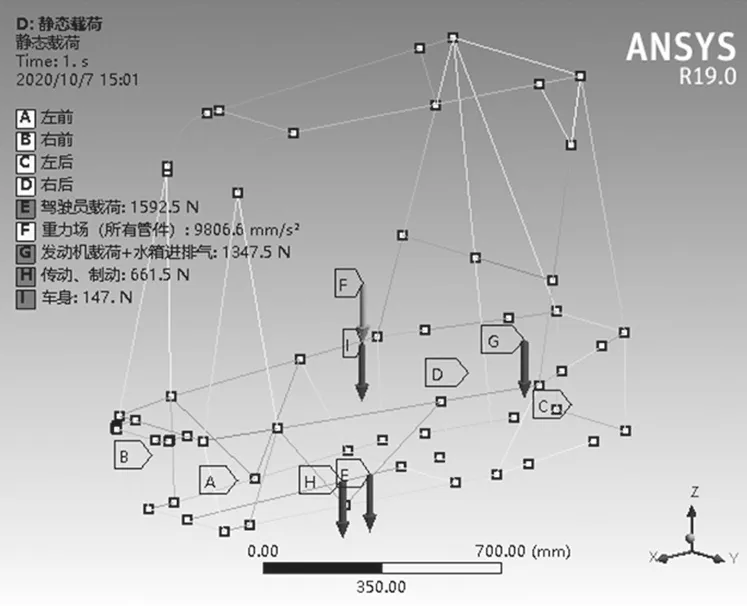
圖4 靜態載荷下車架所受約束條件Fig.4 Constraints under static load

2.2 車架強度分析

2.2.1 彎曲工況分析

為模擬車架在靜止狀態下應力分布并分析車架彎曲變形情況，以重力場、均布載荷、集中載荷等多種形式對車架進行仿真，檢驗其強度、抗疲勞能力。同樣，計算載荷時需要乘以一個等效載荷系數，通過對車架與懸架的連接點添加約束，將載荷添加到車架，實現車架彎曲工況的模擬[3]。

彎曲工況分析時，車架具體約束方式添加如表2 所示。

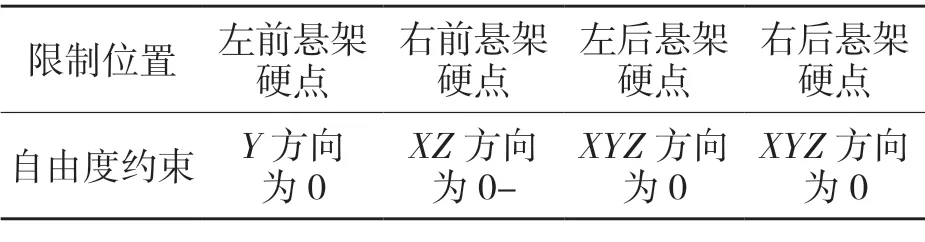
表2 彎曲工況下車架約束方式Tab.2 Frame constraints of bending conditions

經過有限元分析，車架在彎曲工況下的應力云圖如圖5 所示，最高可達2.747 6 mm；應力分布云圖如圖6 所示，最大應力為31.277 MPa，出現在防滾箍和防滾環連接處，此處多管件連接，易出現應力集中現象。遠低于4130 鋼的屈服極限785 MPa，所以車架整體存在很大的強度富余量，存在很多優化空間.

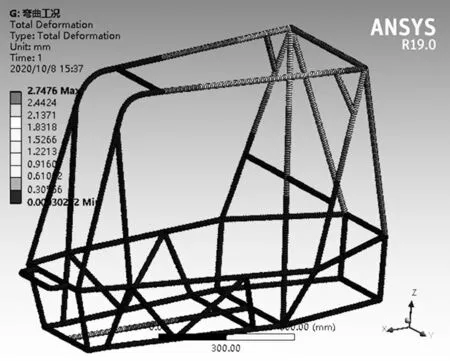
圖5 彎曲工況下的應力云圖Fig.5 Stress nephogram under bending condition

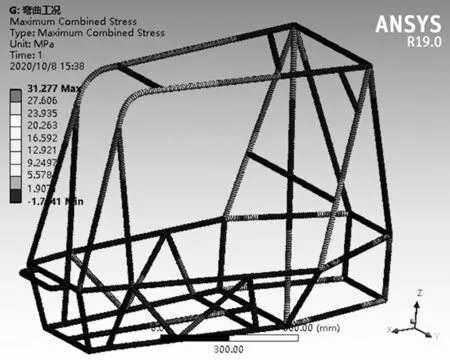
圖6 彎曲工況下的應力分布云圖Fig.6 Stress distribution nephogram under bending condition

2.2.2 制動工況分析

為模擬車架在比賽中遇緊急制動時所受載荷情況，賽車在制動時會受到一個縱向的慣性力作用。慣性力的大小由賽車和車手總體質量的大小、制動減速度決定。通過對車架施加1.4g 的制動減速度，并約束車架各個懸架硬點的自由度來實現制動工況的分析。

制動工況分析時，車架具體約束方式添加如表3 所示。

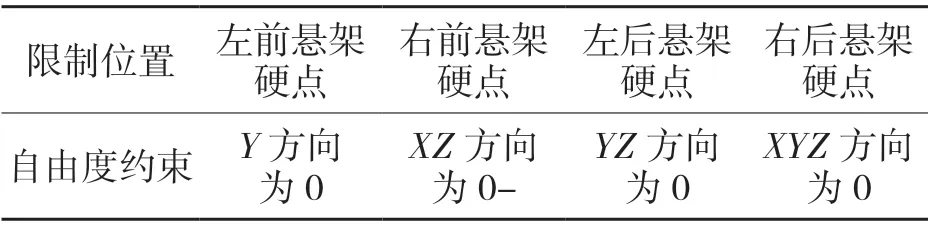
表3 制動工況下車架約束方式Tab.3 The frame constraints of braking conditions

圖7 所示為制動工況下車架的位移云圖，最大可達3.646 4 mm；圖8 所示為制動工況下車架的應力云圖，最高可達44.892 MPa，主要集中在后懸架硬點區域和防滾環焊點。

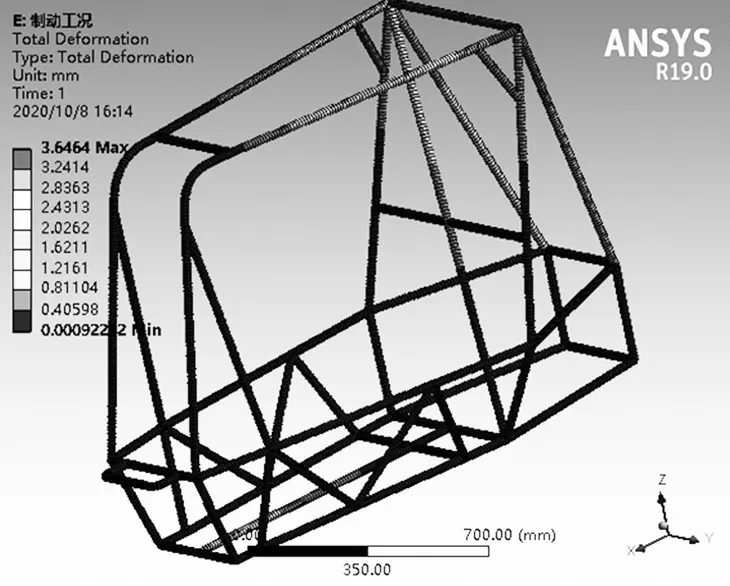
圖7 制動工況下的位移云圖Fig.7 Displacement cloud diagram under braking condition

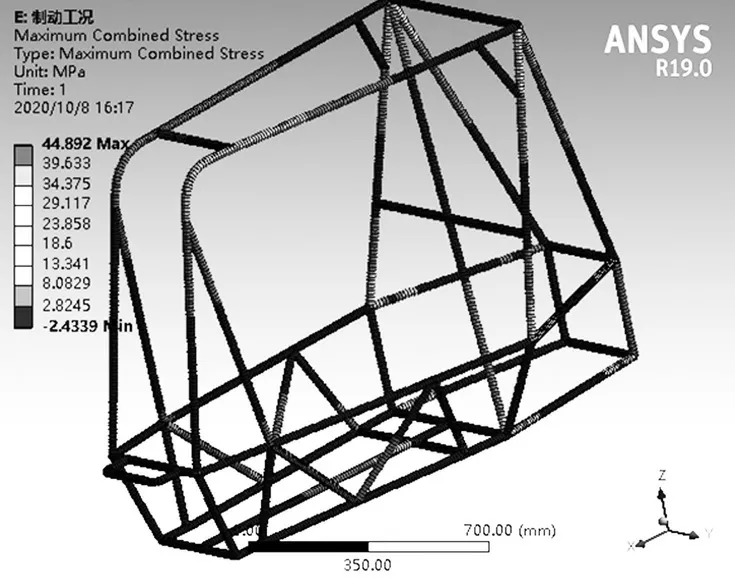
圖8 制動工況下的應力云圖Fig.8 Stress nephogram under braking condition

2.2.3 轉彎工況分析

行駛過程中，車架會因為轉向時的離心力作用受到橫向載荷，會對車架產生一個彎曲變形的作用。同時，當賽車經過坑洼路面時，產生輪跳會對車架有扭曲變形的作用。通過對車架加載離心加速度和對其懸架硬點約束來達到模擬轉彎工況分析。

轉彎工況分析時，車架具體約束方式添加如表4 所示。

表4 轉彎工況下車架約束方式Tab.4 Frame constraints of turning conditions

圖9 所示為車架在轉彎工況下的位移云圖，其最大位移量為4.658 9 mm 在防滾箍和主環連接處；圖10 所示為車架在轉彎工況下的應力分布云圖，最高可達45.287 MPa，主要集中在后懸架硬點處附近。

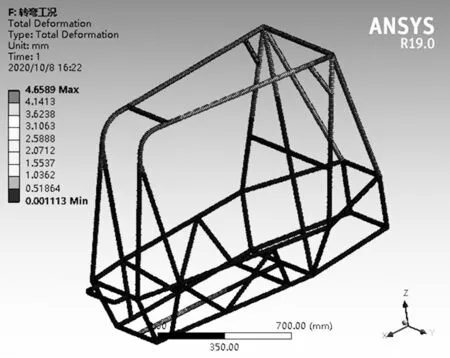
圖9 轉彎工況下的位移云圖Fig.9 Displacement cloud map under turning condition

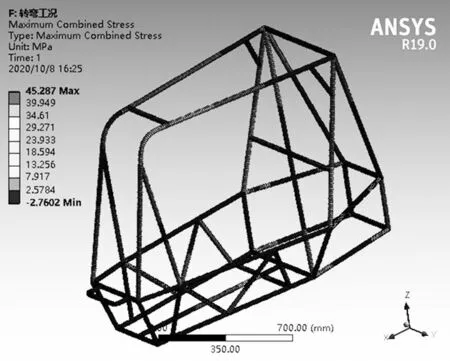
圖10 轉彎工況下的應力分布云圖Fig.10 Stress distribution nephogram under turning condition

2.3 車架剛度分析

2.3.1 扭轉剛度分析

將車架看作簡支梁，通過給車架上的左前懸架硬點和右前懸架硬點處添加相反方向的位移約束，后懸架硬點均限制方向移動，釋放所有硬點的旋轉自由度，以達到對車架實現扭轉效果。

扭轉剛度分析時，車架具體約束方式添加如表5 所示。

表5 扭轉剛度時車架約束方式Tab.5 Frame constraints of torsion stiffness

考慮到對整車扭轉剛度分析時的扭轉角度小，可利用扭轉剛度計算公式

式中：M——轉矩；θ——扭轉角度；F——支反力；l——位移約束的橫向距離；h——位移約束豎直距離。

經過有限元分析可得，在使前懸架產生1 mm 扭轉所需支反力為F=3 426.9 N，位移約束的橫向距離l=0.42 m，位移約束豎直距離h=0.02 m。解出扭轉剛度Sr=5 330.7 N·m/(°)，而一般巴哈車架扭轉剛度應大于1 000 N·m/(°)，符合設計所需要求。

其應力分布云圖如圖11 所示。可以看出，車架整體應力較低，最大應力為289.05 MPa，主要分布在前橫梁和防側撞結構件的連接處，此處為多個管件連接接口處，易產生應力集中現象，加上扭轉剛度分析時給車架一定的強制位移會產生較大應力。而4130 鋼材料的屈服極限為785 MPa，最大應力小于屈服極限，故檢驗合格[4]。

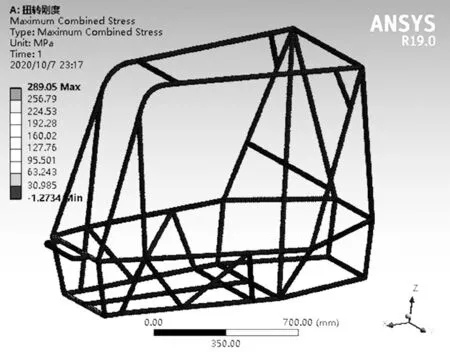
圖11 扭轉應力分布云圖Fig.11 Torsional stress distribution nephogram

其位移云圖如圖12 所示。最大位移分布在防滾箍和防滾環連接處，約為3.081 4 mm。

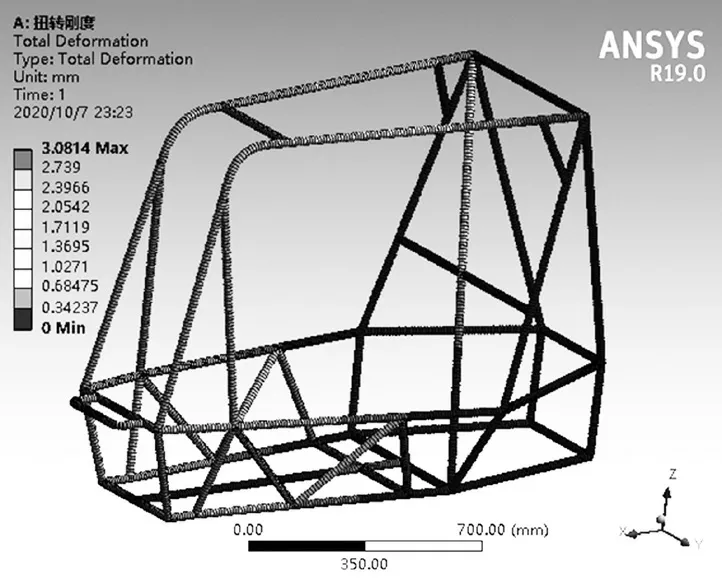
圖12 扭轉位移云圖Fig.12 Torsional displacement cloud map

2.3.2 彎曲剛度分析

將車架視作簡支梁，前懸架和后懸架的連接點作為支點，僅釋放左右前懸架Y 方向的自由度。

對車架中部區域加載壓力，最后檢測其彎曲變形程度和應力分布情況。車架具體約束方式添加如表6 所示。

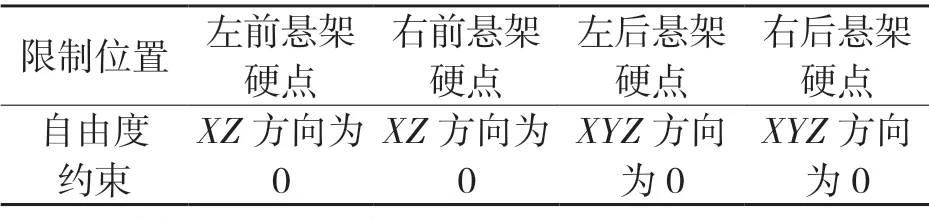
表6 彎曲剛度時車架約束方式Tab.6 Frame constraint mode for bending stiffness

計算簡支梁的彎曲剛度：

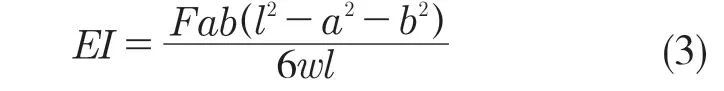
式中：F——施加的載荷；l——前后懸架硬點距離；a——施加載荷的點到前懸架硬點的距離；b——施加載荷的點到后懸架硬點的距離；w——車架底部撓度。

擬在車架中部施加一個F=5 000 N 的載荷，前后懸架硬點l=1.200 2 m，前懸架應點到施加載荷點的距離a=0.707 5，后懸架應點到施加載荷點的距離b=0.492 7。由應力云圖標尺可得撓度w=0.81×10-3m（如圖13 所示）。將數值代入式（3）可得彎曲剛度：EI=207 642 N·m2，符合彎曲剛度要求[5]。

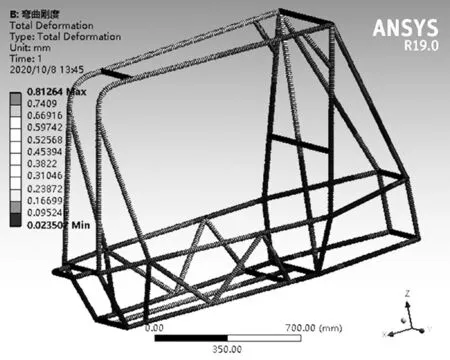
圖13 抗彎剛度作用下位移Fig.13 Displacement under bending stiffness

2.4 自由模態分析

行駛過程中，由于路面顛簸，會對車架產生激發振動，發動機工作時自身又會產生震動。當兩種震動頻率相同時會出現共振現象，從而對車架造成較大的損害。利用Workbench 中的模態分析板塊，對車架進行自由模態分析，即采用自由邊界的方法，不添加任何的外部載荷和約束對車架分析。

賽車行駛過程中，兩個主要的激振源由來分別是路面激勵和發動機激振。巴哈賽車選用的發動機是Briggs &Stratton 10 HP OHV Vanguard 19的未經改裝單缸四循環風冷發動機，怠速狀態下發動機轉速約為1 750 r/min，最高轉速狀態下約為3 600 r/min。參考發動機激勵頻率公式，分析發動機振動的頻率范圍。

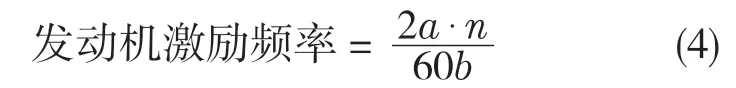
式中：a——發動機的缸數；n——發動機的轉速，r/min；b ——發動機沖程數。

由式（4）得發動機激勵頻率為14.58～30 Hz，相較于車架自由模態分析頻率，由于前6 階為剛體模態，頻率幾乎為0，到第7階時出現了車架的固有頻率。理論上，車架的前幾階頻率是最容易激發出來的，隨震動階次的提高，模態越難以被激發出來[6]。

經過自由模態分析可得，車架總體震動頻率均高于發動機激勵頻率，不會引起共振現象。

3 結論

本文以2020 巴哈大賽競賽規則為基本，詳細闡述了巴哈車架在CATIA、ANSYS 中的建模分析方法，并對車架進行有限元靜力學分析。仿真結果表明：該車架在各種工況下都能基本滿足強度和剛度要求。綜合彎曲工況、制動工況、轉彎工況三大工況下的車架應力分布情況可知：應力主要集中在發動機艙的后懸架硬點處，且管件連接點可能會出現應力集中現象，加劇管件的變形，需對目標管件進行加固處理；從扭轉剛度、彎曲剛度的分析結果可知：車架整體結構仍有一定優化空間，仍有一定的剛度富裕量，整體架構還可進一步實現空間拓撲優化,適當減小次要管件的尺寸使得整車車架實現輕量化，從而降低車架的整體質量。