考慮剪應力水平和土體干密度影響的錨-土界面剪切蠕變模型

陳昌富，溫永凱，朱世民

（1.建筑安全與節能教育部重點實驗室（湖南大學），湖南 長沙 410082；2.湖南大學 土木工程學院,湖南 長沙 410082）

在實際工程中，預應力錨桿都會產生不同程度的應力松弛和蠕變，其中錨固體與巖土體界面的剪切蠕變是產生這種現象的主要原因.為此，國內外部分學者通過室內外試驗對錨固體-巖土體界面的剪切蠕變特性開展了研究.Kim[1]通過開展土層灌漿錨桿的拉拔蠕變試驗和應力松弛試驗，分析了錨桿的蠕變速率和應力損失；伍國軍等[2]基于混凝土-花崗巖界面剪切蠕變試驗結果，提出了一種基于經驗的非線性剪切蠕變模型；陳昌富等[3-4]根據錨固單元體蠕變試驗曲線，建立了具有良好擬合及預測效果的錨-土界面經驗蠕變模型和分數階導數Burgers模型.

相對于界面蠕變研究而言，國內外很多學者開展了巖土體的三軸[5-8]、直剪[9]等蠕變試驗，建立了各種蠕變模型.比如，經驗蠕變模型有Singh-Mitchell模型[10]、Mesri 模型[11]、盧萍珍等[6]提出的改進模型；而元件模型則有各類元件的串并聯模型[12].

目前關于蠕變特性的研究，多數只利用單組蠕變試驗曲線建立模型，模型中僅考慮了單個因素(即剪應力水平)對蠕變的影響.實際工程中，無論是巖土體，還是錨-土界面都是在多因素（應力水平、巖土體性質、環境條件或者注漿壓力等）影響下產生剪切蠕變，而目前除考慮應力水平外還考慮其他因素影響的蠕變模型的研究相對較少.對于巖土體，有學者開展了除應力水平外還考慮含水率[13]、溫度[14]及凍融循環[15]等因素影響下的蠕變模型研究.對于錨-土界面，雖然陳昌富等[16]開展了不同注漿壓力下錨固體-紅黏土界面剪切蠕變試驗，并基于Kriging 模型建立了可同時考慮剪應力水平和注漿壓力影響的錨-土界面剪切蠕變模型，但目前尚未見有同時考慮剪應力水平和土體干密度影響的錨-土界面剪切蠕變模型的研究.

此外，現有的巖土體蠕變模型或界面剪切蠕變模型基本都是根據分別加載蠕變曲線建立的，而基于蠕變等時曲線來建立蠕變模型的研究尚未見文獻報道.

為探究土體干密度對錨固體-紅土界面剪切蠕變特性的影響，本文開展了不同土體干密度的錨-土界面分級加載蠕變試驗，利用陳宗基等[17]提出的蠕變曲線處理方法得到了分別加載蠕變曲線，并通過“等時曲線法”獲得不同土體干密度的錨-土界面長期抗剪強度.利用雙曲線模型對部分被選應力水平下的蠕變等時曲線進行回歸分析，然后建立出雙曲線模型參數與土體干密度和時間的經驗關系，據此進一步建立出可同時考慮剪應力水平和干密度影響的錨-土界面剪切蠕變模型.最后，利用本文模型對參與及未參與確定建模參數的蠕變曲線進行預測，以驗證模型預測精度.

1 不同干密度下錨-土界面蠕變試驗

1.1 試驗用料

試驗所用土料為衡陽盆地紅層風化殘積土，取自湖南省祁東縣某邊坡開挖現場，其主要物理力學參數為：天然含水率w=30.7%，天然干密度ρd=1.23 g/cm3，液限wL=54.3%，塑限wp=35.3%，塑性指數Ip=19，比重ds=2.680，最大干密度ρmax=1.55 g/cm3，最優含水率wop=26.5%.試驗土料不均勻系數Cu=16.67，曲率系數Cc=1.13，屬于級配良好.

1.2 試驗方案及裝置

試樣含水率w 均為26%，土體干密度ρd設置4個水平，分別為1.1 g/cm3、1.2 g/cm3、1.3 g/cm3和1.4 g/cm3，對應的飽和密度ρsat（飽和度Sr）分別為：1.69 g/cm3（0.485）、1.75 g/cm3（0.565）、1.81 g/cm3（0.656）和1.88 g/cm3（0.762）.需說明的是，每組試驗均制作2個平行試樣，分別用來開展瞬時拉拔試驗和蠕變試驗.

試樣直徑D 為30 cm，高度H 為10 cm，錨孔直徑d為4.8 cm.試樣直徑與錨孔直徑之比D/d=6.25>5，因此，邊界效應對試驗結果的影響可忽略不計[18].

實際錨固工程通常以鉆孔方式形成錨孔，為模擬實際成孔方式，本文對文獻[19]的制樣方法進行了改進，設計制作了一套螺旋干鉆法成孔的錨固單元體試樣制備裝置，如圖1 所示.

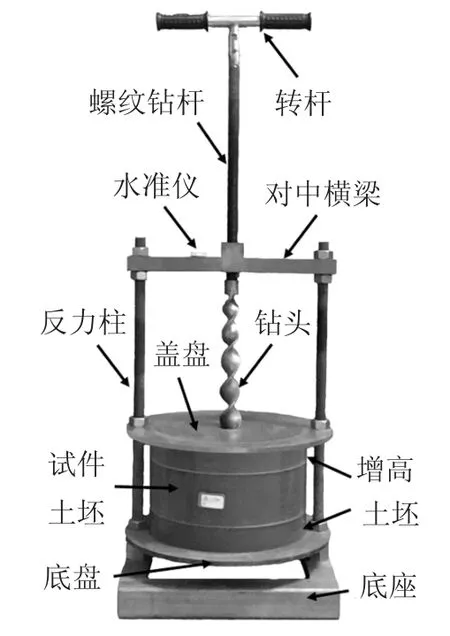
圖1 鉆孔裝置Fig.1 Drilling device

基于滑輪組增力原理設計制作了蠕變拉拔試驗裝置，其增力效率為2 倍，即試樣承受的拉拔力是加載砝碼質量的2 倍.該裝置由蠕變加載系統和數據采集系統兩部分組成，具體結構如圖2 所示.

圖2 錨-土界面剪切蠕變試驗系統Fig.2 Device for testing anchor-soil interface creep behavior

1.3 試驗方法

試驗流程包括土坯制作、鉆孔成孔、灌漿及試樣養護以及蠕變加載等，具體如下：

1）土坯制作.利用自行研制的制樣裝置[19]，對含水率為26%的重塑紅土料按控制干密度的方式進行分層擊實，以此制備土坯.

2）鉆孔成孔.首先，將土坯放置到鉆孔裝置的底盤中間，并利用一內徑略大于錨孔直徑的蓋盤固定土坯；然后，轉動鉆桿使直徑為48 mm 的鉆頭以10 r/min 的速率向下鉆土；鉆穿土坯后，回轉鉆桿，提出鉆頭，即獲得以鉆孔方式成孔的試樣.需注意的是，為確保鉆孔所成錨孔的均勻性，鉆孔前，在土坯的上下面各設置高度為5 cm 的增高土坯.觀察錨孔可知，孔壁呈細螺紋狀，粗糙度較大.

3）灌漿及試樣養護.首先，將Φ16 mm 螺紋鋼筋豎直放置在錨孔中心；然后，將水泥砂漿（m水∶m灰∶m砂=0.45 ∶1 ∶1）灌入錨孔并振搗密實；水泥砂漿初凝后，將試樣移至密封袋中養護28 d.

4）試樣蠕變加載.蠕變試驗的加載方式為分級加載.具體地，預先制作平行試樣，并測定其瞬時剪切強度，再基于荷載比例（蠕變荷載與瞬時剪切強度之比）的分級方法設定蠕變加載等級為7～8 級.由于筋體-注漿體界面強度遠大于錨固體-土體界面強度，因此筋體-注漿體界面不會發生剪切位移.這樣，本文測定的筋體位移便為錨-土界面剪切位移，如圖2 所示.此外，本試驗選用的蠕變穩定標準為連續24 h 內剪切位移增量小于0.01 mm[20].

2 試驗結果及分析

對試樣進行蠕變加載，獲得分級加載全過程曲線.利用陳宗基等[17]提出的蠕變曲線處理方法獲得了分別加載蠕變曲線，得到分別加載條件下剪切位移u 與時間t 的關系曲線，如圖3 所示.

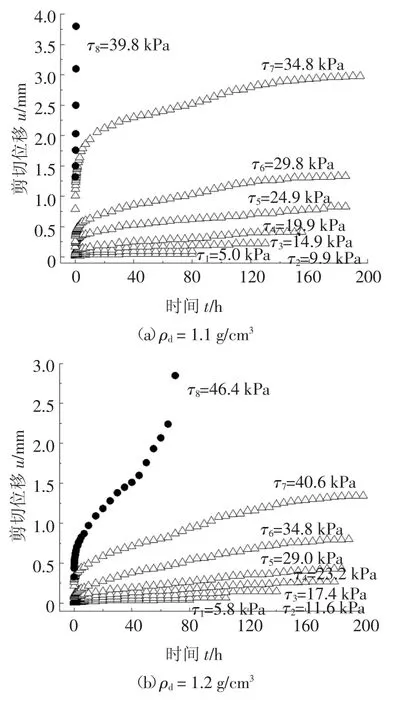
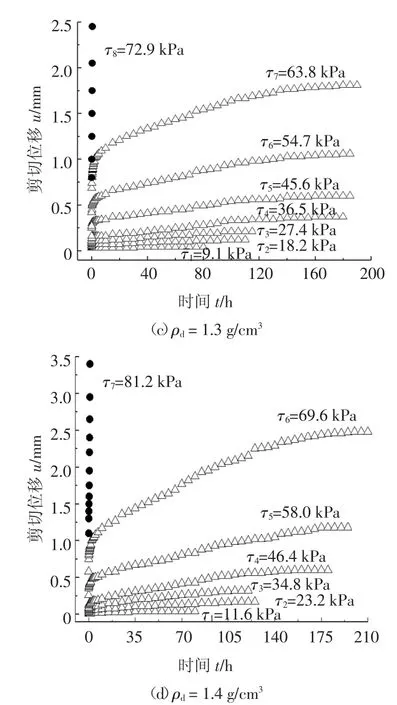
圖3 分別加載蠕變曲線Fig.3 Shear creep curves in different stress levels

由圖3 可知，土體干密度對錨-土界面剪切蠕變特性影響顯著.拉拔荷載相近時，隨著干密度的增大，錨-土界面剪切蠕變位移減小，蠕變穩定時間變短.例如，剪應力近似為35 kPa 時，土體干密度從1.1 g/cm3增加至1.4 g/cm3，錨-土最終界面剪切蠕變位移u 由3.0 mm 減小至0.25 mm，蠕變穩定時間由160 h 縮減至70 h.

繪制各組試樣在t 為0 h、0.5 h、1 h、2 h、5 h、10 h、20 h、40 h、60 h、80 h、100 h 和120 h 時的蠕變等時曲線，如圖4 所示.將各組試樣等時曲線轉折點（該轉折點對應的應力即為錨-土界面屈服應力，當荷載大于屈服應力后，剪切位移會顯著增加，此時錨-土界面由黏彈性狀態轉向黏塑性狀態）連線的水平漸進線在縱軸（剪應力τ 軸）上的截距作為錨-土界面長期抗剪強度τ∞.繪制土體干密度ρd與錨-土界面長期抗剪強度τ∞及瞬時抗剪強度τf關系曲線，如圖5 所示.

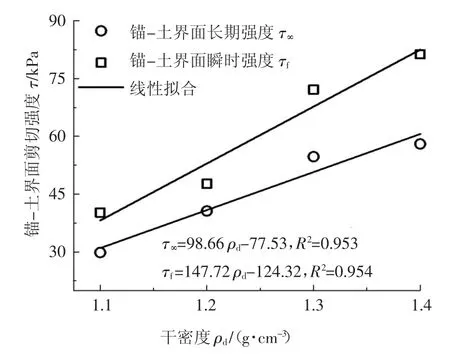
圖5 錨-土界面長期強度τ∞、瞬時強度τf 與干密度關系Fig.5 Relationship curves of anchor-soil interface long term strength and instantaneous strength versus dry density

由圖4 可知：①各組試樣的等時曲線均呈非線性，曲線形狀類似于雙曲線；②土體干密度ρd越小、時間t 越大，等時曲線非線性特征越明顯.

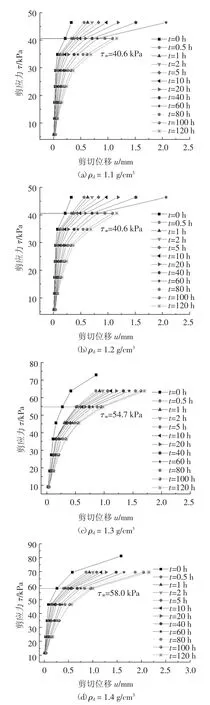
圖4 剪應力τ-剪切位移u 等時曲線Fig.4 Isochronal curves of shear stress（τ）-displacement（u）

由圖5 可知，錨-土界面長期抗剪強度τ∞和瞬時抗剪強度τf均隨土體干密度ρd的增加而增加，兩者大致呈線性關系.因此，為簡化起見，本文以線性擬合的方式建立錨-土界面剪切強度隨土體干密度變化經驗公式.可以看出，錨-土界面長期抗剪強度τ∞約為其瞬時抗剪強度τf的60%～80%.

3 錨-土界面雙曲線剪切蠕變模型

錨-土界面剪切蠕變等時曲線實際上就是某一時刻下的剪應力-剪切位移曲線.本文試驗結果表明，蠕變等時曲線的曲線形狀類似于雙曲線，且不同土體干密度和不同時間對應的等時曲線的曲線形態不同.因此，如果利用雙曲線模型對等時曲線進行回歸分析，然后建立雙曲線模型參數與土體干密度和時間的經驗關系，就可以進一步建立出考慮剪應力水平和干密度影響的錨-土界面剪切蠕變模型.基于該建模思路，下面以干密度ρd=1.3 g/cm3試樣的衰減蠕變試驗曲線為例來探討錨-土界面衰減蠕變模型的建模方法及其合理性.

3.1 錨-土界面剪切雙曲線蠕變模型

雙曲線模型具有參數少、物理意義明確等優點，其方程為：

式中：τ 為錨-土界面剪應力；u 為界面剪切位移；a、b為模型參數.

定義初始剪切模量G0為錨-土界面剪應力-剪切位移等時曲線在剪應力為0 處的斜率，界面極限抗剪強度τult為等時曲線漸近線對應的極限值.由式（1）可知，模型參數a 和b 分別代表G0和τult的倒數.對于同一試樣不同時刻下的等時曲線，對應有不同的G0和τult.因此，參數a 和b 與時間t 相關，假定符合一定的函數關系：

將式（2）代至式（1），可得到考慮時間效應的錨-土界面剪切雙曲線模型，再對其進行變換，即可建立出錨-土界面剪切雙曲線蠕變模型：

3.2 錨-土界面蠕變模型參數辨識方法

下面就采用土體干密度為1.3 g/cm3的錨-土界面衰減蠕變試驗結果（圖3（c）），來闡述如何確定本文提出的雙曲線蠕變模型參數.

首先，利用式（1）分別對應力水平為τ1、τ3、τ4、τ6和τ7的蠕變等時曲線進行回歸分析，擬合結果見圖6，模型參數a 和b 如表1 所示.

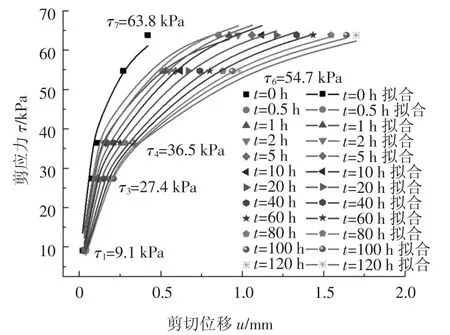
圖6 等時曲線擬合結果（干密度為1.3 g/cm3）Fig.6 Fitting results of isochronal curves（ρd=1.3 g/cm3）

由表1 可知，土體干密度ρd=1.3 g/cm3的試樣的等時曲線擬合相關指數R2均大于0.99，這表明雙曲線模型對本文蠕變等時曲線具有較好的擬合效果.此外，還可以看出，模型參數1/a 隨時間t 的增加而減小，兩者大致呈雙曲線函數形式；模型參數b 隨時間t 的變化不顯著.

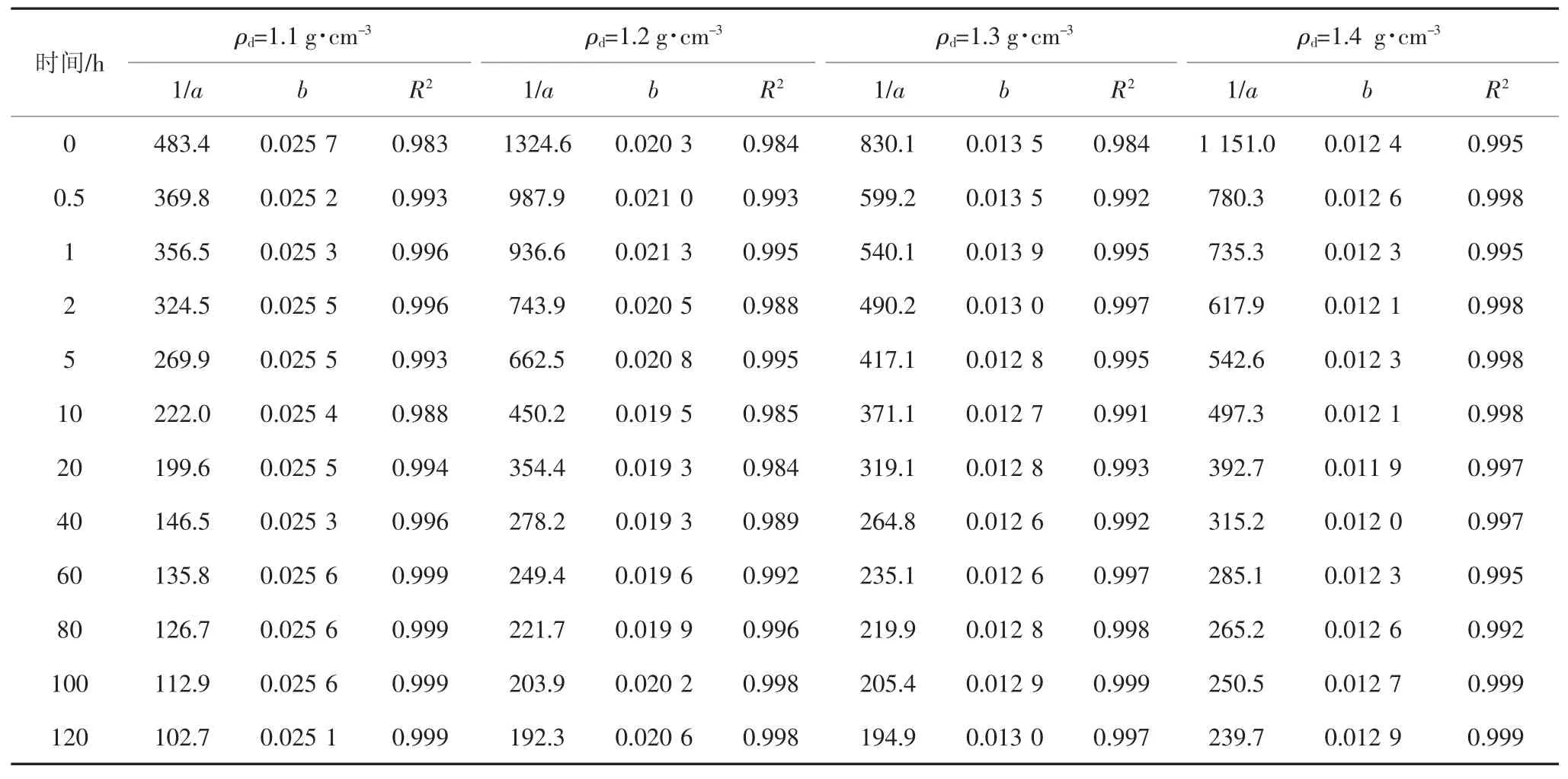
表1 各組干密度下等時曲線擬合結果Tab.1 Fitting results of isochronous curves for all specimens in different dry density

鑒于此，采用式（4）所示雙曲線函數描述模型參數a 隨時間的變化關系，而模型參數b 取均值bu.

式中：A、B、C、D 為待定參數.

采用式（4）對參數a 隨時間t 變化曲線進行擬合，得到：

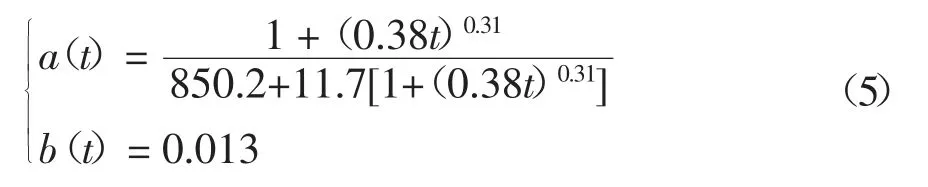
將式（5）代入式（3），即可得到土體干密度ρd為1.3 g/cm3的錨-土界面剪切蠕變模型：

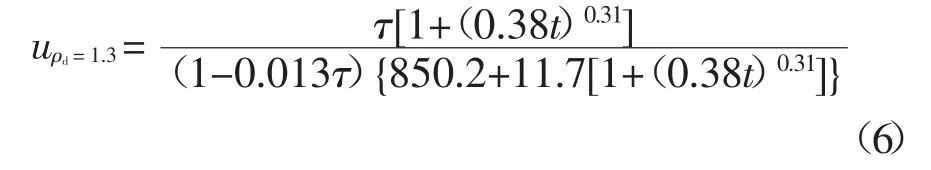
為驗證所建模型的蠕變預測效果，利用式（6）對參與建模（應力水平為τ1、τ3、τ4、τ6和τ7）及未參與建模（應力水平為τ2和τ5）的蠕變試驗曲線進行預測，結果如圖7 所示.

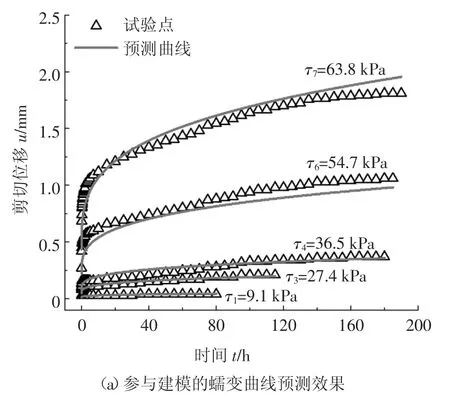
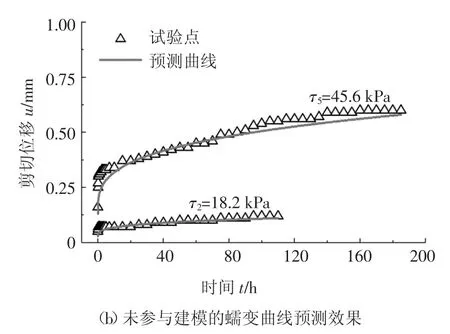
圖7 蠕變曲線預測效果（干密度為1.3 g/cm3）Fig.7 Prediction results of creep curves（ρd=1.3 g/cm3）

由圖7 可知，低應力水平下的蠕變曲線預測效果稍好于高應力水平下蠕變曲線預測效果.但整體而言，無論是參與還是未參與建模的蠕變曲線，本文提出的雙曲線蠕變模型的預測效果均較好.

3.3 不同干密度下錨-土界面蠕變模型

采用上述建模方法，對其余3 組試樣（干密度分別為1.1 g/cm3、1.2 g/cm3和1.4 g/cm3）的蠕變試驗結果進行分析，并建立出相應的蠕變模型.而且，這3組試樣也均選用應力水平為τ1、τ3、τ4、τ6和τ7的蠕變試驗數據進行建模，其余試驗數據用以模型預測.

這3 組試樣的蠕變等時曲線擬合結果如表1 所示.雙曲線模型參數a 隨時間t 變化關系的擬合結果及模型參數b 的均值bu如表2 所示.最后，將表中參數回代至式（4）和式（3），即可得到各組干密度下錨-土界面剪切雙曲線蠕變模型.

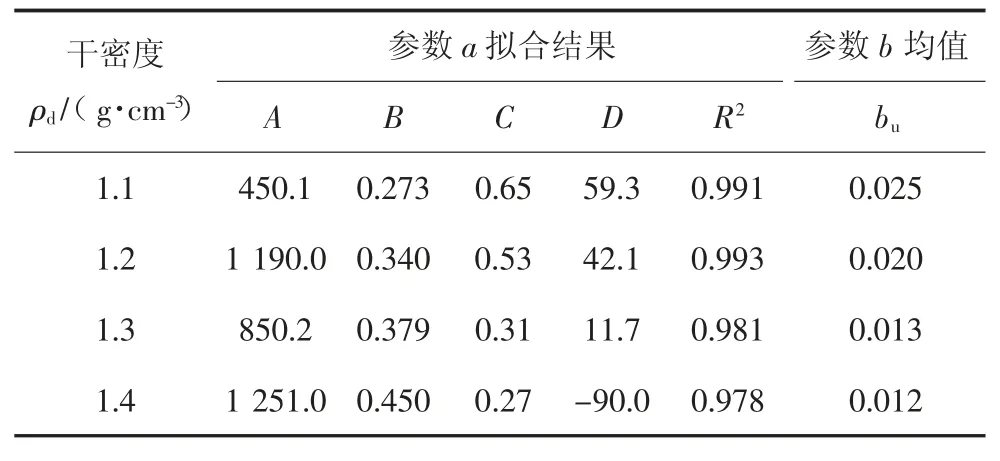
表2 模型參數擬合結果Tab.2 Fitting results of model parameters

獲得其他3 組試樣的錨-土界面剪切雙曲線蠕變模型如下：

4 考慮剪應力水平和土體干密度影響的錨-土界面剪切蠕變方程

第3 節針對4 組不同土體干密度的試樣，分別建立了僅考慮剪應力水平影響的錨-土界面剪切雙曲線蠕變模型.由表2 可知，蠕變模型參數A、B、C、D 和bu均與土體干密度相關，于是通過回歸分析可得到模型參數A、B、C、D 和bu與土體干密度的函數關系式，將其代入式（4）和式（3），便可得到同時考慮剪應力水平和土體干密度影響的錨-土界面剪切蠕變模型如下：

利用本文所建立的同時考慮剪應力水平和干密度影響的錨-土界面剪切蠕變模型，分別對土體干密度為1.1 g/cm3、1.2 g/cm3和1.4 g/cm3的蠕變試驗曲線進行預測，獲得參與建模的蠕變曲線預測效果如圖8 所示，未參與建模的蠕變曲線預測效果如圖9所示.

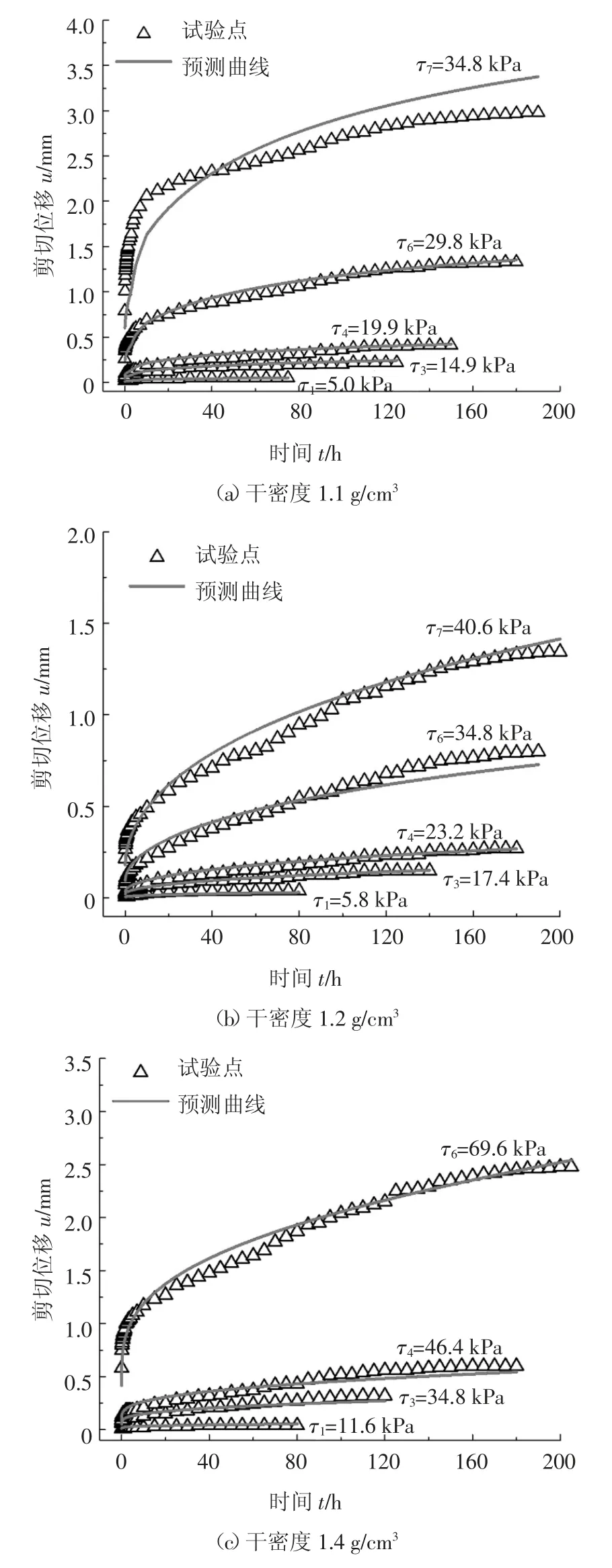
圖8 參與建模的蠕變曲線預測結果Fig.8 Prediction results of creep curves which participated in modeling

圖9 未參與建模的蠕變曲線預測結果Fig.9 Prediction results of creep curves which not participated in modeling

由圖8 和圖9 可知，隨著剪應力水平的提高，本文建立的同時考慮剪應力水平和干密度影響蠕變模型，無論是對已參與建模還是未參與建模的蠕變曲線，其預測效果均較好，這表明本文模型能夠綜合考慮土體干密度和剪應力水平對錨-土界面剪切蠕變特性的影響，具有較強的適用性和較高的預測精度.

5 結論

1）為探究土體干密度對錨固體-紅土界面剪切蠕變特性的影響，研制了螺旋干鉆成孔的錨固單元體試樣制樣裝置以及基于滑輪組增力原理的試樣蠕變加載裝置，以此開展了4 組不同土體干密度的錨固單元體試樣界面剪切蠕變試驗，獲得分級加載蠕變全過程曲線.

2）土體干密度對錨-土界面剪切蠕變特性影響顯著.應力相近時，干密度越大，錨-土界面剪切蠕變位移越小，蠕變穩定的時間越短.此外，隨著土體干密度的增加，錨-土界面長期抗剪強度呈線性增長，錨-土界面長期抗剪強度約為其瞬時抗剪強度的

60%～80%.

3）利用雙曲線模型對部分應力水平下的蠕變等時曲線進行回歸分析，然后建立雙曲線模型參數與土體干密度和時間的經驗關系，以此進一步建立出了同時考慮剪應力水平和干密度影響的錨-土界面剪切蠕變模型.結果表明，本文模型對參與建模還有未參與建模的蠕變曲線的預測效果均較好.