基于改進KNN-DPC算法的科技創新人才分類研究*

張文宇 劉 嘉 楊 媛 朱鈺婷 于 瑞

（1.西安郵電大學經濟與管理學院 西安710061）（2.中國航天系統科學與工程研究院 北京 100081）

1 引言

黨的十九大報告提出，人才是實現民族振興、贏得國際競爭主動的戰略資源。科技創新人才作為從事系統性科學和技術知識的發現、生產和應用活動的創造性人力資源，是科學技術這一先進生產力的集中體現。對于各個領域存在的科技創新人才，要充分發揮其具備的能力和素質，就要對科技創新人才進行精準分類。因此，研究科技創新人才的分類問題對我國科技創新人才的發展、社會化建設有著十分重要的作用。目前，科技創新人才的理論研究大多集中在培養階段，楊穎［1］基于新的時代背景構建出科技創新人才的培養機制。彭干三［2］在產學研融合視角下對我國科技創新人才培養過程中存在的問題提出意見。然而，科技創新人才的分類問題研究相對較少，陸一［3］等提出了三種選拔與培養類型的二維分類體系，以此來探究高校背景下創新人才的培養分類模式。邴浩［4］提出了一種政策分類的新方法來提升高校創新人才分類過程中政策的實施效果。以上的相關研究大部分是基于理論的定性研究階段，相關的定量研究很少，這導致科技創新人才分類研究的量化和精細化不足，不能充分挖掘科技創新人才的數據信息，從而對實際中科技創新人才的分類指導性不強。

在大數據背景下，充分利用海量數據資源，突出量化分析是科技創新人才分類研究的重要發展方向。因此，通過對科技創新人才數據的收集，從而對樣本數據進行數據挖掘與分析是提高人才分類效果的重要途徑。已有的研究表明聚類算法是數據挖掘中研究分類問題的有效方法，傳統聚類算法可被劃分為分割聚類、密度聚類，以及基于傳播的方法等［5～7］。Alex Rodriguez和Alessandro Laio［8］提出的一種密度峰值聚類算法DPC，該聚類算法具有計算速度快，無需迭代等特點，可以很好地描述數據分布，同時在算法復雜度上也比一般的K-means算法的復雜度低。盡管DPC算法優勢明顯，但其對高維數據的處理以及非中心點的歸類仍存在一些局限，針對DPC算法的缺點，近兩年許多學者都對DPC算法進行改進。張偉［9］將DPC算法和Chame-leon算法的優點相結合提出了E_CFSFDP算法，雖避免了將包含多個密度峰值的一個類聚成多類，但其計算量大且不利于處理高維數據。謝娟英［10］提出兩種基于K近鄰的樣本分配策略的快速密度峰值算法KNN-DPC，其算法對噪聲數據具有非常好的魯棒性，但由于該算法的聚類過程與DPC相同，故DPC算法的缺陷在該算法中仍存在。

針對上述問題，本文提出的結合主成分的改進K近鄰優化的密度峰值聚類算法IKDPC將主成分分析法融入聚類算法中對高維數據降維，克服了聚類算法中高維數據對聚類結果的影響，為了更好地描述每個樣本在空間中的分布情況給出了新的局部密度的計算方法，并對原有樣本點的分配過程進行了改進，有效提高了算法的聚類結果，使該算法能更好地應用于實際分類領域。首先，本文在闡述科技創新人才的定義及內涵的基礎上，定性分析出科技創新人才的特點并構建出科學合理的評價指標體系；然后，通過IKDPC算法對科技創新人才進行量化分類研究，根據收集資料和調研獲得的樣本評價指標數據，對科技創新人才進行實例驗證并分析其結果，并通過IKDPC算法與其他算法的分析比較表明IKDPC算法的優勢，從而為提高科技創新人才培養過程中人才層次分類的效果提供依據。

2 科技創新人才及其評價指標體系

2.1 科技創新人才的定義及內涵

科技創新人才是從事系統性科學和技術知識的生產、促進、傳播和應用活動的創造性人力資源［11］。根據科技創新人才的定義可知科技創新人才具體應包括以下五部分內涵。

1）具有較高的知識修養水平；

2）具有積極的創新實踐能力；

3）具有良好的環境適應能力；

4）具有健康的身體狀況；

5）具有健全的心理與人格素質。

2.2 科技創新人才的評價指標體系

本文對科技創新人才的素質從知識修養水平、創新實踐能力、環境適應能力、身體狀況和心理與人格素質五個部分構建評價指標體系，再根據對相關文獻和資料的研究，確定這五個部分的三級指標［12］。科技創新人才評價指標體系如表1所示。

表1 科技創新人才評價指標體系

3 DPC算法

DPC算法通過搜索合適的局部密度較大的點作為類簇中心，再將類簇的標簽從高密度點向低密度點依次傳播來實現數據樣本的聚類劃分。該算法能夠快速發現任意形狀數據集的密度峰值，并高效進行樣本點分配和離群點剔除［11］。DPC算法引入了樣本數據點xi的局部密度ρi和數據點xi到局部密度比它大且距離它最近的樣本數據點xj的距離δi，其定義如式（1）和（2）所示：

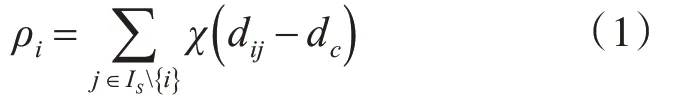
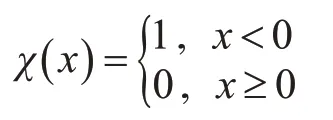
數據集，IS={1,2,…,N}，為相應指標集，dij=dist(xi,xj)表示數據點xi和xj之間的歐式距離。參數dc＞0為截斷距離。

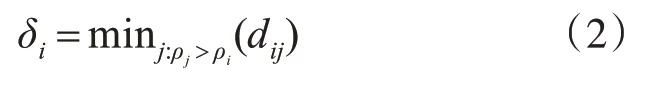
對于ρi最大的樣本數據點xi，其δi=minjdij。

對于較小的數據集，由式（1）估計的密度可能會受統計誤差的影響，此時采用式（3）來估計其局部密度［9］。

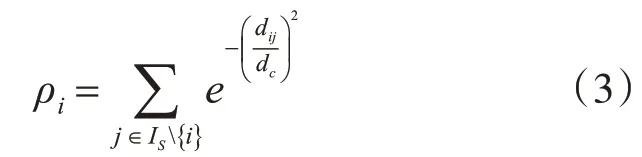
為了獲取數據的聚類中心，DPC算法首先將每個點的ρ值和δ值于坐標平面內繪制出，然后將ρ值和δ值都較大的點作為聚類中心［8］。然而，對于分布稀疏的數據，通過ρ值和δ值難以確定其聚類中心，此時DPC算法使用γ=ρ×δ來獲取，其中，γi值越大，xi越有可能成為聚類中心。將所有點的γ值降序排列，并與坐標平面上繪出。由于聚類中心的γ值較大，而其他點的γ值較小且呈平滑趨勢，故可以使用一條平行于橫線的直線將其分開，使得直線上方的γ值所對應的點即為聚類中心。當聚類中心找出后，將剩余點分配到其高密度最近領所屬的類中。

4 IKDPC算法

4.1 IKDPC算法思想

高維數據的聚類分析存在著很多困難，重點表現在：1）高維數據稀疏性對于信息的識別造成一定的困難；2）隨著維數升高，計算量呈現指數型增長，這導致了對于聚類分析的結果計算更加困難［13］。因此，本文在聚類分析中融入了降維思想，選取已廣泛應用的主成分分析方法，對科技創新人才樣本數據進行降維后再聚類，可以獲得良好的聚類效果。

主成分分析（PCA）是模式識別過程中廣泛應用的特征生成和降低維數的方法，它是在數據信息丟失最少的原則下，對高維變量空間進行降維處理，同時，使得高維數據點的可見性成為可能［14］。本文通過對科技創新人才評價指標體系的樣本數據集進行主成分分析，計算出相關系數指標，得出主成分對原始指標數據的方差貢獻率及累計方差貢獻率，當累計方差貢獻率達到或者超過85%，即m滿足：≥85%，且特征值大于1，從而求出科技創新人才評價指標體系的主成分指標m（m＜p），然后對所求出的m個主成分指標數據進行聚類分析。

為了克服克服傳統DPC算法的缺陷，本文引入相似性系數來調節個點對當前點的密度貢獻權重，提出帶有相似性系數的高斯核函數來計算其局部密度［15］。對于每個樣本數據點xi，其局部密度ρi定義如下：

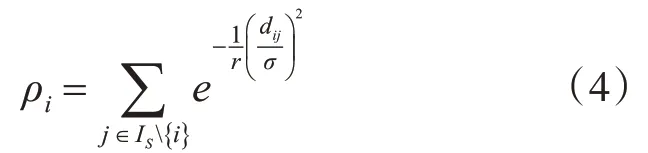
其中，σ取數據量的2%［9］，r為相似性系數，表示密度函數與數據點相似度的關系程度，該值越大，距離點xi越近的點對其密度ρi的貢獻權重越大。樣本數據點xi的距離δi計算方式與DPC算法相同。對于聚類中心的選取，考慮到ρ和δ值可能處于不同的數量級，因此，對兩者進行歸一化處理以有效獲得聚類中心γi，γi定義如下：

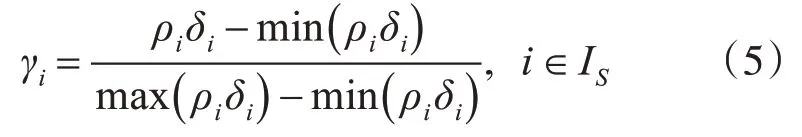
利用式（4）、式（2）計算出個點的ρ和δ值，式（5）計算出相應的γi值，然后通過γ值決策圖選取較大的前M個γ值對應的點獲得聚類中心。

由于聚類中心往往出現在高密度區域，故將各聚類中心某鄰域內的點看作核心點，而將其他點看作非核心點。核心點的獲取方法為先將剩余點分配到距其最近的聚類中心所在的類中，然后計算各局部類Cm中所有點與其類中心cenm間的平均距離um，若xi以下式（7），即xi∈Cm在cenm的θum鄰域內，則xi為核心點。

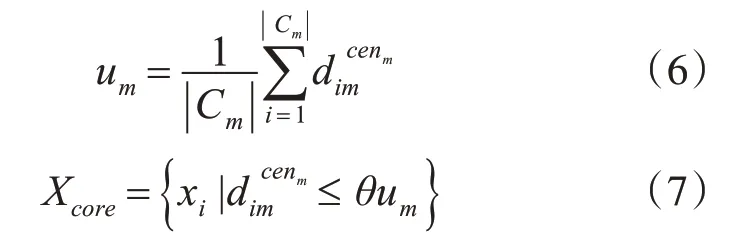
其中，|Cm|為第m個局部類Cm中的所有數據點的數目，為點xi∈Cm與cenm間的距離；θ與數據集大小N有關，取N‰；Xcore為核心點集合。

對于剩余各點，本文設計了兩種全新的分配策略，策略一是以核心點集合Xcore中每個點為中心，不斷地搜索未分配的KNN并將之分配到該點所在的局部類中。策略二則是根據式（8）計算xi和xj的相似度sij，表示兩點距離大小，距離越近，sij越高。每個點的歸屬由其KNN分布決定，若xi的KNN中屬于Cm的點越多且與xi的距離越近，則sij值越大，此時xi被分配到到Cm的概率Pim也越大。的計算如式（9）：

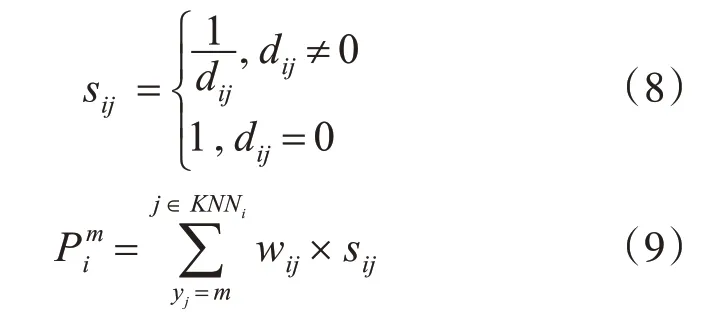
綜上所述，本文提出的IKDPC算法首先在聚類分析中融入了主成分分析法對高維數據進行降維處理，進而在傳統DPC算法中引入相似性系數來調節樣本數據點的密度貢獻權重以計算其局部密度，最后設計了全新的兩種樣本數據點的分配策略，有效提高了數據的聚類效率和聚類質量。

4.2 具體算法步驟

IKDPC算法步驟如下。

輸入：數據集S，樣本近鄰數K，相似性系數r。

輸出：聚類結果。

Step1：對樣本評價指標數據集S使用主成分分析方法，選取前m個主成分指標，該選取滿足累計貢獻率在[8 5%,100%]區間；

Step2：對選取的m個主成分指標新數據集應用改進的DPC算法進行聚類；

Step2.1：計算新數據集中各個數據點間的歐式距離dij，根據式（4）和式（2）計算每個數據點的ρ和δ值；

Step2.2：通過對計算的ρ和δ進行歸一化處理，得到γ，進而構建決策圖獲得聚類中心；

Step3：使用式（6）和式（7）提取核心點，并采用策略一將待分類點歸類：

Step3.1：將核心點集合Xcore至于隊列Q；

Step3.2：取隊列頭xa，將其從Q刪除，然后查找其K個最近鄰KNNa；

Step3.3：若x′∈KNNa未被分配，Step4則將x′分配到xa所在的類中，并將x′添加至Q尾；否則轉Step3.2；

Step3.4：若Q=?，終止該策略；

Step4：根據策略二分配剩余k個點：

Step4.1：依式（8）和式（9）計算每個點的Pim(i=1,2,…,k)，

將該結果存入矩陣Pk×M，同時將的值以及類別號m分別存至向量MP和MI；

Step4.2：若MP中有非零值，則將值最大點xo歸入MI(0)所表示的類中，轉到Step4.3，否則終止該策略；

Step4.3：更新P、MP、MI，令MI(0)=0。對于未分配的點xp∈KNNo，更新P[p][m]、MP(p)、MI(p)。

Step4.4：若MP中所有元素均為0，則終止；否則轉Step4.3；

Step5：若仍然沒有被處理的點可以看作噪聲點，將其歸入到最近鄰所在的類中去。

5 實證研究

5.1 數據收集及整理

本文通過閱讀相關研究文獻、人物傳記提取杰出科技創新人才的評價指標，然后設計發放科技創新人才評價調研問卷，整個過程符合調查抽樣隨機性的原則，問卷發放的對象主要是科研院所及高校人員，調研的結果能反映科技創新人才素質的真實情況。最后將調研問卷的結果進行整理打分，以科技創新人才評價指標體系中的24個評價指標反映出樣本人員所對應的指標得分（分數越高代表對應的素質越高，每個指標的滿分為5分）。經過去噪、去除不合理樣本等預處理，最終共收集科技創新人才有效樣本指標數據352例，科技創新人才樣本指標數據如下表2。

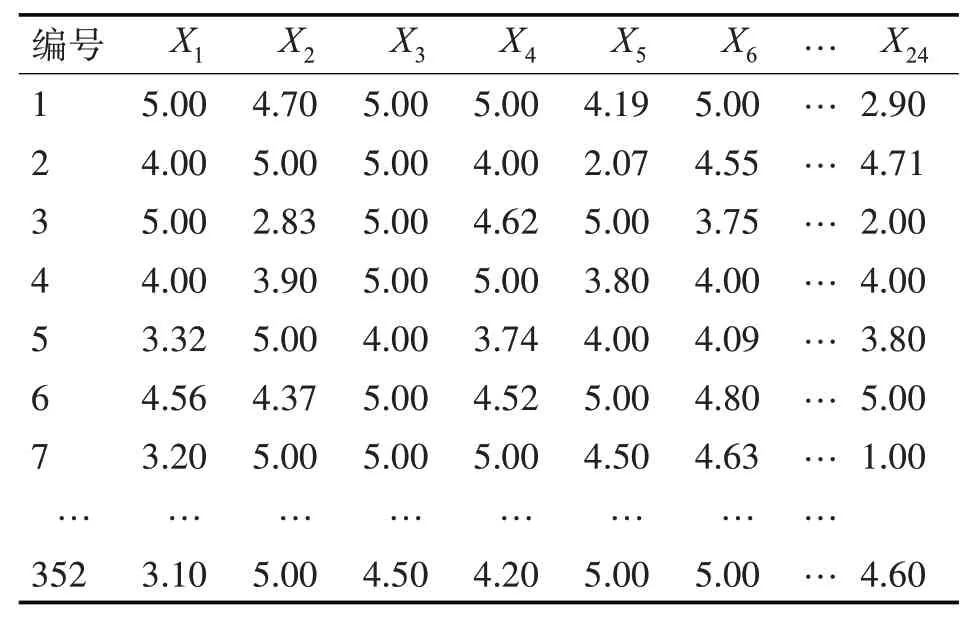
表2 科技創新人才評價指標數據

5.2 實證結果分析

首先把整理好的352例科技創新人才的24項評價指標數據導入SPSS中進行主成分分析，結果見表3。

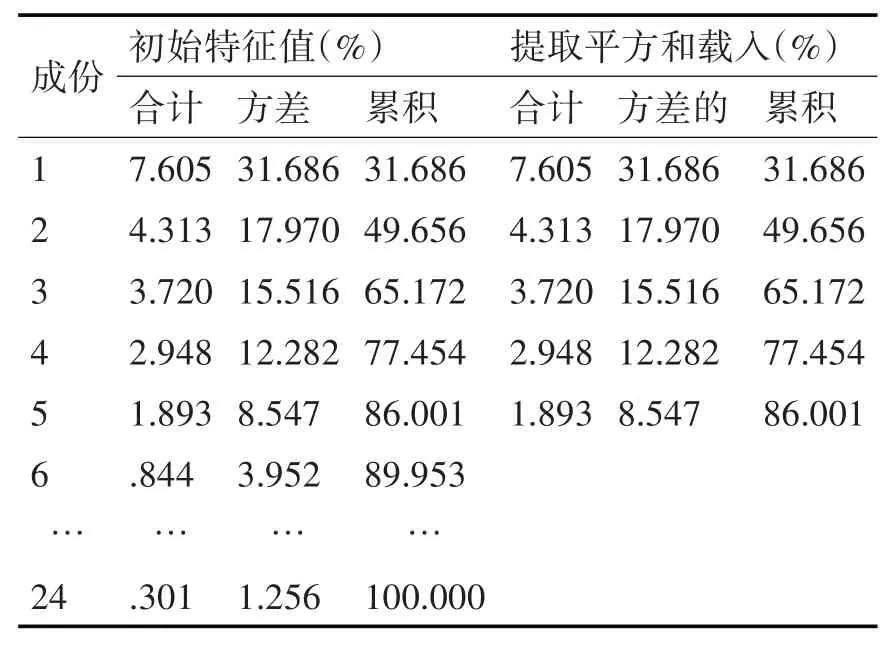
表3 主成分分析解釋總差異

從表3中可以看出，第一成分到第五成分特征值都大于1，并且累計方差貢獻率達到86.001%，可知這5個成分包含原始24個成分信息量的86.001%，可以反映原始數據的主要信息。因此，本文提取前5個成分作為主成分指標進行接下來的聚類分析。聚類結果以表4展示如下。

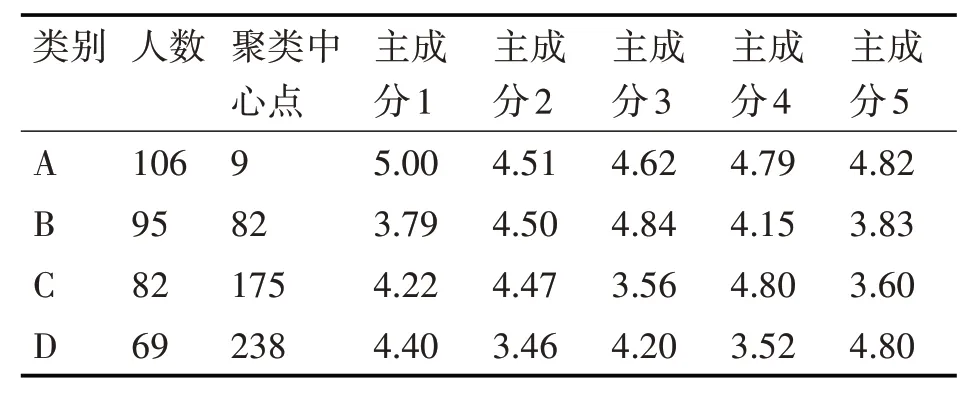
表4 科技創新人才主成分指標聚類結果

根據表4可以看出A類樣本人數為106人，聚類中心點為9號樣本點，分析其主成分指標得分情況可知此樣本人員各個主成分指標分數都較高，因此A類樣本代表的是綜合全面型的科技創新人才；B類樣本人數為95人，聚類中心點為82號樣本點，分析其主成分指標得分情況可知此樣本人員主成分2和3分數顯著，即他的受教育程度較高且知識運用能力強，因此B類樣本代表的是具有良好教育背景的知識應用型科技創新人才；C類樣本人數為82人，聚類中心點為175號樣本點，分析其主成分指標得分情況可知此樣本人員主成分4分數顯著，即他擁有豐富的知識存儲量，因此C類樣本代表的是擁有知識積累型的科技創新人才；D類樣本人數為69人，聚類中心點為175號樣本點，分析其主成分指標得分情況可知此樣本人員主成分5分數顯著，即他具有較強的想象力，因此D類樣本代表的是創新思維型的科技創新人才。結合以上分析可知本文算法能夠得到較好的科技創新人才分類結果。

5.3 算法實例分析

為了驗證數據降維對聚類效果的提升，分別將DPC算法和IKDPC算法在1～24個科技創新人才評價指標成分張成的數據集中進行聚類，使用分錯率（CER）、ERRORRATE和調整Rand系數（Adjusted Rand Index，ARI）三個指標綜合衡量聚類效果，結果如表5所示，科技創新人才在降維過程中維數超過5時各項指標都產生了大幅度變化，各個指標均不理想。

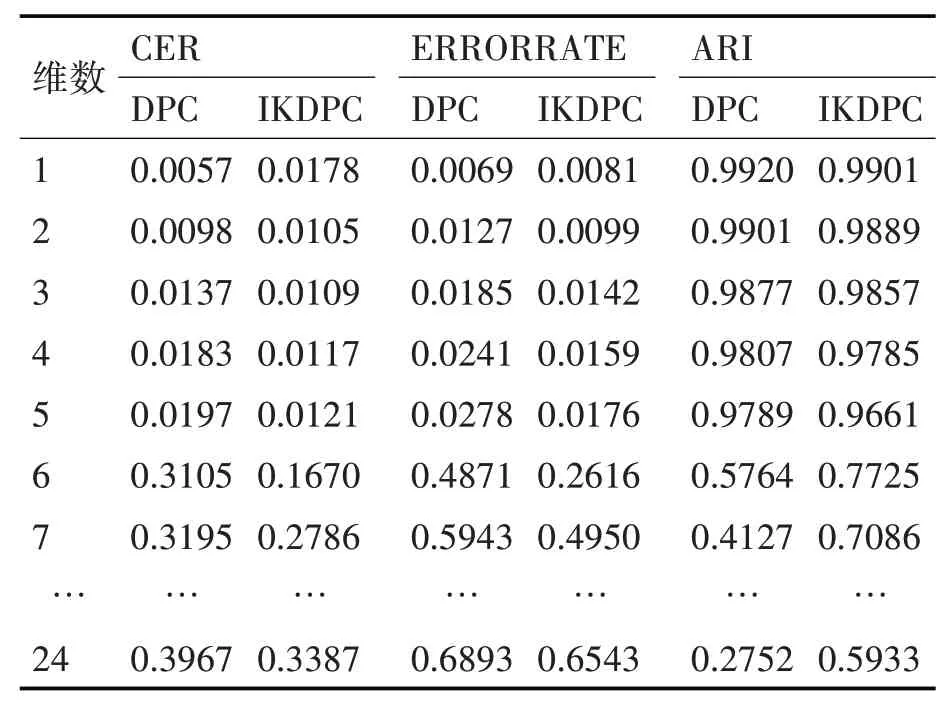
表5 DPC和IKDPC的樣本指標數據聚類對比

最后，為了對比本文提出的IKDPC算法的有效性，本文將聚類算法研究中廣為采用的聚類精度（Clustering Accuracy，ACC）、調整互信息系數（Adjusted Mutual Information，AMI）、ARI這三個指標作為聚類算法性能度量評價標準［16～17］。其中，ACC與AMI的取值范圍均為[0,1]，ARI的 取值范圍為[- 1,1]，各指標值越大，越表示聚類質量越高。本論文算法與其他算法對樣本數據進行驗證，三個指標的比較結果見表6。

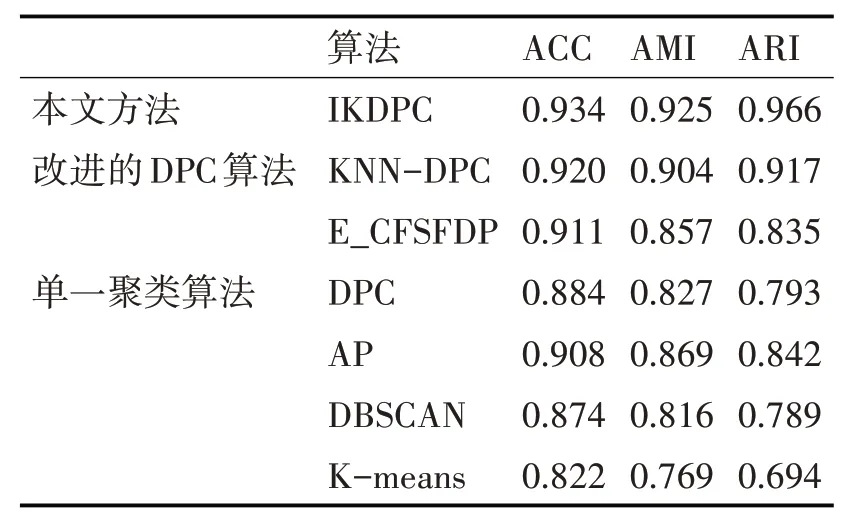
表6 各算法有效性比較

綜上所述，本文算法能夠克服高維數據對聚類過程的不利影響，聚類結果區分性強且聚類有效性高，能夠應用于科技創新人才的實際分類問題。

6 結語

本文針對科技創新人才分類問題，運用定性與定量相結合的方法，先通過資料收集和調研問卷的方式整理制定出相關科技創新人才的評價指標體系，然后提出IKDPC算法對樣本指標進行聚類分析，與傳統聚類方法相比，該方法能夠對高維數據降維，提取指標維數中的主成分指標，并且給出了新的適用于任意數據集的局部密度計算方法，以及兩種不同的剩余點分配策略。采用本文方法對科技創新人員進行聚類分析，充分挖掘聚類信息，客觀合理地將科技創新人才進行分類，對不同類別的科技創新人才制定不同的培養計劃，能夠為科技創新人才培養過程中的分類提供科學化的決策支持。本文方法具有一定的通用性，也可以用于其他類似人員的分類問題，例如醫學人才分類、軍事人才分類等。