一種代價敏感的旋轉森林分類算法*

周爾昊 高 尚

（江蘇科技大學 鎮江 212001）

1 引言

近年來，分類器集成思想成為機器學習領域研究的一大熱點。其中的Bagging［1］和AdaBoost［2］算法是該領域具有代表性的集成策略。文獻［3］指出提高集成分類器的分類效果的方法基本從兩方面展開：一是提高基分類器之間的差異性，二是提高各個基分類器的分類精度。如文獻［4］中的ROFCO算法通過向訓練集中加入差異性數據來減少基分類之間的相關性；再如文獻［5］中以多層感知機作為Bagging的基分類器，提高了基分類器分類精度，以得到更好的分類結果。目前，以各種決策樹（ID3、C4.5、CART）等作為基分類器的集成算法因其在分類問題上的良好表現，越來越受到集成研究者的重視。Rodriguez［6］等于2006年提出的一種新的集成算法——旋轉森林（ROF）算法，該算法以決策樹作為基分類器，通過特征變換增大基分類器之間的差異性，以獲得更好的集成效果。

隨著研究的深入，集成學習越來越多的被應用于解決不平衡問題。不平衡數據分類問題是機器學習領域一大難題，日常生活中會在很多行業面臨此問題，比較常見的如電通行業中的欠費預測、醫療行業中的病情診斷等［7］。然而，目前大多數機器學習分類算法并不能很好解決不平衡數據分類問題。代價敏感集成學習是一種不平衡數據分類方法，主要有三種實現方式，分別是：1）從學習模型出發，針對算法本身的改進；2）從貝葉斯風險理論出發；3）從預處理角度出發，將代價用于權重的調整，如AdaCost算法。

本文提出了一種代價敏感的旋轉森林算法（CROF），首先通過旋轉森林算法實現數據的預處理，然后以CART分類樹作為基分類器，在訓練基分類器過程中引入誤分類代價，改變CART分類樹屬性分裂原則，得到代價敏感的CART分類樹，最后采用置信度這一指標來確定樣本的最終類別。該方法不僅通過旋轉森林算法減少了基分類器之間的相關性，還通過引入誤分類代價提升了基分類器對于不平衡數據的分類能力。通過實驗對比分析，該方法能夠有效處理不平衡數據分類問題。

2 相關技術

2.1 代價敏感學習

代價敏感學習（CSL）最初來源于醫療診斷問題［8］。在醫療診斷過程中，將一位患者診斷為健康所付出的代價遠大于將一位健康的人診斷為患者。在機器學習中，CSL指為不同類別賦予不同的權重，在訓練過程中使機器更加“重視”那些擁有更高權重的類別，從而獲得理想的模型。這一思想更多地被運用來解決不平衡數據分類問題，因為類別的分布不平衡，分類算法往往過度訓練多數類而犧牲了少數類的分類精度。由于CSL是以最小化分類代價為目標的［9］，所以通過賦予少數類更高的分類錯誤代價，使機器在分類過程中大大提高了模型對于少數類的分類精度，從而有效解決了不平衡數據的分類問題。可以用代價矩陣表示分類器錯分時付出的代價［10］，設CL為少數類，CM為多數類。代價矩陣如表1所示。

表1 代價矩陣

其中，C（i，j）表示將j錯分為i的代價。

代價矩陣確定后，用貝葉斯構建風險函數，類別x被劃分為類別i的最小期望代價：

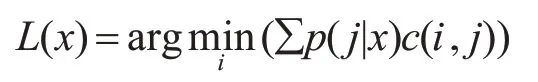
其中：p(j|x)表示把樣本x劃分為j類的后驗概率。

2.2 旋轉森林

旋轉森林（Rotation Forest）［11～14］于2006年 提出。該算法的核心是特征變換思想。先將屬性劃分為大小相等的K個不重疊子集，然后通過PCA、旋轉矩陣等變換方法獲得新的樣本數據。由此得到的各子樣本數據相互有所區別，從而提高了各基分類器的差異性和準確性。

現設定F表示屬性集，D1，D2，…DL表示L個基分類器，用N×n的矩陣X表示有N條數據記錄的訓練樣本集，n表示樣本特征數。模型構建步驟如下。

1）將F隨機劃分為大小相等的K個子集，則每個子集約有M=n/K個屬性。

2）用Fij表示訓練第i個分類器Di所使用的訓練集的第j個子屬性集，對訓練集進行75%重采樣，產生一個樣本子集X’ij，通過主成分分析（PCA）對Fij中的子屬性進行特征變換，得到Mj個主成分：，。

3）重復步驟2），得到K個子屬性集，將其主成分系數存入系數矩陣Ri：

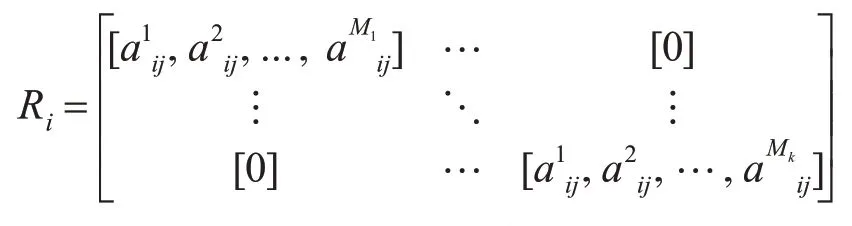
根據原始屬性集排列順序重新旋轉矩陣Ri得，然后通過XRi’操作得到分類器Ci的訓練集，在此訓練集上訓練基分類器Di，重復以上步驟L次得到L個基分類器。這里基分類器采用決策樹類型算法，因為其對特征的旋轉較敏感，得到的各個分類器有更大的差異性。

4）最終分類結果以最大置信度來決定，對于一個樣本x，用di,j(xR'C)表示用分類器Di預測x屬于c類可能性，label表示所有可能的類別，則x屬于c類的置信度為

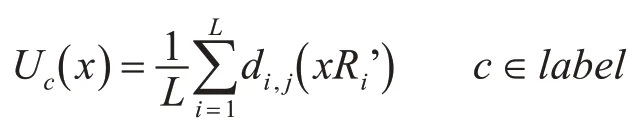
由此可以通過式（3）判定x的最終類別：

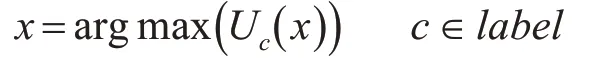
3 代價敏感旋轉森林算法

傳統隨機森林算法在特征子空間構造決策樹，降低了數據維度，本身適合處理高維數據，若向其中引入代價因子，可以同時處理高維不平衡數據［15］。但其在有噪音或樹數量設定不當的情況下存在過擬合問題。相比于傳統隨機森林算法，旋轉森林算法通過特征變換得到的各基分類器的差異性和準確性都變大，在降低數據維度的同時也可以較好地避開過擬合問題，在此基礎上向基分類器引入代價因子得到代價敏感旋轉森林，相比于傳統的代價敏感方法以及現有的與隨機森林相結合的代價敏感方法，代價敏感旋轉森林算法可以更好地處理高維不平衡數據。

3.1 代價構造

本文采用的代價敏感學習方法從學習模型出發，主要對決策樹算法進行改進，從分裂標準的選擇方面引入代價矩陣，使之能在不平衡數據集上有良好表現。

代價敏感旋轉森林算法的基分類器采用CART決策樹算法。在旋轉森林算法得到的新的訓練樣本上構造不剪枝的CART分類樹。CART決策樹的每個節點可選的分裂屬性為一固定數量M，且M≤F，F為樣本所有的特征數目，每次分裂從F中有放回的取M個屬性計算最佳分裂屬性。CART分類樹采用Gini指數來選擇劃分屬性及劃分點。Gini指數是一種不等性度量，又叫做“不純度”指標，表示一個隨機選中的樣本在子集中被分錯的可能性。也就是說，當一個節點中所有樣本都是一個類時，指數不純度為零；而當節點類別分布均與時，指數應該很大。Gini指數的定義如下：

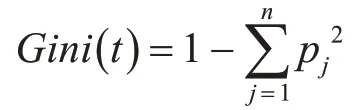
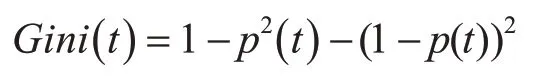
其中p（t）表示節點t處少數類個體比例，1-p（t）表示多數類個體比例。

在CATR分類樹屬性分裂過程中，算法選擇下一個分裂節點的原則是使不純度下降最快的屬性，即使Gini指數變化量最大的屬性，其計算公式如下：

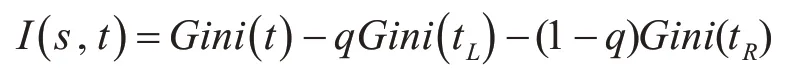
其中：q代表左邊節點的實例比例，1-q代表右邊節點的實例比例。現在向Gini指數計算中引入誤分類代價因子：

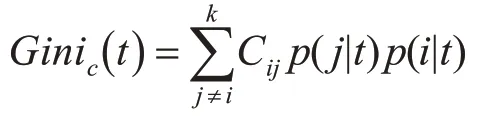
其中：Cij代表誤分類代價，為一固定數值，根據研究樣本實際分布決定。中分子，Π(j)為類別j的先驗值。分母。此時，不純度下降落差更新為

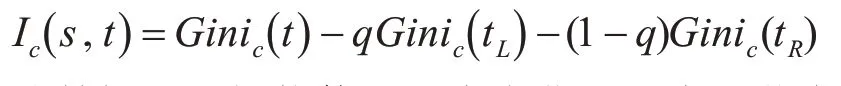
同樣地，選擇能使不純度變化量最大的節點作為最佳分裂屬性。

通過以上操作，成功的將懲罰代價Cij引入到了CART算法中，經過修改的CART算法在每一次選擇新的屬性進行分裂時都考慮到了實際樣本的不平衡性，由此得到的CART分類樹能夠更好地處理不平衡數據集。

3.2 算法步驟

1）根據實際樣本多數類與少數類比例計算誤法類代價C（CL，CM），C（CM，CL）；

2）運用旋轉森林算法處理原始訓練樣本集，得到D1，D2，…，DL個用于訓練基分類器的新的數據集；

3）在D1上建立不剪枝的CART決策樹，引入誤分類代價，修改CART決策樹的屬性分裂計算方法；

4）重復步驟3），直到得到L個構造完成的基分類器；

5）以最大置信度為標準輸出樣本的最終類別。

4 實驗及分析

4.1 實驗數據集、評價標準與參數設置

為驗證算法有效性，從UCI中選擇了五組數據集，由于CROF算法著重解決二分類的不平衡數據問題，故通過調整類別數使這五組數據呈現出二分類上的不平衡性。修改過后的數據集如表2所示。

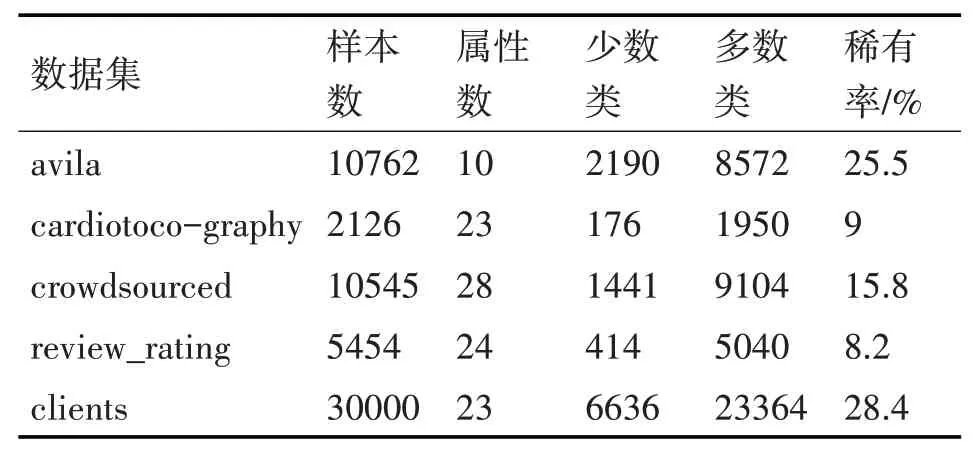
表2 修改后的數據集

通常通過混合矩陣來衡量分類算法的性能，如表3所示。

表3 二分類混淆矩陣

本次實驗中，選取AUC值、真正例率（TPR）、f-度量（f-measure）來衡量算法性能。AUC值是一個比精度好得多的指標，它可以反映多數類及少數類的平均分類情況，對于不平衡類別的分類問題，使用AUC進行模型評估通常比使用精度更有意義。TPR度量的是少數類樣本中有多少被預測為少數類；f-measure是準確率（PPV）和真正例率（TPR）的調和平均，由于同時考慮了準確率和真正例率，所以它對于不平衡的二分類數據集來說是一種較好的度量。

對于誤分類代價Cij設置則根據所選取數據集實際情況而定，如clients數據集中，多數類與少數類比例為3.5，設CL為少數類，CM為多數類，若C（CL，CM）設為1，則C（CM，CL）應設為3.5，以此體現若誤分少數類將帶來更大的懲罰。

4.2 實驗結果與分析

將CROF算法分別于CART決策樹算法、RF（隨機森林算法）、ROF（旋轉森林算法）進行比較。四種算法的AUC值如圖1所示。

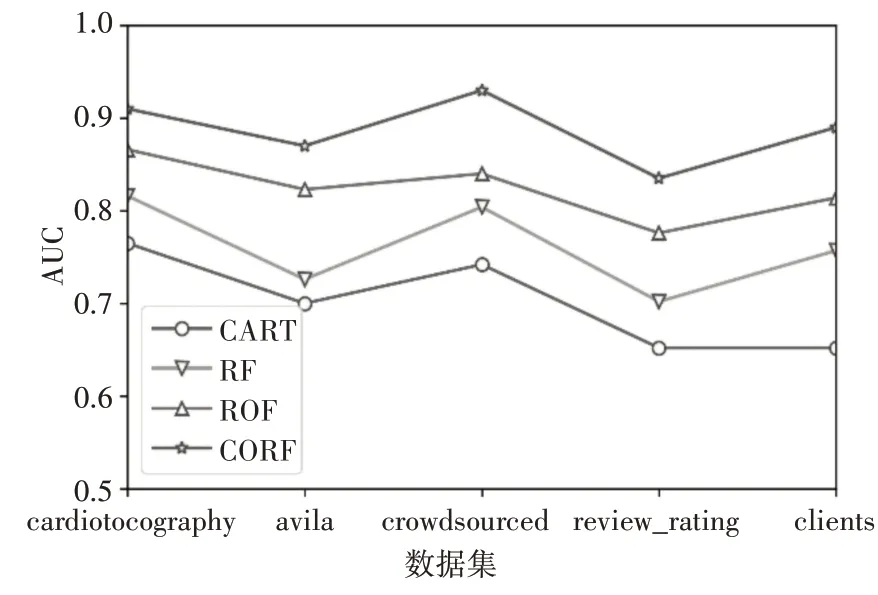
圖1 CATR，RF，ROF，CROF的AUC值比較

從圖1中可以看出，以集成為基礎的RF算法相較于普通的CART決策樹算法可以一定程度上緩解過擬合問題，但其對于少數類的分類不敏感，AUC值表現一般。ROF算法通過特征變換，在避開過擬合的同時其分類器的準確性有所提升，對比RF算法AUC值有了提升。而CROF算法在此之上通過引入代價因子，能夠處理高維不平衡數據，其AUC值比之ROF算法又有了進一步提升。這說明CROF算法對多數類及少數類的分類均有良好表現。

由于算法著重于解決不平衡數據的分類問題，所以對于少數類的分類精度有著更高的要求。表4、表5分別是四種算法在各數據集上的TPR和f-measure的平均值，圖2、圖3則是對表格數據的直觀反映。

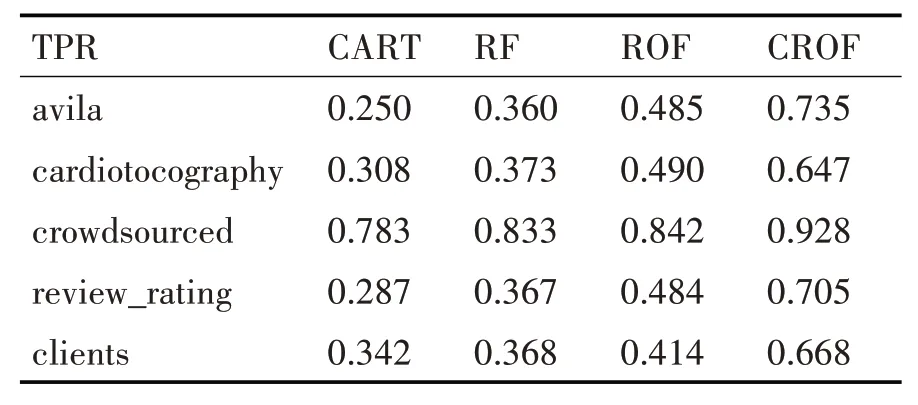
表4 四種算法下各數據集的TPR值

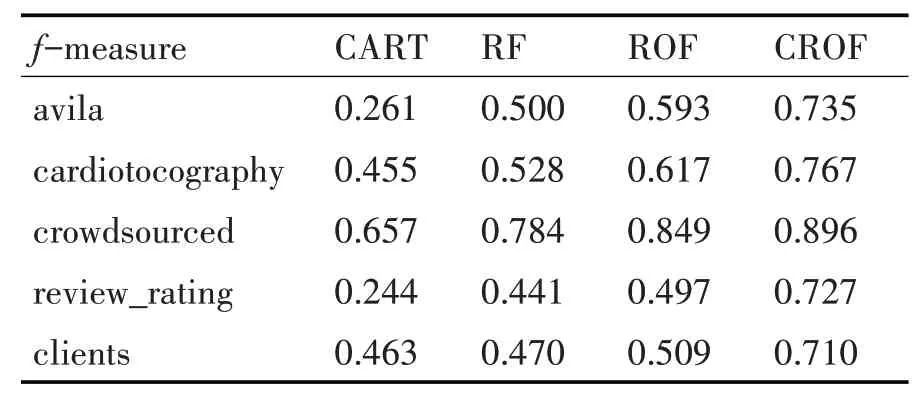
表5 四種算法下各數據集的f-measure值

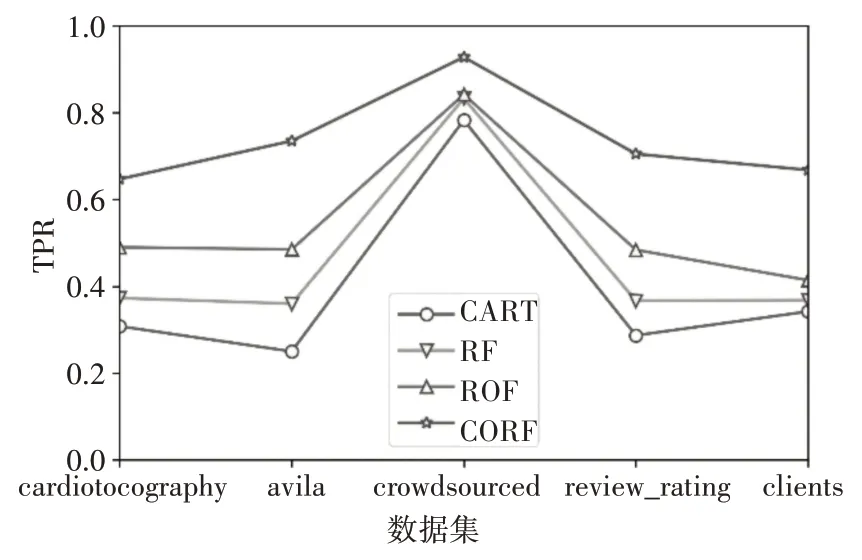
圖2 各數據集下四種算法TPR比較

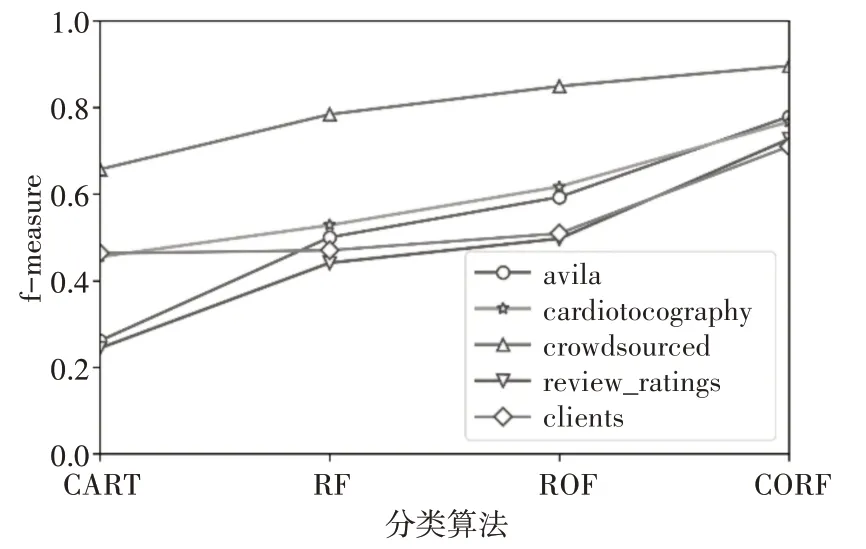
圖3 四種算法下各數據集f-measure比較

從圖表中可以看出，CROF算法對于數據集中少數類的分類精度優于其他三種算法，在AUC值較其他方法略有提升的基礎上，CROF算法對于少數類的分類準確率有較大提升。以上實驗說明CROF算法可以更好地處理不平衡數據。

5 結語

傳統算法處理不平衡問題時往往基于類別平衡的假設，當應用于不平衡數據時性能并不理想［16］。CROF算法利用集成思想，通過ROF模型實現了數據的預處理，向CART算法中引入誤分類代價，改變了CART屬性分裂計算規則，使得分類器不僅多樣性與準確性均得到改進，而且能有效處理不平衡數據問題，進而提高集成后的分類器分類性能。提出的CROF算法與傳統算法相比有更好的AUC、TPR及f-measure值。說明該算法在不平衡問題上是有效的。