基于勢均衡多伯努利濾波的SLAM方法*

李寧 章飛

（江蘇科技大學 鎮江 212003）

1 引言

同是定位與地圖創建（Simultaneous Localization And Mapping，SLAM）方法可以描述為移動機器人在未知環境中，從一個未知的位置出發，通過攜帶傳感器獲取自身周圍的環境信息，逐步構建環境地圖，再根據環境地圖實現機器人自身定位［1～2］。不同于許多經典的陸上傳統導航方法，SLAM方法不需要機器人獲取準確的先驗環境信息，成為水下機器人自主導航領域的一個研究熱點［3］。

由于水下環境復雜，雜波密集，導致傳統SLAM算法的數據關聯精度降低，計算復雜度大大提高，從而使得濾波算法的精度大幅度降低。Mahler提出了一種基于隨機有限集（Random Finite Set，RFS）的多目標貝葉斯（Multi-target Bayesian filter，MTB）濾波器［4］，該濾波方法通過對測量更新中的所有可能關聯求平均來規避數據關聯問題。RFS是集值隨機變量，即狀態向量的數量以及狀態向量本身是隨機的。因此，RFS自然地捕獲了地圖的不確定性。在后續的研究中，Mahler根據這個理論先后提出了概率假設密度（PHD）［4］、勢概率假設密度（CPHD）［5］、多目標多伯努利（MeMBer）［6］等濾波方法。Mullane J等首次將RFS理論應用到SLAM領域［7～9］，提出了基于Rao-Blackwellised粒子濾波器的PHD-SLAM算法，并給出了該算法高斯混合的實現。

PHD-SLAM算法在線性條件采用高斯混合實現，在非線性條件下采用序貫蒙特卡洛實現［10～11］，但這兩種實現方法都采用了近似的策略來計算粒子權重，雖然避免了數據關聯，但其算法估計誤差較大。Mahler提出的MeMBer濾波器不同于PHD和CPHD，它是對多目標的后驗概率密度進行估計，而且不用任何近似策略計算粒子權重，因此該算法的精度較高。B.-T.Vo在文獻［12］中指出MeMBer濾波器會過多估計目標數目，針對這個問題，B.-T.Vo修改了多伯努利濾波器更新階段的公式，提出了勢均衡多伯努利（Cardinality Balanced Multi-Bernoulli，CBMBer，CBMBer）濾波器，使得目標數的估計更加準確。在上述方法的啟發下，本文提出了基于勢均衡多伯努利濾波的SLAM方法（Cardinality Balanced Multi-Bernoulli SLAM，CBMBer-SLAM）。該方法不用進行數據關聯，也不需要用近似策略進行粒子權重計算，降低了算法計算復雜度，并提高了濾波算法的精度，采用無偏差的勢估計避免了過多估計地圖特征數目的問題，提高了地圖特征估計精度。

2 SLAM的隨機有限集模型

2.1 特征地圖的RFS模型

在基于RFS的SLAM算法中，k時刻環境的特征地圖用一個隨機集合Mk表示，其RFS模型為

其中：Mk-1=M∩FoV(X0:k-1)，表示0到k-1時刻地圖特征的RFS，M為整個地圖特征的RFS；Xk表示k時刻機器人的位姿，表示k時刻新生地圖特征。地圖特征數目在機器人運動過程中單調增加。

2.2 觀測的RFS模型

在實際情況中，針對地圖特征觀測的無序性，用集合Zk表示k時刻機器人的特征觀測集合，此時機器人位姿為Xk，其RFS模型為

其中，Dk(m,Xk)表示機器人在m處路標特征產生的測量RFS，其模型為一個伯努利型RFS。Dk(m,Xk)={z}的概率密度為P（Dm|Xk)gk(z|m,Xk)，P（Dm|Xk)表示當機器人位姿為Xk時，能夠檢測到位于m處的地圖特征概率，即檢測概率；gk(z|m,Xk)表示機器人的觀測模型。Ck(Xk)表示機器人位姿為Xk時由環境雜波產生的量測RFS。

2.3 RFS框架下的SLAM問題描述

在RFS-SLAM中，使用RFS表示地圖特征Mk及觀測信息Zk，其中，Zk=表示地圖的地標，zki表示時間k的特征量測。集合表示不像向量表示那樣（例如FastSLAM）假設地標或量測是順序存在的，因此可以避免地圖特征關聯導致的算法復雜問題。在RFS框架下，SLAM問題可以轉化成Zk條件下，對Mk和X1:k聯合后驗概率密度的估計過程。其表示形式為

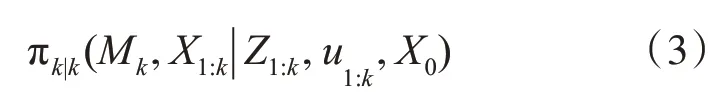
由于水下環境的制約，機器人在SLAM過程中自身的真實位姿無法得知，因此無法直接對Mk和X1:k的聯合后驗概率密度進行直接估計，只能利用條件概率公式，將聯合后驗估計分解成兩個部分進行，這兩個部分分別為機器人位姿估計及機器人位姿估計下的地圖特征估計，分解后的聯合后驗估計的表示形式為

3 CBMBer-SLAM算法

CBMBer-SLAM方法可分為兩個部分：一是對機器人的位姿進行估計；二是在粒子位姿采樣估計的基礎上進行地圖特征后驗概率密度估計。本文算法在機器人位姿估計部分采用的是Rao-Blackwellised粒子濾波器，濾波過程中，機器人軌跡的可能路徑由各個粒子進行描述。在粒子位姿的基礎上，采用CBMBer-SLAM濾波器進行地圖特征后驗概率密度估計，利用高斯混合實現方式。算法在遞歸的過程中傳遞的是多伯努利RFS參數，即多伯努利元素的概率密度函數和各元素的存在概率。最后利用地圖特征的數目和位置更新結果來進行粒子的重要性采樣，運用粒子加權平均來更新機器人的位姿。

在CBMBer-SLAM濾波器中，地圖特征的后驗概率密度被認為是一個多目標狀態，由多伯努利RFS表示。多伯努利RFS是多個相互獨立的伯努利RFS的聯合，其表示形式可以簡記為π=，r表示存在概率，p表示概率密度，L表示多伯努利項目數。在k-1時刻，CBMBer-SLAM的強度函數為

采用高斯混合實現CBMBer-SLAM地圖估計時，要滿足以下三個條件：

1）每個粒子都服從線性高斯的運動模型和觀測模型為

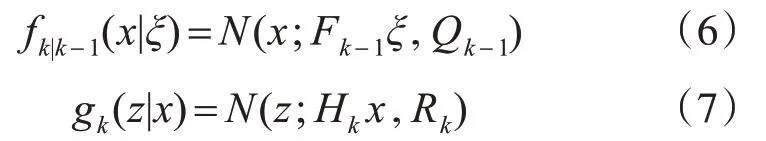
fk|k-1(x|ξ)表示k時刻的狀態轉移函數，gk(z|x)表示K時刻地圖特征的擬然函數；N(·;m,P)表示高斯分布，其中m表示高斯均值，P表示高斯協方差矩陣；Fk-1、Qk-1分別表示狀態轉移矩陣和過程噪聲協方差矩陣；Hk、Rk分別表示觀測矩陣和測量噪聲的協方差矩陣。

2）目標的檢測概率、存活概率與狀態無關

目標的檢測概率為pD,k(x)=pD,k，存活概率為pS,k(x)=pS,k。

3）新生地圖特征也為一個多伯努利RFS。

3.1 勢均衡多伯努利地圖估計

采用GM-CBMBer實現對地圖的估計時，地圖的特征數目和位置由后驗概率密度進行描述，在機器人位姿已知的情況下，每個粒子都對應一個機器人的可能路徑，地圖估計需要對每個可能的機器人路徑進行CBMBer預測和更新。

1）預測

假設k-1時刻，機器人的第i個位姿采樣粒子為，則多伯努利參數集為，該單個粒子在地圖條件下對應的概率密度為，其高斯混合形式為

在k時刻，新生地圖特征的多伯努利概率密度參數集為，在位姿粒子條件下，其中概率密度的高斯混合表達形式如下

預測的多伯努利概率密度參數集為新生特征的多伯努利概率密度參數集并上k-1時刻的后驗概率密度參數集，則預測的多伯努利RFS參數集為

其中：

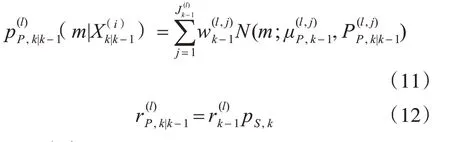
上式中：

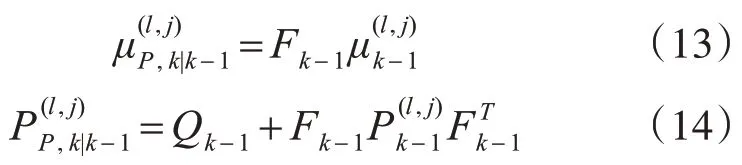
2）更新

由于多伯努利RFS的并集仍然為一個多伯努利RFS，因此在k時刻，預測的多伯努利概率密度參數集記為，式中Lk|k-1=Lk-1+Lb,k。此時，單個粒子概率密度的高斯混合表達示形式為

更新后的地圖特征密度可由如下的多伯努利隨機集表示：

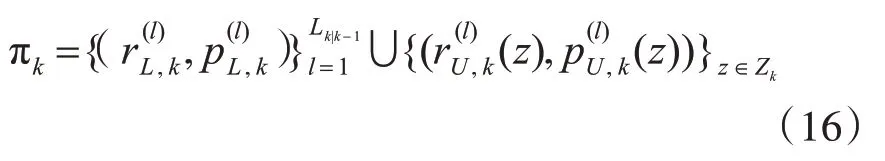
由上式可知，更新后的地圖特征密度由兩部分組成，前半部分表示預測階段的幸存部分，后半部分表示由觀測得到的更新部分。其中：

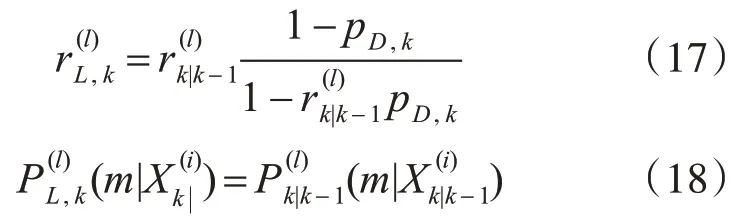
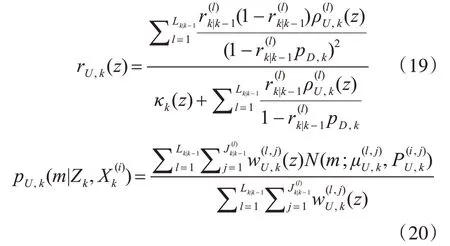
上式中

式（18）、（19）采用了勢均衡多伯努利的更新方式獲得地圖特征的后驗概率密度，該更新方法有效解決了多伯努利濾波帶來的過多估計地圖特征數目的問題，提高了估計精度。

3）高斯項的修剪、合并

隨著新生地圖特征的出現以及更新步驟的增加，表示伯努利項的高斯項目數會不斷增加，這樣就大大增加了計算量，因此我們需要對伯努利項目數以及伯努利項對應的高斯分量進行剪切、合并。首先，設置一個存在概率門限Tr，每一次更新過后，剔除地圖特征存在概率小于門限值的伯努利項。然后，對剔除篩選過后的伯努利項的高斯分量進行剪切、合并，即設定一個權重閾值Tp，將權重小于閾值的高斯分量剪切掉；設定一個高斯分量距離門限Tm，如果剪切過后的高斯分量相互之間的位置距離小于門限Tm，則進行高斯合并。

4）地圖特征提取

地圖特征的估計主要包括對特征點數目的估計和對特征點位置的估計兩方面。設定特征提取門限Tf，高斯項在剪切、合并之后，對權重大于特征提取門限值Tf的高斯分量進行提取，地圖特征的數目即為大于門限Tf的高斯分量數，高斯分量對應高斯項的均值表示地圖特征在地圖中的位置，為提高地圖特征位置估計的精確度，最后用高斯分量的加權平均表示地圖特征的位置。

3.2 機器人位姿估計

本文采用Rao-Blackwellised粒子濾波實現機器人位姿估計。實現過程主要包括粒子重要性采樣和粒子重采樣兩個部分［13～14］。在k時刻，用所有粒子的加權平均和的形式表示機器人位姿的后驗分布。

1）粒子重要性采樣

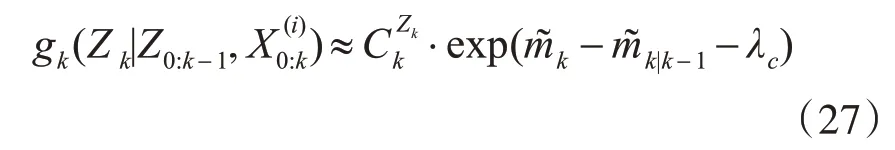
2）粒子重采樣

在粒子重要性采樣結束后需要對粒子進行重采樣，得到新的粒子集。這樣做可以避免粒子退化導致估計精度降低的問題。

4 仿真結果及分析

仿真實驗是在Matlab 2016b版本下進行的，地圖大小為45m*60m，共有25個地圖特征。CBMBer-SLAM仿真結果如圖1所示。

圖1 地圖仿真結果

圖1中，地圖特征的真實位置用“〇”表示，本文算法估計地圖特征的位置用“+”表示，“×”表示地圖環境中的雜波。機器人實際運行軌跡由實線表示，機器人的估計軌跡虛線表示。機器人視域內的雜波服從Poisson分布，機器人傳感器探測特征的概率為PD=0.98。由上圖可知，CBMBer-SLAM地圖構建方面性能優秀。

水下機器人攜帶的傳感器為聲吶傳感器，仿真中噪聲假設為高斯噪聲，運動模型參數具體如表1所示。

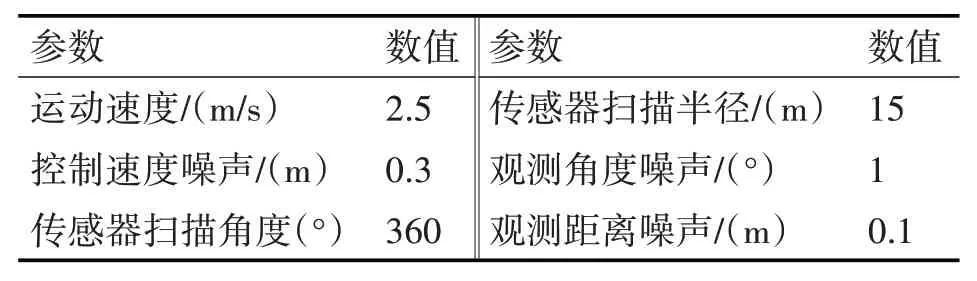
表1 水下機器人運動模型參數

在仿真過程中將本文提出的方法與RB-PHD-SLAM方法的性能進行對比，從機器人定位誤差和機器人地圖特征的估計精度兩個方面驗證本文方法的有效性。

1）機器人定位

用機器人位置均方根誤差（RMSE）作為本文算法和RB-PHD-SLAM算法在機器人定位方面的性能對比指標。在本文仿真實驗中，機器人位姿的采樣粒子數為30個，一共進行10次濾波。通過計算每個時刻機器人位姿的RMSE值來對比兩種方法，仿真結果如圖2所示。

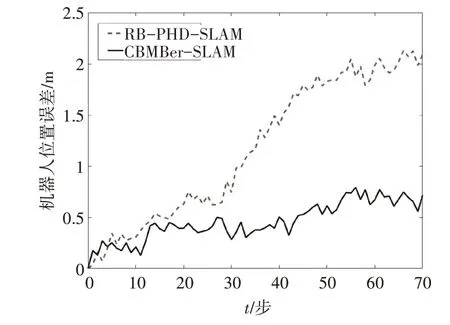
圖2 機器人位置誤差

由圖2機器人位置誤差仿真結果可以對比看出，隨著仿真步數增加，本文方法在相同的條件下機器人位置誤差變化幅度明顯低于RB-PHDSLAM，誤差均保持在1m以下，而RB-PHD-SLAM方法的機器人位置誤差越來越大，說明本文算法在機器人位置估計方面的精度更好。

2）地圖特征估計

本文采用兩種方式對機器人地圖特征估計性能進行評估。一是對每個時刻地圖特征估計的數目與真實地圖特征數目的對比，二是每時刻機器人特征位置估計的誤差對比。仿真結果如圖3、圖4所示。

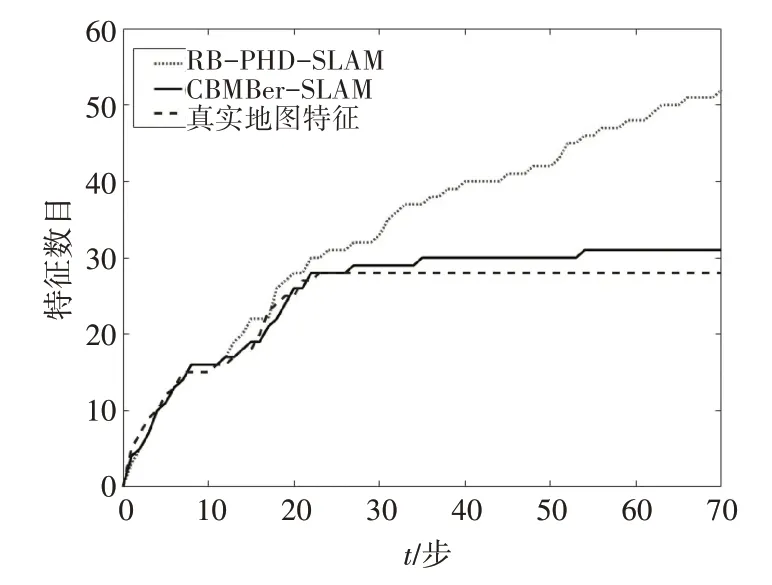
圖3 地圖特征數目對比

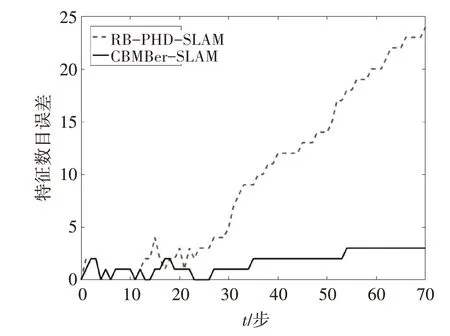
圖4 地圖特征估計數目誤差對比

從圖3可以看出，在前30步兩種算法在特征數目估計上相差不大，都與真實特征數目相接近。在30步之后，由于算法模型誤差以及計算誤差的累積，機器人運動步數逐漸增加的同時，RB-PHDSLAM的地圖特征估計數目開始與真實數目逐漸偏離，估計數目遠遠多于真實特征數目。而本文采用的勢均衡多伯努利濾波的方法，克服了多伯努利濾波過多估計目標數目的缺陷，使得地圖特征數目估計始終與真實地圖特征數目相接近。圖4將兩種方法的特征數目誤差進行對比，可以更加直觀看出兩種算法在地圖特征數目估計方面的優劣，證明了本文算法在地圖特征估計精度方面優于RB-PHD-SLAM方法。

在基于RFS的SLAM方法中，地圖特征信息不像FastSLAM一樣采用有序向量表示，而是采用無序的集合形式表示，導致傳統方法在多目標系統求距離誤差時并不適用，文獻［15］提出的OSPA距離方法是一種用來評價集合之間差異程度的方法，適用于評價本文算法。圖5采用OSPA誤差評價兩種算法的地圖特征位置估計誤差。仿真實驗中，兩種算法各運行10次，取OSPA距離均值。其中OSPA截斷距離取值為2，距離的階數為1階。

圖5 OSPA誤差對比

從圖5可看出，前30步本文方法OSPA誤差與RB-PHD-SLAM方法相差不大，但是30步之后，本文算法的OSPA誤差仍保持穩定，都在1.5m之下；而RB-PHD-SLAM方法的OSPA誤差則隨著機器人運動步數增加而增大，誤差遠遠超過本文方法。對比兩種方法的OSPA可以發現，本文方法的地圖特征估計精度更高而且算法性能方面更加穩定。

5 結語

本文所提的勢均衡多伯努利SLAM算法算法是基于隨機有限集理論的SLAM算法，有效克服了傳統算法數據關聯的問題。在遞歸的過程中，該算法是對多目標的后驗概率密度進行估計，而不用任何近似策略計算粒子權重，因此該算法的精度較高。將無偏差的勢估計方法運用到多伯努利濾波更新中，有效解決了傳統SLAM算法會過多估計地圖特征數目的缺點，并有效提高了算法的整體估計精度。通過仿真實驗，驗證了本文在位姿估計精度和地圖特征估計精度方面的有效性。