《集合》快樂導學
■王佩其
綱舉才能目張,抓住重點,方可事半功倍,集合學習亦如此。那么,學習集合要抓住哪些重點?
一、集合的基本概念
例1下列各式中,正確的序號是____。(寫出所有正確的序號)
①?={0};②??{0};③?∈{0};④0={0};⑤0∈{0};⑥{1}∈{1,2,3};⑦{1,2}?{1,2,3};⑧{a,b}?{b,a}。
解:?不含任何元素,{0}是以0 為元素的集合,①錯誤。?是任何集合的子集,②正確。?是一個集合,集合與集合之間不能用屬于符號,③錯誤。0 是一個數,不是集合,它與集合之間不能使用等于符號,④錯誤。{0}是以0為元素的集合,則0∈{0},⑤正確。{1}和{1,2,3}都是集合,集合與集合之間不能用屬于符號,⑥錯誤。{1,2}和{1,2,3}都是集合,{1,2}中的元素都在{1,2,3}中,則{1,2}?{1,2,3},⑦正確。{a,b}和{b,a}都是集合,兩個集合中的元素完全相同,則{a,b}?{b,a},⑧正確。答案為②⑤⑦⑧。
方法歸納:研究集合問題時,首先要明確構成集合的元素是什么,即弄清該集合是數集、點集,還是其他集合,然后看集合的構成元素滿足的限制條件是什么,從而準確把握集合的含義。利用集合元素的限制條件求參數的值或確定集合中元素的個數時,要注意檢驗集合中的元素是否滿足互異性。
二、集合間的基本關系
例2已知集合A={x|x2-4=0},B={x|ax=1},若B?A,則實數a的值是( )。
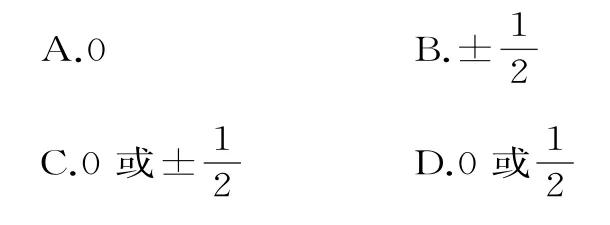
解:易得A={x|x2=4}={2,-2}。由B?A,可對B分情況討論求解。
當B={2}時,由2a=1,可得a=;當B={-2}時,由-2a=1,可得a=-;當B=?時,可得a=0。
綜上可得,a=0或a=±。應選C。
方法歸納:已知兩個集合間的關系求參數的關鍵是將兩個集合間的關系轉化為元素或區間端點間的關系,進而轉化為參數滿足的關系。解決這類問題要合理利用數軸、Venn圖,化抽象為直觀進行求解。用描述法表示集合時應注意集合的代表元素。
三、集合的基本運算
例3設集合M={x∈R|-2 (1)若t=2,求M∩(?RN)。 (2)若M∪(?RN)=R,求實數t的取值范圍。 解:(1)當t=2 時,M={x∈R|-2 (2)若M∪ (?RN)=R,則N?M。 當2-t≥3t+1,即t≤時,N=?,滿足題意;當2-t<3t+1,即t>時,令可得。綜上可得,實數t的取值范圍是。 方法歸納:進行集合運算時,先看集合能否化簡,能化簡的先化簡,再研究其關系并進行運算。離散型數集或抽象集合間的運算,常借助Venn圖求解;連續型數集的運算,常借助數軸求解,運用數軸時要特別注意端點是實心還是空心。

