潛變量增長混合模型在學齡兒童體質指數變化軌跡分析中的應用

大連醫科大學公共衛生學院衛生統計教研室(116044) 雷 芳 宋桂榮 劉啟貴 胡冬梅 李國榮 唐 曉

【提 要】 目的 探討潛變量增長混合模型(latent growth mixture modeling，GMM)和潛類增長模型(latent class growth model，LCGM)在識別兒童體重增長變化潛在類別上的應用。方法 以大連市932名6～12歲學齡兒童的體檢縱向數據為例。運用Mplus8.3軟件構建不同性別兒童體質指數(body mass index，BMI)變化的GMM和LCGM模型。結果 LCGM模型對男女學齡兒童的生長軌跡均識別出3個增長趨勢不同的亞組：“穩定組”、“肥胖組”、“偏瘦組”；GMM模型對男性學齡兒童的生長軌跡識別出2個增長趨勢不同的亞組：“穩定增長組”和“肥胖增長組”。結論 GMM和LCGM模型可以識別學齡兒童BMI發展軌跡的異質性，拓展了描述兒童體重動態變化的方法研究。

兒童生長發育狀況關系到社會發展水平及健康水平。體質指數(body mass index，BMI)，是國際上常用于評價兒童生長發育、營養狀況及胖瘦程度的重要指標[1]。在對BMI多次監測構成的縱向數據的研究中，廣義線性混合模型、多元線性回歸模型等模型是目前常見的分析方法，但這些研究方法都只對調查對象進行了一個群體性BMI軌跡研究，并未對群體內部BMI發展異質性進一步研究與探索。然而，在實際情況中，不同個體BMI變化的軌跡可能是存在差異的，比如，某一兒童群體的BMI隨時間變化可能會呈現“持續保持平穩”、“明顯升高”、“明顯降低”等不同類別的變化軌跡，即研究群體內部可能存在BMI發展趨勢不同的亞群。潛變量增長混合模型(latent growth mixture modeling，GMM)和潛類增長模型(latent class growth model，LCGM)是目前較先進的縱向數據建模方法，可用于識別隨時間變化有不同發展趨勢的群體，探究并確定研究群體中各個亞群的發展趨勢及軌跡特征。本研究通過對大連市學齡兒童縱向數據的分析，來闡述這兩個模型在BMI發展軌跡中的應用。

資料與方法

1.模型原理

傳統的潛變量增長曲線模型(latent growth curve model，LGCM)可采用線性、二次、更高次曲線或分段函數來模擬縱向數據的軌跡，以線性函數為例：

yit=αi+βit+εit

αi=α0+μαi

βi=β0+μβi

其中，yit表示個體i在t時點(年齡)的應變量值，t為測量時點，αi為個體i的截距，即個體指標的初始水平，βi為個體i的斜率，即個體i指標的發展速度。α0和β0分別為群體的平均截距和平均斜率，也稱為固定效應，μαi、μβi分別為個體i的截距和斜率的變異程度，也稱為隨機效應，εit為隨機誤差。此線性模型的潛變量為截距潛變量和斜率潛變量。

GMM模型在LGCM的基礎上增加了分類潛變量，可以將存在異質性的群體分成若干個亞群，描述各個亞群的發展軌跡及其內個體的發展變化的差異，該模型存在兩種潛變量：(1)連續潛變量，包含增長特征參數，即隨機截距、隨機斜率或隨機加速度等因子。(2)分類潛變量：將研究群體分成互斥的亞群來描述群體的異質性[2]。

GMM模型的表達公式如下(以線性函數為例)：

yit=P(C=k)·(αik+βikt+εitk)

αik=α0k+μαik

βik=β0k+μβik

分類潛變量C表示群體可分成的若干個亞群，共包含k個類別；P(C=k)表示個體i屬于第k類的概率；αik和βik分別表示個體i在第k類的截距和斜率，α0k表示第k類的截距均值，用于描述第k類的平均初始值，μαik表示第k類個體間初始值的差異；βik表示第k類的斜率總均值，描述該類的總平均變化率，μβik表示第k類個體間平均變化率的差異。εitk表示個體i在第k類的殘差[3]。

LCGM模型是GMM模型的特例，與GMM模型使用隨機系數來估計個體的斜率和截距不同，LCGM模型假設在同一亞組內個體的斜率和截距均相同，類別組內的發展軌跡不存在個體差異[4]。

LCGM模型的表達公式如下(以線性函數為例)：

yit=P(C=k)·(αik+βikt+εitk)

αik=α0k

βik=β0k

模型擬合優劣的評價指標：(1)模型擬合評價指標有AIC 、BIC、aBIC、Entropy，前三個指標越小說明模型擬合情況越好，Karen等人研究表明，aBIC是最好的信息指標[5]。Entropy評價模型分類的精確性，取值在0～1，一般大于0.8認為該模型的分類精確性較高[6]。(2)模型亞組分類比較包括VLRT和BLRT檢驗，當比較含k類的模型與k-1類模型擬合情況時，若檢驗結果P<0.05，則表示含k個亞類的模型更好，反之，則k-1類模型擬合較好。

2.資料來源

資料來源于2003年至2009年大連市四個區小學的隊列研究數據，數據收集情況見文獻[7]。共有515名男童和417名女童共932名學生納入 6年的隊列研究，資料包含研究對象1到6年級每年的身高(cm)和體重(kg)，BMI=體重/身高2(kg/m2)。按照WHO 2007分性別和年齡別的標準分別計算男童及女童BMI的標準化評分BMI-Z。本研究經大連醫科大學公共衛生學院與倫理委員會批準，所有參與者、家長或法定監護人均已知情同意。

3.模型方法

由于男童和女童的體質存在差異性，且體脂發育不同步，故按性別不同分別進行建模分析[8]。本研究分兩部分進行：將6年監測的BMI-Z作為觀測變量分別擬合線性、二次函數的LCGM和GMM；以前一步得到的最優模型的分類和基線身高作為自變量，以6年身高的總增長值作為因變量進行多元回歸分析，來探討BMI發展趨勢不同的兒童身高增長的差異。

使用Mplus 8.3軟件進行LCGM和GMM模型，使用SPSS 20.0對人口學變量進行統計描述和多元回歸分析。

結 果

1.研究對象基本特征

共有932名學生納入本次研究，其中，男童515名(55.3%)，女童417名(44.7%)，基線的平均年齡為(7.10±0.34)歲；基線的平均BMI：男童(16.31±2.67)kg/m2，女童(15.50±2.16)kg/m2。

2.兒童BMI-Z的LCGM模型擬合結果

LCGM模型擬合男女童的BMI-Z值發展情況的結果見表1和表2。模型結果顯示，男童和女童都是含3個潛在類別的二次函數的LCGM模型擬合情況較好。

表1 LCGM模型擬合統計量結果(男童)

表2 LCGM模型擬合統計量結果(女童)

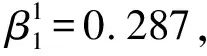
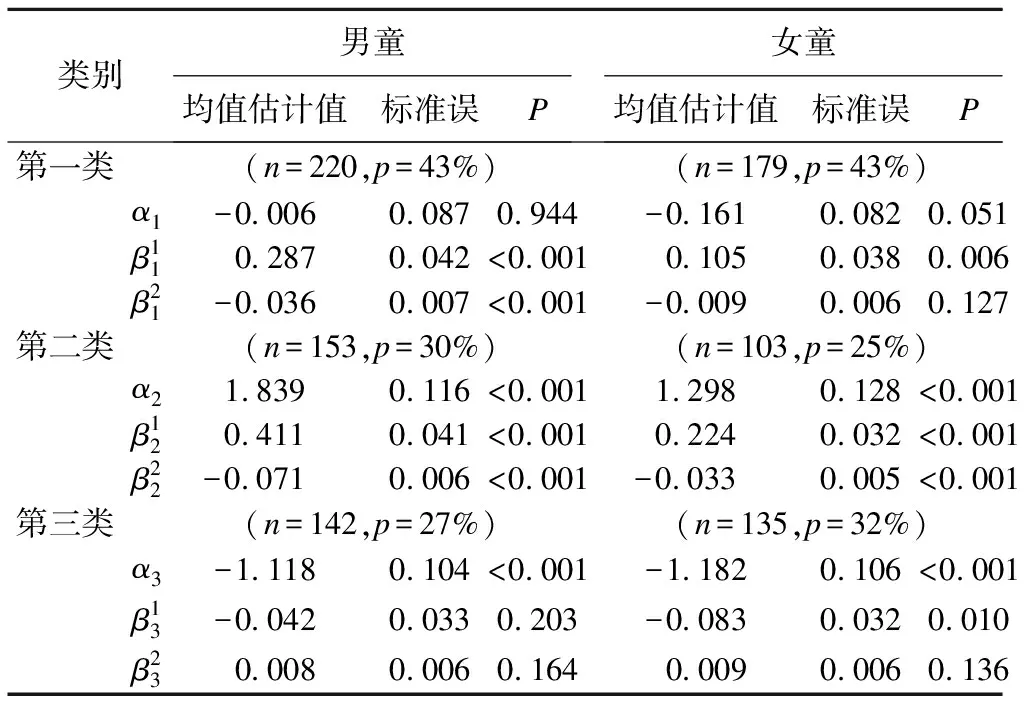
表3 學齡兒童BMI-Z發展趨勢的LCGM模型參數估計結果

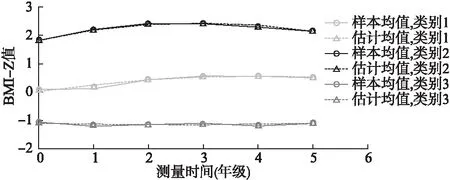
圖1 男童LCGM增長趨勢圖(樣本均值和估計均值)

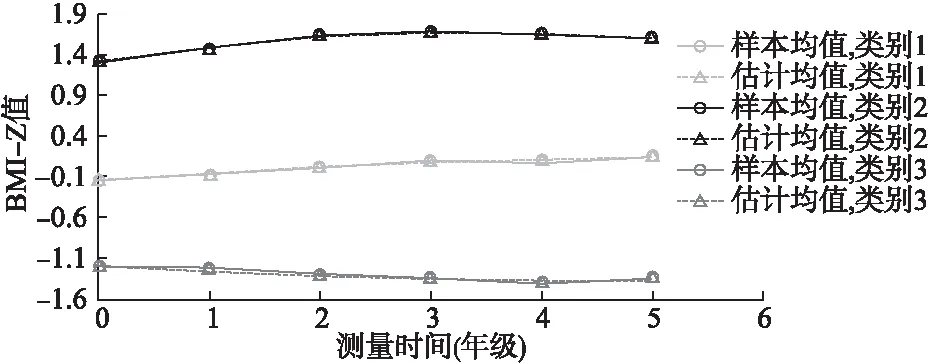
圖2 女童LCGM增長趨勢圖(樣本均值和估計均值)

3.兒童身高變化影響因素的多元回歸分析

多元回歸模型的因變量為6年身高增長值，自變量為基線身高和LCGM確定的亞組分類，其中，將“穩定組”設置為對照組。結果顯示男女童中肥胖組與穩定組對比，身高變化差異均無統計學意義(P>0.05)；而男女童偏瘦組均比穩定組平均身高降低。兩組結果提示，體重增加并不能使得身高增加，而偏瘦會使身高增加不足。結果見表4。

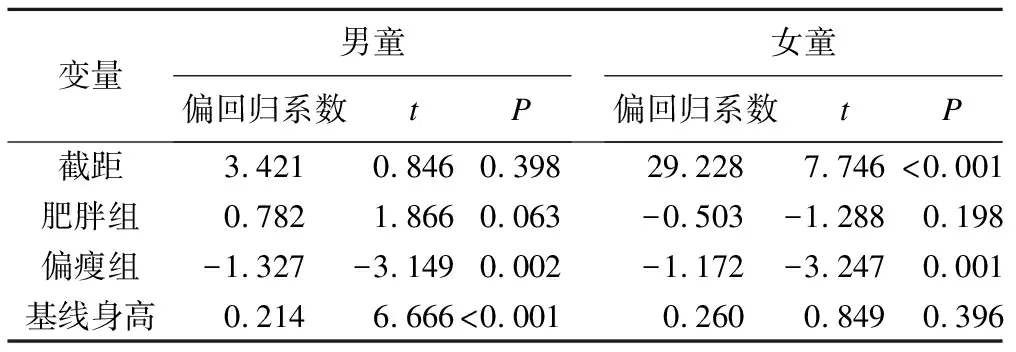
表4 學齡兒童身高增長影響因素的logistic回歸結果

4.兒童BMI-Z的GMM模型擬合結果

運用GMM模型對兒童的BMI-Z值增長情況進行群體異質性分析的過程和LCGM類似。比較不同曲線及不同類別模型的相關擬合評價指標，男童含2個潛在類別二次增長的GMM模型擬合較好，模型參數估計結果見表5，增長趨勢圖見圖3。在第一類別中，男生BMI-Z變化的特點是初始值略低于標準值，隨時間變化較緩慢增長，但增長速度減慢，命名為“穩定增長組”；截距、斜率、二次項系數的方差均有統計學意義，說明這一亞組個體間的BMI-Z初始值、增長率和增長加速度均存在差異；這一類別中增長特征參數間的協方差有統計學差異，表明，男生BMI-Z初始值與斜率、增長加速度有關聯，BMI-Z初始值越高，增長速度越快，增長加速度會減緩。在第二類別中，男生初始值高于標準值，且隨年齡增長而增長，增長速度減緩，命名為“肥胖增長組”；男生這一亞組中截距、斜率、二次項系數的方差分別為2.238(P<0.05)、0.167(P<0.05)、0.001(P=0.101)，說明該類別的男生BMI-Z初始值和增長率存在個體差異，而增長速度沒有個體差異；該組協方差結果表明，男生BMI-Z初始值與增長斜率、增長加速度均有關聯，BMI-Z初始值越高，增長速度越慢，但增長加速度增大。

表5 男童體重發展趨勢的GMM模型參數估計結果

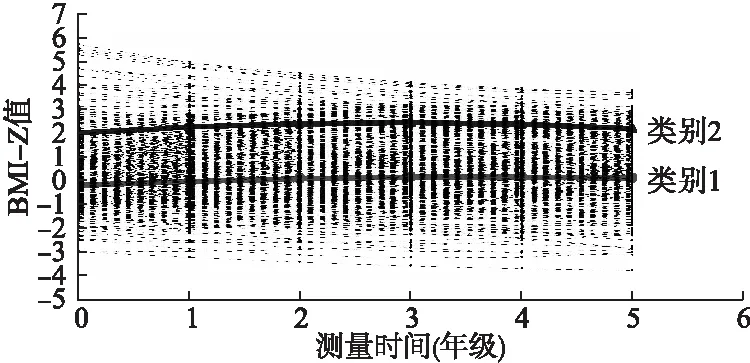
圖3 男童GMM增長趨勢圖(樣本均值和估計均值)

GMM模型在本例女童中應用的效果不佳，根據模型擬合評價指標提示，女童含2個潛在類別二次增長的GMM模型擬合較好。但從表6中可以看出，第一亞組中人數占比為98%，第二亞組人數占比只為2%，研究者普遍認為分類結果中每組人數至少要大于等于5%樣本量[9]。亞組中樣本數量過少，模型分類結果的可靠性低。女童BMI-Z的增長趨勢圖見圖4。

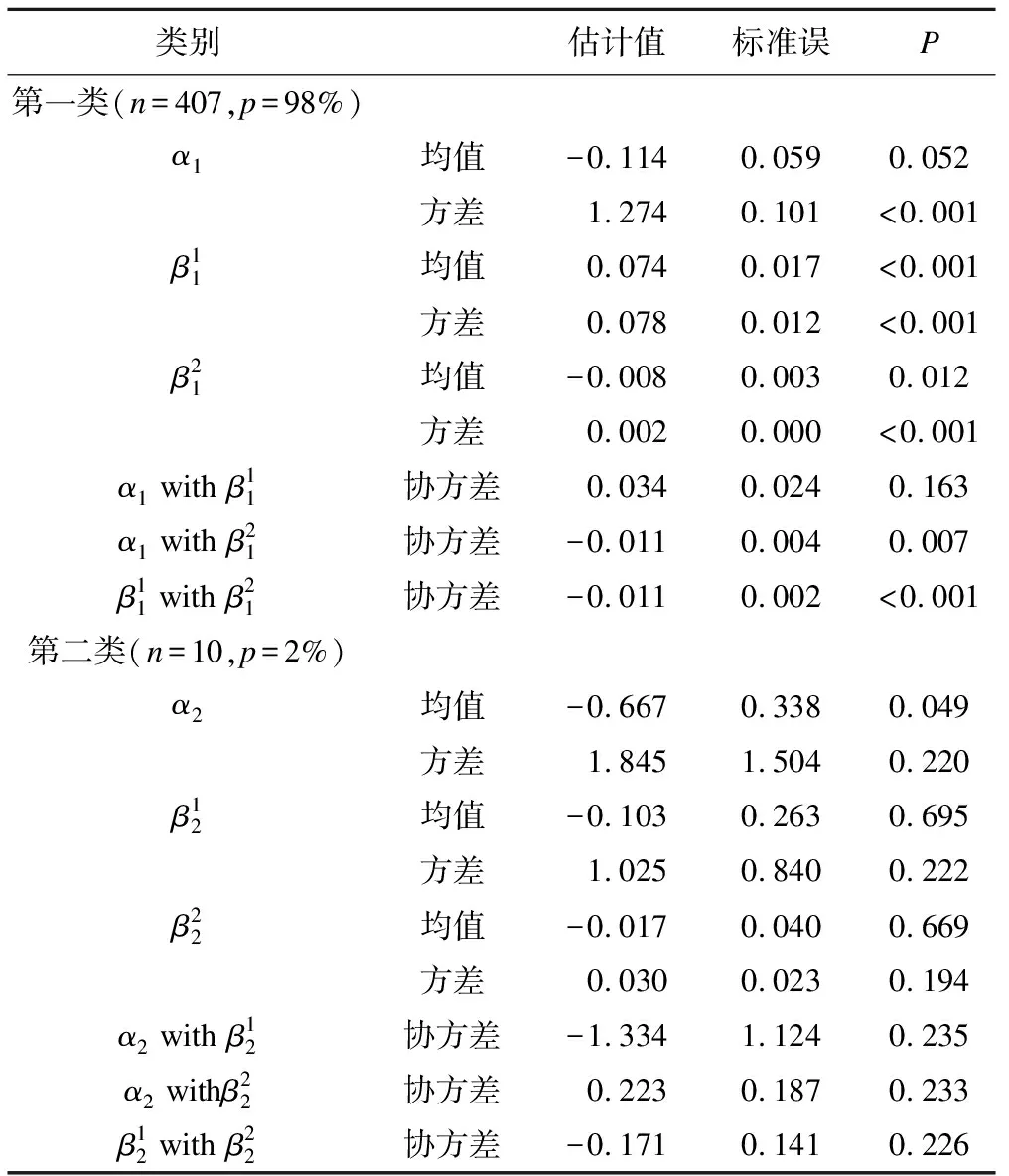
表6 女童體重發展趨勢的GMM模型參數估計結果

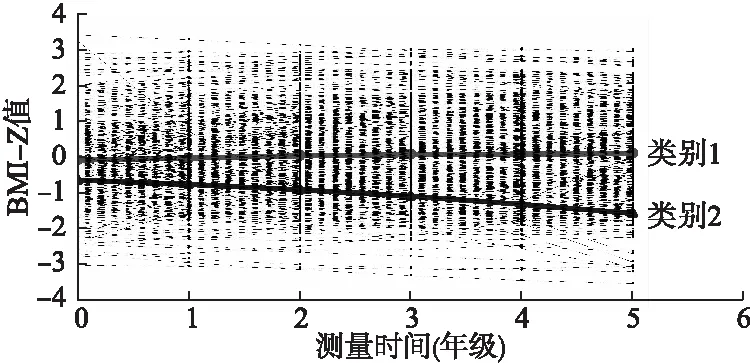
圖4 女童GMM增長趨勢圖(樣本均值和估計均值)

討 論

以往許多關于學齡兒童BMI的研究重點關注的是兒童肥胖率與超重率[10-11]，但探索兒童隨著年齡增長BMI的發展軌跡可以揭示體重的動態變化。學齡兒童在生長發育期間，存在著不同體重變化軌跡的亞群體[12]。本文基于LCGM和GMM兩個模型探索了學齡兒童BMI的變化軌跡，研究發現學齡男女生均存在不同類型的變化軌跡，且回歸模型提示“肥胖組”身高增長并不顯著，說明超重肥胖并不能對身高有所貢獻。故應積極對此類人群體脂進行干預與控制，促進兒童體質健康發展。

關于學齡兒童BMI的隊列研究中，常用的研究方法為傳統的線性混合模型，這樣的方法假定所有人群來自同一體，即群體內每個個體的生長軌跡具有相同的截距和斜率等增長參數，顯然這種方法對異質性較強的兒童群體有很大的局限性。將潛在類別引入增長模型中，既可以刻畫學齡兒童的BMI增長趨勢又可以探討是否存在不同的潛在亞組。GMM模型允許亞組內存在個體差異，而LCGM模型中假設各個亞群的發展軌跡不存在個體差異。兩種模型的最大優點在于，將連續潛變量和分類潛變量結合起來，通過分類潛變量將研究總體分為不同的亞群，根據連續潛變量來描述不同亞群的增長趨勢，甚至可以識別亞群內個體間是否存在差異[3]。因此GMM和LCGM是分析縱向數據的兩種較先進的方法。

由于GMM模型允許潛變量方差與協方差的估計，故對有些數據模擬效果不佳。在本研究中運用GMM模型對女童BMI-Z進行群體異質性分析時，分類結果出現某類別樣本數量過少的情況，模型分類結果的可靠性低。該模型分類精確性的主要影響因素為潛類別間距離和類別內方差，若潛類別間距離越小，模型分類效果越差；若類別內方差越大，類別之間重疊的部分越大，則將個體劃分到特定類別組就越困難[13-14]。因此GMM和LCGM模型的選擇性與適用性也是未來研究中需要不斷總結的問題。