ARIMA乘積季節模型在鄭州市肺結核月發病趨勢預測中的應用*
周 揚 梁士杰
【提 要】 目的 建立鄭州市近年肺結核月發病的ARIMA乘積季節模型(SARIMA)并進行預測,探討該模型在鄭州市肺結核早期預測預警中的可行性。方法 以鄭州市2011-2018年肺結核月發病數為基礎,建立適合鄭州市肺結核ARIMA乘積季節模型,利用R語言的auto.arima( )代碼自動得到最優模型后對2019年肺結核發病數進行預測。結果 構建的鄭州市肺結核月發病預測模型為ARIMA( 2,0,0) (0,1,1)12,模型參數均有統計學意義( P<0.05),模型擬合優度AIC=78.45,BIC=94.04,殘差序列為白噪聲( Ljung-Box test Q=17.285,P=0.3674 ),2019年1-12月實際值與擬合值的動態趨勢高度吻合。結論 本研究建立的ARIMA( 2,0,0) ( 0,1,1)12可用于鄭州市肺結核月發病的早期預測。
結核病是由結核分枝桿菌引起的傳染病,主要導致肺部病變,是我國農村居民因病致貧、因病返貧的主要疾病之一[1]。我國是全球第二大結核病高負擔國家,肺結核是我國重點關注丙類呼吸道傳染病[2]。目前,肺結核作為一種慢性傳染病,在我國每年均有大量病例報告。本研究利用季節性自回歸滑動平均模型法( seasonal auto regressive integrated moving average,SARIMA)對鄭州市2011年1月-2018年12月肺結核發病情況進行擬合,旨在為鄭州市肺結核防控工作提供精準預測的科學依據。
資料與方法
1.數據來源
數據來自中國疾病預防控制信息系統,按發病日期統計的2011年1月-2019年12月報告的鄭州市肺結核發病數。
2011年1月-2018年12月的數據用于建立SARIMA預測模型,2019年1-12月的數據用于模型效果檢驗及預測評價。
2.研究方法
ARIMA乘積季節模型是ARIMA(p,d,q)模型與季節性模型ARIMA(P,D,Q)s的混合效應模型[3]。
SARIMA建模過程包括平穩性檢驗、模型識別、模型診斷、模型預測[4],發病數經自然對數轉換后,利用R中的tseries和forecast包,對鄭州市2011-2019年肺結核的發病數據建立SARIMA模型,利用auto.arima( )代碼結合模型參數估計和殘差診斷選擇最優模型,模型構建采用R3.6.3軟件。
結 果
1.流行特征
經自然對數轉換后,發現鄭州市2011年1月-2018年12月肺結核發病有明顯的季節趨勢,呈現年周期性波動,總體呈緩慢降低趨勢。每年11月份至次年3月份為發病高峰,隨后逐月下降。去掉季節性因素后,鄭州市2013年1-2月發病達到高峰,隨后明顯下降,2013年11月后逐漸增加,到2013年6-7月達到最高峰,隨后逐年下降,但2017年有所增加,2018年迅速下降。從殘差趨勢圖來看呈現明顯的規律性自相關趨勢。
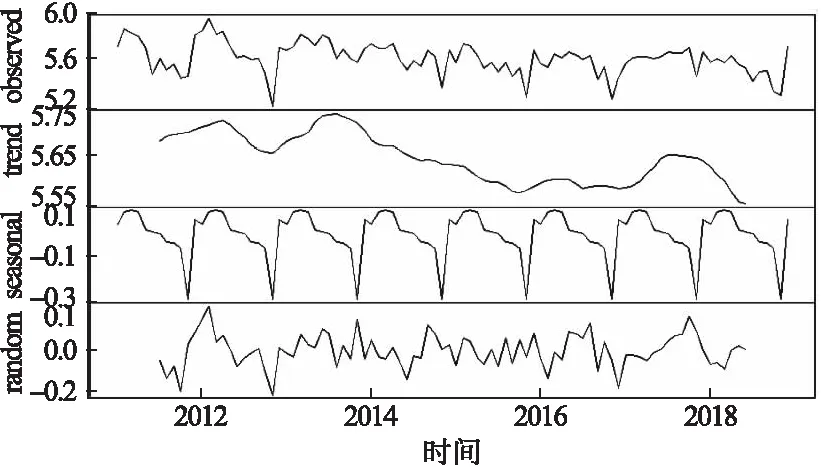
圖1 鄭州市肺結核發病趨勢分解圖
2.SARIMA 模型的構建及評價
利用R軟件中的auto.arima( )代碼自動選取的模型為ARIMA( 2,0,0) ( 0,1,1)12,模型的殘差診斷圖顯示殘差在0附近隨機波動且呈正態分布,對殘差經 Ljung-Box 檢驗后,殘差為白噪聲(Q=17.285,P=0.3674),從殘差自相關圖(ACF)來看,此模型殘差大部分都落入95%可信區間內,說明序列信息已經被充分提取。同時,平均絕對百分誤差MAPE=0.071<10,說明模型的預測精度較高。因此該模型擬合鄭州市2011年1月-2018年12月肺結核發病數據是合適的。

圖2 SARIMA模型殘差分布圖
3.模型預測
圖3為整個樣本期內肺結核的真實值與模型估計值的序列圖,可以看出擬合序列與原序列的變化趨勢基本一致。因此ARIMA(2,0,0)(0,1,1)12模型可用于預測2019年肺結核流行趨勢。
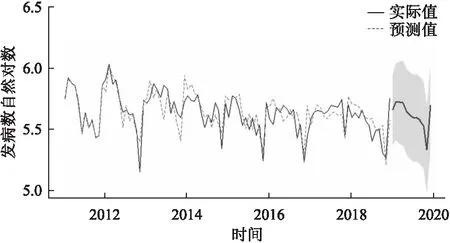
圖3 鄭州市肺結核預測值與實際值擬合圖
利用建立的ARIMA(2,0,0)(0,1,1)12模型對2019年肺結核1-12月發病數進行預測,除2月份外(相對誤差為43.06%),其他月份實際值與預測值相對誤差幅度均低于20%,實際值與預測值誤差率最小0.869%。
2019年鄭州市肺結核用該模型預測合計為3349例,實際發生3399例,差值百分比為1.48%,說明總體預測效果理想。
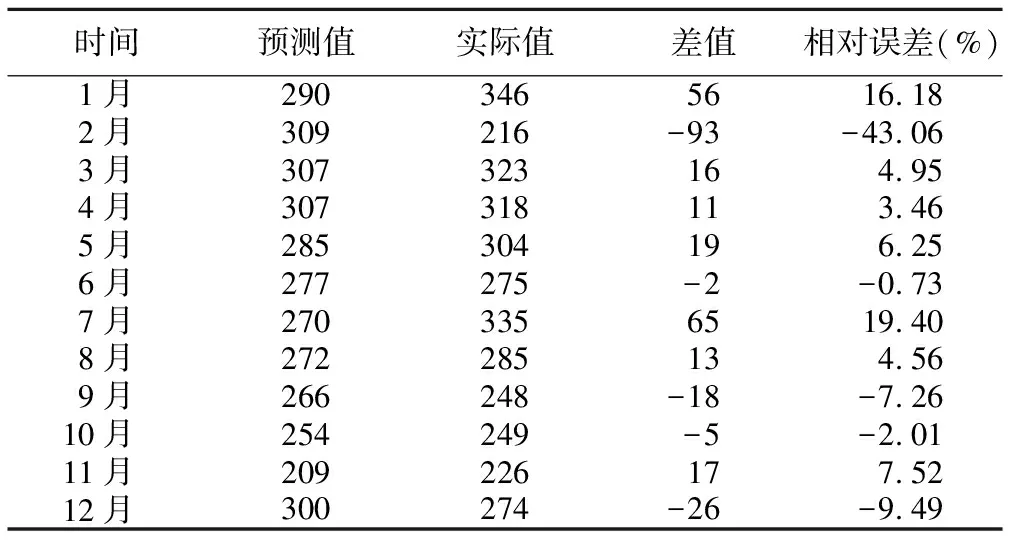
表1 2019年1-12月肺結核發病數與預測數比較
討 論
1.肺結核以ARIMA乘積季節模型進行短期預測是可行的,對于識別慢性傳染病的暴發或流行具有重要意義,有利于提前開展有針對性的傳染病健康宣傳教育和干預措施。目前鄭州市肺結核發病趨勢與全國肺結核總體發病趨勢相同,均呈緩慢下降趨勢,但存在明顯的季節性,本次預測模型預測結果相對精準,可作為預測肺結核的參考模型。
2.利用R語言中的auto.arima( )功能結合模型參數檢驗選擇的最優模型是可行的,可以替代傳統判斷模式,并可提高ARIMA模型中參數確定的效率。
3.本次模型擬合評價中,殘差為白噪聲過程統計檢驗顯著性P=0.3674,但該模型依然存在可能的外界影響因素,如氣象因素、空氣污染物、人口流動等,下一步可考慮探索使用廣義加性模型(GAM),將氣象因素和空氣污染物因素納入模型進行擬合[5]。

