線性回歸中回歸稀釋偏倚校正的模擬研究*
中國醫(yī)學(xué)科學(xué)院 北京協(xié)和醫(yī)學(xué)院 國家心血管病中心 阜外醫(yī)院 醫(yī)學(xué)統(tǒng)計(jì)部(102300)白銀曉 王子悅 柴 昊 趙延延 范肖雪 李 衛(wèi) 王 楊
【提 要】 目的 比較Peto-MacMahon非參數(shù)法(PM)和Rosner回歸校準(zhǔn)法(RC)對(duì)線性回歸中回歸稀釋偏倚的校正效果,同時(shí)討論不同情況下得到回歸系數(shù)最佳校正效果時(shí)所需要的最小樣本量。方法 用Matlab軟件隨機(jī)模擬產(chǎn)生重復(fù)測(cè)量數(shù)據(jù),建立線性回歸模型,用PM法和RC法進(jìn)行校正,比較設(shè)定的真實(shí)系數(shù)與校正前、后回歸系數(shù),評(píng)價(jià)校正效果。結(jié)果 總體樣本量很大時(shí)(大于10000),無論測(cè)量誤差的大小,當(dāng)重復(fù)測(cè)量樣本量達(dá)到總體樣本量的10%~30%,回歸系數(shù)能達(dá)到最佳校正效果;兩種方法穩(wěn)定性差異無統(tǒng)計(jì)學(xué)意義,但PM法在計(jì)算上有更大的優(yōu)勢(shì)。總體樣本量較小時(shí)(小于300),無論測(cè)量誤差的大小,當(dāng)重復(fù)測(cè)量樣本量達(dá)到總體樣本量的15%~30%,回歸系數(shù)能達(dá)到最佳校正效果;但當(dāng)測(cè)量誤差很大,樣本量小于50時(shí),RC法更穩(wěn)定。結(jié)論 無論測(cè)量誤差的大小,當(dāng)重復(fù)測(cè)量數(shù)據(jù)達(dá)到一定樣本量時(shí),兩種方法對(duì)回歸系數(shù)的校正均有很好效果。在測(cè)量誤差很大,且重復(fù)測(cè)量數(shù)據(jù)很少時(shí),建議采用RC法進(jìn)行校正;在其他情況下,建議采用PM法。
統(tǒng)計(jì)分析過程中,在收集數(shù)據(jù)時(shí),經(jīng)常由于測(cè)量工具的不精確或個(gè)體差異等原因,導(dǎo)致測(cè)量誤差的產(chǎn)生。MacMahon發(fā)現(xiàn)[1],當(dāng)利用自變量的單一測(cè)量值進(jìn)行回歸分析時(shí),由于隨機(jī)測(cè)量誤差的存在會(huì)導(dǎo)致回歸系數(shù)的估計(jì)值比真值偏小,這種現(xiàn)象被稱為回歸稀釋偏倚[2-3]。如何消除上述偏倚,獲得真實(shí)的關(guān)聯(lián)程度估計(jì)是流行病和臨床研究中的一個(gè)普遍問題。
在大型的流行病學(xué)或前瞻性臨床研究中,研究者會(huì)在不同的隨訪時(shí)點(diǎn)對(duì)被觀察對(duì)象某些生理指標(biāo)(例如心率、血壓等)進(jìn)行重復(fù)測(cè)量,利用這些重復(fù)測(cè)量數(shù)據(jù)(同分布),可以計(jì)算回歸系數(shù)偏倚的程度、并獲得校正因子(回歸稀釋系數(shù))值,通過該校正因子、可對(duì)基于由單一基線觀測(cè)值得到的回歸系數(shù)估計(jì)值進(jìn)行調(diào)整,從而獲得更接近“真實(shí)”關(guān)聯(lián)程度的估計(jì)結(jié)果。
本文將對(duì)文獻(xiàn)報(bào)道中常用的Peto-MacMahon非參數(shù)法和Rosner回歸法進(jìn)行對(duì)比分析,通過隨機(jī)模擬比較,探討兩種方法在不同樣本量、不同測(cè)量誤差的前提下對(duì)回歸稀釋偏倚的校正效果。
模型建立與方法
1.重復(fù)測(cè)量數(shù)據(jù)與“回歸稀釋偏倚”校正
考慮在進(jìn)行關(guān)聯(lián)分析時(shí)普遍使用的線性模型:
Y=α+β·X+ε
(1)
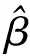
當(dāng)協(xié)變量X為重復(fù)測(cè)量數(shù)據(jù)時(shí),設(shè)首次測(cè)量值為W,重復(fù)測(cè)量值為T。有
(2)
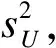
將首次測(cè)量值W作為真實(shí)值X代入(1)式,有
Y=α*+β*·W+δ
(3)
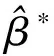

(4)

2.Peto-MacMahon 非參數(shù)估計(jì)法

(5)
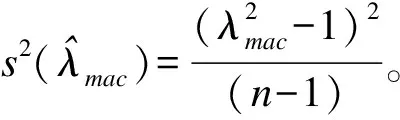
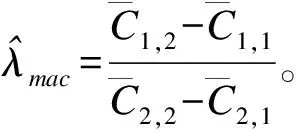
3.Rosner回歸估計(jì)法
對(duì)于由(2)式定義的重復(fù)測(cè)量數(shù)據(jù),可在首次測(cè)量值W和重復(fù)測(cè)量值T間建立線性回歸模型[9]
T=αT|W+βT|W·W+τ
(6)
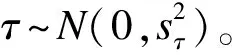
(7)
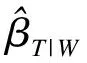
模擬分析
1.模擬設(shè)計(jì)
假設(shè)預(yù)進(jìn)行一真實(shí)的臨床關(guān)聯(lián)性研究,評(píng)價(jià)血壓水平與某特定定量結(jié)局指標(biāo)間的關(guān)聯(lián)。首先假定存在N=10000的真實(shí)總體,設(shè)定預(yù)后因素收縮壓X~N(110,102),測(cè)量誤差U1,U2~N(0,22)。設(shè)定回歸系數(shù)的真實(shí)值β=-4,-2,-1,-0.5,0.5,1,2,4,分別建立線性回歸模型Y=β·X,產(chǎn)生因變量Y的真值。由(2)式可產(chǎn)生首次測(cè)量值W和重復(fù)測(cè)量值T。

其余假設(shè)不變,設(shè)測(cè)量誤差U1,U2~N(0,102),重復(fù)上述模擬步驟,討論測(cè)量誤差的變化對(duì)回歸系數(shù)產(chǎn)生的影響。
再考慮樣本量較小的情況。設(shè)總體樣本量N=300,重復(fù)測(cè)量樣本量不少于總體樣本量的10%[10],取n=30,50,80,100,150,200,測(cè)量誤差分別為U1,U2~N(0,22)和U1,U2~N(0,102),重復(fù)上述模擬步驟。
考慮U1,U2不同分布的情況。其余假設(shè)不變,測(cè)量誤差U1~N(0,22),U2~N(0,102),重復(fù)上述模擬步驟。盡管MacMahon法不適用于測(cè)量誤差不同分布的情況,但將兩種方法得到的結(jié)果進(jìn)行秩和檢驗(yàn),若檢驗(yàn)結(jié)果為兩種方法得到的校正因子無顯著性差異,由于MacMahon法在計(jì)算上的優(yōu)勢(shì),在實(shí)際中仍可考慮用MacMahon法。
2.模型效果評(píng)價(jià)標(biāo)準(zhǔn)
評(píng)價(jià)模型校正效果的標(biāo)準(zhǔn)有兩個(gè):(1)校正后回歸系數(shù)與設(shè)定真實(shí)值之差的絕對(duì)值。絕對(duì)值越小說明校正效果越好。(2)校正后系數(shù)的標(biāo)準(zhǔn)差。標(biāo)準(zhǔn)差越小說明校正效果越穩(wěn)定。本研究設(shè)定校正后的回歸系數(shù)在[β-0.01β,β+0.01β]區(qū)間時(shí),校正效果好[11]。可根據(jù)此標(biāo)準(zhǔn)確定兩種方法分別達(dá)到回歸系數(shù)最佳校正效果所需要的最小樣本量。
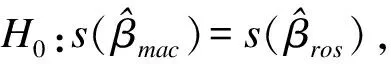
3.模擬結(jié)果

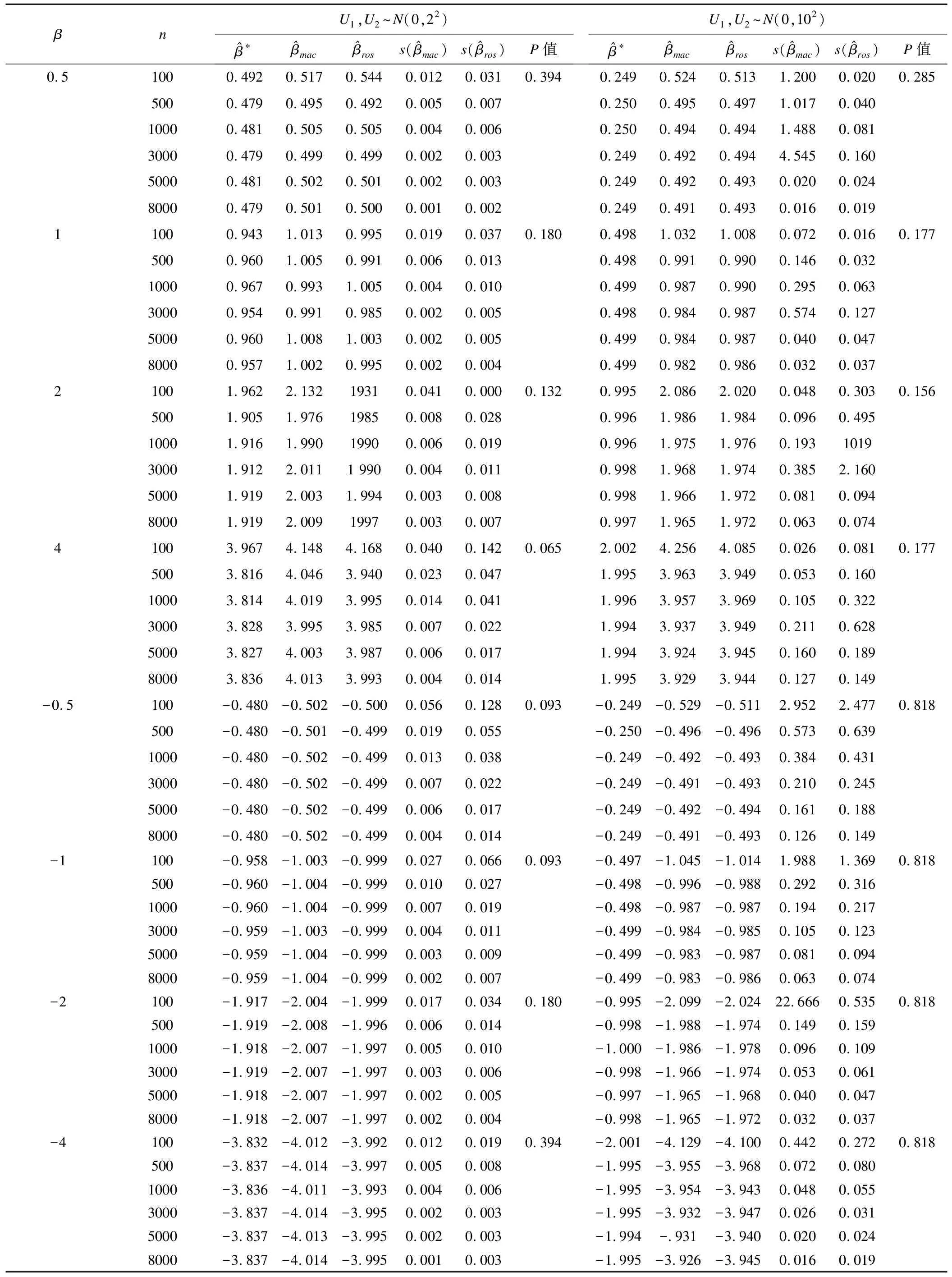
表1 MacMahon法和Rosner法對(duì)回歸系數(shù)調(diào)整的效果(N=10000)
穩(wěn)定性分析:在任何β取值下,P>0.05,兩種方法的穩(wěn)定性差異無統(tǒng)計(jì)學(xué)意義,可認(rèn)為估計(jì)效果相同。由于MacMahon方法在計(jì)算時(shí)的巨大優(yōu)勢(shì),故采用MacMahon非參數(shù)的方法。

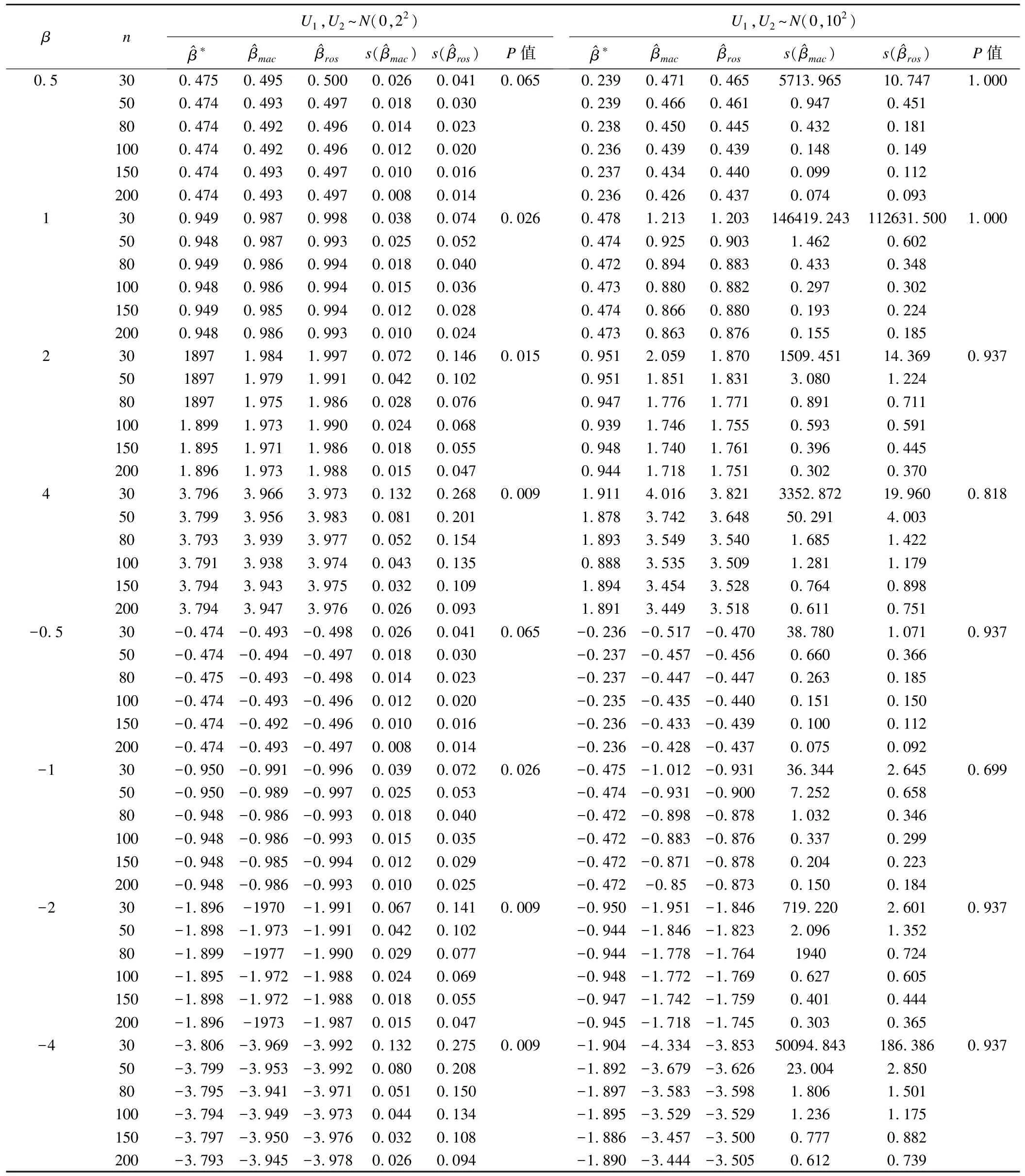
表2 MacMahon法和Rosner法對(duì)回歸系數(shù)調(diào)整的效果(N=300)
因此,當(dāng)總體樣本量較小時(shí),重復(fù)測(cè)量數(shù)據(jù)樣本量達(dá)到總體樣本量的15%~30%時(shí),調(diào)整后的系數(shù)估計(jì)值就能達(dá)到較好的效果。
穩(wěn)定性分析:(1)當(dāng)方差s2=22,β=1,2,4,-1,-2,-4條件下,P<0.05,說明兩種方法的穩(wěn)定性差異有統(tǒng)計(jì)學(xué)意義。由于利用Rosner方法估計(jì)出的系數(shù)標(biāo)準(zhǔn)差較大,即調(diào)整效果不穩(wěn)定,因此選擇MacMahon法更合適。(2)當(dāng)方差s2=102,在任何β條件下,P>0.05,兩種方法的穩(wěn)定性差異無統(tǒng)計(jì)學(xué)意義,可認(rèn)為估計(jì)效果相同。由于MacMahon方法在計(jì)算時(shí)的巨大優(yōu)勢(shì),采用MacMahon非參數(shù)的方法。但n=30時(shí),MacMahon方法所得到的系數(shù)標(biāo)準(zhǔn)差非常大,說明方法非常不穩(wěn)定,且此時(shí)利用Rosner方法在計(jì)算上并不會(huì)比MacMahon方法花費(fèi)時(shí)間更多,因此當(dāng)重復(fù)測(cè)量數(shù)據(jù)小于50時(shí),應(yīng)選擇Rosner方法。
(3)兩次測(cè)量誤差方差不同時(shí)(表3),可看出,此時(shí)計(jì)算的校正因子比測(cè)量誤差的方差相同時(shí)得到的校正因子值增大,與實(shí)證結(jié)果相符。且盡管MacMahon理論上不適用于方差不同的情況,但從模擬的結(jié)果可知,在任何β條件下,P>0.05,即由兩種方法得到的校正因子間差異無統(tǒng)計(jì)學(xué)意義。因此在實(shí)際中,若樣本量較大時(shí),考慮MacMahon法計(jì)算上的優(yōu)勢(shì),仍然建議選擇MacMahon法對(duì)回歸系數(shù)進(jìn)行校正。

表3 兩次測(cè)量誤差不同校正因子與統(tǒng)計(jì)學(xué)P值(U1~N(0,22),U2~N(0,102))
討 論
上述的模擬分析表明,未校正的回歸系數(shù)估計(jì)值均小于真實(shí)回歸系數(shù)值,與“回歸稀釋偏倚”現(xiàn)象理論結(jié)果相符。在測(cè)量誤差固定的情況下,只要達(dá)到一定樣本量,對(duì)回歸系數(shù)值估計(jì)的校正均有很好的效果。尤其當(dāng)測(cè)量誤差較大時(shí),未經(jīng)校正的系數(shù)估計(jì)值非常不準(zhǔn)確,對(duì)其進(jìn)行校正顯得尤為重要。根據(jù)模擬研究結(jié)果可知,當(dāng)測(cè)量誤差較大(測(cè)量誤差的方差大于樣本分布的方差),樣本量小于50時(shí),由于Rosner回歸法穩(wěn)定性更好,應(yīng)采用Rosner回歸法;其余情況,從計(jì)算效率和穩(wěn)定效果上考慮,均可采用Peto-Macmahon法。
在實(shí)際研究中,當(dāng)遇到重復(fù)測(cè)量數(shù)據(jù)問題進(jìn)行回歸系數(shù)估計(jì)或者進(jìn)一步估計(jì)危險(xiǎn)率等指標(biāo)時(shí),需要根據(jù)觀測(cè)數(shù)據(jù)的分布等性質(zhì)選擇適當(dāng)?shù)姆椒▽?duì)回歸系數(shù)進(jìn)行校正。盡管此時(shí)我們不知道真實(shí)系數(shù)值的大小,只要樣本量達(dá)到一定量的條件,就能有很好的校正的效果。需要注意的是,實(shí)際問題中,進(jìn)行回歸稀釋偏倚校正時(shí),應(yīng)首先考慮所關(guān)注的預(yù)后變量其重復(fù)測(cè)量數(shù)據(jù)間是否具有獨(dú)立性,在回歸稀釋問題的場(chǎng)景下,重復(fù)測(cè)量數(shù)據(jù)間理論上不獨(dú)立、但應(yīng)滿足條件獨(dú)立(對(duì)應(yīng)測(cè)量誤差),條件獨(dú)立性可考慮通過回歸調(diào)整后,檢驗(yàn)殘差是否獨(dú)立等方法來進(jìn)行判斷。此外,所關(guān)注的重復(fù)測(cè)量來源變量,應(yīng)符合正態(tài)分布,或者將數(shù)據(jù)進(jìn)行適當(dāng)變換(如對(duì)數(shù)變換)后符合正態(tài)分布,在此基礎(chǔ)上再選擇合適的方法對(duì)稀釋系數(shù)進(jìn)行校正。在上述條件無法滿足時(shí),例如重復(fù)測(cè)量數(shù)據(jù)間存在時(shí)間趨勢(shì),那么在分析重復(fù)測(cè)量數(shù)據(jù)與結(jié)局指標(biāo)的關(guān)聯(lián)時(shí),應(yīng)采用具有針對(duì)性且適宜的方法對(duì)回歸稀釋偏倚進(jìn)行矯正[16]。
在亞太群組協(xié)作研究組織(the Asia Pacific Cohort Studies Collaboration,APCSC)研究已發(fā)表的文章中,已有很多作者使用了重復(fù)測(cè)量數(shù)據(jù)來校正回歸稀釋偏倚。如Anushka Patel等人[13]利用重復(fù)測(cè)量的膽固醇含量數(shù)據(jù),Koshi Nakamura等人[14]利用重復(fù)測(cè)量的收縮壓數(shù)據(jù),Mark Woodward等人[15]利用重復(fù)測(cè)量的高密度脂蛋白膽固醇數(shù)據(jù)對(duì)回歸稀釋系數(shù)進(jìn)行校正,進(jìn)而評(píng)估這些因素與結(jié)局死亡率間的關(guān)系。
本文只探討了一個(gè)危險(xiǎn)因素的情況,當(dāng)有多個(gè)危險(xiǎn)因素時(shí),仍可以選擇Rosner方法對(duì)相應(yīng)的稀釋系數(shù)進(jìn)行校正,然而MacMahon法無法對(duì)多因素的回歸模型進(jìn)行處理。此外,MacMahon法和Rosner法均是考慮在基線數(shù)據(jù)的條件下,重復(fù)測(cè)量數(shù)據(jù)是真實(shí)數(shù)據(jù)的無偏估計(jì)。因此校正因子的取值依賴于首次測(cè)量(基線)和重復(fù)測(cè)量的順序。若無法判別一批重復(fù)測(cè)量數(shù)據(jù)中哪些為基線測(cè)量、哪些為重復(fù)測(cè)量,MacMahon法和Rosner法的校正效果均失效,需要從基線數(shù)據(jù)和重復(fù)測(cè)量數(shù)據(jù)間的方差與相關(guān)性角度選擇另外方法如積差相關(guān)系數(shù)法、組內(nèi)相關(guān)系數(shù)法、極大似然法和Rosner方差組件法對(duì)回歸稀釋系數(shù)進(jìn)行校正[8]。同樣,本文的模擬研究并未覆蓋存在多次重復(fù)測(cè)量的場(chǎng)景,因此在就本文結(jié)果做應(yīng)用或外推時(shí),需考慮上述局限性可能造成的影響。

