超音速尾流作用下通氣空泡穩定性及閉合位置數值研究1)

趙小宇 向 敏 張為華 劉 波 李尚中

(國防科技大學空天科學學院,長沙 410073)

引言

隨著海洋戰略地位日益凸顯,圍繞海洋來展開深海環境探索,資源開發以及武器裝備研發變得日趨重要,未來海洋將會是世界各國科技實力角逐的重要戰場.相比于空氣,水的高黏度流體特性帶來的巨大阻力嚴重制約水下航行體的航速和機動性能,通氣空泡減阻技術能實現高效的水下減阻,在水下發射、超高速跨介質導彈等領域極具應用前景.

近年來水下動力技術逐漸成為一個新的研究熱點問題,相較于空氣,一方面水中壓力會阻礙氣體膨脹,噴管出口處形成很高的背壓;另一方面,在水氣巨大的速度差形成的強剪切影響下,導致壓力振蕩,噴管出口環境很不穩定[1-2].針對水下背壓高的問題,可以通過提高發動機燃燒室的壓比,設計噴管出口為過膨脹狀態來解決[3].而噴管出口壓力振蕩的問題還未有行之有效的辦法,降低出口壓力脈動至可控范圍內于工程實踐具有重要意義.

水下射流流體特性研究進展,主要包括Shi 等[4-5]在靜水塔中開展了超音速氣體射流實驗,結果顯示壓力脈動的頻率和噴管內激波振蕩相關聯.Han 等[6]利用一個實驗室尺度的固體火箭發動機在水下開展了推力測試實驗,得出噴管出口處氣泡增長和脫落是導致壓力脈動的主要原因.唐云龍等[7]在VOF 模型基礎上通過添加相變源項,建立了考慮相變的可壓多相流數值方法,并模擬了水下固體火箭發動機產生的高溫燃氣射流.Fronzeo 和Kinzel[8]通過數值仿真研究了不同密度液流環境下氣體射流的演化過程.許昊等[9]通過水洞實驗研究了水流速度對尾噴氣體射流的影響,對比分析有無水流速度兩種情況下,剪切作用差異帶來的氣體射流形態演化過程與壓力脈動特性的變化.Xiang 等[10]考慮了深水環境條件下,過膨脹氣體射流的流動結構和演化過程.

尾噴管出口處的環境,對發動機參數設計來說如此重要,是否可以從流動控制的角度去改善出口壓力振蕩的問題.張孝石等[11]在實驗中觀察到氣體射流直接噴在水中和有空泡包裹前提下噴到水中,兩者形態存在很大差異.Zhang 等[12]研究了水下氣體射流誘導產生的尾空泡問題,并分析了不同類型誘導尾空泡轉變條件.王曉輝等[13]研究了火箭發動機在尾空泡內點火過程,尾空泡的存在有效降低了燃氣射流建立初期形成的極高沖擊壓力,但是尾空泡內仍然存在劇烈的壓力振蕩,從而引起發動機的推力不穩定.

超空泡航行體表面存在4 種基本空泡流型,如圖1 所示.局部空泡流型、尾部閉合空泡流型、雙空泡流型、自由閉合空泡流型.不同的空泡流型導致空泡射流耦合流場結構發生變化,如圖2 所示.特別是第3 種,通氣空泡包裹整個尾流場的情況,空泡是否可以為火箭發動機提供穩定的工作環境,是否可以形成氣幕來降低發動機所產生的噪音,這是非常值得研究的問題.要達到上述目的,前提就是要維持空泡形態的穩定性.

水下射流流體特性和空泡演化過程緊密耦合,相關研究表明高溫、高速氣流直接作用于空泡內流場和空泡界面,可引起空泡界面波動甚至斷裂.Paryshev[14]結合空泡截面獨立擴張原理和空泡尾部閉合模型,提出了兩個無量綱數來判定通氣空泡泄氣模式和穩定性的理論模型,兩個無量綱數與射流總壓和動量相關.Karlikov 等[15]對采用不同噴射方式的通氣空泡開展了實驗研究.研究表明:采用軸向高速噴射氣流時,高速區域壓力降低,導致空泡頸縮斷裂.Karlikov 等[15]指出,噴射速率變化導致空泡表現出不同形態,其本質在于氣流噴射效應引起邊界層氣體流場結構和尾部泄氣方式的改變,進而改變空泡穩定性.Krane 等[16-19]從理論、實驗和計算流體力學3 個角度探討了通氣空泡與尾噴射流之間的相互作用規律,得出: 尾噴射流氣體對空泡剪切層內氣體流動具有較大影響.當射流強度較小時,射流為空泡補氣.當射流強度足夠大時,在射流動量影響下,空泡泄氣模式最終轉變為震蕩泄氣模式,空泡失穩.周后村[20]開展了一系列實驗研究,觀測到了尾噴流作用下新型的震蕩/雙渦管耦合泄氣機制.發現射流強度足夠大時將導致連續空泡界面發生頸縮,而射流誘導的渦結構與空泡界面的相互作用是引起空泡失穩的主要原因.

總的來說,Paryshev 理論較好的建立了亞音速射流和空泡耦合作用模型,但實際工程實踐中,噴流多為超音速工況,需要考慮氣體的可壓縮性和總壓損失.除此之外,射流和空泡相對位置關系的變化等都會影響到不同模式轉化臨界條件.Paryshev 理論模型尚不足以解決上述問題,且未能對射流作用下空泡形態進行理論描述.本文利用VOF 耦合水平集(level set)界面追蹤方法,考慮氣體的可壓縮性,針對自由閉合流型的通氣空泡,改變射流強度和模型長度,展開了一系列的空泡和超音速尾射流相互作用的數值模擬,重點分析了通氣空泡的穩定性和閉合位置.

1 可壓多相流數值方法

通氣空泡和超音速尾噴流相互作用的過程中,一方面要考慮射流作用下空泡界面的非定常演化特性,另一方面要考慮氣體可壓縮性的影響.空泡內氣體可壓縮性越明顯,通氣空泡越不穩定[21-22].本文基于商業軟件Fluent 平臺,只考慮氣相可壓,并通過CLSVOF 方法來模擬空泡界面的演化過程.

1.1 控制方程

多相流中VOF 模型的連續方程,動量方程,能量方程表達如下

式中p,T,u,ρ ,μ 和α 分別代表壓力、溫度、速度、密度、黏性系數和相體積分數.keff代表導熱系數. ρmg為體積力,FCSF為表面張力.角標m,w,g分別表示混合相、液相和氣相.混合相的物性參數定義為

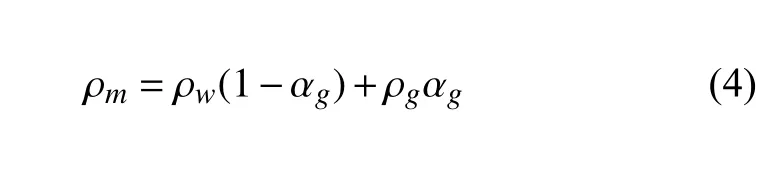
混合相聲速的計算公式如下

1.2 VOF 耦合level set 界面捕捉方法

在Bourlioux[23],Sussman 和Puckett[24]提出的耦合VOF 和level-set (CLSVOF)方法中,通過耦合求解體積分數方程和level-set 函數方程來捕獲和跟蹤界面.主要思想為: 首先利用VOF 方法求解單位網格內的相體積分數,得到界面位置,這樣可以確保質量守恒.再利用體積分數初始化level-set 距離函數,通過求解距離函數得到界面分布情況,采用levelset 方法可以得到準確的界面曲率和法向量.VOF 方法中體積分數輸運方程如下

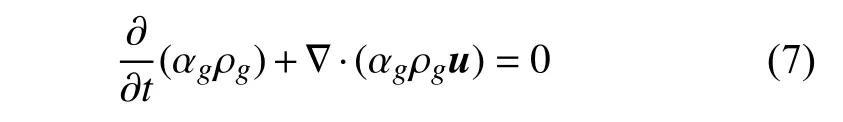
level-set 方法中符號距離函數 φ(x,t) 表達式如下

式中d代表距界面的距離.對于給定的速度場u,求解level-set 函數對流方程確定界面的演化

由于數值計算過程中格式誤的差影響,經式(9)求解得到的距離函數包含誤差,不是真實的界面位置.因此,通常需要對距離函數進行重新初始化,方程如下

其中,角標 τ 為虛擬時間.s ignφ0為符號函數,其定義為

H(φ0)為Heaviside 函數,與體積分數相關聯,其定義為

其中,參數 ε=1.5Δx,Δx為網格尺度.

Level-set 模型中界面單位法向量、曲率計算公式如下

計算過程中,每個迭代時間步都需要重新初始化 φ(x,t) 函數使其保持符號距離函數的特征.CLSVOF 算法中通過幾何方法進行符號距離函數重新初始化.即由相體積分數確定界面單元中各相分別占單元的幾何比例,即單元格內的切割比例,而level-set 函數的梯度確定界面的方向,即單元格內的切割方向.界面重構后,由幾何方法計算符號距離函數.

1.3 湍流模型

k-ωSST 湍流模型由k-ε模型和k-ω模型加權平均得到[25],兼顧兩者的優勢,在邊界層分離流動和空化流動中具有廣泛的應用.其湍動能k和湍流比耗散率ω的輸運方程可以表達如下

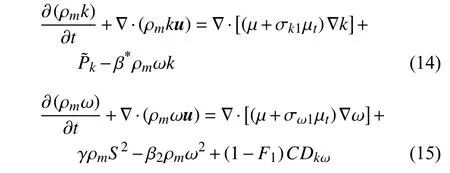
式中,β*,β2,σk1,σω1,γ 為模型常數,為湍動能生成項

湍流黏度 μt定義為

式中,S為應變率,a1為模型常數.混合函數F1和F2分別為

各模型參數取值如表1 所示.

表1 k-ω SST 湍流模型參數Table 1 k-ω SST model parameters

1.4 幾何模型、網格劃分及邊界條件

實驗模型采用回轉體結構,主要由頭部空化器、中間段(共4 個長度)和尾噴管構成,其外形示意圖及尺寸如圖3 所示.尾噴管結構設計為喉部和出口的擴張比為2.25,出口設計馬赫數Mae=2.2.在不同射流流量條件下,射流的出口速度范圍可以覆蓋亞音速到超音速.

圖3 幾何模型(單位: mm)Fig.3 The geometric model (unit: mm)

計算域和邊界條件設置,以及噴管出口附近網格如圖4 和圖5 所示.入口速度5 m/s,出口壓力80 kPa,遠場為無滑移壁面邊界條件.通氣和射流入口采用質量流量邊界條件,通氣質量流量為0.000 1 kg/s.并在空化器附近和噴管出口附近設置壓力監測點A和B.網格采用結構網格,網格量為180 萬,在空泡界面處和噴管出口處做了網格加密處理.

圖4 計算域和邊界條件Fig.4 Computation domain and boundary condition

圖5 模型附近結構網格Fig.5 Employed structured mesh near the model

2 數值仿真結果

2.1 不同射流強度計算結果分析

2.1.1 噴管出口激波結構

仿真計算過程中對比了4 個入口質量流量.圖6展示了t=5 ms 時,不同入口質量流量條件下噴管出口速度云圖及激波結構,其中代表質量流量,代表射流出口處無量綱動量.由于此時空泡界面還未變化,射流直接噴在氣的環境中,未受到水介質的影響.當=0.001 48 kg/s 時,為管內正激波,出口流動為亞音速流動.當=0.002 22 kg/s 時,管內的正激波靠近噴管出口,出口流動仍為亞音速流動.當=0.002 96 kg/s時,管口為相交斜激波,出口速度達到設計馬赫數2.2,為過膨脹狀態.

圖6 不同入口質量流量條件下噴管出口速度云圖及激波結構Fig.6 Velocity cloud plot and shock wave structure at the nozzle exit as the inlet mass flow varies

圖6 不同入口質量流量條件下噴管出口速度云圖及激波結構(續)Fig.6 Velocity cloud plot and shock wave structure at the nozzle exit as the inlet mass flow varies (continued)

2.1.2 射流作用下空泡界面的演化過程

超音速尾流作用下,射流卷吸周圍空泡內氣體,導致空泡內部出現質量流動的不平衡,空泡界面會經歷一個復雜演化過程,來達到新的平衡狀態.圖7展示了空泡界面的非定場演化過程.射流開啟后,首先大量的氣體使得空泡發生膨脹,膨脹部分向后運動,接著空泡由于形態拉長而出現中間部分頸縮,進一步出現斷裂,空泡整體回縮,長度變短.之后,空泡開始進入周期性震蕩泄氣階段.射流強度越強,空泡出現頸縮斷裂的時間越早,更快的進入到震蕩泄氣階段.當射流的強度超過一定臨界值以后,在空泡尾部會出現液體射流沖擊空泡界面的情況,從而進一步導致空泡失穩.

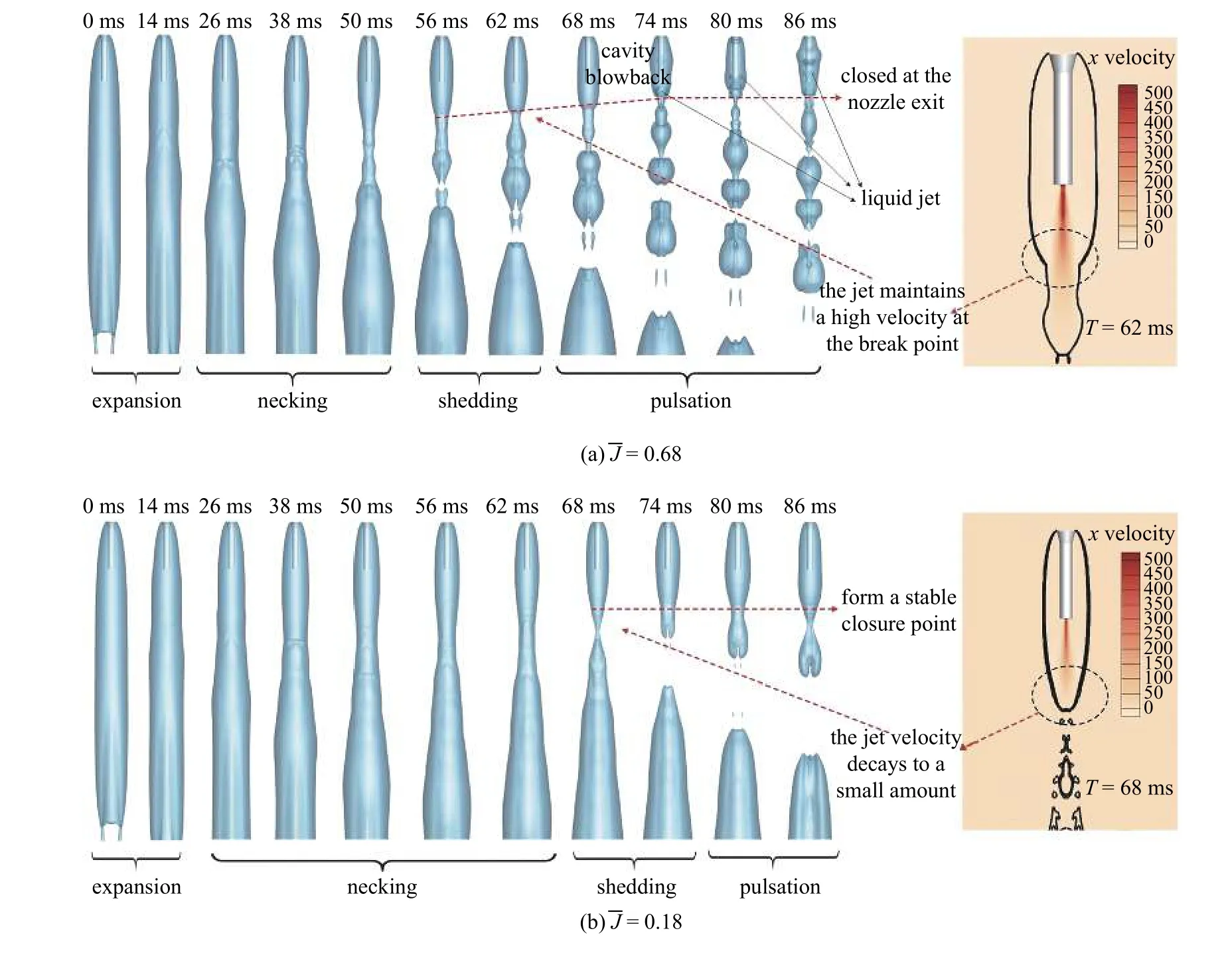
圖7 空泡界面演化過程Fig.7 Cavity inteface evolution process

2.1.3 液體回射流的形成機制及空泡失穩過程

通氣空泡尾部一般存在回射流泄氣和雙渦管泄氣兩種典型模式[26].其中,雙渦管模式時空泡尾部形成穩定反向螺旋的雙渦管流動.而回射流泄氣以空泡尾部非穩定回注射流的出現和螺旋式渦團的脫落為特征,值得注意的是,液體回射流只出現在空泡的下表面.2012 年Savchenko 和Savchenko[27]指出Rayleigh-Taylor (RT)不穩定性機制是導致界面不穩定的主要原因.氣體填充界面凹陷過程中導致液流飛濺,從而出現回射現象.2019 年Wu 等[28]利用流動可視化技術做了更多詳細的解釋,由于浮力的影響空泡尾部會上飄形成一定的角度 α,如圖8 所示,回射現象的發生和這個角度有著緊密的聯系.氣液界面外部水流一側在空泡尾部為擴張流動,邊界層內由于重力分量Gsinα 形成很強的逆壓力梯度,從而導致液流穿透界面,空泡內壓差會進一步增強液體射流動能,最終只在空泡尾部下底面出現回射現象.

圖8 通氣空泡內液體回射流形成機制Fig.8 Formation mechanism of liquid back-jet flow in the ventilated cavity

對于尾噴流作用下的通氣空泡在夾斷過程會出現兩種情況,如圖9 所示,第一種射流的強度較弱,空泡夾斷以后空泡尾部為尖尾型,與圖7 中=0.18工況一致,此時空泡尾部夾角角度很小,難以形成回射.第二種情況射流的強度較強,射流在空泡斷裂點保持著很高的速度,氣體很快形成二次膨脹使得空泡尾部變成凹型尾,與圖7 中=0.68 工況一致.在凹陷處的上表面,重力作用使得凹陷的角度更大,在下表面重力作用趨向于使得界面變平,結果使得液體射流更容易形成于空泡尾部的上表面,出現上下不對稱的結果.另外射流的速度越高,空泡內側的壓力越低,空泡內外壓差導致空泡尾部界面的回擊,同時為液體射流提供足夠的能量,與純通氣空泡相比,此時向前沖擊液體射流擁有更強的動能.

圖9 尾噴流作用下液體回射流形成機制Fig.9 Formation mechanism of liquid back-jet flow under the action of a tail jet

空泡穩定性受到很多流動參數的影響,為了確定哪些流動參數才是關鍵所在,因而對空泡的破壞過程展開了詳細研究.圖10 展示了液體回射流作用下通氣空泡的失穩過程,液體回射形成之后,沿著空泡內氣體回流的方向向前運動,直至接觸空化器附近的界面,并與迎面的來流發生碰撞,對空泡產生巨大破壞,空泡界面已經嚴重扭曲變形,接著空泡界面的振蕩會向下游傳播,最終導致整個空泡失穩.圖11為實驗中通過高速攝影拍攝到的空泡內部液體回射流和空泡界面發生接觸,從而導致空泡失穩的過程,實驗條件對應仿真工況為L=0.6,J=0.68 .目前的數值仿真結果能很好地預測到這種空泡失穩機制,同時從可以不同時刻提取的空泡內液體回射流的位置,辨析出回射流向上游輸運的速率,大小接近于外部水流的一半.液體回射流使得空泡內部由透明狀轉變為水氣摻混的模糊狀態.并在向上游輸運的過程中與空泡界面碰撞,造成空泡界面波動.

圖10 液體回射流作用下空泡失穩過程Fig.10 Cavity instablity process under the liquid back-jet flow

圖11 實驗中拍攝液體回射流誘導空泡失穩過程Fig.11 Cavity instablity process under the liquid back-jet flow in the experiment

2.1.4 射流強度對空泡穩定性的影響

分析在空泡失穩的過程中,剪切和重力作用是主要因素,強剪切力使得空泡形態拉長夾斷.而空泡夾斷過程中往往伴隨著氣流的回擊現象,使得泡內壓力的突增和突降.圖12 展示了隨著射流強度的增加,通氣空泡形態的變化.當時,射流對空泡的泄氣作用,導致空泡形體相對于初始空泡,長度減小,尾部出現氣團脫落,但空泡界面保持穩定.當射流強度增加至時,液體沖擊界面進入空泡內,形成液體回射流.當射流進一步增強至空泡頸縮位置逐漸向噴管出口靠近,通氣空泡由自由閉合流型在射流作用下轉變為尾部閉合流型.當射流強度達到時,射流出口位置以前的空泡形態受到擾動發生變形.此時的空泡具有很強的瞬態特性,其形狀和尺寸較透明空泡隨時間變化更為劇烈.空泡尾部射流區摻混大量離散氣團和液滴/氣泡云,形態與純射流較為接近.

圖12 隨著射流強度增加,通氣空泡體積分數云圖Fig.12 Volume fraction cloud plot for the caity as the jet intensity increases

總的來說,射流強度越強,氣液兩側的剪切作用越強,產生的液體回射流的強度越大,界面越容易破壞,最終造成液體沖擊界面進入空泡內,形成液體回射流,進一步空泡界面會破碎,變成水氣摻混的狀態.

圖13 對比不同射流強度條件下空泡內壓力隨時間的變化Fig.13 The change of pressure inside the caivty with time is compared under different jet intensity conditions

圖13 對比不同射流強度條件下空泡內壓力隨時間的變化(續)Fig.13 The change of pressure inside the caivty with time is comparedunder different jet intensity conditions (continued)

2.2 不同模型長度計算結果分析

2.2.1 相對位置對空泡穩定性的影響

仿真計算過程中同時也對比了4 個不同的模型長度條件下空泡射流相互作用的結果.圖14 展示了隨著模型長度的增加,通氣空泡形態的變化.除了第一個工況空泡失穩以外,其他3 個工況,空泡都保持穩定狀態.原因是射流與空泡頭部相對距離越小,空泡內液體回射流越容易沖擊空泡頭部界面,導致空泡越容易失穩.

圖14 隨著模型長度增加,通氣空泡體積分數云圖Fig.14 Volume fraction cloud plot for the caity as the model length increases

圖15 對比不同模型長度條件下空泡內壓力隨時間的變化Fig.15 The change of pressure inside the caivty with time is compared under different model length conditions

特別注意的是當射流強度一定時,隨著模型長度的增加,液體回射流并沒有產生.分析原因為,模型長度越長,在空泡夾斷后空泡尾部越容易保持尖尾型.假定尾噴流作用下空泡橫截面仍然保持橢圓曲線,長半軸為 0.5(L+Lt),短半軸為Rmax,如圖16所示,其中Rmax代表空泡最大半徑,L為模型長度,Lt為噴管出口到空泡夾斷處的距離長度.從圖12 數值仿真的結果得到,Rmax近似相等.橢圓曲線在短半軸一致條件下,長半軸越長,曲線的曲率變化越小.即隨著模型長度的增加,空泡尾部的夾角傾向于減小,抑制液體回射流的形成.另外液體射流向前運動過程中,沿著模型壁面,動能存在一定的損耗,模型越長,液體射流到達空化器附近損耗的能量也越大,對空泡界面的影響也將減小.

圖16 尾噴流作用下空泡尺寸示意圖Fig.16 Sketch map of cavity size under the action of a tail jet

總的來說,模型長度越小,噴管出口離空化器越近,空泡內尾流擾動越容易傳播至空化器,界面的初始擾動也越大,界面越容易破壞.

2.2.2 射流作用下空泡穩定和失穩的臨界條件

通過上述分析可以得到空泡失穩機制主要取決于兩個無量綱參數為無量綱射流動量,數學形式為射流推力和空化器阻力之比,代表射流強度.為無量綱模型長度,數學形式為模型長度和空化器直徑之比,代表射流在通氣空泡內的的相對位置.越大,越小,空泡越容易失穩.在此基礎上,進一步總結了算例中出現穩定和失穩兩種狀態的臨界曲線,如圖17 所示.

圖17 射流作用下空泡穩定和失穩的臨界條件Fig.17 Critical conditions for the stable and unstable cavity under tail jet action

3 尾噴流作用下穩定空泡的閉合位置理論分析

射流在空泡內表現為受限射流,其卷吸效應的強度一定程度上受到空泡形態變化的影響.結合經典的射流動力學理論,對Paryshev 理論[14]推導過程中的連續方程加以合理修正,并考慮空泡內氣體和射流氣體之間的湍流擴散和卷吸效應帶來的射流速度衰減,構建空泡射流結構判別模型.射流作用下空泡內部質量流動和壓力分布如圖18 所示.Qj代表噴管出口射流流量,Q2,Q3.分別代表射流帶走和回流的流量.Wc代表空化器阻力.空泡截面面積變化可由獨立擴張原理[29]得到

其中,S0代表噴管出口面積,S1和S2分別代表空泡閉合處和閉合處下游附近空泡截面面積,S3代表射流回流截面面積(如圖18 所示).U0,U2,U3為對應位置處的速度.不考慮氣體可壓縮性,根據動量方程

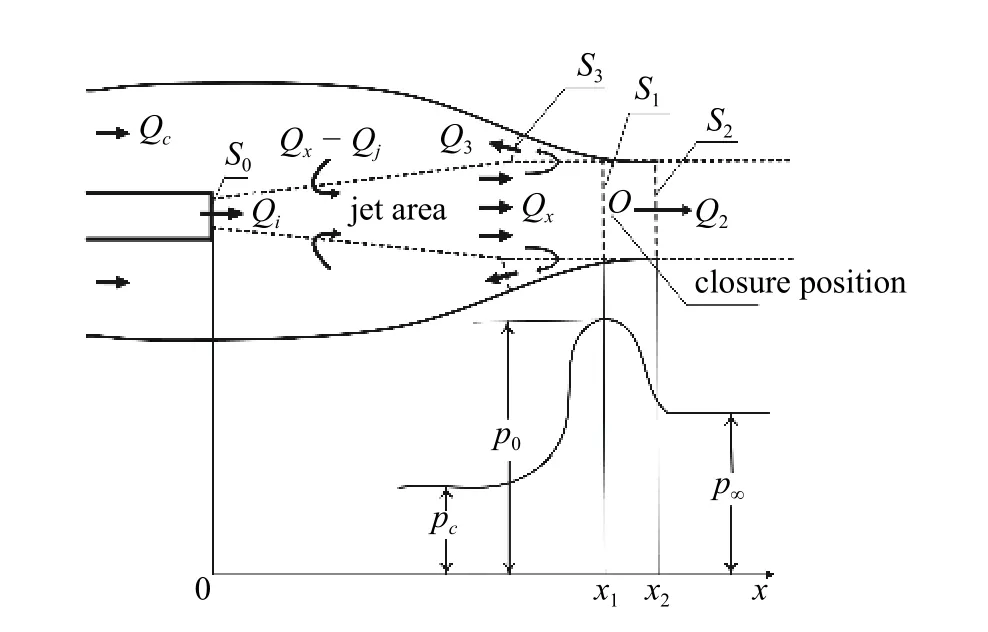
圖18 射流作用下空泡內部質量流動和壓力分布示意圖Fig.18 Schematic of the cavity internal mass flow and pressure distribution with a gasous jet

空泡穩定閉合以后,空泡流入和流出的氣體質量應該守恒(前提是射流作用下空泡為穩定狀態,因為一旦失穩,破碎界面帶來氣體損失不可忽視),而通氣的流量遠遠小于射流流量,可以忽略,得到連續方程,Qj=Q2,即

假定射流中心軸線速度衰減和射流卷吸周圍氣體流量都呈線性關系[30]

通過上面4 個方程式(22)～ 式(25),假設射流回流的速度大小近似等于射流在閉合點下游的速度,U3≈U2,并且空化數由此可以得到無量綱的回流流量為

根據空泡內部質量流量平衡,在空泡閉合處射流卷吸空泡內氣體流量應該等于射流的回流流量,即可得到尾噴射流作用下,空泡的理論閉合位置離噴管出口距離可表示為

對于射流作用下空泡穩定的工況,空泡尾部閉合位置到噴管出口的無量綱長度只與有關,與模型長度無關.此結論得到數值仿真和實驗結果支撐,如圖19 所示,不同模型長度條件下,空泡閉合位置到噴管出口長度,實驗和仿真結果對比誤差均在8%以內.在水洞中開展的驗證實驗,水洞中流速為5 m/s,模型采用頭部支撐方式.模型內設置兩路通道,一路在頭部空化器處通氣形成通氣空泡,一路在尾部通氣形成射流.

圖19 不同模型長度條件下空泡尾部閉合位置到噴管出口長度的實驗結果Fig.19 Experimental and numerical results on the length from the nozzle outlet to the closed position under differert model length

4 結論

本文利用VOF 耦合level set 界面追蹤方法,考慮氣體的可壓縮性,展開了一系列改變射流強度和模型長度的通氣空泡和超音速尾射流相互作用的數值仿真,重點分析了通氣空泡的穩定性和閉合位置.數值結果表明:

(1)在超音速尾射流作用下,通氣空泡的界面會經歷膨脹、頸縮、斷裂回縮過程,然后開始周期性震蕩泄氣.通氣空泡的形態長度相較于無射流條件下大大減小.

(2)空泡失穩過程中,空泡尾部產生液體回射流會順著氣體回流路徑向前沖擊空化器附近界面.其產生過程與空泡斷裂時尾部形態緊密聯系,并表現出上下不對稱的特點,更易形成于空泡尾部上表面.

(3)氣液界面兩側強剪切和重力作用誘導了液體射流的形成,而這種空泡失穩機制主要取決于兩個無量綱參數(射流推力和空化器阻力之比)和(模型長度和空化器直徑之比),越大,越小,空泡越容易失穩.在此基礎上,進一步總結了不同工況下出現穩定和失穩兩種狀態的臨界曲線.

(4)空泡越穩定,噴管出口的壓力波動的幅度和頻率就越低,通氣空泡能為火箭發動機提供穩定的工作環境.

(5)對于空泡失穩的工況,空泡閉合在噴管出口;而空泡穩定的工況,噴管出口到閉合位置的長度只與有關,與模型長度無關.