七人表決邏輯電路的設計與實現
孫宇舸,葉 檸,李景宏
(東北大學 信息科學與工程學院,遼寧 沈陽 110819)
表決邏輯在實際生活中具有廣泛的應用。如何設計表決邏輯電路是組合邏輯電路的重要研究內容。
在大部分表決邏輯電路的分析與設計中,通常都是以三人表決邏輯電路的設計[1-4]為例來說明組合邏輯電路的設計方法,很少涉及五人以上的表決邏輯電路的設計。因為當邏輯變量個數較多時,輸入輸出的邏輯關系以及邏輯函數的化簡和電路設計都比較復雜。但是在實際的生產和生活當中,多人表決邏輯具有廣泛的需求[5],本文就是以七人表決邏輯電路設計為例,說明多人表決邏輯的設計方法和電路實現。
本文主要研究了七變量的表決電路的邏輯關系,提出了簡易的七變量表決邏輯卡諾圖的化簡方法,將原本復雜而龐大的七變量卡諾圖分解為4個四變量卡諾圖,實現化繁為簡,從而得出七人表決邏輯的邏輯函數表達式,通過對邏輯函數表達式的分析與變換,通過數據選擇器進一步簡化電路,實現了七人表決邏輯電路的設計。
1 設計方法
表決邏輯電路是根據輸入狀態決定輸出狀態,因此屬于組合邏輯電路。組合邏輯電路的設計步驟[6]如圖1所示。
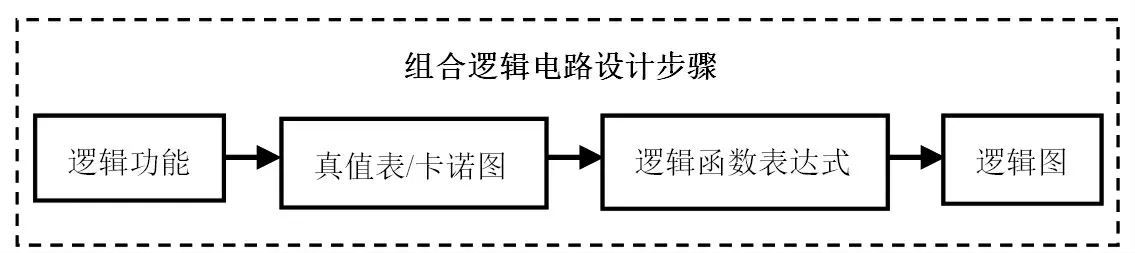
圖1 組合邏輯電路的設計步驟
1.1 基于邏輯功能的描述,分析事件的因果關系,確定電路的輸入邏輯變量和輸出邏輯變量
通常把事件的起因定義為輸入邏輯變量,事件的結果定義為輸出邏輯變量,并用二值邏輯的0和1對輸入和輸出變量進行邏輯賦值[5]。
七人表決邏輯的邏輯功能為:由七人投票決定決議是否通過。當多數人投票同意時,即同意人數大于等于4人時,表示決議通過;當同意人數小于4人時,表示決議不被通過。因此該電路輸入變量為7個,即參與投票的7人,分別用字母A、B、C、D、E、F、G表示,“同意”定義為1,“不同意”定義為0。輸出變量表示決議是否被通過,用字母Y表示,“通過”定義為1,“不通過”定義為0。
1.2 由文字描述的邏輯功能的因果關系,列出真值表或卡諾圖
卡諾圖(Karnaugh map)是數字邏輯電路設計中的一種常用數學工具,是邏輯函數的一種圖形化表示方法,和真值表一樣可以表示邏輯函數和輸入邏輯變量之間的邏輯關系,與真值表具有一一對應的關系,可以看做是真值表的一種變形。畫卡諾圖時,需要注意要將邏輯上相鄰的最小項變成幾何位置上相鄰的方格圖,做到邏輯相鄰和幾何相鄰的一致性[6]。
在七人表決邏輯中,由于輸入變量為7個,因此輸入變量的取值組合一共有27=128種,可見無論是七變量的真值表還是卡諾圖都會相當復雜,因此本文針對表決邏輯,提出一種將七變量卡諾圖轉換為4個四變量卡諾圖的方法。
將三個輸入變量E、F、G單獨考慮,則可以將七人表決邏輯功能分為四種情況:
(1)當EFG三個變量都為0時,即EFG=000,則A、B、C、D四個變量都為1時,輸出Y=1,其他取值組合輸出Y=0,對應的卡諾圖如圖2所示。
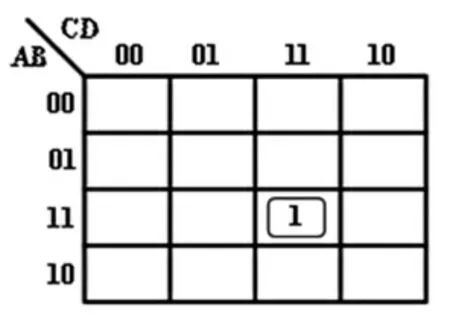
圖2 七人表決邏輯卡諾圖(EFG=000)
(2)當EFG三個變量中有一個變量為1時,即EFG=001/010/100時,則A、B、C、D四個變量中至少有三個變量為1時,輸出Y=1,其他取值組合輸出Y=0,對應的卡諾圖如圖3所示。
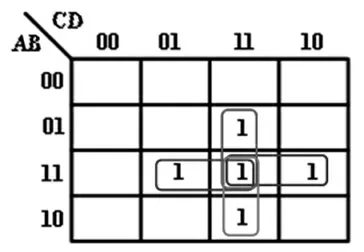
圖3 七人表決邏輯卡諾圖(EFG=001/010/100)
(3)當EFG三個變量中有兩個變量為1時,即EFG=011/101/110,則A、B、C、D四個變量至少有兩個變量為1時,輸出Y=1,其他取值組合輸出Y=0,對應的卡諾圖如圖4所示。

圖4 七人表決邏輯卡諾圖(EFG=011/101/110)
(4)當EFG三個變量都為1時,即EFG=111時,則A、B、C、D四個變量中至少有一個變量為1時,輸出Y=1,其他取值組合輸出Y=0,對應的卡諾圖如圖5所示。
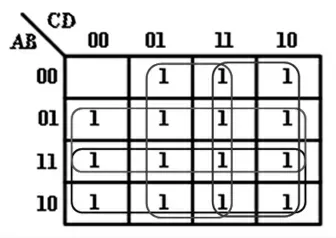
圖5 七人表決邏輯卡諾圖(EFG=111)
1.3 化簡卡諾圖,獲得最簡邏輯函數表達式
由于卡諾圖用幾何位置的相鄰表示了構成函數的各個最小項在邏輯上的相鄰性,因此可以方便地求出邏輯函數的最簡與或式,進而實現邏輯電路。
卡諾圖化簡邏輯函數的基本原則[7]為:
(1)圈1方格得邏輯原函數,圈0方格得邏輯反函數。
(2)包圍圈必須覆蓋所有的1方格。
(3)包圍圈中1的個數必須是2n個相鄰的1。
(4)包圍圈的個數必須最少(乘積項最少)。
(5)包圍圈越大越好(消去的變量多)。
(6)每個包圍圈至少包含一個新的最小項。
根據上述原則,分別對圖2-圖5的卡諾圖進行化簡,具體的包圍圈的畫法如圖中所示:
(1)當EFG三個變量都為0時,化簡圖2卡諾圖的包圍圈,得邏輯函數表達式為:

(2)當EFG三個變量中有一個變量為1時,化簡圖3卡諾圖的包圍圈,得邏輯函數表達式為:

(ABC+ABD+ACD+BCD)(E'F'G+E'FG'+EF'G')。
(3)當EFG三個變量中有兩個變量為1時,化簡圖4卡諾圖的包圍圈,得邏輯函數表達式為:
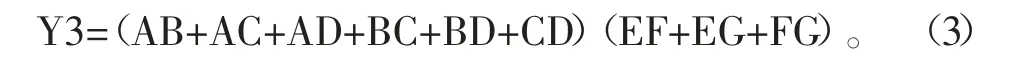
(4)當EFG三個變量都為1時,化簡圖5卡諾圖的包圍圈,得邏輯函數表達式為:
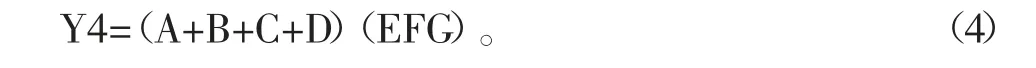
綜上所述,則七人表決邏輯的最簡邏輯函數的與或表達式為:

基于七人表決邏輯的邏輯功能描述,當大于等于4人同意時,決議通過,按照排列組合的方法可以確定一共有C74=35種組合,在邏輯函數表達式(5)中,邏輯函數為35個與項的或,與分析一致。
1.4 由化簡后的邏輯函數表達式畫出邏輯圖
邏輯圖是利用邏輯門來完成邏輯功能的電路圖。基于邏輯函數表達式(5),利用35個8輸入與門,4個8輸入或門,1個3輸入或門和1個5輸入或門即可實現七人表決邏輯的邏輯函數,基于基本邏輯門的七人表決邏輯的邏輯圖如圖6所示。
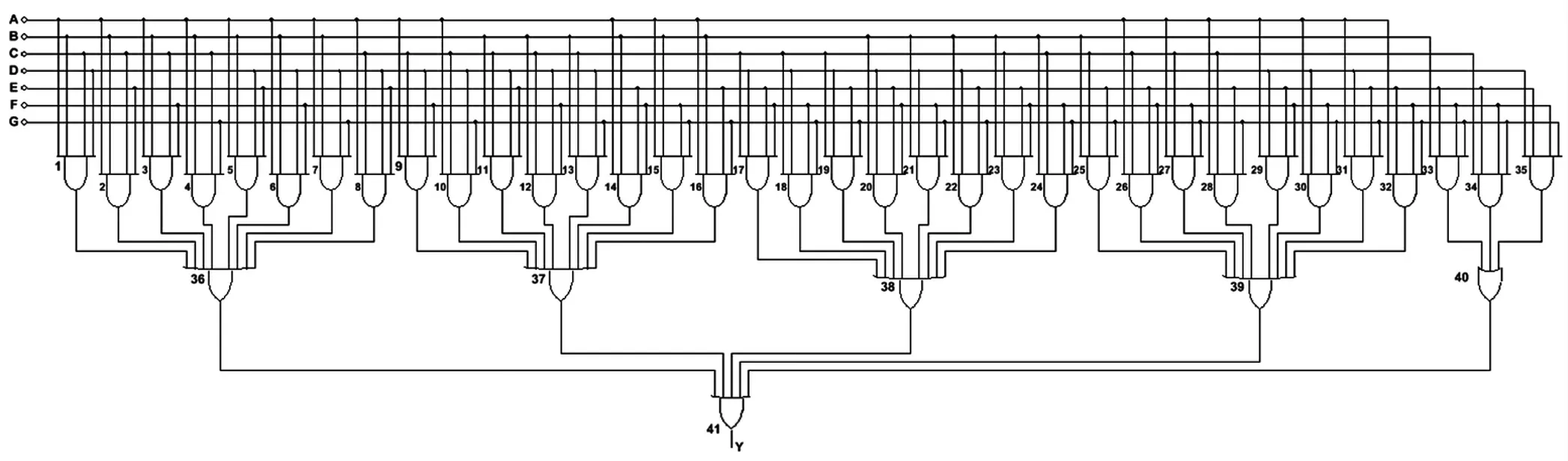
圖6 基于基本邏輯門的七人表決邏輯的邏輯圖
2 基于數據選擇器的電路設計與實現
由圖6可以看出,基于基本邏輯門實現的七人表決邏輯電路需要使用41個不同輸入變量的基本邏輯門,邏輯門數量眾多,電路復雜,可考慮進一步對電路進行簡化。
邏輯函數表達式(5)可以改寫為:

+(A+B+C+D+C)EFG。
根據八選一數據選擇器的邏輯函數:
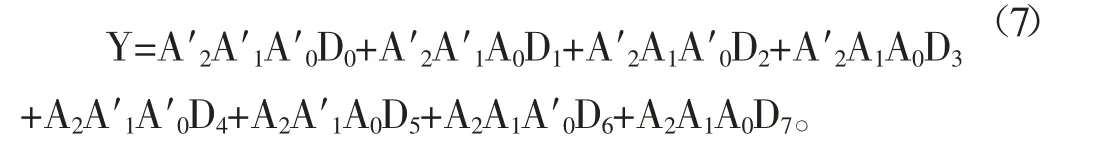
將EFG三個變量看做八選一數據選擇器的地址輸入端A2A1A0,則有:
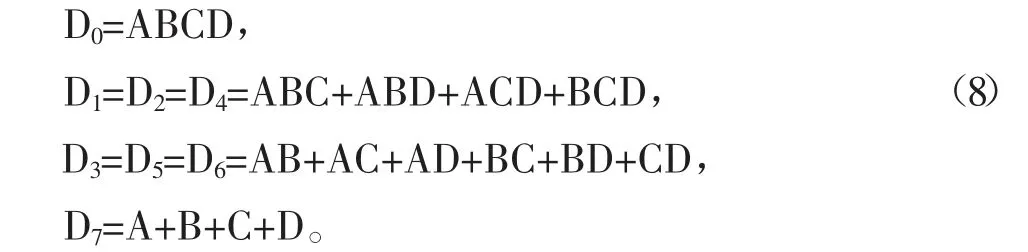
由此基于八選一數據選擇器74LS151實現的七人表決邏輯電路的電路圖如圖7所示。

圖7 基于數據選擇器的七人表決邏輯電路圖
采用數據選擇器將大大減少基本邏輯門的數量,大大簡化了電路結構,使電路更為穩定并具有一定的可擴展性。
3 結束語
本文研究了數字邏輯電路中的七人表決邏輯電路的設計方法,提出了基于表決邏輯的多變量卡諾圖的化簡方法,分別采用基本邏輯門電路和數據選擇器兩種方式實現了七人表決邏輯電路。文章的研究方法可向多變量表決邏輯電路擴展,為組合邏輯電路的分析與設計提供了新思路。

