改進的截斷核范數及在視頻前背景分離中的應用

2021-10-17 08:15:54楊永鵬楊真真李建林

工程科學與技術 2021年5期

楊永鵬，楊真真，李建林，范露

(1.南京信息職業技術學院網絡與通信學院，江蘇南京 210023；2.南京郵電大學寬帶無線通信與傳感網技術教育部重點實驗室，江蘇南京 210023)

視頻前背景分離一直是計算機視覺等領域研究的熱點，但是由于自然界存在的噪聲、模糊、遮擋和光照變化等的干擾，使其成為最具有挑戰性的問題之一。在此背景下，如何根據視頻先驗信息，構造魯棒性強、復雜度低的視頻前背景分離方案是其關鍵難題。魯棒主成分分析（robust principal component analysis，RPCA）[1]作為多媒體信息處理領域的前沿技術，被廣泛應用于視頻前背景分離[2–5]中，同時，也是視頻去噪[6]和人臉陰影移除[7]等領域的關鍵技術。傳統RPCA是一種將觀測矩陣分解為低秩矩陣和稀疏矩陣的方法，所以又被稱為稀疏低秩分解（sparse and low-rank decomposition，SLRD）。但是，由于該問題的非凸、非連續性等特點使傳統RPCA問題難以直接求解，且其是NP–難問題。為了求解該問題，主成分追蹤（principal component pursuit，PCP）算法[8]被提出，該算法分別采用核范數和L1范數替代傳統RPCA模型中的秩函數和L0范數。PCP算法能夠較好地解決多媒體信息處理領域中的諸多問題[8]，尤其是推動了視頻前背景分離[9]、矩陣填充[10]等技術領域的發展，并逐漸成為引領RPCA方法發展的基礎框架。但PCP算法也存在諸如時間復雜度高，平等對待所有奇異值，不能較好逼近秩函數和L0范數，抗噪聲能力弱以及不考慮結構化、運動化信息等缺陷。針對PCP算法存在的以上問題，改進的RPCA算法被提出并被應用于視頻前背景分離。

改進的算法主要分為凸替代RPCA方法、非凸替代RPCA方法、加入輔助信息的RPCA方法以及截斷核范數方法。例如，去分解（go decomposition，GoDec）算法[11]是一種經典的凸替代RPCA方法，它將受環境污染的觀測矩陣分解為低秩、稀疏和噪聲矩陣，增強了PCP算法的魯棒性，同時，采用雙邊隨機預測（bilateral random projections，BRP）方法[11]優化算法時間復雜度，提高算法收斂速度，但是，凸替代方法對秩函數和稀疏度函數的逼近程度不高，效果欠佳。在此基礎上，一系列非凸替代RPCA方法被陸續提出，例如，非凸非光滑加權核范數（nonconvex nonsmooth weighted nuclear norm，NNWNN）算法[12]、非凸低秩稀疏分解（nonconvex low-rank and sparse decomposition，NonLRSD）算法[13]、非凸秩逼近（nonconvex rank approximation，NRA）算法[14]、廣義雙步長（general dual step-size，GDSS）算法[15]、線性分類非凸（linear spectral clustering and non-convex，LSCNC）算法[16]、帶有分割稀疏的非凸RPCA（non-convex and segmentation constraint，NCSC）算法[17]、核化的非凸全變差RPCA（nonconvex total variation regularized RPCA with kernelization，KRPCA–NTV）算法[18]等，這些非凸替代RPCA方法采用較為先進的非凸替代函數替換傳統RPCA中的秩函數和稀疏度函數。但是，由于該類算法的替代函數仍然非最優，同時，容易忽略視頻中的結構化信息，使得視頻前背景分離的效果差強人意。考慮到視頻中存在大量的時空信息，于是許多基于輔助信息的RPCA方法被提出并應用于視頻前背景分離中，例如：基于低秩和結構化的稀疏分解（lowrank and structured sparse decomposition，LSD）算法[19]采用結構化稀疏誘導范數描述矩陣的稀疏成分，并將空間信息引入到RPCA算法模型中；基于運動信息輔助的矩陣恢復（motion-assisted matrix restoration，MAMR）算法[20]將運動信息引入到傳統RPCA模型中，輔助信息的加入促進了矩陣分解的準確性，尤其對受光照變化、水紋波動等影響的觀測矩陣分解效果明顯。但是，該類算法較難描述視頻中的輔助信息，視頻前背景分離效果不穩定，同時，由于大量輔助信息計算的引入導致算法時間復雜度較高，視頻前背景分離的時間較長。

截斷核范數（truncated nuclear norm，TNN）算法[21–23]是為了解決PCP算法中核范數平等對待所有奇異值的問題而提出的一種更逼近秩函數的方法。與傳統RPCA不同的是，TNN算法是對 min(m,n)?r個奇異值進行最優化計算，并最終將傳統RPCA模型轉換為一個凸優化問題進行求解。通過大量的理論論證和實驗驗證表明TNN能夠取得較好的視頻前背景分離效果。在TNN算法的基礎上，諸多改進的TNN算法陸續被提出并廣泛應用于視頻前背景分離中，例如，Hu等[21]提出了一種基于截斷核范數和稀疏正則化（truncated nuclear norm and a sparse regularizer，TNNSR）的低秩稀疏分解算法，該算法在TNN的基礎上增加了稀疏先驗項，提高了TNN算法的魯棒性。雖然大量實驗表明TNN及其改進算法在視頻前背景分離中具有較好的效果，但是由于TNN模型中的核范數仍然是凸替代函數，逼近程度弱，算法效果欠優，仍然亟待改進。

本文提出了一種改進的截斷核范數（improved truncated nuclear norm，ITNN）算法，為了增強TNN算法對傳統RPCA算法的逼近度，該算法采用非凸γ范數替代TNN算法中的核范數，并從理論上分析了非凸γ范數比核范數逼近度更高的原因。同時，本文采用廣義交替方向乘子法（generalized alternating direction method of multipliers，GADMM）[24–25]求解ITNN算法模型。最后，將ITNN算法及其對比算法應用到視頻前背景分離實驗中，驗證ITNN算法的有效和優越性。

1 改進的截斷核范數

1.1 改進的截斷核范數的模型

鑒于矩陣M的秩與其較小的 min(m,n)?r個非零奇異值相關，TNN算法將傳統的RPCA模型轉換為如式（1）所示的模型：

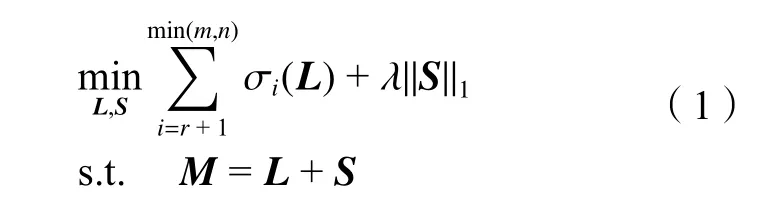
式中，M∈Rm×n為已知的觀測矩陣，L∈Rm×n為低秩矩陣，S∈Rm×n為稀疏矩陣，σi(L)為矩陣L的奇異值，r為截斷的奇異值個數。

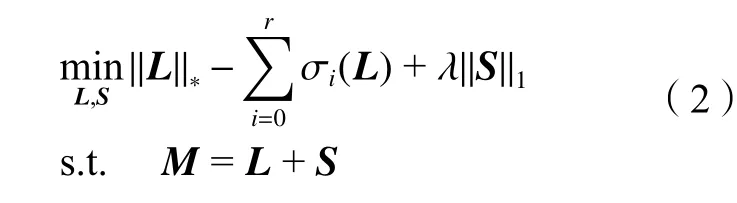
由文獻[21]可知，式（2）可以轉換為如下問題：

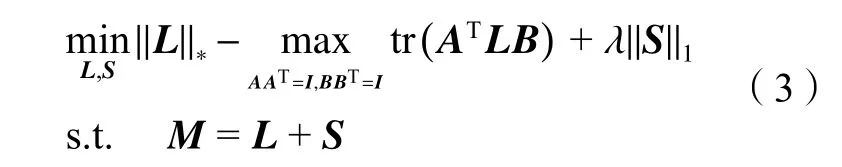
式中：A=(u1,u2,···,ur)∈Rm×r為低秩矩陣L的前r個左奇異向量；B=(v1,v2,···,vr)∈Rn×r為低秩矩陣L的前r個右奇異向量；核范數 //L//?為秩函數的凸有偏估計，其對秩函數的逼近程度低。研究表明非凸替代函數能更好地逼近傳統RPCA模型中的秩函數[12–18]。本文采用非凸γ范數[14]替代TNN算法中的核范數，γ范數的表達式如下：

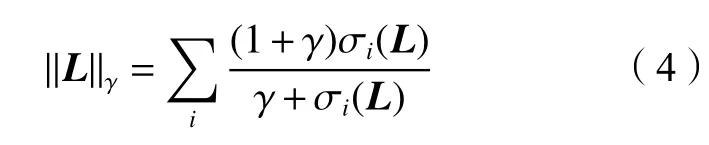
式中，i=1,2,···,min(m,n)。又因為：

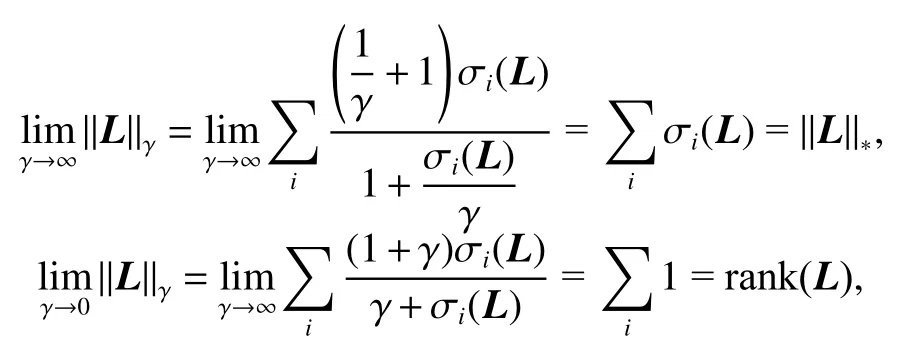
所以，γ范數比核范數更逼近秩函數。另外，為了進一步說明γ范數的逼近度，本文給出了γ 范數（γ=0.1, 0.01）和核范數的函數圖形，如圖1所示。從圖1可以看到，本文提出的γ范數比核范數更逼近秩函數，同時， γ=0.01的逼近效果比 γ =0.1更好，本實驗中所用的 γ =0.01。

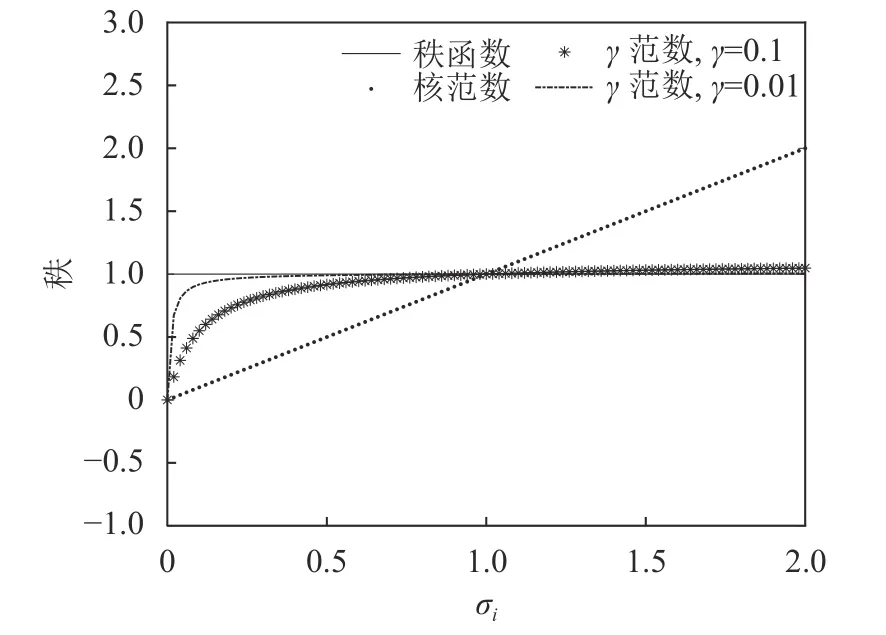
圖1 不同范數逼近秩函數的對比Fig. 1 Comparison of different norms approximating to the rank function

于是，本文提出ITNN模型如下：

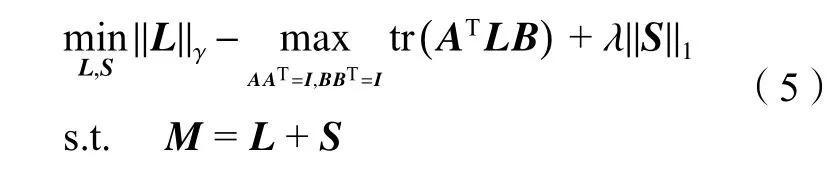
1.2 改進的截斷核范數模型求解

步驟1：給定Lk對Lk進行奇異值分解即[Uk,Σk,Vk]=S VD(Lk) ，得到Lk對應的左、右奇異向量如下：

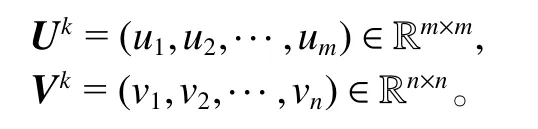
并通過取對應的前r個左、右奇異向量得到：

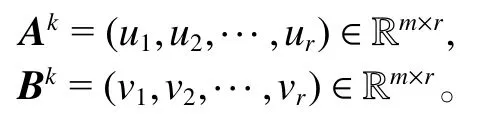
步驟2：在步驟1的基礎上求解優化問題：

本文采用GADMM算法求解式（6）所示的優化問題，其對應的增廣拉格朗日函數為：

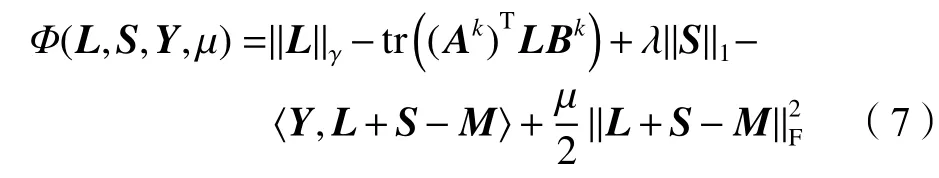
式中，Y為拉格朗日乘子， μ＞0 為懲罰參數， // ·//F是Frobenius范數。通過以下步驟對問題（6）進行求解：

首先，固定St、Yt和μt，更新Lt+1，即

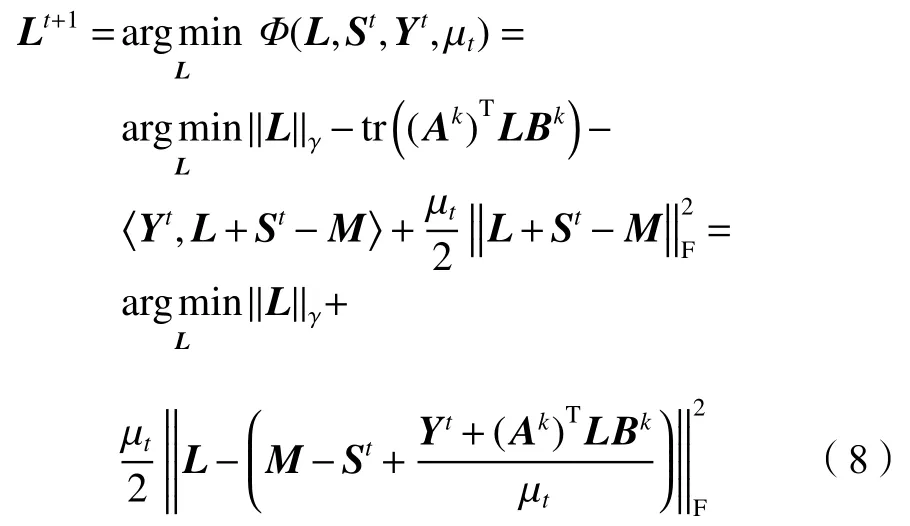
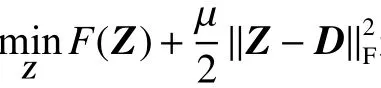
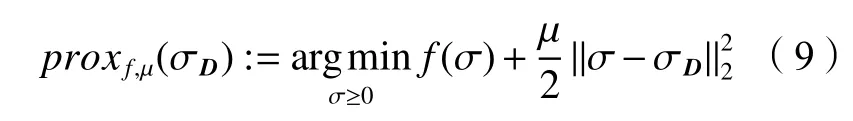
式（9）可以用凸規劃差分（difference of convex，DC）算法[14]進行求解。

于是，得到式（8）的最優解為：

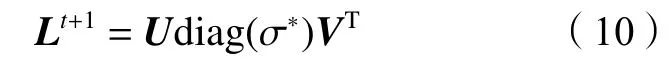
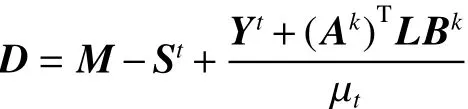
其次，固定Lt+1、Yt和μt，更新變量St+1，即

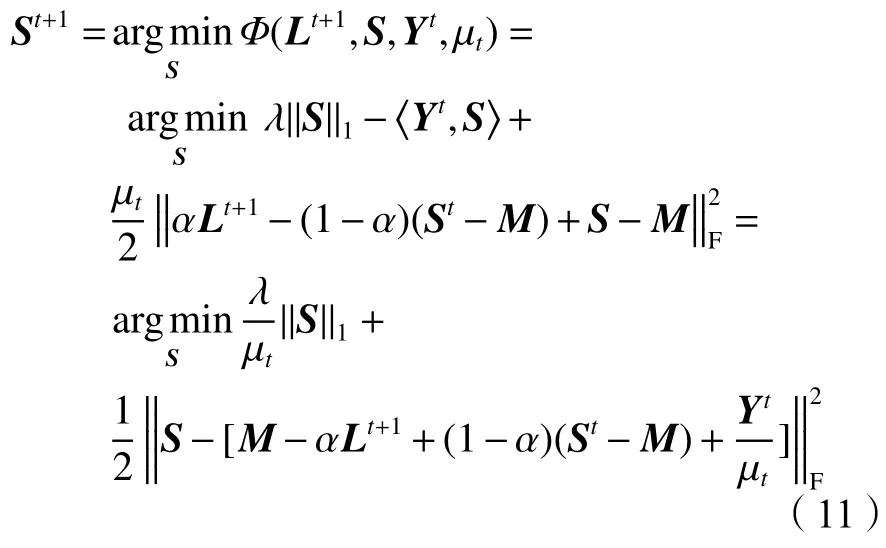
式中， α∈(0,2) 為松弛因子。當 α=1時，GADMM算法退化為經典的ADMM算法。可以利用軟閾值收縮算子對式（11）的變量St+1進行更新，得到迭代格式如下：

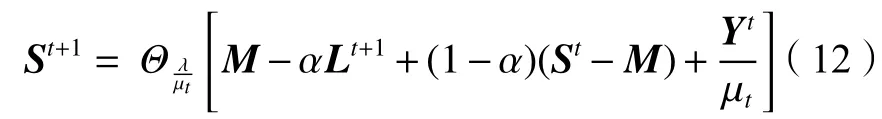
式中， Θξ(·) 為軟閾值收縮算子，定義為Θξ(E)=max(|E|?ξ,0)·sign(E)，其中，ξ ＞0 為參數，s ign(·)為符號函數。

最后，固定Lt+1、St+1，更新拉格朗日乘子Yt+1和懲罰因子μt+1：

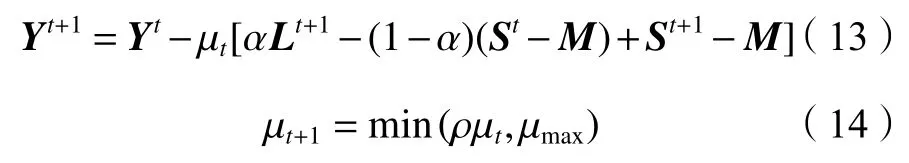
式中，ρ為放大系數。

綜上所述，使用算法1、2求解問題（5）。

算法1求解問題（5）的總算法

1）初始化：L0=0。

2）給定Lk，計算Lk的奇異值分解：

[Uk,Σk,Vk]=S VD(Lk),

得到左、右奇異向量Uk和Vk，進而得到其分別對應的截斷奇異向量Ak和Bk。

3）求解如下優化問題：

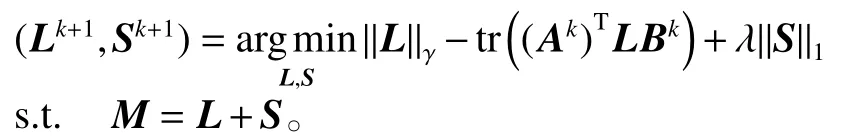
下面給出采用GADMM算法求解算法1中步驟3）（問題（6））的具體算法2，。

算法2采用GADMM求解算法1中步驟3）的算法

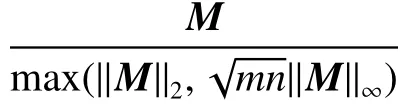
2）根據式（10）更新變量Lt+1。

3）根據式（12）更新變量St+1。

4）根據式（13）更新Yt+1。

5）根據式（14）更新 μt+1。

2 實驗結果與分析

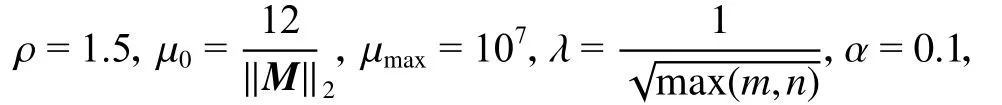
為了驗證提出的ITNN算法的優勢，以8個實驗視頻序列為實驗對象，進行視頻前背景分離仿真實驗，并隨機選取Airport視頻的第1 656幀、ShoppingMall視頻的第1 862幀、WaterSurface視頻的第1 624幀、Escalator視頻的第4 595幀、Curtain視頻的第22 774幀、Cubicle視頻的第1 303幀、Corridor視頻的第817幀和Car視頻的第689幀的實驗效果進行分析，實驗結果如圖2所示。

圖2 各算法提取的視頻前景對比Fig. 2 Comparison of video foreground extracted by different methods

從圖2可以看出：本文提出的ITNN算法較其他對比算法具有更好的分離效果。例如：從Airport視頻提取前景的效果（圖2的第1行）可以看出，本文提出的ITNN算法提取的前景圖片的中間偏右部分和中間偏上部分比其他對比算法的噪聲更少。從對Shopping-Mall視頻提取前景的效果（圖2的第2行）可以看出，ITNN算法提取的前景的右上角部分具有較少的噪聲。從WaterSurface視頻提取前景的效果（圖2的第3行）可以看出，ITNN算法從視頻中提取的人的輪廓信息更加豐富和完整，噪聲更少；同等條件下，其他算法只能提取人輪廓的一半乃至更少的信息，且提取的前景所包含的噪聲較多，產生噪聲最明顯的是Godec算法。從Curtain視頻提取前景的效果（圖2的第5行）可以看出，ITNN算法提取的前景中人的信息較豐富，尤其是比TNN算法提取的人的信息豐富，并且比GDSS、MAMR、NNWNN、NonLRSD、Godec和PCP算法產生的噪聲更少。綜上所述，從視覺角度來看，本文提出的ITNN算法與其他對比算法相比提取的前景效果更好，前景信息更豐富和完整。

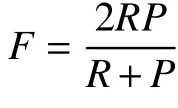
ITNN算法與上述7種對比算法進行視頻前背景分離的F-measure值如表1所示。表1的最后一行給出了每種算法在視頻前背景分離過程中的平均F-measure值。

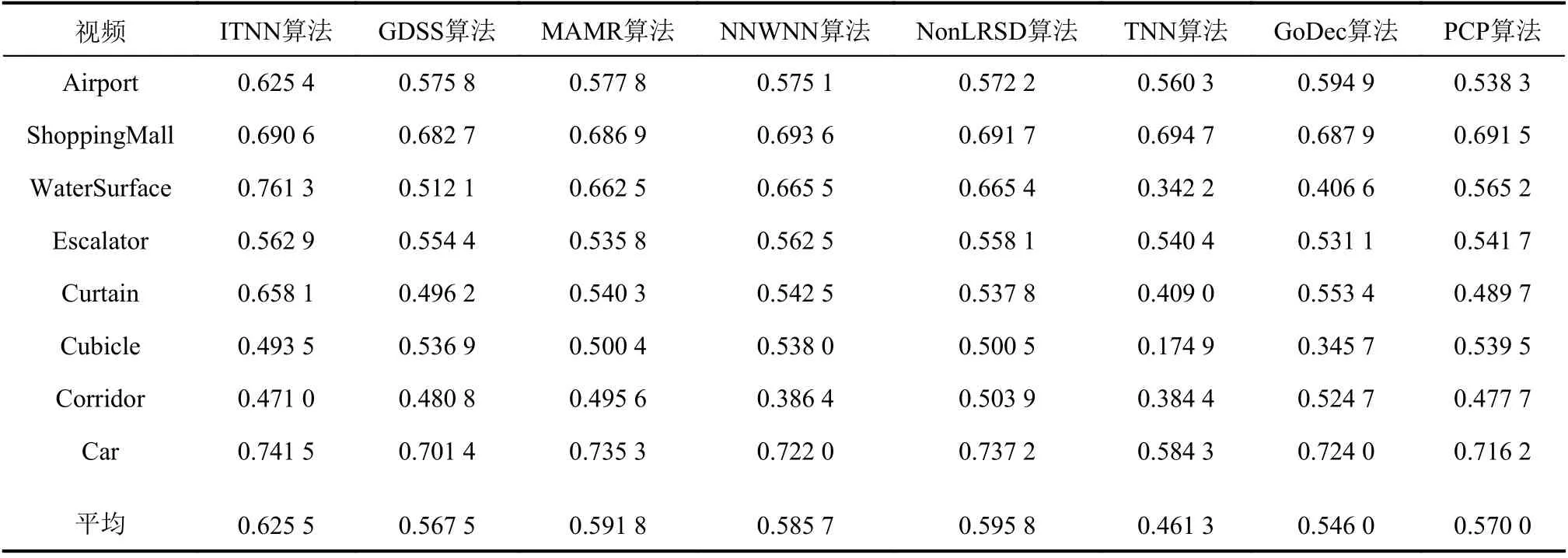
表1 不同算法的視頻前背景分離的F-measure值Tab. 1 F-measure of different methods in the experiments of foreground-background separation

從表1可以看出：ITNN算法在對Airport、Water-Surface、Escalator、Curtain和Car進行視頻前背景分離的F-measure值較其他對比算法更高。例如，對Airport視頻，ITNN算法的F-measure值比PCP算法高9%；對WaterSurface視頻，ITNN算法的F-measure值比TNN算法高42%；對Escalator視頻，ITNN算法的F-measure值比Godec算法高3%；對Curtain視頻，ITNN算法的F-measure值比Godec算法高12%；對Car視頻，ITNN算法的F-measure值比TNN算法高12%。平均F-measure值最高的為本文提出的ITNN算法，比次高的NonLRSD算法高3%，比最低的TNN算法高12%，也即本文提出的ITNN算法比其他7種基于RPCA的視頻前背景分離算法的效果更好，從而定量地驗證了提出的ITNN算法的優越性。

為了驗證ITNN算法的時間復雜度，實驗記錄了ITNN算法與上述7種對比算法進行視頻的前背景分離的運行時間，如表2所示。

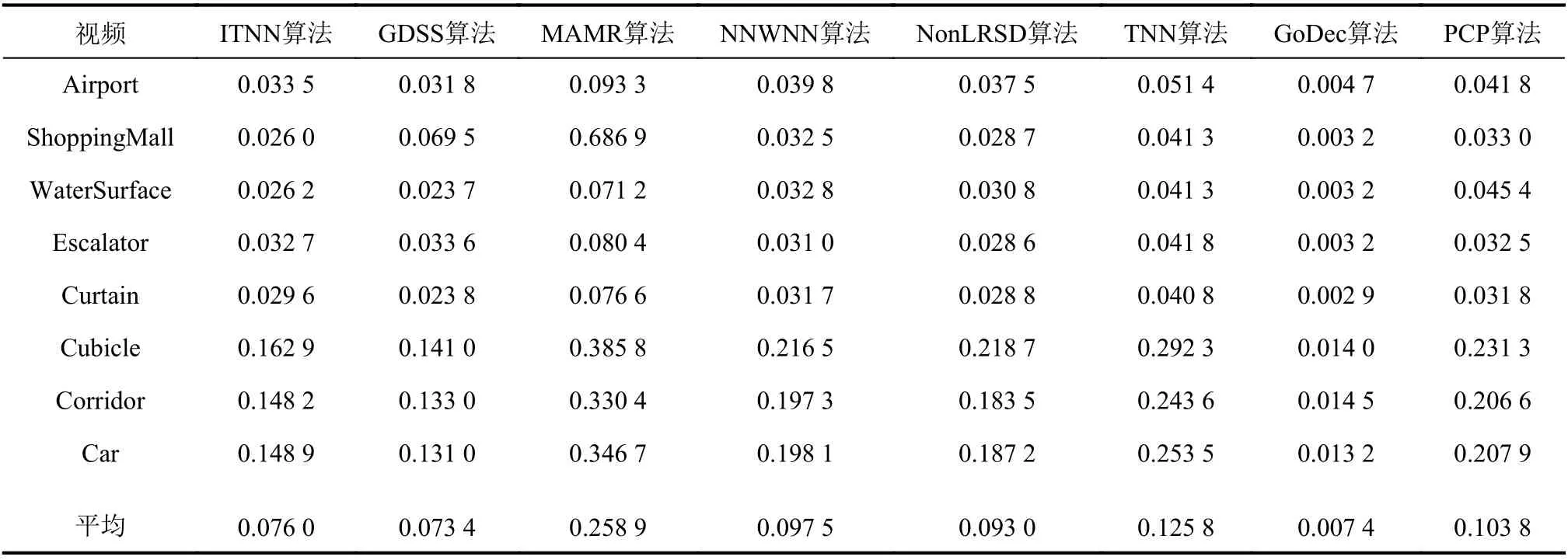
表2 不同算法的視頻前背景分離運行時間比較Tab. 2 Comparison of running time of each algorithm in the foreground-background separation s/幀

從表2中的平均時間可以看出：由于GoDec算法使用了加速算法，所以其運行時間最快；除GoDec算法外，ITNN算法的平均運行時間只比GDSS算法略慢，但比其他5種算法要快，其中，比MAMR算法快0.18 s/幀，比NNWNN算法快0.02 s/幀，比NonLRSD算法快0.017 s/幀，比TNN算法快0.5 s/幀，比PCP算法快0.3 s/幀。進一步驗證了ITNN算法在時間復雜度上的優勢。

綜上所述，本文從視覺和量化（即F-measure值和運行時間）兩個角度驗證了提出的ITNN算法的優越性。

3 結論