基于動作基元的擬人機械臂仿人運動規劃

衛 沅

(河南科技大學 車輛與交通工程學院，河南 洛陽 471000)

人類作為自然界長期進化的高等生物，在結構和功能上有著許多獨特的優越性，如人臂的安全性、柔順性、運動靈活性等。把人體的相關特性應用到機器人的研究中，不僅可以使機器人的結構和功能產生質的飛躍，還可以幫助仿人機器人更好地融入人類社會生活并與人類進行高效、友好的溝通協作[1]。擬人機械臂的仿人運動研究在仿人機器人中占有重要的地位，它的技術成熟與否直接決定機器人能否勝任復雜而精細的操作任務[2]。

目前，對于擬人臂仿人運動規劃的研究大致可以分為兩類：一類是基于指標的方法，建立人臂臂姿指標，通過對指標的優化來達到目的。其中，應用較廣的是由心理物理學演化而來的不舒適度指標[3]，該指標表明當關節角越遠離中心角時，人就越感到不舒適。除此之外，學者們通過建立其他不同類型的指標來進行擬人臂的仿人運動。Zhao等[4]提出了一種基于能量指標的方法來進行臂姿的預測，該能量指標包括重力勢能和彈性勢能。甘亞輝等[5]利用人體工程學中的快速上肢評價指標來選定符合人類操作特點且滿足性能要求的擬人臂構型。一些學者采用多目標函數融合的方式進行臂姿的預測。Chevtchenko等[6]在不舒適度指標的基礎上，融合了關節位移、勢能變化等其他指標，利用多指標加權的方式進行運動的預測。另一類是基于特性的方法，提取人臂運動特性，并將其融入到仿人運動規劃中。這一類方法主要以人臂的某些特殊運動為研究對象，通過成千上百次的實驗數據采集，利用如回歸模型等數據算法對實驗數據進行整合分析，歸納出人臂運動模型并使機械臂自主生成仿人運動[7]。其中，應用較為普遍的是肘部旋轉角及其演化算法，通過建立人臂三角形實現擬人臂的仿人運動[8]。

無論是基于指標還是基于特性的方法，都存在不可避免的缺陷。在基于指標的研究中，單一指標往往不能滿足仿人運動的需要，而多指標體系由于權重系數的影響，又存在很多不確定性。在基于特性的研究中，盡管有很多方法能夠提取人臂臂姿特性，但是這些特性的準確性還有待進一步的驗證。此外，這些特性大部分只是人臂所呈現出的表面現象，并不能反映人臂運動的真正內在機理。隨著計算機技術及人工智能技術的發展，越來越多的新穎算法被應用到擬人臂的仿人運動中，例如，神經網絡算法、貝葉斯網絡算法等[9–10]。盡管這些算法能夠幫助擬人臂產生類人化的手臂運動，但是往往忽略了手臂模型對運動精度的影響。人類的手臂運動是十分復雜的，運動過程中手臂的狀態并不是一成不變的，不同的關節數和關節組合構成了不同的運動狀態[11–12]。

針對人臂運動相似性及多樣性特點[13]，作者提出一種基于動作基元的人臂運動表達方式，能夠直觀反映人臂運動的內在機理。運動模型的多樣化也能降低權重系數對整個運動精度的影響。此外，不同于傳統動作基元基于某種特定任務的建立模式，該表達方式可以涵蓋人臂的各種運動。同時，動作基元的特點可以有效、直接地建立人臂運動與擬人臂仿人運動之間的映射關系。根據不同基元的特點，建立對應的反解算法，使擬人臂能夠滿足仿人運動的要求。

1 手臂運動特點及運動學模型

人臂運動主要依靠關節，其結構由上至下依次由肩關節、肘關節和腕關節連接而成。其主要運動方式為肩部的外展/內收、彎曲/伸展和肱骨的旋轉、肘部的彎曲/伸展，以及小臂的旋前/旋后、腕部的外展/內收和腕部的彎曲/伸展。

采用的擬人臂實驗平臺為人形機器人NAO。NAO的每只手臂具有5個自由度，其中，肩關節3自由度，肘關節1自由度，腕關節1自由度，明確的生理關節配置使其可以應用到仿人運動規劃中。

如圖1所示，以右臂為例，采用D–H參數[14]描述擬人臂連桿之間的關系。

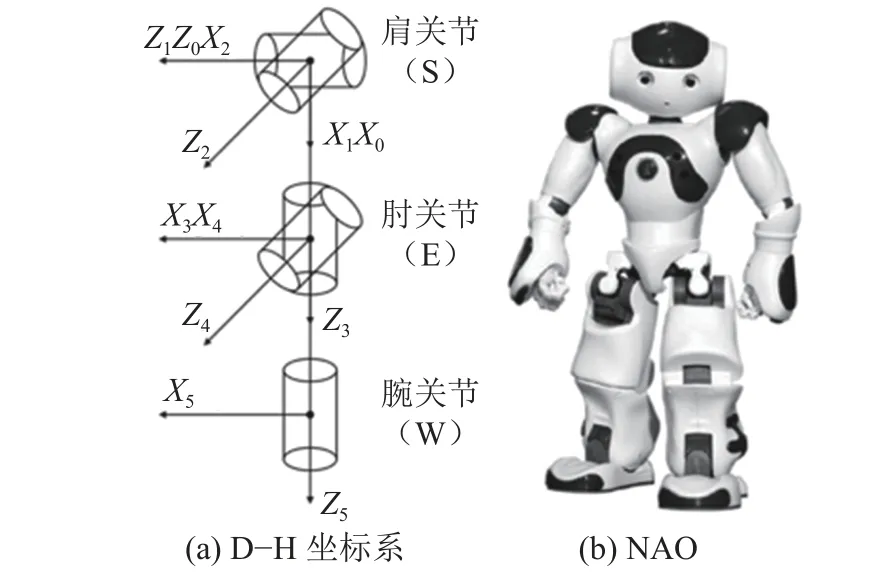
圖1 D–H坐標系和人形機器人NAOFig. 1 D–H coordinate and humanoid robot NAO

D–H參數如表1所示，其中，nu、nl、nh分別表示NAO大臂、小臂以及手掌的長度。

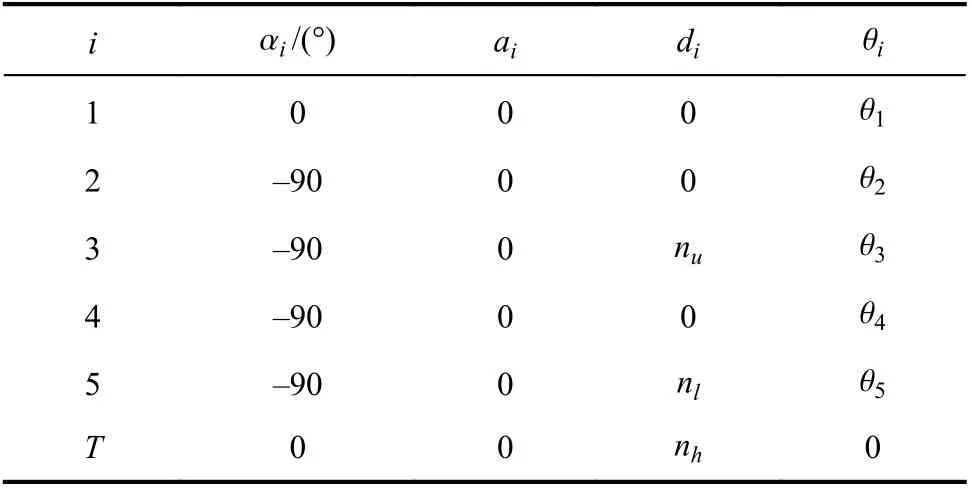
表1 NAO手臂D–H參數Tab. 1 D–H parameters of the NAO arm

2 基于動作基元的運動表達

神經生理學研究表明：脊椎動物和無脊椎動物的運動都是由動作基元組成的[15]。通過動作基元的排列與重組完成運動的表達與實現。目前在機器人領域，動作基元也得到了廣泛的應用。最主要的兩個特點是減少計算量和模塊化思想。特別是冗余度機器人，在智能學習及運動構成等方面有明顯的優勢[16]。

2.1 核心動作基元庫

人體結構可以以生理關節為基本單位，通過樹狀圖的形式描述。如圖1（a）所示，S、E、W3個節點分別表示人臂生理關節中的肩關節（父節點Parent）、肘關節（子節點Child）和腕關節（子孫節點Descendant）。根據人臂運動特點，每一個節點擁有兩種屬性：姿態屬性（R）和位置屬性（P）。姿態屬性表示生理關節姿態的變化；位置屬性表示生理關節位置的變化。圖2為節點屬性的詳細信息。本文基于各個生理關節的屬性，設定5種核心動作元素：SR、EP、ER、WP、WR。這5種動作元素分別對應了不同生理關節的不同屬性變化，如SR表示肩關節姿態屬性的變化，EP表示肘關節位置屬性的變化。

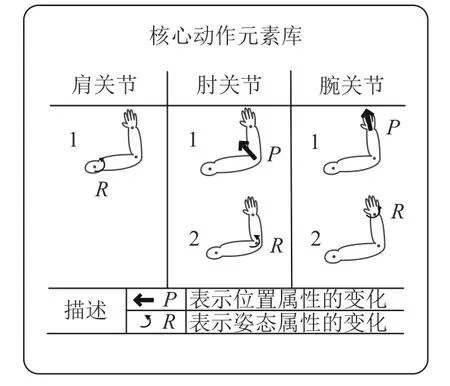
圖2 各關節屬性示意圖Fig. 2 Attributes of different joints

2.2 動作基元的提取法則

根據手臂節點屬性，驅動關節會發生姿態改變，并引起下層從動關節位置屬性的變化，而從動關節的位置屬性并不會主動改變。具體的提取法則如下：

1）父節點（S）固定在坐標系原點，其位置不會發生變化，因此肩關節只有姿態屬性會發生變化。

2）姿態屬性的變化是相對于父節點的，而位置屬性的變化是相對于世界坐標系的。

3）通常，父節點姿態屬性的變化會引起子節點位置屬性的變化，即：

ParentR????→ChildP:ParentRChildP。

4）當且僅當父節點姿態屬性的變化無法引起子節點位置屬性的變化時，隔代影響將發生，即：

ParentR????→ChildP:ParentRDesendantP。

根據法則及串并聯形式，共提取10種動作基元，如表2所示。這些動作基元根據運動類型可以分為兩類：運動型和功能型。運動型動作基元描述的是末端位置發生變化的手臂自然運動；功能型動作基元描述的是末端位置不變的特殊運動，如避障、自運動等。主要關注的是運動型動作基元，文中的動作基元也泛指運動型動作基元。

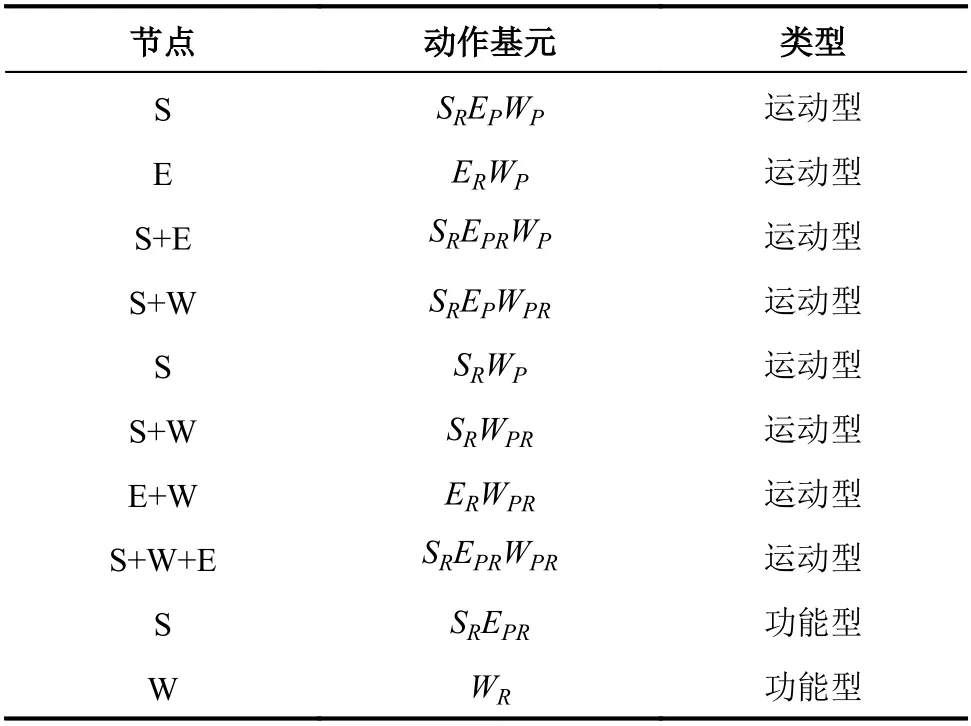
表2 動作基元Tab. 2 Movement primitives

表2中，節點指主動發生變化的各生理關節，即姿態屬性發生變化的關節。需要注意的是，根據擬人機械臂平臺的結構不同，各動作基元所包含的自由度也有所不同。建立動作基元的方法不僅適用于常見的7自由度擬人臂，對于具有生理關節（肩關節、肘關節、腕關節）配置的多自由度擬人臂同樣適用。

以動作基元SREPRWP為例，簡單介紹表2中動作基元的物理意義。節點S+E表示肩關節和肘關節的姿態屬性發生了主動變化，為驅動關節。其中，肩關節姿態屬性的變化引起了肘關節位置屬性的改變，而肘關節姿態屬性的變化又引起了腕關節位置屬性的改變。該動作基元描述的運動主要由肩關節和肘關節驅動完成，腕關節進行隨動。該運動類似于達點運動，即不考慮腕部姿態的變化。

2.3 動作基元間的連接形式

根據動作的定義，動作的初始和結束狀態都是靜止的，并且每個動作都具有明確的意義。因此，不同于動作元素的連接方式，動作基元之間只能進行串行連接。串行連接中最后一個動作基元往往是目標關鍵位姿，對動作的理解有時僅僅與最終的關鍵位姿有關。圖3為動作基元連接簡圖。圖3中：黑色圓圈表示不同的動作基元；從A到N代表基元執行順序；實心箭頭代表使能關系，即箭頭前段的基元為箭頭后端的基元做準備；空心箭頭表示修飾關系；每個基元都可以通過不同的語義函數E(x)進行修飾，從而豐富該基元的表現形式[17]；不同基元之間通過決策函數F(x)來進行選取和連接。根據不同動作基元的組合連接，可以構成豐富多樣的仿人運動，從而滿足不同任務的需求。

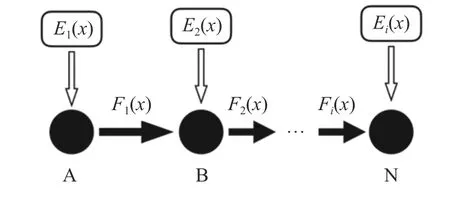
圖3 動作基元連接簡圖Fig. 3 Connection diagram of movement primitives

2.4 基于動作基元的運動框架

提出一種基于動作基元的擬人臂仿人運動框架，如圖4所示。該框架由4部分組成：智能決策層、子運動層、控制層及任務層。智能決策層是仿人運動規劃的基礎，動作基元是智能決策層的基礎。從智能決策層到任務層自左向右的過程是對具體任務進行規劃設計的過程，而從任務層到智能決策層自右向左的過程是對任務進行分解學習重構的過程。此外，通過接口與不同擬人臂的連接，該框架可實現不同擬人臂平臺的仿人運動任務，從而實現框架的通用性。

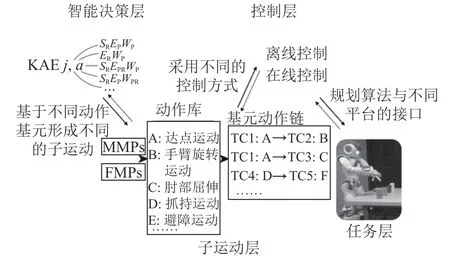
圖4 擬人臂仿人運動框架Fig. 4 Motion framework for anthropomorphic arms

3 綜合性逆運動學求解方法

根據動作基元的運動特點及NAO手臂結構，逆運動學問題可以通過兩種方法解決：基于幾何約束的反解算法和基于指標的反解算法。前者可通過特殊的幾何結構獲取解析解，對于不易獲得解析解的動作基元采用后者。本文重點介紹基于指標的反解算法。

3.1 基于指標的反解算法

對于其他動作基元，很難獲取解析解。本文利用梯度投影法（gradient projection method，GPM）解決該類基元的逆運動學問題[18]。GPM是一種基于廣義逆的算法，該算法將逆運動學問題的解分解為最小范數解和齊次解兩部分，具體的表達式如下：

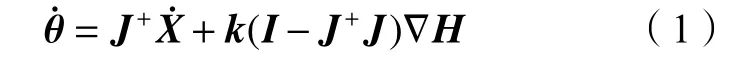
顯然，求解的關鍵在于目標函數H的確定。對于動作基元SREPWP、SREPRWP、SREPWPR、SRWPR、ERWPR、SREPRWPR，根據其腕部姿態在運動過程中是否改變又可以分為兩類，這兩類的目標函數H也有所不同。

3.1.1WP類動作基元逆運動學求解

動作基元SREPWP、SREPRWP所描述的運動類似于達點運動。在日常生活中，達點運動是最常見的運動，學者們對此進行了大量的研究。本文利用最小勢能指標[4]（minimum total potential energy，TPE）作為該類動作基元的臂姿預測指標。TPE由重力勢能（gravitational potential energy，GPE）和彈性勢能（elastic potential energy，EPE）兩部分組成，勢能f可定義如下：

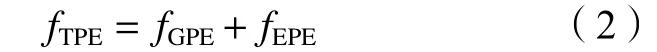
GPE可通過式（3）求解得到：

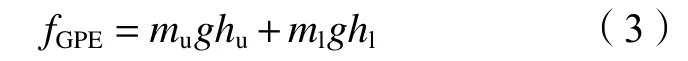
式中，mu、ml分別為大臂與小臂的質量，hu、hl分別為大臂與小臂質心的高度。

用一種變系數的虛擬扭簧模型計算EPE：

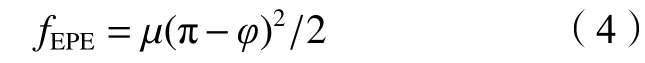
式中，φ為肘部旋轉角，μ為彈簧系數。

因此，WP類動作基元的目標函數為：

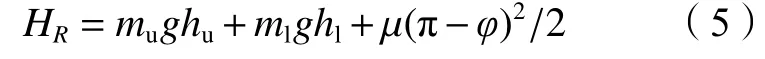
3.1.2WR類動作基元逆運動學求解

不同于動作基元SREPWP、SREPRWP，基元SREPWPR、SRWPR、ERWPR、SREPRWPR所代表的運動模型在運動過程中需要考慮腕部的變化。因此，在應用TPE的基礎上，需要考慮不舒適度所帶來的影響。具體表達如下：

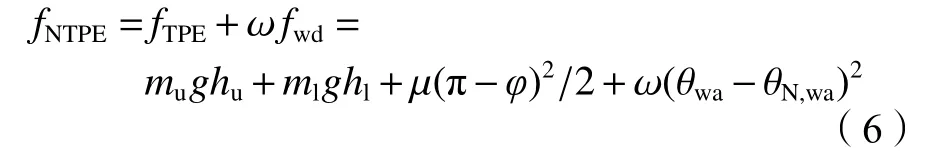
式中：ω為不舒適度指標的權重系數，fwd為腕部舒適度，并且可以通過多元回歸模型得到；θwa和θN,wa分別為腕部關節角和腕部中心角，中心角的選擇詳見文獻[19]。

同時，WR類基元所表達的運動形式與抓持運動相似。在生物物理學研究中，達點運動由大臂主導，而在抓取運動中，則是小臂起到主導作用。此時，小臂進行了大量的運動，而大臂受到小臂牽引靠著慣性進行隨動，其運動距離相對較短，這也意味著肘關節運動的距離較短。因此本文提出最小肘部位移指標以完善WR類基元的優化指標。最小肘部位移表示如下：

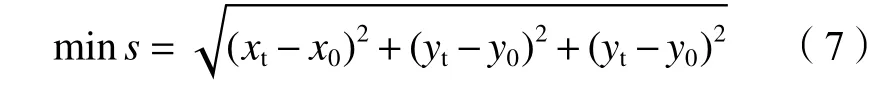
式中，(x0，y0，z0)表示肘關節中心點的初始位置，(xt，yt，zt)表示肘關節的目標位置。因此WR類動作基元的優化指標可表示為：

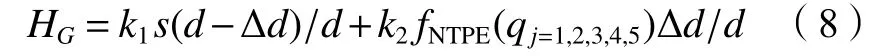
式中：k1和k2為權重系數；d為當WP類基元轉換為WR類基元時末端位置與目標位置的距離，當運動過程確定時，該距離為定值；?d為運動過程中末端位置與目標位置的實時距離，該距離為變量；(d–?d)/d和?d/d為過渡項。權重系數共同保證了不同動作基元之間的平穩過渡，防止運動過程中關節的突變。

3.2 基于幾何約束的反解算法

當NAO采用一些動作基元（如ERWP和SRWP）完成任務時，并不是所有關節都激活并參與到運動中。同時，運動過程中腕部的姿態并沒有發生改變。因此，當采用這類動作基元時，可以忽略腕部的運動。詳細的運動信息如表3所示。

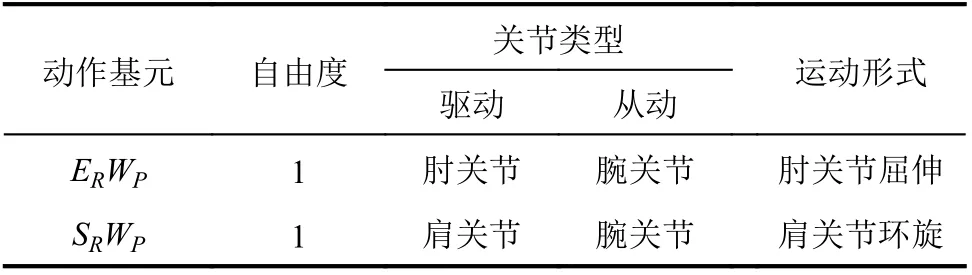
表3 ERWP和SRWP的運動形式Tab. 3 Motion information of the ERWP and SRWP

如圖5所示，本文引入了人臂三角形的概念描述手臂的構型，即由大臂和小臂組成的三角形[19]。在三角形中，可通過幾何關系快速準確地求得待求關節角，具體的推導過程不贅述。

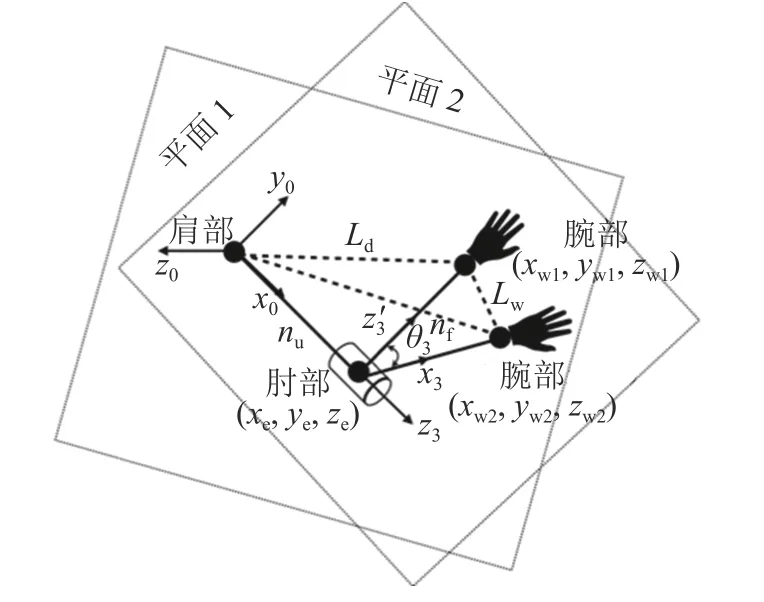
圖5 NAO平臺人臂三角形Fig. 5 Arm triangle of the NAO

4 實驗仿真

分別進行了相似性實驗和仿人運動實驗兩組實驗驗證。在相似性實驗中，通過對不同實驗者手臂運動的預測及對比，驗證所提方法的準確性，并對精度進行驗證。在仿人運動實驗中，通過在NAO平臺上進行的一組仿人運動實驗，驗證方法的可行性。

4.1 相似性實驗驗證

一共有20名實驗者參與到實驗之中，每名實驗者需要完成12組手臂運動實驗，每組實驗完成5次（20×12×5）。如圖6所示，這12個點在同一豎直面上按照3行4列的形式均勻分布，每兩點之間間隔為10 cm。實驗者按要求以手臂自然下垂作為初始位姿開始運動，運動數據通過運動捕捉系統（natural point inc.）獲取并作為比較數據。通過運動捕捉系統將采集到的人體運動數據將轉換為NAO配置下的運動數據，這樣既可以避免不同個體人臂臂長的差異性影響，也可以實現實驗結果數據的統一表達。等比例縮放方法用將實際人臂臂姿轉化為 NAO 的臂姿[7]。

圖6 相似性實驗Fig. 6 Similarity experiment

表4統計實驗者實驗過程中的運動信息，每一個實驗點需要20名實驗者共計完成100次實驗。表4時間為所有實驗者在完成該點實驗時所耗費的平均時間，實驗者初始手部位置和目標點位置之間的距離越長，平均時間越長；動作基元表示運動過程中基元發生的先后順序。從表4中可以看出，每名實驗者在達到同一點時采用的動作基元是相同的，但不同實驗點采用的動作基元卻不相同，這進一步說明了人臂運動具有相似性和多樣性的特點。在實驗過程中發現，當實驗者手臂初始位置與目標位置的距離較大時，往往采用較多的動作基元完成整個運動，同時動作基元發生的先后次序也較為固定。對于大多數的實驗點，實驗者往往采用基元SREPWP作為起始運動，驗證了達點運動是人臂日常運動中最為常見的運動形式。但是，當實驗者手臂初始姿態與實驗點目標姿態存在某種特殊關系（如點P11和P12）時，會采取其他動作基元作為起始運動，此時距離并不是決定基元發生的首要因素。

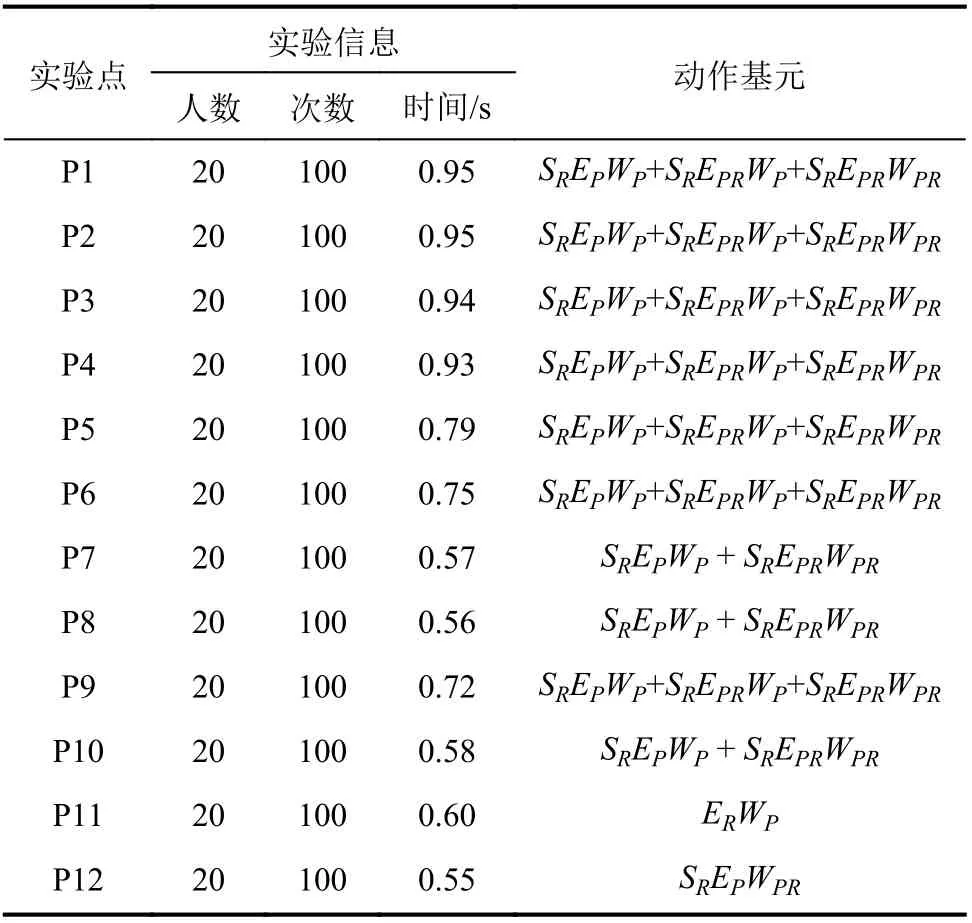
表4 相似性實驗運動數據Tab. 4 Motion information of the similarity experiment

在實驗過程中，通過運動捕捉系統及數據轉換算法將實驗者的末端軌跡及肘部位置可以轉換為滿足NAO手臂構型的運動數據。NAO采用同樣的動作基元模擬每一名實驗者在每一實驗點的運動過程，其關節角通過本文所提反解算法進行求解。最終，將NAO在運動過程中的肘部位置與實際實驗者的肘部位置進行比較，驗證本文所提方法的有效性。圖7為所有實驗者在不同點處的誤差分布。x、y軸分別表示列和行，其交叉點對應了12個實驗點；z軸為NAO肘部位置與實驗者實際肘部位置的距離誤差。圖7中每個交叉點附近的塊表示不同實驗者在該點處與NAO肘部位置的誤差。從圖7中可以看出，整體誤差在1 cm以下，能夠滿足仿人運動的精度要求。同時，當整個運動包含動作基元的種類較多時，誤差會越大。包含3種類型動作基元的實驗點的誤差（平均值0.767 1 cm，標準偏差0.113 2 cm）大于包含2種類型動作基元的實驗點誤差（平均值0.642 1 cm，標準偏差0.081 2 cm），而僅包含1種動作基元的實驗點的誤差是最小的（平均值0.21 cm，標準偏差0.123 1 cm）。造成這種情況的原因在于運動捕捉系統的誤差和實驗者運動時存在的不確定性，導致無法準確地預測出運動過程中從一種基元轉變為另一種基元時的精確位置；當運動過程中基元種類越多時，運動狀態轉換的次數也越多，相應的累積誤差也越大。實驗點P11處，反解算法采用的是基于幾何約束的反解方法，可以得到解析解，但是由于運動捕捉系統的系統誤差導致該點處仍然存在較小的誤差。

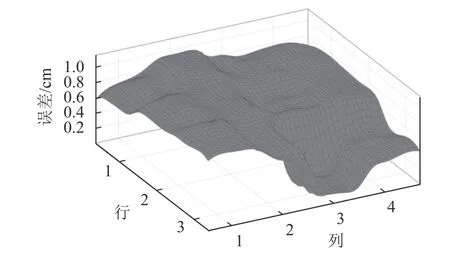
圖7 不同實驗點的肘部誤差分布Fig. 7 Elbow error distribution of all the points

圖8為每一名實驗者在所有點處的平均誤差及方差。圖8中，橫坐標表示20名實驗者，縱坐標表示不同實驗者的平均肘部誤差值。20名實驗者的標準偏差為0.022 7 cm，說明該方法能夠準確地模擬運動過程中不同實驗者的手臂姿態，從而保證了仿人運動的精度。

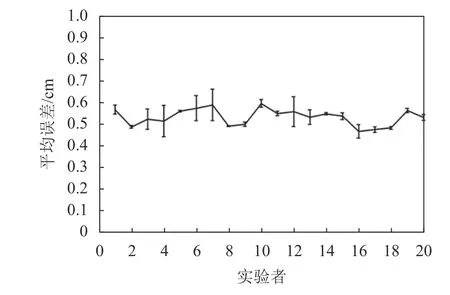
圖8 不同實驗者在所有實驗點處的肘部誤差分布Fig. 8 Elbow error distribution of all the subjects

4.2 仿人運動實驗驗證

利用本文所提方法在NAO機器人平臺上進行了一組仿人運動實驗，實驗內容為NAO機器人自主地產生類人化的打招呼動作。圖9為NAO機器人手臂運動過程。

圖9 仿人運動實驗過程Fig. 9 Process of human-like movement experiment

實驗開始前，10名實驗者完成相同的運動，其手臂運動數據通過運動捕捉系統進行采集。運動過程中的部分手臂關鍵臂姿作為NAO機器人的目標臂姿。運動捕捉系統將采集到的運動數據同樣進行標準化處理并轉換為符合NAO手臂構型的運動數據。

將采用本文算法得到的臂姿與分別采用最小勢能法和最小二乘法產生的臂姿進行了比較。相似性指標用于計算預測臂姿與實際臂姿的相似度，其表達式如下：

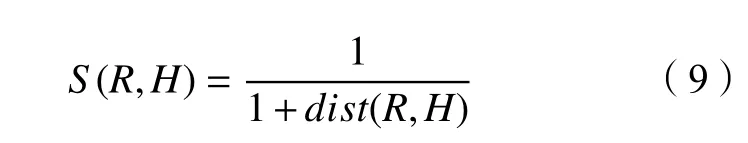
式中：R、H分別表示預測得到的機械臂臂姿和實際人臂臂姿；S(R，H)表示相似度，其值域在(0，1]之間，數值越大，兩者相似度越高；dist(R，H)表示機械臂臂姿及人臂臂姿在N維空間中的距離，對于NAO機器人，其手臂關節具有5個自由度，因此N為5。dist(R，H)可由式（10）計算得到：

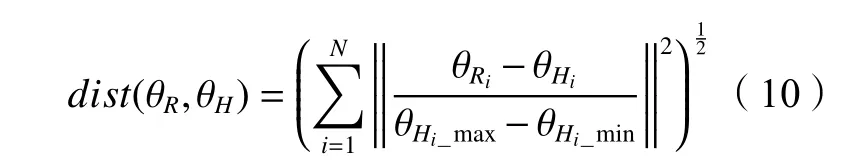
式中，θRi和θHi分別表示機械臂和手臂的第i個關節角，[θRi_min， θRi_max]表示第i個關節角的范圍。

3種不同算法的相似度值如圖10所示，橫坐標表示運動幀數，縱坐標表示相似度值。圖10中，曲線的數值越大，預測的臂姿越接近真實臂姿。

由圖10可知：與最小二乘法相比，本文所提的動作基元法及最小勢能法在仿人運動規劃上有明顯的優勢。同時，動作基元法和最小勢能法由于在某些階段（幀數為60～80），采用的運動模型較為相似，則在這些階段兩種方法的相似度值較為接近。但是在整個運動過程中，最小勢能法所得的相似度值（平均值0.913 1，標準偏差0.009 1）要小于動作基元法的相似度值（平均值0.961 1，標準偏差0.009 4）。這是因為最小勢能法將運動中的手臂模型視為單一模型，在運動過程中并不會發生改變，忽視了人臂運動多樣性的特點，因此無法保證全局的準確性。通過上述對比，說明本文所提方法在處理仿人運動多模型的問題上具有很好的優勢，能夠滿足仿人運動的要求。

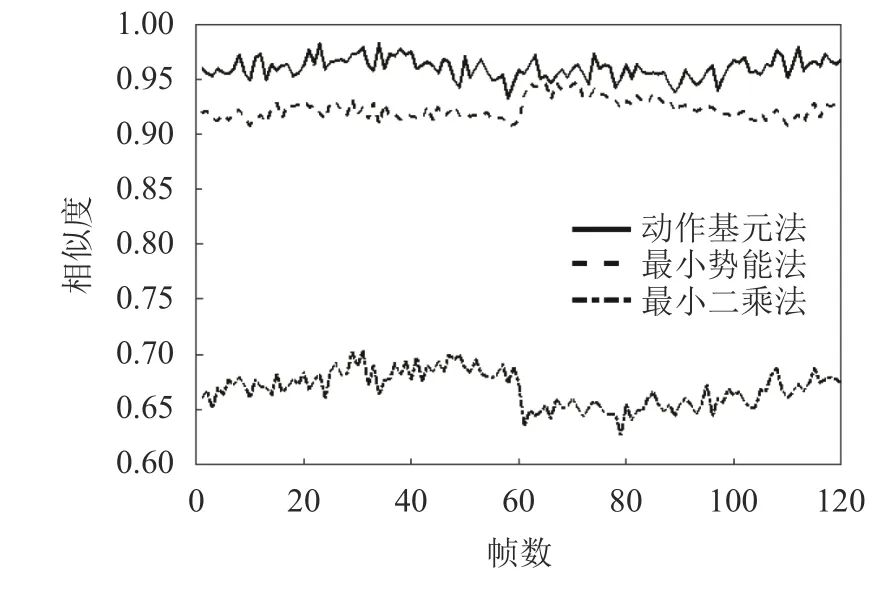
圖10 3種算法的相似度曲線Fig. 10 Similarity curves of three algorithms

5 結 論

提出了一種基于動作基元的規劃方法實現擬人機械臂的仿人運動。基于動作基元的人臂運動表達方法不僅具有清晰的物理意義，能夠反映出人臂運動的內在規律，而且模塊化的建模思想將復雜的運動集合離散為多個、簡單的運動子集。既能夠保證較高的仿人運動精度，也為擬人臂仿人運動規劃算法提供了便利。同時，該表達方法并不依賴于自由度數，只要目標平臺具有明確的生理關節即可適用。最后，分別建立不同模型下的臂姿預測指標，并在NAO機器人平臺上驗證了方法的有效性。

基于動作基元的人臂運動表達是一種泛化的表達人臂運動的方式。通過對人臂生理關節的屬性分析，確立了人臂運動的種類。但是在這些類別中，根據擬人臂機械關節的不同運動方式及環境約束，同一基元依然有不同的運動方式。動作基元的提出實際上是實現手臂模型的解耦，在下一階段的研究中，將重點實現運動過程的解耦，從手臂模型和運動過程兩方面共同完成手臂運動的解耦，從而進一步提高擬人臂仿人運動的精度。