基于運動學的機器人腳輪數學模型構建與仿真

周燁

（常州劉國鈞高等職業技術學校，江蘇 常州 213000）

1 概述

數學及數學工具如MATLAB 現已滲透到各個工程領域并開展了廣泛深入的應用，正是這些應用的廣泛和深入推廣，推動了工程領域的高速發展。在工程領域，全向移動機器人具有平面內三個自由度（即具有全向移動性），適合在狹小的工作空間內移動[1]。經查閱文獻，國內對主動腳輪研究甚少，僅在文獻[2]中進行了研究，其研究方向側重于控制算法研究[2]。同時，文獻[3]表明主動腳輪是全向移動機器人的理想行走機構。因此，本文對機器人腳輪展開研究，利用腳輪基本的幾何和運動關系，構建并推導了腳輪速度的數學關系表達式及運動學數學模型，同時進一步采用數學仿真工具MATLAB 對其進行仿真計算，獲得了該腳輪的運動學解，驗證了本文所構建的數學模型的正確性，為機器人腳輪及相近領域提供一定的分析參考。

2 移動機器人的運動學分析

2.1 移動機器人的結構簡述

機器人主動腳輪具有驅動能力，主動腳輪具有驅動電機和轉向電機兩個電機同時驅動。其結構有驅動電機、齒輪、皮帶等。

2.2 機器人腳輪滑動的數學關系表達

2.3 腳輪運動學模型建立

根據兩腳輪的幾何關系，同時對角度以時間進行求導，得出兩輪子作用到移動機器人幾何中心的速度為：

整理成矩陣形式腳輪1 的運動學模型為：

3 仿真求解與軌跡規劃

3.1 軟件仿真求解結果

采用數學工具MATLAB 軟件對上述模型進行求解，將模型的尺寸參數、電機轉速參數作為輸入條件，其中結構參數為：m=692.82mm，r=b=50mm。在軟件中獲取機器人進行原地轉向1s后，得到機器人的各運動關節數據如圖2 所示。

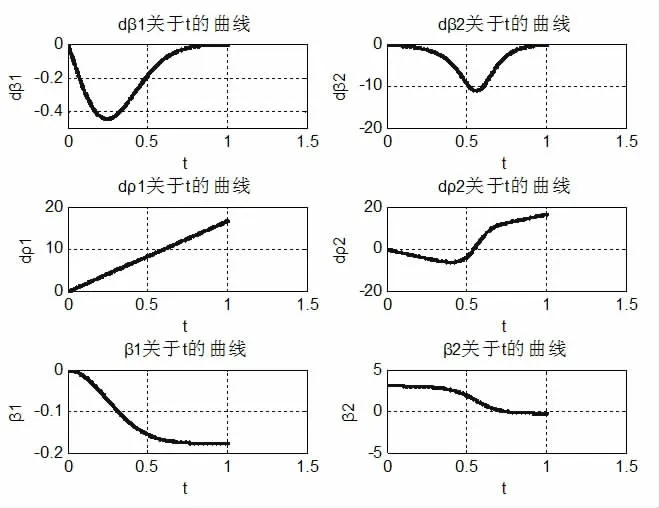
圖2 腳輪軟件求解結果曲線

3.2 移動機器人腳輪軌跡規劃

軌跡規劃是移動機器人進行運動控制的關鍵步驟，是分析計算的目的和意義所在。軌跡規劃發方法很多，目前普遍的是多項式法。由于采用五次多項式進行插值能保證位置、速度、加速度以及加價速度的曲線平滑，因此本文采用五次多項式法進行軌跡規劃。在XY 平面用五次樣條曲線對移動機器人進行軌跡規劃后得到的位置（P），速度（V），加速度（a）曲線值如圖3 所示。

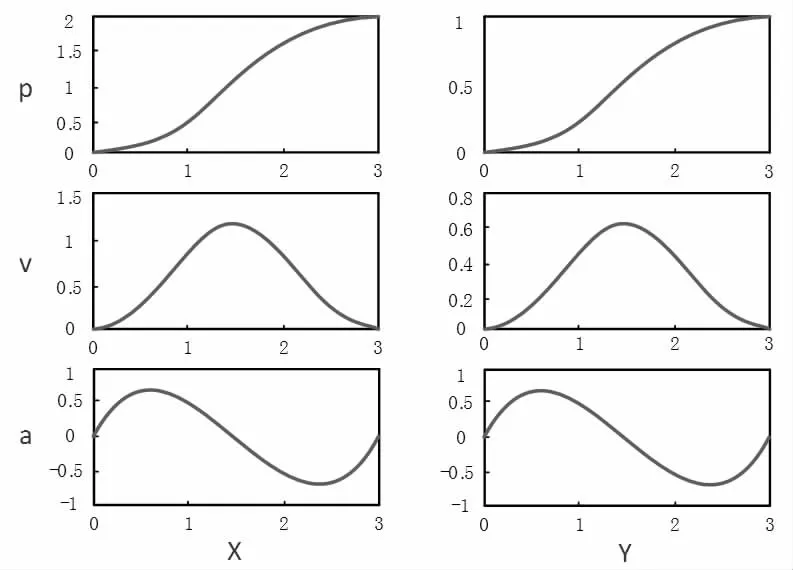
圖3 機器人的位置、速度、加速度曲線圖

從仿真結果來看：對于移動機器人進行速度規劃，令移動機器人的運動軌跡為一個矩形；移動機器人以0.25m/s2的加速度加速2s 后，以0.5m/s 的速度勻速行駛4s，最終以0.25m/s2的加速度減速到靜止；移動機器人以-0.25m/s2的加速度加速2s 后，以0.5m/s 的速度實現倒行，最終以0.25m/s2的加速度減速到停止；移動機器人以0.25m/s2的加速度加速2s 后，實現以0.5m/s的速度勻速側向移動4s，最終以0.25m/s2的加速度減速到靜止。移動機器人的運動仿真與預期規劃好的運動軌跡完全吻合，文中所建立的移動機器人的運動學模型合理。

4 結論

采用數學及其數學工具，針對一種機器人腳輪展開分析，利用腳輪基本的幾何和運動關系構建并推導了腳輪速度的數學關系表達式及運動學數學模型，進一步對其仿真求解驗證了模型的正確性；并在此基礎上進一步采用五次多項式進行了軌跡規劃，獲得了較好的控制目標，能夠為機器人腳輪的設計計算提供一定參考和借鑒。