CeAuGa3的力學性質及磁性的第一性原理計算

程耀世， 劉本瓊

(中國工程物理研究院核物理與化學研究所， 綿陽 621999)

1 Introduction

It is very attractive to study the Cerium-based intermetallic compounds, since they exhibit lots of interesting behaviors resulting from the interplay between the single-impurity Kondo effect and the Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions. Especially, the stoichiometric compounds with the general formula CeTX3or CeTyX4-y(Tis a transition metal,Xis a simple metal) have recently received great attention, because important new features have been observed in addition to their novel ground state properties which have been studied extensively. For examples, there is relatively low Cu-Al atomic site disorder[1-2]in CeCuAl3, which leads to the previous argument about its true crystal structure of either the ThCr2Si2-type[3]or the BaNiSn3-type[4-5], and indeed can influence the electronic properties. CeNiGe3undergoes antiferromagnetic (AFM) phase transition belowTN= 5.5 K at ambient pressure and exhibits a quantum critical point at about 6～7 GPa. The superconductivity in this material exists in a wide range of 1.7～9.3 GPa[6-7], and the spin-fluctuations may be not the hidden mechanism at the lower pressure region. Kimuraetal.[8]presented an unconventional pressure-induced superconductor CeRhSi3, where the superconductivity and the AFM state coexist, withTN=1.6 K at ambient pressure. Another similar example is the antiferromagnet CeIrSi3, where superconductivity appears in 1.8～3.5 GPa[9]. Although most of CeTX3compounds show AFM ordering at low temperature, CeAgAl3[10]is a scarce example of ferromagnetic compound withTC= 3.0 K. Further, selected members of this class offer the new insights that magnetoelastic coupling could result in the formation of a bound state between low-lying phonons and a crystal electric field (CEF) excitation. Adrojaetal. first reported the presence of an additional magnetic excitation in the neutron spectra of CeCuAl3measured in the paramagnetic phase[11], which cannot be explained by a pure CEF model. By generalizing the theoretical model proposed by Thalmeier and Fulde for the cubic system CeAl2[12-13]to the tetragonal point-group symmetry, a satisfactory interpretation for the magnetic inelastic neutron scattering spectra of CeCuAl3can be achieved. In recent studies of CeAuAl3[14-15], except for the pronounced vibronic bound state, a well-resolved anti-crossing of the CEF excitations with the acoustic phonon branch at zero magnetic field has also been observed by neutron scattering.

In this work, we present detailed first-principles calculations of the structural and mechanical properties of CeAuGa3, which has been rarely studied and may behave qualitatively similarly to CeAuAl3. Total energies of different spin arrangements of CeAuGa3have been compared, and our results show that the total energy of ferromagnetic (FM) configuration is indeed the lowest,i.e., in the ground state a FM ordering state is favored. By further analyzing the paths of spin exchange coupling, it is found that all the spin exchange interactions are positive ferromagnetic type. The couplings between the Ce ions parallel to theabplane are comparable, while the third-nearest-neighbour coupling between the Ce ions within adjacent layers is relatively weak.

2 Computational methods

Several different spin configurations of CeAuGa3were examined by evaluating the exchange coupling constants between the Ce ions via mapping analysis based on first principles calculations. The Viennaabinitiosimulation package (VASP)[16-18]was used, with the standard frozen-core projector augmented wave (PAW) method, and the generalized gradient approximations (GGA) for the exchange and correlation corrections. The plane-wave cutoff energy was tested and set to 550 eV. According to the Monkhorst-Pack scheme, thek-point meshes in the Brillouin zone were sampled by 10×10×5 grids. For the elastic property calculations, a denserk-mesh sampling of 12×12×6 was adopted for accuracy. In order to obtain the phonon dispersion, Phonopy code[19]was used and a 2×2×2 supercell was constructed with thek-point meshes of 4×4×4. Other parameters included a convergence criterion of the Hellmann-Feynman force of 0.01 eV/?, and 10-8eV for the total energy tolerance.

3 Discussion

3.1 Spin exchange parameters

According to Mocketal.[20], CeAuGa3crystallizes in the non-centrosymmetric BaNiSn3-type tetragonal structure (space group is I4mm, No.107). There are 10 atoms in the conventional unit cell, as shown in Fig. 1. The lattice parameters area= 4.337 ?,c= 10.66 ?, giving ac/aratio of 2.458. When doing geometry optimization, we start with the experimental geometries and calculate the dependence of the total energyEon the volumeV. For the tetragonal structure, we first calculate total energies for different volumes by fixing thec/aratio and changing the lattice parametera, and do a least-squares fit of theE-Vcurve to the third-order Birch-Murnaghan equation of state (EOS)[21],

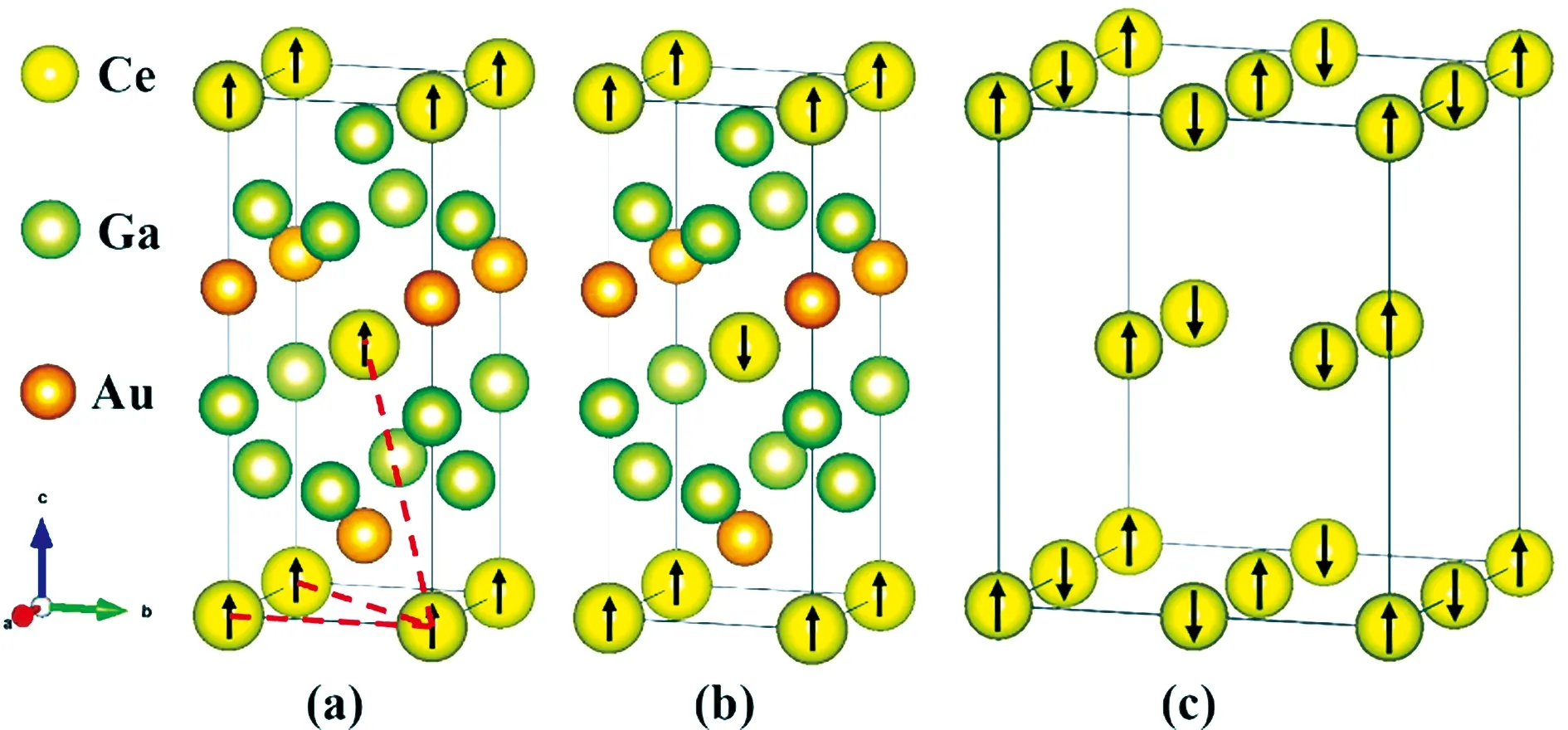
Fig.1 Ordered spin arrangements of Ce ions in the (a) FM, (b) AFM1 and (c) AFM2 states of CeAuGa3 (color online)The red dashed lines in (a) refer to the three spin exchange paths J1, J2 and J3 of Ce ions, respectively. For the ordered spin arrangement in AFM2 (c), only magnetic Ce sites are displayed for clarity in the 2 × 2 × 1 supercell

(1)

withE0being the equilibrium energy,V0the equilibrium volume, andB0′ the pressure derivative of the bulk modulusB0. Secondly, we fix the value of lattice parametera= 4.368 ? at the energy minimum, and change the volume by adjusting thec/aratio, as shown in Fig. 2. After the second EOS fit, the lattice parameters of CeAuGa3are finally determined asa= 4.384 ?,c= 10.655 ?,c/a= 2.43, and the equilibrium volumeV0= 204.75 ?3, which are in good agreement with the experimental data[20], as listed in Tab. 1. Among the different spin configurations of CeAuGa3(i.e., non-magnetic state NM, ferromagnetic state FM, and two different AFM states), the FM structure has the lowest total energy, indicating that the ground state prefers to be ferromagnetic ordering.

Tab.1 Calculated lattice parameters (a,c), the c/a ratio, the equilibrium volume (V0) and relative energies (E0) of CeAuGa3, compared with previous experimental results

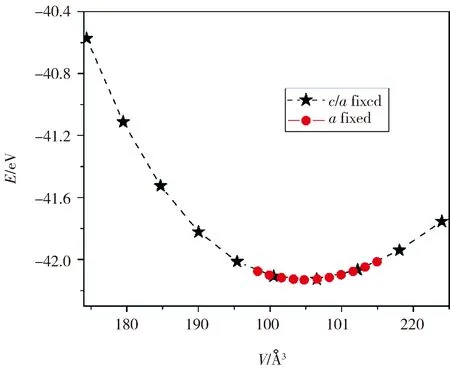
Fig.2 The relationship between the total energy E and the unit cell volume V of CeAuGa3 (color online)

The lines represent a least-squares fit to the third-order Birch-Murnaghan equation of state. The black stars denote that the data are obtained by fixingc/a= 2.458, and the red cycles correspond to the case of fixeda= 4.368 ?

Based on the total energy calculations, one may analyze the magnetic state in terms of three spin-exchange parameters,i.e., the exchange couplingJ1between the nearest-neighbour Ce ions along thea(b) direction, the exchange couplingJ2between the next-nearest-neighbour Ce ions along the diagonal path within theab-plane, and the exchange couplingJ3between the third-nearest-neighbour Ce ions between the adjacent //ablayers, as denoted in Fig.1(a). To extract the values of the spin-exchange parameters, we express the total spin exchange interaction energies of the three ordered spin states in terms of the effective Heisenberg Hamiltonian,

(2)

whereJijdenotes the spin exchange parameter (fromJ1toJ3) for the spin exchange interaction between the spin sitesiandj,SiandSjare the spin angular momentum operators. By applying the energy expressions obtained for spin dimers[22-24], the total spin exchange energies of the three ordered spin states can be obtained as

EFM=E0-50J1-25J2-50J3

(3)

EAFM1=E0-50J1-25J2+50J3

(4)

EAFM2=E0-175J1-62.5J2-200J3

(5)

By mapping the relative energies of the three-ordered spin states determined by first-principles calculations onto the corresponding relative energies determined from the above spin-exchange energies, one can obtainJ1= 0.572 meV,J2= 0.414 meV andJ3= 0.043 meV listed in Tab. 2. All the spin exchange parametersJ1,J2,J3are positive, indicating ferromagnetic interactions between the Ce ions, and further supporting the ferromagnetic ground state of CeAuGa3. The exchange coupling between the nearest-neighbour pairsJ1and that of the next-nearest-neighbour pairsJ2dominate, while the third-nearest-neighbour exchange couplingJ3may be negligible.

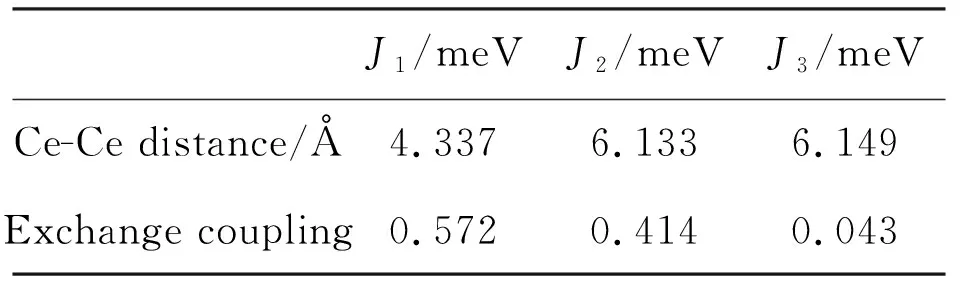
ab.2 Ce-Ce distances associated with the spin exchange paths J1～J3 of CeAuGa3, and the values of J1～J3 determined by mapping analysis based on the present first-principles calculations

3.2 Elastic properties

For tetragonal structures, there are six independent elastic constants,i.e.,C11=C22,C12,C13=C23,C33,C44=C55, andC66. Under small deformations, the total energyEof a crystal associated with a strainecan be expressed as follows:

(6)

whereeiandejare components of the straine= (e1,e2,e3,e4,e5,e6). According to Eq. (6), all the elastic constantsCijcan be deduced by fitting the strain energy for particular deformations. We employ six different strain states for elastic constants calculations as listed in Tab. 3. For each strain type, 14 symmetric values of strains fromδ=-0.0175 to 0.0175 are taken to make the strain energy fit with a step of 0.0025. The corresponding energy-strain data is shown in Fig.3, and the calculated elastic constants are summarized in Tab. 4.

Tab.3 Strain states used to determine the elastic constants of CeAuGa3

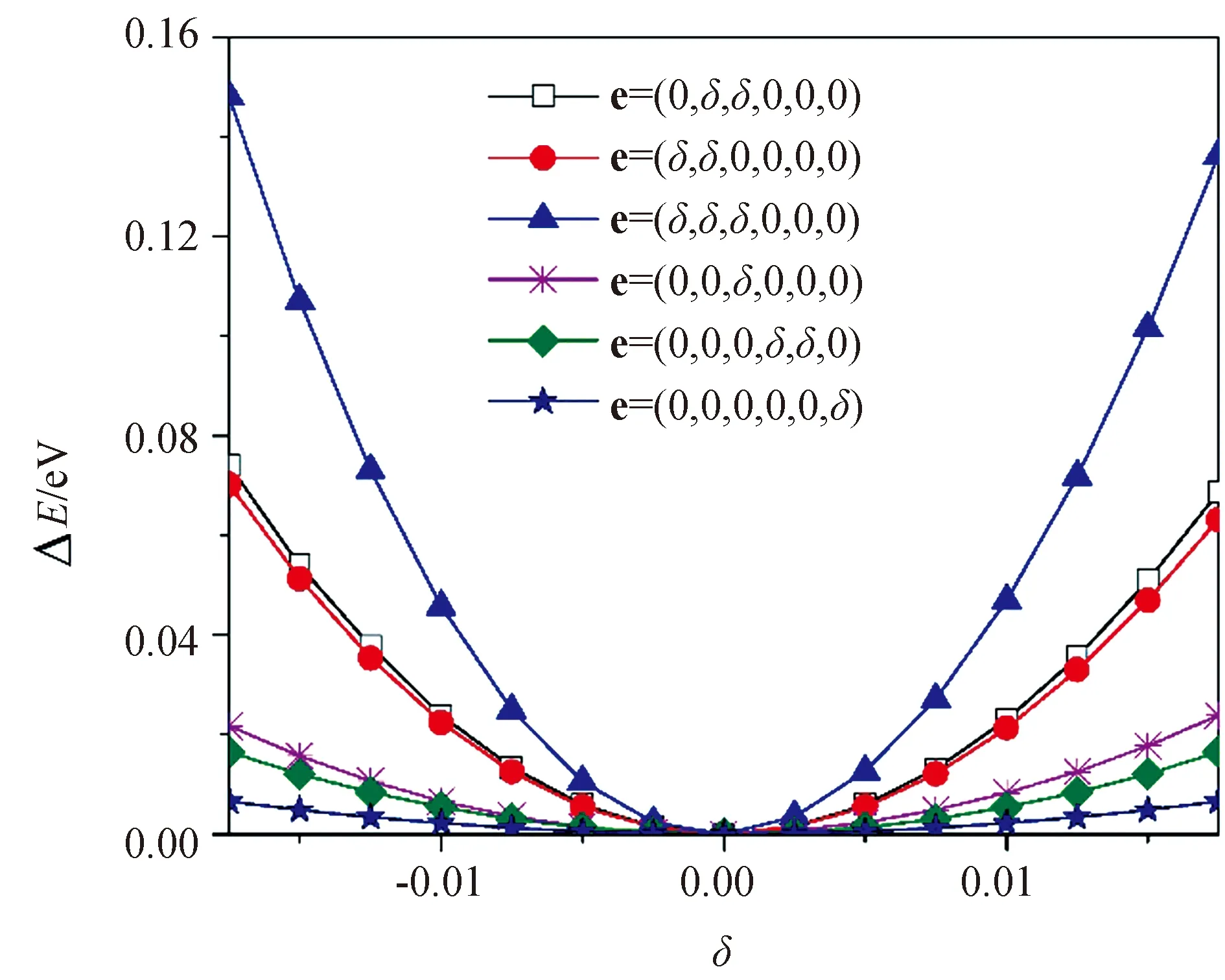
Fig.3 Energy-strain data for CeAuGa3, lines connecting data points are shown to guide the eye only(color online)

Tab.4 The calculated elastic constants Cij, bulk modulus B, shear modulus G, Young’s modulus Y and Poisson’s ratio ν of CeAuGa3

One can find that all the predicted elastic constants fulfill the well-known Born-Huang stability criteria[25],

C11-C12>0

(7)

C11+C33-2C13>0

(8)

C11>0,C33>0,C44>0,C66>0

(9)

2C11+C33+2C12+4C13>0

(10)

which confirms that CeAuGa3is mechanically stable. We have also checked the dynamical stability by the full phonon dispersion relation calculations[26]using the small displacement method[27], as shown in Fig. 4. There are in total 15 phonon branches, and all the calculated phonon frequencies along the high-symmetry directions Г-X-R-S0-Г and Г-M-S-N-P-G-M in the Brillouin zone are positive, suggesting a dynamically stable structure.

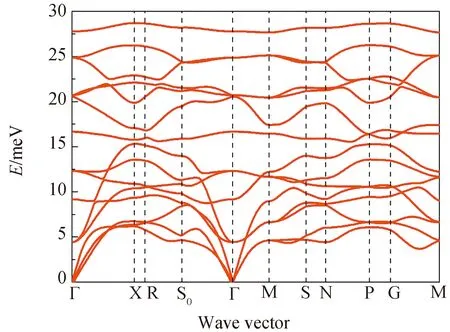
Fig.4 Phonon dispersion curves of CeAuGa3 along high symmetric directions

Based on the obtained six single-crystal elastic constants of CeAuGa3, one can further obtain its polycrystalline average isotropic bulk modulusBand shear modulusGaccording to the Voigt-Reuss-Hill approximation[28-30]:

(11)

(12)

(13)

(14)

6/(C11-C12)+6/C44+3/C66]

(15)

The Young’s modulusYand Poisson’s ratioνcan be obtained as

(16)

The calculated bulk modulus, the shear modulus, Young’s modulus and Poisson’s ratio for CeAuGa3are also summarized in Tab. 4. For polycrystalline phases, a high (low) ratio of bulk to shear modulusB/Gis associated with ductility (brittleness) of the material[31]. The value of CeAuGa3is as high as 6.37, suggesting a high ductility of this compound.

4 Conclusions

Based on first-principles calculations, we have studied the structural properties for several different magnetic states of CeAuGa3. The total energy comparison shows that its ground state prefers to be ferromagnetic ordering. By mapping analysis of different spin states, one can find that all the exchanges between Ce ions are positive (ferromagnetic type). The exchange coupling between the nearest-neighbour pairs and that of the next-nearest-neighbour pairs of Ce ions dominate, while the third-nearest-neighbour interaction between the Ce spins within adjacent //ablayers is relatively weak. In additions, we have checked the mechanical and dynamical stabilities by computing the elastic properties and phonon dispersion, respectively. Our results imply that CeAuGa3is both mechanically and dynamically stable, since all the calculated elastic constants satisfy the well-known Born-Huang stability criteria, and without any imaginary phonon modes for all the wave vectors in the Brillouin zone.