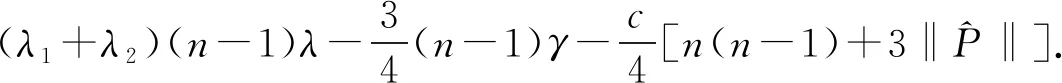局部共形Kaehler空間子流形的陳不等式
2021-10-18 00:48:38吳彤
東北師大學(xué)報(自然科學(xué)版) 2021年3期
吳 彤
(東北師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,吉林 長春 130024)
1 預(yù)備知識
Chen建立了陳不等式后,許多幾何學(xué)者對不同空間不同聯(lián)絡(luò)的陳不等式進(jìn)行了研究[1-4].文獻(xiàn)[5]研究了實空間半對稱度量及非度量聯(lián)絡(luò)的陳不等式.


(1)
其中P是N上的向量場,并且π(Y)=ɡ(P,Y).


(2)
其中:





(3)
數(shù)量曲率τ在x點為
(4)
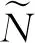
2 主要結(jié)論及證明

(5)


(6)
設(shè)Π=span{e1,e2},并且令
tr(α|Π)=α(e1,e1)+α(e2,e2),
tr(h|Π)=h(e1,e1)+h(e2,e2),
則有

(7)
同理有

(8)
那么

(9)
所以
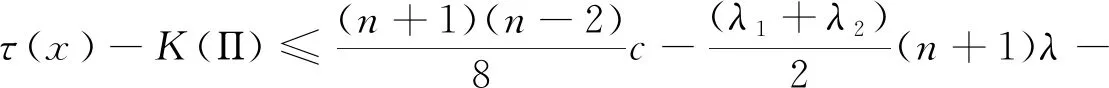
(10)
通過文獻(xiàn)[7]引理2.4,可知
(11)
則定理成立.

(12)

(13)
(14)

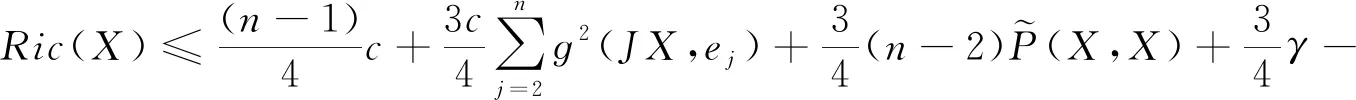
(15)
證明設(shè)X∈TxM是在x點的單位切向量,選擇一組標(biāo)準(zhǔn)正交基{e1,…,en},令e1=X.則

(16)


(17)
證明在x點選擇一組標(biāo)準(zhǔn)正交基{e1,…,en,en+1,…,en+p}使得en+1平行平均曲率向量H(x),則