不確定整數階分數階單擺混沌系統的自適應滑模同步
孟 曉 玲
(鄭州航空工業管理學院數學學院,河南 鄭州 450015)
1 預備知識
分數階系統同步取得了很多研究成果.[1-9]文獻[10]對一類不確定分數階混沌系統實現了積分滑模同步;文獻[11]實現了分數系統主動滑模同步;文獻[12]實現了同步時間的估計;文獻[13]實現了分數階不確定Victor-Carmen混沌系統的滑模同步.另一方面,單擺混沌系統引起了眾多學者的高度關注.文獻[14]研究了整數階分數階單擺混沌系統的混沌同步;文獻[15]研究了分數階單擺混沌系統的終端滑模同步.系統的不確定性是影響系統不穩定的根源,另外利用自適應方法研究不確定分數階單擺混沌系統方面的結果還是比較少的.本文研究不確定整數階和不確定分數階單擺系統的自適應滑模混沌同步,給出了不確定整數階及不確定分數階單擺混沌系統的自適應滑模同步,通過設計適應律和控制器得到單擺系統獲得滑模同步的2個相關結論.
定義1[16-17]分數階Caputo微分可定義為

2 主要結果
分數階單擺系統可以描述為
(1)

(2)
其中:y(t)=(y1,y2)T,[0,+∞)和di(t)為不確定項和外擾,ui(t)代表控制量.
假設1 不確定項Δfi(y)和外擾di(t)均有界,即存在未知常量mi,ni>0,滿足
|Δfi(y)| 定義ei=yi-xi(i=1,2),則有 (3) 引理1[18]若x(t)為連續可微的函數,則對任意的t≥0,有 自適應控制律為 從而ei(t)→0,滑模面穩定. 整數階單擺混沌系統描述如下: (4) 設計(4)為主系統,從系統如下: (5) 定義ei=yi-xi(i=1,2,…,n),從而得 (6) 自適應律設計為 兩邊積分得 由引理3,得si→0?ei(t)→0,則系統(4)與(5)是滑模同步的. 分數階單擺混沌系統的系統誤差如圖1—2所示. 圖1 第1誤差變量 圖1 第2誤差變量 本文研究了單擺混沌系統的滑模同步,給出了帶有不確定性和有界擾動的單擺混沌系統獲得滑模同步的結論,設計出新型趨近速度更快的滑模函數是下一步考慮的嶄新課題.











3 數值仿真
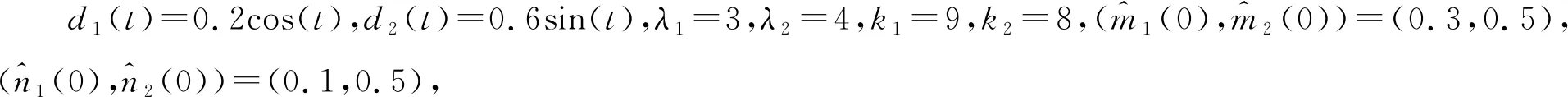


4 結論

