緊抓主線?提升能力?發展素養
鄢堅

摘 要:在中考“統計與概率”的章節復習中,若能策略得當,課堂教學安排有序,以教學內容為載體,重在梳理整合知識,感悟數學思想和方法,定能提升學生關鍵能力,發展數學素養。
關鍵詞:緊抓主線;提升能力;發展素養;“統計與概率”的章節復習策略
《義務教育數學課程標準(2011年版)》指出:在數學課程中,應當注重發展學生的數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力、模型思想。為了適應時代發展對人才培養的需要,數學課程還要特別注重發展學生的應用意識和創新意識。其中數據分析觀念主要表現在:能從統計的角度思考與數據信息有關的問題;能通過收集數據、整理數據、描述數據、分析數據的過程做出合理的決策,認識到統計對決策的作用;能對數據的來源、處理數據的方法,以及由此得到的結果進行合理的質疑。而在《普通高中數學課程標準(2017年版)》中的數學學科六大核心素養中則提到數據分析主要表現在:收集和整理數據、理解和處理數據、獲得和解釋結論、概括和形成知識。通過高中數學課程的學習,學生能提升獲得有價值信息并進行定量分析的意識和能力,適應數字化學習的需要,增強基于數據表達現實問題的意識,形成通過數據認識事物的思維品質,積累依托數據探索事物本質、關聯和規律的活動經驗。由此可以看出,初高階段對“數據分析”的要求是逐步提升的,因此在中考《統計與概率》的章節復習中,“復習策略是否得當,關鍵能力能否提升,數學素養如何發展?”需引起教師足夠重視。以下談談中考“統計與概率”的章節復習策略。
一、 緊抓一條主線——統計思想、隨機觀念
統計主要研究現實生活中的數據,數據分析是統計的核心。通過對數據的收集、整理、描述、分析,來幫助人們解決問題,依據數據思考和處理問題,通過數據發現事物發展規律是統計的基本思想;從總體中抽出樣本,通過分析樣本數據來估計和推測總體的情況,用樣本估計總體也是統計的基本思想,這些思想貫穿第三學段“統計和概率”的相關章節。在個別實驗中呈現不確定性,而在大量重復實驗中,又具有某種統計規律的現象,就是研究隨機現象時要討論的問題。而這種隨機觀念的培養是在統計中通過抽樣來體會總體及估計結果的隨機性的過程中實現的。抓住了統計思想、隨機觀念這一主線,也就抓住了“統計和概率”知識與方法的源頭。
二、 發展兩大素養——數據分析和數學運算
統計觀念是指由一組數據所引發的想法,能推測到的可能結果以及自覺地想到用統計的方法解決問題,必須經歷統計活動的過程才能培養出來的一種感覺。如在收集、整理、描述和分析數據的統計活動中,將概念、方法與原理統一到數據處理活動中去,逐步學會用數據說話,并對結論進行解釋或思辨,感受統計結果對決策的意義和作用,從而建立并發展數據分析觀念。而數據處理過程必然伴隨數學運算,合理利用數據、有效借助運算解決實際問題,通過運算促進數學關鍵能力的提升及數學素養的發展。
三、 關注三個細節
(一)關注統計量相關概念的復習與辨析
通過對統計量相關概念的復習與辨析,強調對其統計意義的理解,如“平均數、中位數、眾數、方差”“頻數、頻率、概率”等,通過實例創設分析、選擇恰當統計量解決問題的情景,進行比較、總結、歸納統計量各自的特點,反映數據哪方面的特征,如何利用它們獲取更多的信息等。
(二)關注熱點問題中統計思想的滲透
通過對近幾年各地中考試卷中的“統計和概率”試題收集分類,如對四大熱點:(1)統計圖表信息的提取——關注數據的收集;(2)統計量的計算——關注統計量的選擇;(3)概率及其應用——關注頻率與概率;(4)統計觀念——關注統計圖的完整畫法。對上述四大熱點進行專題強化訓練,以提高學生答題能力。在這過程中,教師有意識地滲透統計思想方法——統計知識與方法的源頭,進而提升關鍵能力,發展數學素養。
1. 統計圖表信息的提取——關注數據的收集
數學中的統計圖表,擁有直觀性和兼容性兩大優勢,常被作為載體來考查學生對于數據的觀察、分析、計算、判斷等能力,是應用數形結合思想解決數學問題的重要內容之一,其關鍵是理解平均數、眾數、中位數、頻率、頻數、方差等基本概念,同時要求學生具有一定的“讀圖能力”,意識到圖形會說話,通過對統計圖表的分析和歸納,搜索出我們需要的數據信息,進而通過計算歸納求解,發展關鍵能力。
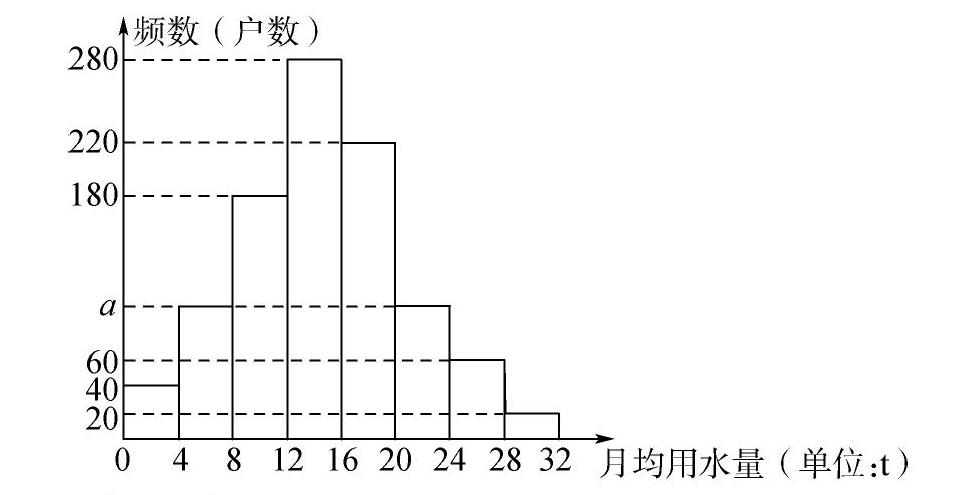
【例1】 (2020福州二檢)某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費。
方案:一戶家庭的月均用水量不超過m(單位:t)的部分按平價收費,超出m的部分按議價收費。為此擬召開聽證會,以確定一個合理的月均用水量標準m。通過抽樣,獲得了前一年1000戶家庭每戶的月均用水量(單位:t),將這1000個數據按照0≤x<4,4≤x<8,…,28≤x<32分成8組,制成了如圖所示的頻數分布直方圖。
(1)寫出a的值,并估計這1000戶家庭月均用水量的平均數;(同一組中的數據以這組數據所在范圍的組中值作代表)
(2)假定該市政府希望70%的家庭的月均用水量不超過標準m,請判斷若以(1)中所求得的平均數作為標準m是否合理?并說明理由。
解:(略)
評注:本題考查了加權平均數、用樣本估計總體,統計結果對決策的意義和作用等知識,解題的關鍵是牢記概念及公式。
2. 統計量的計算——關注統計量的選擇
遇見涉及“統計與概率”相關知識的數學問題,學生需認真讀題、讀懂圖表中的提供的信息,關注統計量的選擇。如反映數據集中程度的平均數、中位數、眾數各有局限性,只有對平均數、中位數、眾數、方差等統計量的理解到位,才有能力對統計量進行合理的選擇和恰當的運用:1. 平均數極好地反映數據集中趨勢,其兩個運算公式x=x1+x2+x3+…+xnn,x=x1f1+x2f2+x3f3+…+xnfnf1+f2+f3+…+fn是中考高頻考察公式,應用過程需關注簡便計算,提升運算能力。但平均數很敏感,當數據中含有極個別特別大或特別小的數據(極端值)時,平均數就不能很好地反映一般水平,因此反映一批數據“中等水平”一般采用中位數;反映一組數據中出現次數最多的數一般采用眾數。再通過樣本估計總體,問題就迎刃而解,增強學生分析和解決問題的能力。

