面外彎曲加勁板結構受力特性探究

蔡軍 安永日 李小斌

(1.青海省公路局，青海 西寧 810008；2.貴州大學土木工程學院，貴州 貴陽 550025；3.青海交通投資有限公司，青海 西寧 810008)

隨著我國鋼橋飛速發展，橋梁鋼結構中曲線加勁板的應用越來越多。比如：主跨為550m的上海盧浦大橋、主跨為457m的柳州官塘大橋、主跨為420m的菜園壩長江大橋和主跨為450m的西江特大橋等。這些橋梁的拱肋采用了鋼箱拱，拱肋加勁板和加勁肋均為曲線形狀。另外，呼和浩特市南二環路部分立交工程、成都二環路部分匝道橋等，均采用了曲線鋼箱梁，腹板和加勁肋向橫橋向彎曲。

目前，國內外對彎曲鋼結構構造的研究，主要集中于曲線加勁板-直線加勁肋結構，對加勁板和加勁肋共同彎曲橋梁結構的研究尚屬空白。本文以菜園壩長江大橋鋼箱拱肋頂、底加勁板為研究對象，利用ANSYS有限元軟件分析了不同彎曲半徑下的結構極限承載能力。分析結果表明，向面外凹曲加勁板承載力與直線加勁板基本相當，但向面外凸曲加勁板相比直線加勁板承載力小設計中不能忽略。同時，提出了曲線加勁板-曲線加勁肋結構的極限承載力計算公式，并與有限元分析結果作了對比，結果表明所提出公式的計算結果偏于保守。

一、極限承載力理論計算方法

彎曲半徑R的加勁板結構在軸力N作用下受力模式如圖1所示，在跨中存在初始撓度e0，并對截面產生附加彎矩。壓彎構件的極限承載力可按式（1）式（2）計算：

圖1 彎曲加勁板受力示意圖

二、有限元分析模型

（一）構件基本構造

此次研究對象選用重慶菜園壩長江大橋，其橋型為主跨420m的組合式鋼構系桿拱橋，拱肋為提籃式鋼箱結構。拱軸線采用二次拋物線，計算矢高56.44m，矢跨比為1/5.67。拱肋截面如圖2所示，鋼箱拱肋橫截面為矩形鋼箱截面，高度為4m，寬度為2.4m，頂底板厚在24mm～40mm之間變化，加勁肋厚度在20mm～24mm之間變化。

圖2 鋼箱拱肋尺寸(mm)

局部模型以菜園壩長江大橋鋼箱拱肋頂板加勁板和底板加勁板為研究對象。為提高計算效率，拱軸線按圓弧線計算，計算長度取10m，將其作為基礎計算模型，具體尺寸如表1所示。

表1 曲線加勁板基本參數（m）

表1中a、b、t分別為橫隔板間距、母板寬度和厚度；hs、ts、ns分別為縱向加勁肋高度、厚度和數量；ht、tt、nt分別為橫隔板高度、厚度和數量。

加勁板彎曲半徑取值如表2所示，半徑從∞～20m分6種，彎曲形狀為向面外凸曲拱肋頂部加勁板和向面外凹曲拱肋底部加勁板。

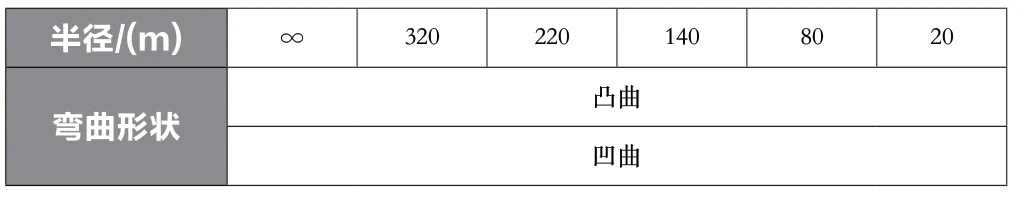
表2 分析結構類型

（二）初始幾何缺陷

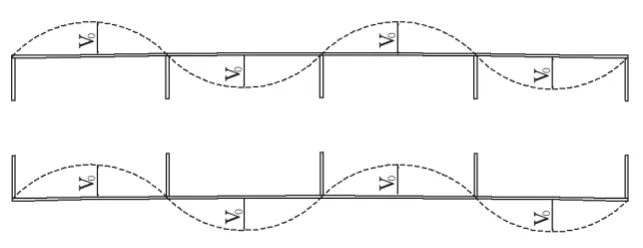
圖3 初始幾何缺陷取值示意圖

圖4 殘余應力場的簡化計算模式（mm）

有限元計算模型中，初始幾何缺陷如圖3所示，取《鋼結構設計規范》給定的最大幅值。焊接殘余應力分布情況如圖4所示，加勁板的殘余拉應力為σy，殘余壓應力為0.25σy，加勁肋殘余拉應力為σy，殘余壓應力為0.17σy 。

（三）有限元模型設計

拱肋加勁板、加勁肋、橫隔板均采用Shell181單元。鋼材應力—應變曲線如圖5所示，屈服點為345.0MPa，彈性模量為2.06×105MPa，剪切模量為0.79×105MPa，切線模量為2.06×103MPa，泊松比為0.3。邊界條件為約束母板四邊豎向位移，約束所有橫隔板底部徑向位移，約束中間橫隔板桿件方向位移和橫向位移。加載方式為加勁板及加勁肋兩端施加的均布線荷載，荷載增量采用弧長法。兩種計算模型的具體邊界條件及加載方式相同，如圖6所示。

圖5 材料本構關系

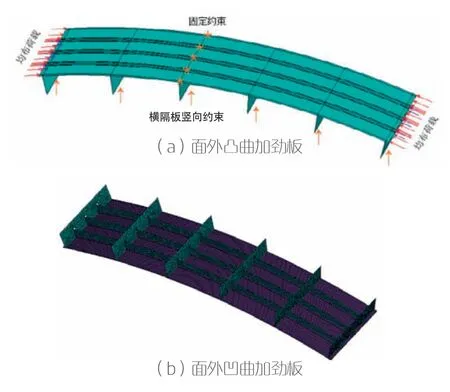
圖6 數值分析模型示意圖

三、有限元結果分析

（一）荷載—位移曲線及承載力

面外凸曲加勁板荷載—位移曲線如圖7所示，半徑越小初始剛度的降低越快，結構屈服點越低，與最大值及對應位移越小，荷載達到最大值后剛性下降越快。

面外凹曲加勁板荷載—位移曲線如圖8所示，半徑20m加勁板最大荷載明顯比其他半徑加勁板小，剛度降低、屈服點、最大值及對應位移等沒有規律。

圖7 面外凸曲加勁板荷載—位移曲線

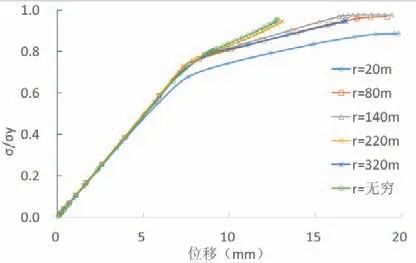
圖8 面外凹曲加勁板荷載—位移曲線

圖9 面外凸曲加勁板最大荷載時等效應力云圖（kPa）

表3 面外凸曲加勁板平均最大應力匯總結果

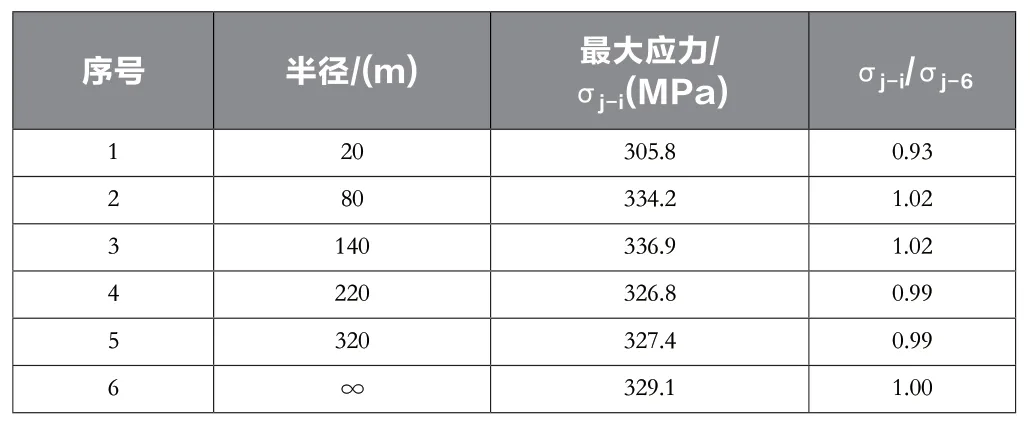
表4 面外凹曲加勁板平均最大應力匯總結果

面外凸曲加勁板平均最大應力匯總結構如表3所示，半徑∞：320：220：140：80：20m的最大承載力比值為1.00：0.92：0.91：0.90：0.87：0.77，隨著半徑變小承載力下降，并降幅均超過5%設計中不能忽略。

面外凹曲加勁板平均最大應力匯總結構如表4所示，半徑∞：320：220：140：80：20m的最大承載力比值為1.00：0.99：0.99：1.02：1.02：0.93，半徑20m加勁板承載力降幅為7%，其他誤差在2%以內，基本可不考慮彎曲影響。

（二）應力分布及變形

圖10 面外凹曲加勁板最大荷載時等效應力云圖（kPa）

面外凸曲加勁板的最大荷載時應力分布及變形如圖9所示，除了加勁板與加勁肋連接處局部區域外其他區域都已經達到屈服狀態。產生這種現象的原因在于此處由焊接而產生了初始拉應力。另外，由于硬化原因部分區域加勁肋等效應力超過屈服點，并已經發生面外屈曲。

面外凹曲加勁板的最大荷載時應力分布及變形如圖10所示，半徑80m～320m加勁板，除了加勁板與加勁肋連接處局部區域外其他區域都等效應力超過了屈服點。半徑為20m的加勁板應力略小于屈服點，在橫隔板處加勁肋等效應力超過了屈服點。

四、有限元分析結果與理論計算值對比分析

面外凸曲加勁板的有限元分析結果和理論計算值對比結果如表5所示，當彎曲半徑∞～140m誤差在5%以內，半徑小于140m則誤差偏大，并理論計算值偏于保守。產生這種現象主要原因在于壓彎構件承載力相關計算公式為簡化計算方法偏于保守。

面外凹曲加勁板的有限元分析結果和理論計算值對比結果如表6所示，理論計算值普遍大于有限元分析值，并誤差較大。產生這種現象的主要原因在于壓彎構件承載力相關計算公式偏于保守，并加勁板屈服后硬化原因等效應力已經超過了屈服值。

五、結語

本文通過彎曲半徑∞～20m的面外凸曲和面外凹曲加勁板的有限元分析和理論計算值對比，得出了以下結論：

表5 面外凸曲加勁板最大應力計算結果

表6 面外凹曲加勁板最大應力計算結果

一是面外凸曲加勁板的承載力小于直線加勁板，半徑越小降幅越大。在本文分析中彎曲半徑320m～20m的降幅達到0.08～0.23，設計中不能忽略。

二是面外凹曲加勁板的承載力在彎曲半徑320m～80m范圍內，與直線加勁板相比誤差在2%以內，基本可不考慮彎曲影響。

三是面外凹曲加勁板承載力比外凸曲加勁大，并隨著半徑減少差距變大。

四是本文中提出的理論計算方法偏于保守。