基于粒子濾波的結構參數和荷載同步識別方法

李天之，劉 綱,b，張亮亮,b

(重慶大學 a土木工程學院；b.山地城鎮建設與新技術教育部重點實驗室，重慶 400045)

結構參數和荷載的識別對結構健康監測、有限元模型更新等具有重要作用。在假設荷載已知的情況下，基于最小二乘估計[1-2]、擴展卡爾曼濾波(EKF)[3-4]、無味卡爾曼濾波(UKF)[5-7]、粒子濾波(PF)[5,8-9]等眾多時域方法被廣泛應用于非線性系統的參數識別。當已知結構參數時，可采用卡爾曼濾波[10-13]等對荷載激勵進行辨識。在土木結構服役過程中，結構參數的變化和荷載激勵往往都是未知的，將結構參數識別和荷載辨識分開進行研究較難滿足土木工程的實際需求。為解決這一難題，各國學者逐步發展了結構參數與荷載同步識別方法，丁勇等[14]運用正交分解法建立荷載方程，帶入狀態空間方程，再運用改進UKF算法識別參數和荷載，在三層非線性框架的數值模擬中，可成功識別剛度、阻尼等結構參數和隨機荷載；萬志敏等[15]在運用改進粒子濾波算法識別結構參數的同時，運用最小二乘估計求得荷載，數值模擬表明，該法同時識別參數和荷載的效果較好。以上解決方案都采用了2種不同的算法，流程相對復雜。同步識別結構參數與荷載還面臨另一個難題，當僅運用加速度進行長時間荷載識別時，其結果隨著時間的推移逐漸發生偏移，這是基于時域方法的荷載識別過程中難以避免的現象[15]。雖然可以將速度或位移作為觀測值來解決這一問題[5]，但在結構健康監測系統的實際應用中，由于較難測量結構的動態速度或位移，一般僅將加速度作為觀測值；另一種可行的方法是通過額外的步驟，如虛擬測量技術對位移進行調整[11]。

文中將結構參數、荷載、速度和位移同時作為狀態值[16]，構造狀態空間方程，采用粒子濾波算法直接對結構參數與荷載進行識別，步驟相對簡單。同時，針對荷載辨識結果漂移的問題，將加速度數據進行梯形積分和零相位高通濾波，求得速度和位移的計算值，利用計算值來更新由粒子濾波求得的速度和位移狀態值，長時間確保荷載識別的準確性。

1 狀態空間方程

一般來說，土木結構的狀態空間方程為

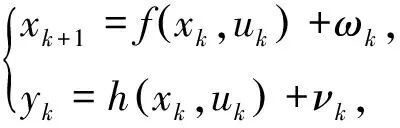
(1)

其中，xk、uk和yk分別是第k時間步的狀態值(包括位移和速度)、荷載激勵和結構響應；ωk和νk分別是第k時間步的過程噪聲和觀測噪聲；f(·)和h(·)是非線性函數，描述了狀態值和結構響應隨時間變化的關系。

為實現結構參數和荷載的同步識別，可將結構參數mk、荷載激勵uk與原有的狀態值xk組成新的狀態向量zk[16]。

(2)

新的狀態向量zk與結構響應yk組成新的狀態空間方程：

(3)

式中，θk和ηk分別是結構參數與荷載激勵的過程噪聲。文中所有噪聲均假設為零均值高斯噪聲。

2 粒子濾波與加速度更新方法

2.1 粒子濾波算法

以式(3)為例，粒子濾波的流程如下：

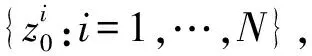
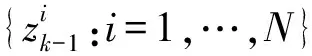
(4)

(5)

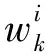
(6)

計算有效粒子數Neff：

(7)

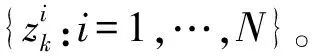
(8)

2.2 加速度更新策略

土木結構通常僅能得到加速度響應{ak:k=1,…,n}，采用梯形積分得到k時間步的速度vk：

(9)

其中，T是采樣周期。

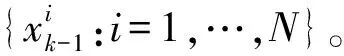
3 數值模擬

3.1 三層框架結構

采用如圖1所示的三層框架對文中方法進行驗證，每層的剛度s1=s2=s3=500 N/m，每層的質量m1=m2=m3=20 kg。通過集中質量矩陣和剛度矩陣計算得到前三階的自振頻率：f1=2.225 rad/s，f2=6.235 rad/s，f3=9.010 rad/s，假設第一階阻尼比ξ1、第三階阻尼比ξ3均為0.05，結構阻尼為瑞利阻尼，可通過式(10)求得瑞利阻尼參數為α=0.178，β=0.009。

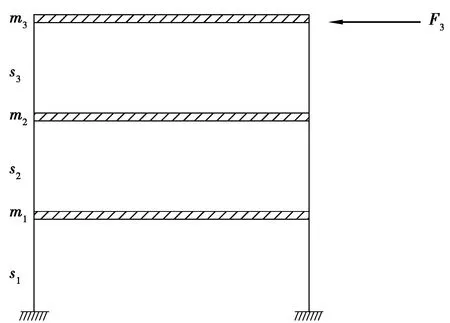
圖1 三層框架數值模擬

(10)

以NS方向的El-centro地震波生成外部荷載F3，水平作用在第三層上，最大值為34.87 N。

采樣頻率設置為200 Hz，通過Newmark-β法計算得到結構前30 s的加速度數據。假定觀測噪聲是零均值高斯噪聲，其標準差為加速度響應數據的5%均方根值。計算所用的荷載及各層加速度如圖2所示。

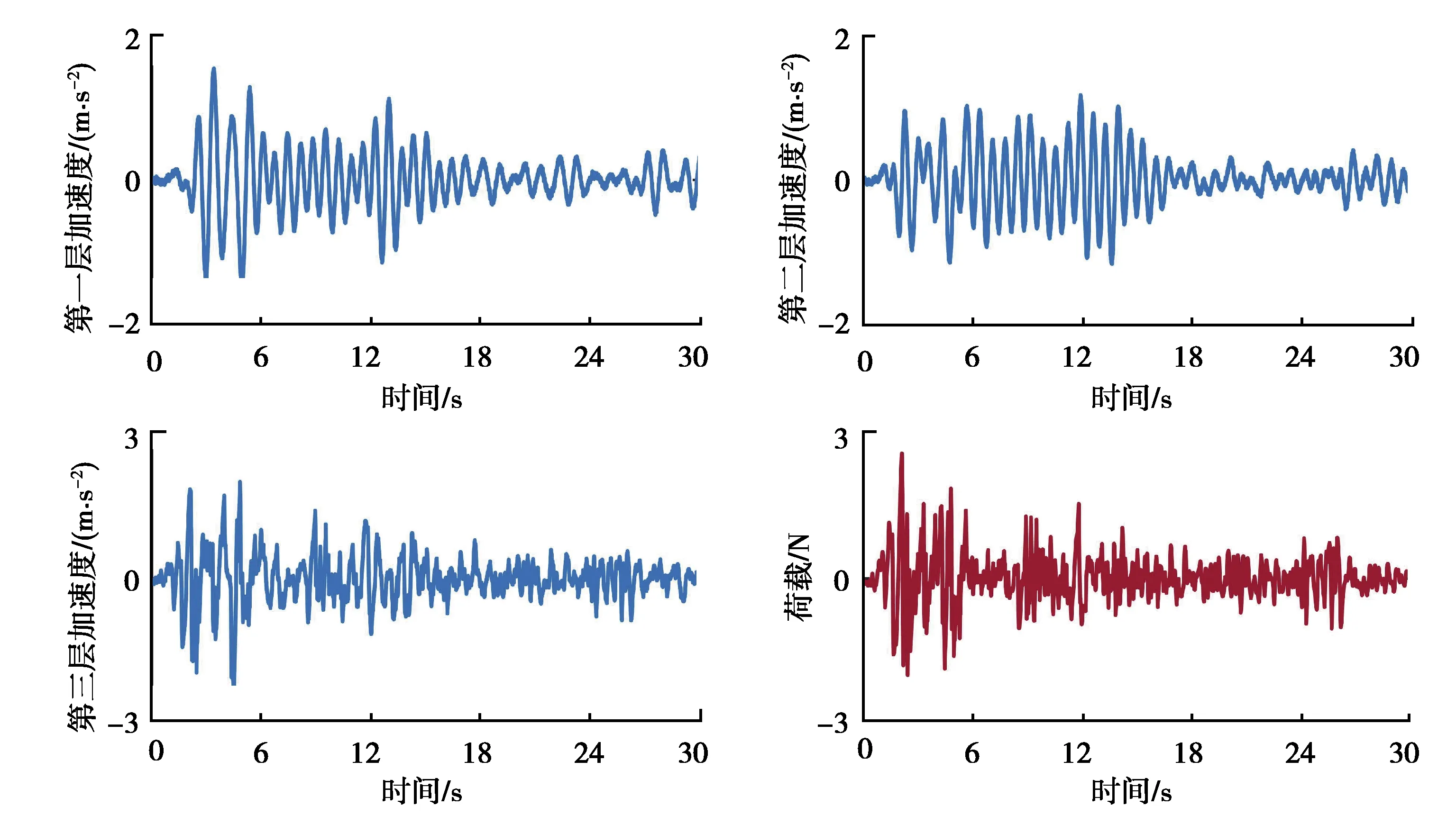
圖2 加速度與外部荷載

3.2 框架結構的狀態空間方程

圖1所示三層框架結構的動力學方程為

(11)

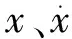
當對結構剛度、荷載同時進行識別時，公式(11)可轉換為離散化的狀態空間方程[5]：

(12)

其中，{ωi:i=1,…,6}、{θi:i=1,2,3}和η是過程噪聲，{υi:i=1,2,3}為觀測噪聲，T=0.005 s。圖1中的三層框架是線性結構，由于式(12)中存在未知參數與未知速度、位移相乘的情況，該公式是非線性方程[5,9]，故采用粒子濾波進行參數識別。

運用梯形積分和截止頻率為0.1 Hz的零相位高通濾波，可通過加速度求得速度、位移計算值。在此數值模擬中，取Δt=1 s，即每隔1 s對速度、位移狀態值進行調整。在粒子濾波算法中，重采樣的閾值NT取0.5，粒子個數N=16 000。初始剛度在400～800 N/m的范圍內隨機取值，荷載、位移和速度的初始值均取0。假設各過程噪聲均為獨立的零均值高斯噪聲，根據試算，速度、位移的過程噪聲的標準差分別取速度、位移計算值的0.2%均方根值，剛度、荷載的過程噪聲的標準差分別取0.1、2.5。

3.3 識別結果分析

分別將不調整速度、位移狀態值以及按文中方法進行調整后的結果繪制于圖3中，其縱坐標代表在16 000個粒子中剛度或荷載的均值。

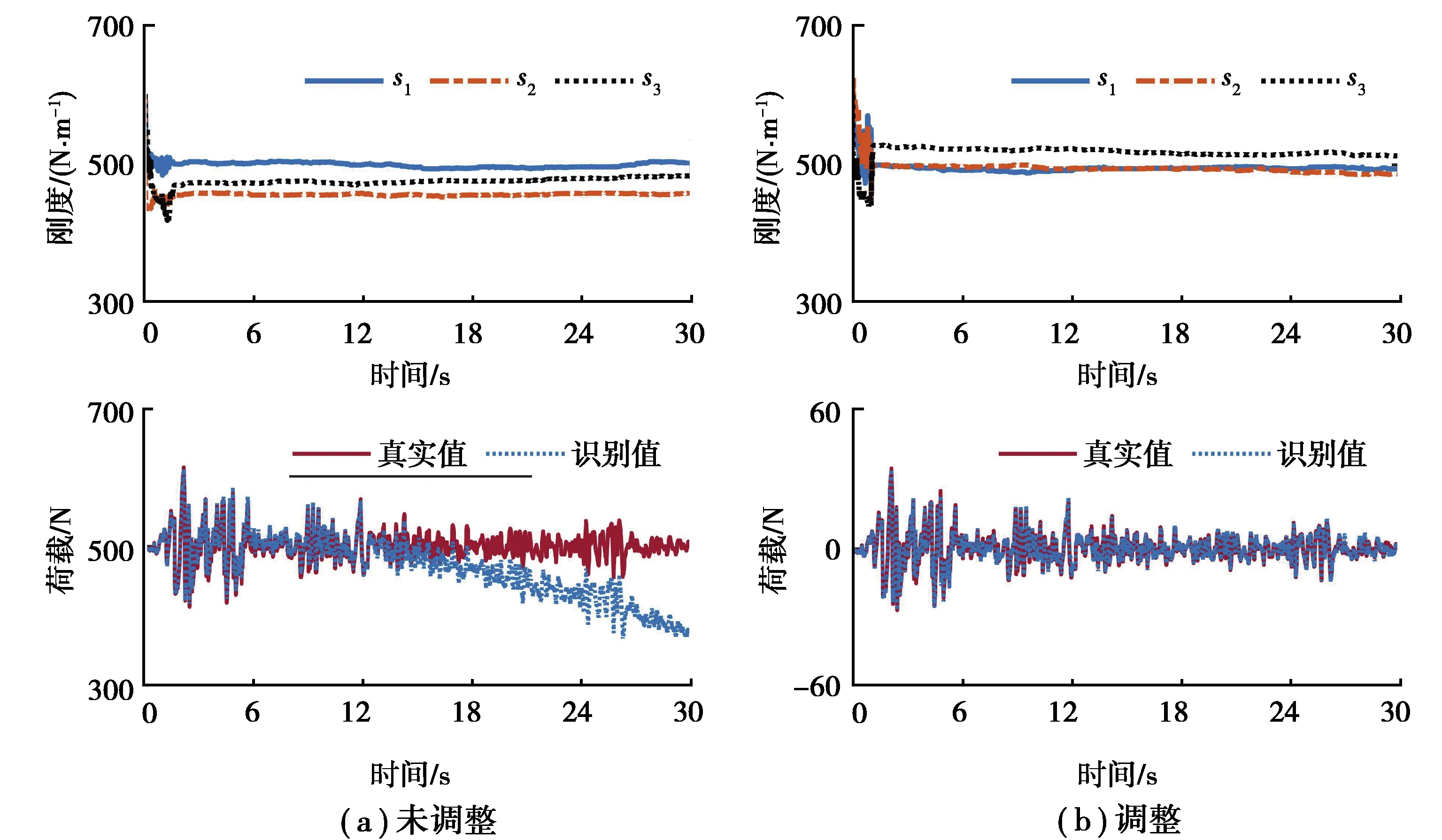
圖3 結構參數與荷載辨識過程

將最后一步的均值作為參數識別結果，并用相對誤差(RE)來評價各參數識別結果的精度：

(13)

其中，se表示剛度識別結果；sr表示剛度真實值。

用均方誤差(MSE)來評價荷載識別的精度：

(14)

其中，Fe(k)表示第k步的荷載識別值；Fr(k)表示第k步的荷載真實值；M是時間步長。

由圖3(a)和表1可知，當不調整速度、位移狀態值時，1.5 s左右結構參數收斂，識別結果較好；但在大約10 s后，荷載辨識值發生漂移，程度越來越嚴重。此時，剛度識別值已接近真實值，故剛度值的辨識誤差不是荷載出現漂移的原因。正如文獻[11]所述，這是僅用加速度數據進行長時間荷載辨識過程中難以避免的現象。從圖3(b)和表1可知，對結構參數而言，文中方法的參數識別收斂時間、精度和傳統方法基本一致；但對于荷載識別而言，全過程中未出現漂移現象，有效解決了傳統方法的不足。

表1 參數識別和荷載識別結果

由于初始值、噪聲的影響，識別結果具有一定的隨機性，在同樣的情況下再對同一組數據進行9次識別，計算結果如表2所示。從表2可知，結構參數識別的最大誤差為-14.60%，最小誤差為0.26%；荷載激勵識別的最大均方誤差為1.88，最小均方誤差為0.79。

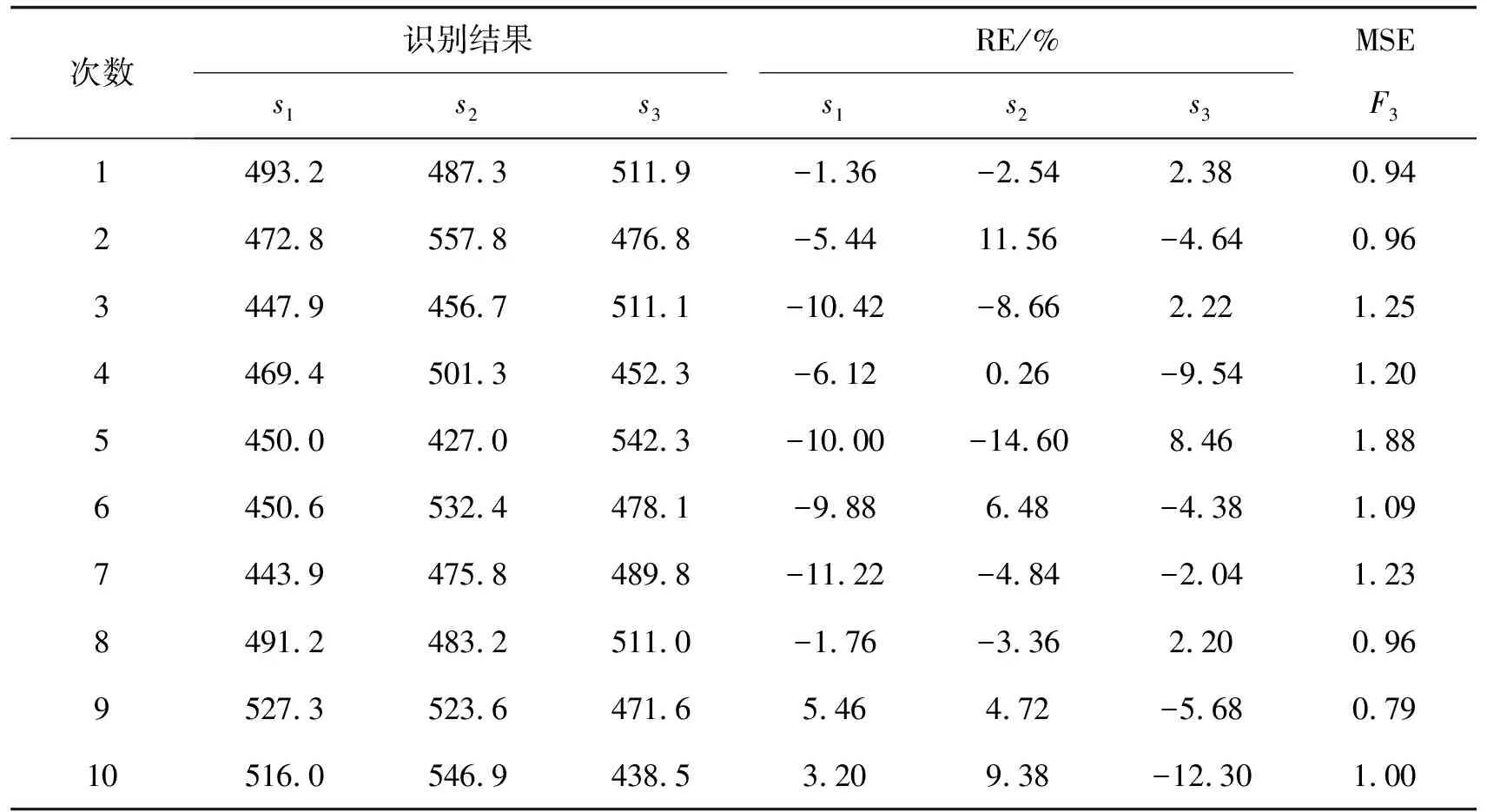
表2 結構參數與荷載10次同步識別的結果

3.4 調整時間間隔對識別的影響

為研究調整時間間隔Δt對結構參數、荷載識別的影響，選取{Δt=0.1, 0.3, 0.5, 1, 1.5, 2, 3}共7種情況各進行10次運算，不同Δt時的參數相對誤差的絕對值的均值、10次荷載識別均方誤差的均值如圖4所示。

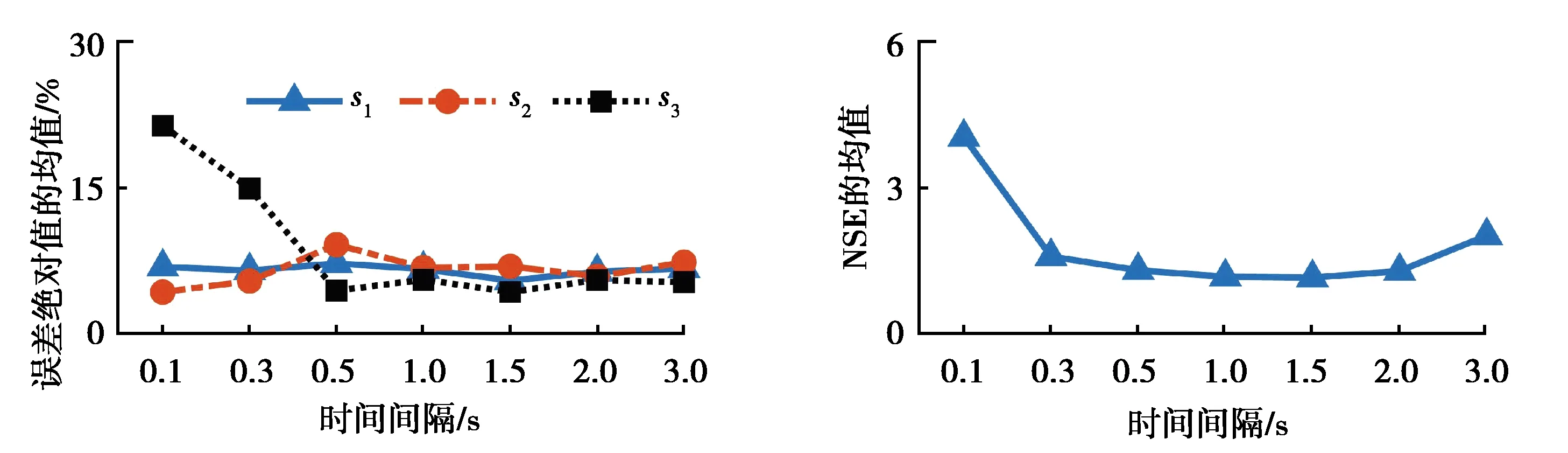
圖4 不同時間間隔Δt的識別情況

由圖4可知，當Δt較短(如0.1 s、0.3 s)時，第3層的剛度s3的誤差和荷載識別的均方誤差相對較大。因為在該時段內結構參數識別尚未收斂，此時用帶有誤差的速度、位移計算值來調整狀態值，參數識別受到的影響相對較大；同時，誤差相對較大的s3會對荷載識別造成影響。隨著Δt逐漸增大，各剛度識別的誤差基本保持不變，但荷載識別的均方誤差會逐漸增大。各參數趨于收斂或已收斂，計算值的誤差對參數識別的影響相對較小；同時，由于不能及時修正速度和位移，荷載識別值會逐漸漂移，故其均方誤差會隨時間間隔的增大而增大。綜上所述，為同時保持結構參數和荷載識別的精確性，應合理設置Δt，不宜過長或過短，建議以參數收斂所需的時間(數值模擬算例的1.5 s)來設置間隔Δt。

4 結束語

為了土木工程結構不僅能測試結構的加速度響應，同時還能識別結構參數和輸入荷載，文中將結構參數和荷載擴充為狀態值并建立狀態空間方程，基于粒子濾波算法進行結構參數和荷載的同步識別。同時，利用測試的加速度響應，通過梯形積分和零相位高通濾波計算各時間步的速度、位移，然后將該值以一定時間間隔Δt用于更新對應狀態識別值。三層框架結構的數值算例結果表明：

1)文中方法可同時識別結構參數與荷載，識別結果較為準確、穩定。

2)采用積分和零相位高通濾波所得的速度、位移計算值來調整速度、位移狀態值可克服荷載辨識值出現偏移這一問題。

3)應合理設置速度、位移的時間間隔Δt，不宜過長或過短，建議根據結構參數識別收斂所需的時間來設置Δt的大小。