辦公建筑運行能耗的混沌時間序列復合預測

于軍琪，段佳音，趙安軍，井文強，王佳麗

(西安建筑科技大學 建筑設備科學與工程學院，西安 710055)

辦公建筑在全生命周期中普遍存在能耗大、能效低等問題，導致嚴重的能源浪費。其節能潛力巨大，降耗幅度可以達到30%～50%[1]。其中，辦公建筑運行能耗占比最大。因此，研究辦公建筑的運行能耗情況具有重要意義，對其進行實時準確地預測可以為優化運行效率提供數據決策，從而實現節能目標。

建筑能耗的預測方法主要分為兩大類：正演模型和數據驅動模型。筆者根據獲得的辦公建筑歷史能耗數據特點，利用數據驅動模型中的時間序列法進行能耗短期預測。機器學習預測方法是最常用的短期能耗預測方法，已經廣泛應用于風速預測[2]、電力需求預測[3]、建筑能耗預測[4]、建筑冷負荷預測[5]等能源領域。目前國內外建筑能耗時間序列預測方法應用較為廣泛的有：人工神經網絡[6](ANN, artificial neural network)、差分整合移動平均自回歸[7](ARIMA, autoregressive integrated moving average)、支持向量回歸[8](SVR, support vector regression)、多元線性回歸[9](MLR, multiple linear regression)等。辦公建筑除了室外氣象參數和圍護結構等本體能耗外，還有機電設備、節假日、人員占用率等復雜的運行能耗，造成其能耗時間序列具有非線性特征。為了深入挖掘其時間序列內部的非線性規律，提高預測精度，研究者們將不同的算法與人工神經網絡和支持向量機結合，建立了多種辦公建筑混合預測模型。文獻[9]根據天氣、人員等多種因素利用MLR方法對辦公建筑的逐日冷負荷進行了回歸預測，與實際負荷相比平均絕對百分誤差小于8%。文獻[10]利用反饋神經網絡(BPNN, back propagation neural network)，徑向基函數神經網絡(RBFNN, radial basis function neural network)，廣義回歸神經網絡(GRNN, generalized regression neural network)，支持向量機(SVM, support vector machine)方法分別對辦公建筑的逐時能耗進行分析，以中國廣州某辦公樓為實例，取得了較好的預測效果。文獻[11]建立了小波-支持向量機(wavelet-SVM)，小波-偏最小二乘-支持向量機(Wavelet-PLS-SVM, wavelet-partial least squares-support vector machine)模型對辦公建筑的逐時能耗進行了分析，最終得出1 h，2 h，3 h和24 h的預測結果。在其他應用領域[12]將平均速度、平均占有率和平均交通流時間序列利用貝葉斯理論集成到一個時間序列中，將混沌理論和SVR相結合用于交通流的時間序列預測，達到了較高的預測精度。上述研究都是基于多變量輸入的，相較于單變量時間序列需要考慮的因素復雜，文獻[13]使用歷史時刻的辦公建筑冷負荷根據貝葉斯理論映射到同一時間維度作為機器學習預測模型的單變量輸入，利用Chaos-SVR和WD-SVR(wavelet decomposition-support vector regression)分別對建筑冷負荷時間序列進行預測，結果表明，Chaos-SVR效果更優。因此，選擇恰當的預測模型不僅可以避免單變量輸入的局限性，而且會取得較好的預測效果，但由于組合模型在迭代過程中存在誤差累積的問題，導致不能很好地滿足實際優化運營的需求。

為了解決以上問題，筆者探究了混沌現象背后隱藏的決定性規律使得將混沌理論應用于辦公建筑運行能耗預測領域的可能性，展開了以下研究工作：

1)分析辦公建筑運行能耗的特點及構成，進行數據預處理和時間序列的混沌特性判別。

2)將混沌理論(Chaos theory)和支持向量理論結合，構建Chaos-SVR辦公建筑能耗預測模型。

3)利用Markov鏈修正Chaos-SVR組合模型中由于參數傳遞存在的累積誤差。

4)以西安某辦公建筑監測數據為例進行實例分析，并與其他預測方法進行比較，驗證了模型的有效性。

文中主要研究辦公建筑運行能耗的混沌特性，其他大型公共建筑比如商業建筑、醫療建筑等能耗是否具有混沌特性，模型的可推廣性將是下一步的研究重點。

1 能耗數據特征分析

辦公建筑能耗混沌時間序列預測研究的前提是確定該時間序列具有混沌特征[14]。文中通過西安市建筑能耗監測平臺，采集某辦公建筑2019年8月1日0點到9月30日23點各項分類能耗數據，如表1所示。

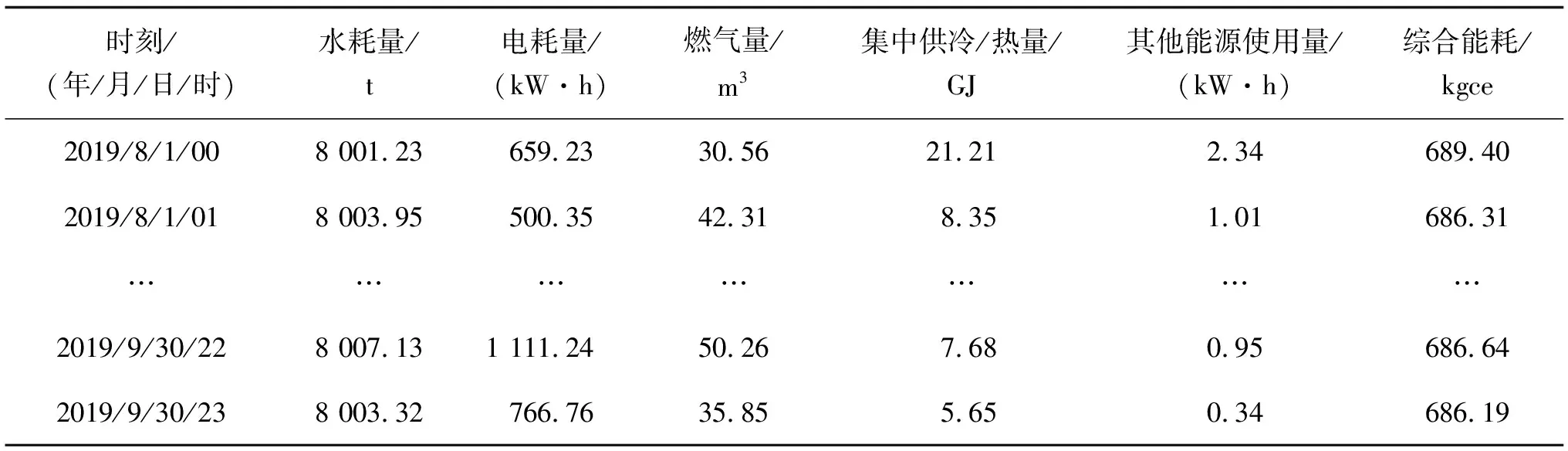
表1 西安某辦公建筑能耗量統計

從表1可以看出，辦公建筑運行能耗包括水耗量、電耗量、燃氣量、集中供冷/熱量和其他能源使用量。為了對辦公建筑運行能耗時間序列進行混沌特性分析，由于其組成結構復雜，需要對多項數據統一量綱。因此，將所有運行能耗的量綱轉化為千克標準煤(kgce)的形式，從而得到該辦公建筑運行能耗的逐時序列。然后對該逐時序列數據進行處理，利用最大 Lyapunov指數法來判斷其是否具有混沌特性。最大Lyapunov指數法是基于相空間重構的，因此對時間序列進行相空間重構是研究的前提。

1.1 相空間重構

相空間是一種工具，用于描述由確定自由度的確定性混沌系統生成的單變量或多變量時間序列重構的動態系統[15]。相空間重構的主要原理是在拓撲等價意義下從高維空間中恢復混沌吸引子的動力學特性[15]，對于總能耗的逐時時間序列x1,x2,x3,…,xn-1,xn，適當選取嵌入維數m和延遲時間τ，得到重構相空間

Ym(i)=[x(i),x(i+τ),x(i+2τ),…,x(i+(m-1)τ)]，

(1)

式中，i=1,2,…,n;N=n-(m-1)τ。N表示由時間序列構成m維后，由n個相點變成了N個相點。

嵌入維數和延遲時間的合理選取決定了辦公建筑能耗時間序列相空間重構的質量，同時也保證了在實際預測中有足夠高的預測精度。研究表明[16]，將τ和m聯合起來的嵌入窗寬的確定也會影響重構相空間的質量。C-C[17]法通過序列的關聯積分來構成統計量，通過統計量和延遲時間的關系圖同時計算出延遲時間τ和最佳窗寬[16]τw，再根據τω=(m-1)τ求出嵌入維數。該方法既能有效地減少互信息量法的計算量，又能保持時間序列的非線性特征。故本文采用C-C法求取延遲時間和嵌入維數，具體步驟如下：

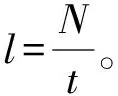
(2)

式中，dij=‖Xi-Xj‖，Xi為相空間的點，θ(·)為階躍函數：

(3)

2)統計量代表了非線性時間序列的相關性。通過時間序列的關聯積分來構成每個不相交的時間子序列的檢驗統計量：

(4)

令n→∞，則：

(5)

3)如果時間序列是獨立同分布的，對于固定的m和t，當N→∞時，r取任意值時，S(m,r,t)恒等于零。但實際的時間序列是有限的，因此一般S(m,r,t)不等于零。那么，局部最大時間間隔可以取S(m,r,t)的零點或對所有的半徑r相互差別最小的時間點，這意味著這些點幾乎是均勻分布的。選擇對應值最大和最小的2個半徑r，定義關于r的最大偏差：

ΔS(m,t)=max{S(m,rj,t)}-min{S(m,rj,t)}。

(6)

局部最大時間t應該是S(m,r,t)的零點和ΔS(m,t)的最小值。但是S(m,r,t)的零點對所有m,r應幾乎相等；ΔS(m,t)的最小值對所有m應幾乎相等。延遲時間τ對應著這些局部最大時間t中的第一個。

4)通過統計量和延遲時間的關系圖來確定τ和嵌入窗寬τω，從而確定出嵌入維數[16]。

幾種重要漸進分布的數學統計結果表明：當2≤m≤5,σ/2≤r≤2σ,N≥500時(σ指時間序列的均方差或標準差)，漸近分布可以通過有限序列很好的近似，S(m,n,r,1)能代表序列的相關性。具體計算時，根據辦公建筑能耗時間序列特性，取m=2,3,4,5,ri=iσ/2,i=1,2,3,4,相點數n=3 000，計算下列3個檢驗統計量[17]：

(7)

(8)

(9)

根據上述計算結果在MATLAB中繪制圖像，得到C-C法重構辦公建筑能耗時間序列統計量曲線如圖1所示。

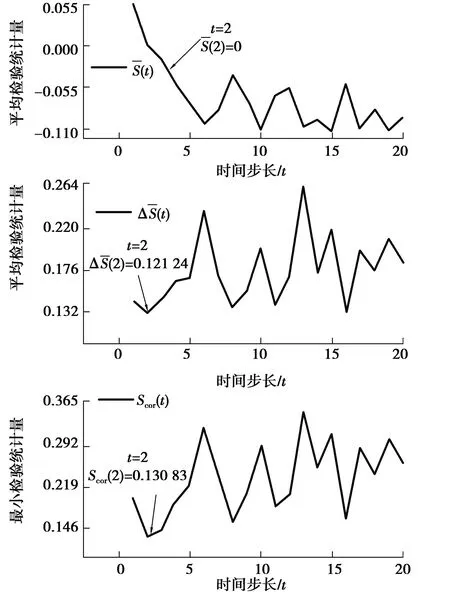
圖1 C-C法重構辦公建筑總能耗時間序列統計量曲線圖

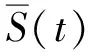
因此，該辦公建筑總能耗時間序列重構的相空間為Y2(i)=[x(i),x(i+2)]。

1.2 混沌特性判別

一個系統的Lyapunov指數譜中有一個或一個以上的正值就可以肯定其存在混沌特性[18]。在相空間重構后，相空間中的兩條相鄰軌線將隨時間逐漸發散或聚合，而Lyapunov指數是其軌線的收斂或發散率，正的最大Lyapunov指數反映時間序列具有混純特征，負的最大Lyapunov指數表明時間序列具有隨機性或周期性。最大Lyapunov指數越大，時間序列的非線性越強，對初值越敏感[18]。

小數據量法[19]可以充分利用所有能夠利用的數據，對小數據組來說比較可靠，計算量不大，相對容易操作，計算結果精度高。因此采用小數據量方法計算最大Lyapunov指數。小數據量法求取最大Lyapunov指數的步驟如下：

1)平均周期是從相空間的意義上度量一個吸引子全局屬性的最小單元，利用快速傅里葉變換得到頻譜信息，計算出能耗的平均頻率根據其倒數估算出時間序列的平均周期τp。

經過傅里葉變換后，平均周期可表示為

(10)

式中：fi(i=1,2,…L)是0 Hz和奈奎斯特頻率之間均勻分布的頻率點；Pi是在頻率點fi處的幅值。用C-C法計算出延遲時間τ和嵌入維數m。對于辦公建筑能耗時間序列{xi}，重構后的相空間為式(1)。

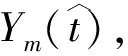
(11)

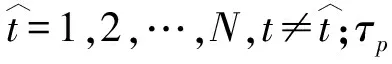
3)根據相空間中每個點的最鄰近點的平均發散速率估計最大Lyapunov指數為

(12)

式中：Δt為樣本周期。對相空間中的每個點Ym(t)，計算出該鄰域點經過i個離散事件步長后的距離

(13)

估計得到：

Lt(i)=Cjeλ(iΔt)，Cj=Lt(0)。

(14)

最大Lyapunov指數的幾何意義是量化初始閉軌道的指數發散和估計系統的總體混沌水平的量[11]，對式(14)兩邊取對數得到

lnLt(i)=lnCj+λ(iΔt)(i=1,2,…N)。

(15)

4)對每個i求出所有t的lnLt(i)平均值y(i)，即：

(16)

式中：q是非零Lt(i)的數目。最大Lyapunov指數相當于式(15)直線的斜率，可以通過最小二乘法逼近這條直線得到。

根據相空間重構C-C法求出的最佳延遲時間τ=2及嵌入維數m=2，利用小數據量法計算得出如圖2所示辦公建筑能耗時間序列的最小二乘法擬合直線。

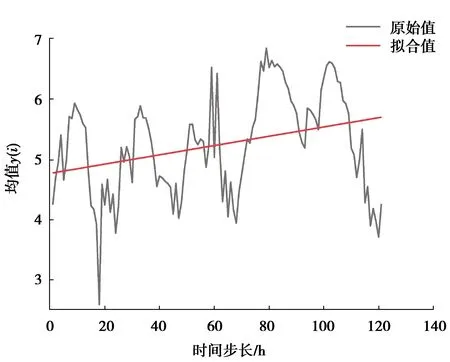
圖2 最小二乘法擬合直線

根據直線斜率可以得到最大Lyapunov指數值為0.007 7，此為正值，由此可得出辦公建筑總能耗量時間序列具有混沌特性。

2 Chaos-SVR組合模型預測

辦公建筑的Chaos-SVR的預測方法主要運用混沌理論，構造非線性映射利用相空間重構技術將原始時間序列數據所隱含的信息進行還原重構，并將其作為SVR模型的輸入，進行非線性訓練和預測。基于辦公建筑能耗的Chaos-SVR時間序列模型建立及預測過程如下：

1)構建預測模型結構，主要包括3部分：輸入向量、支持向量的非線性變化和輸出。西安某辦公建筑運行能耗的時間序列進行重構后的相空間為Y2(i)=[x(i),x(i+2)]，相點數為N=n-2，每個相點包含了每個序列的主要特征，能夠逼近建筑能耗的真實狀態。向量xi=(xi,l)是模型的輸入向量，β=(β1,β2,…βl)是輸出的權重向量，yi=f(xi)是模型的輸出。Chaos-SVR模型結構如圖3所示。

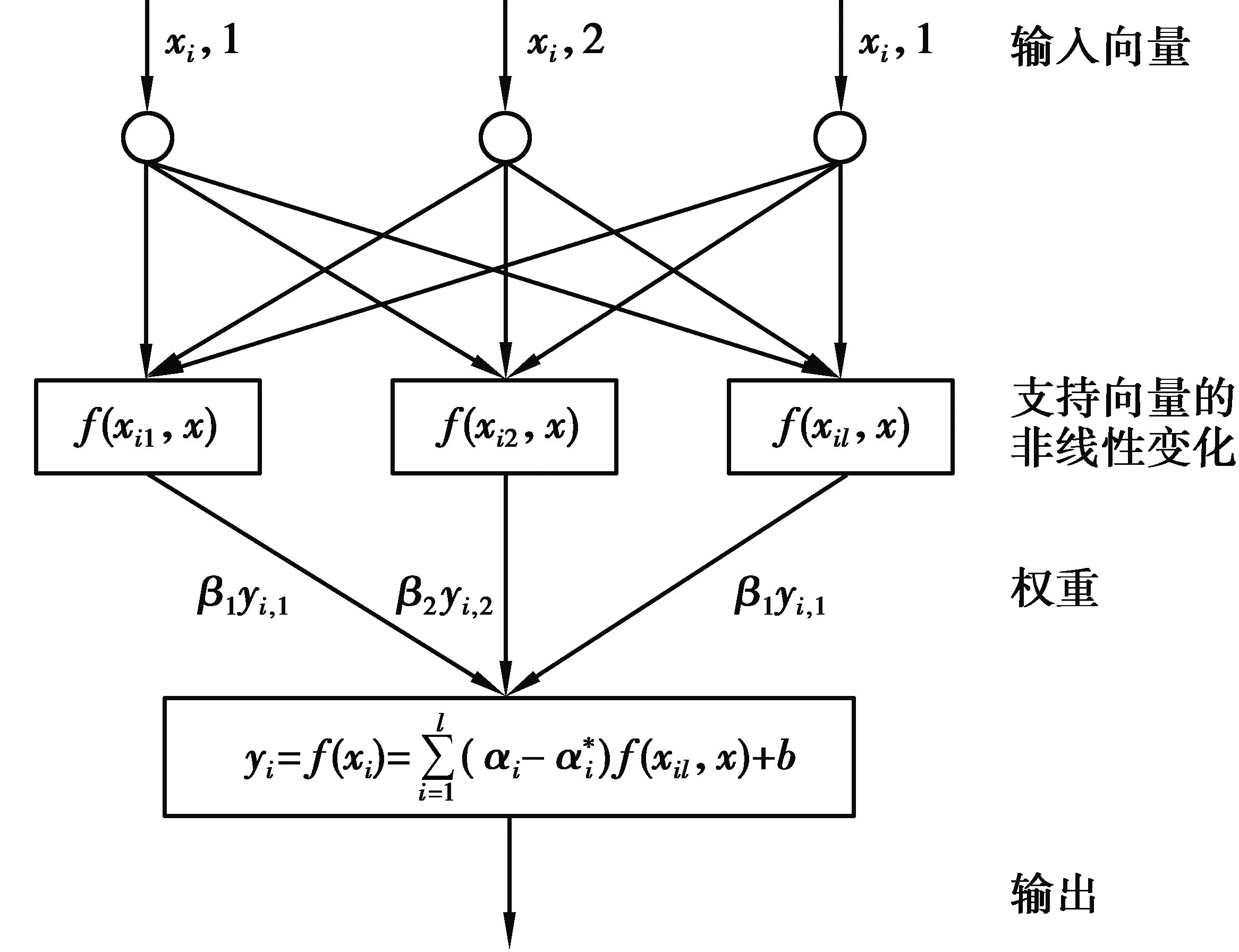
圖3 Chaos-SVR模型結構圖

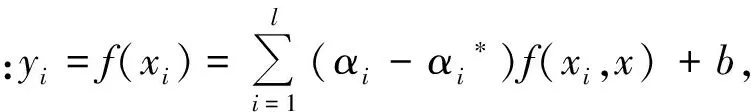
3)進行網絡循環學習，修正SVR的輸出及權值，直到誤差控制在允許范圍或迭代次數達到上限，訓練結束。

4)取樣本前n個數據之后連續的Q個數據點作為預測數據。對模型進行預測，網絡的輸出值即為預測值，將預測值進行相應的反歸一化處理，得到預測的實際值。

為了驗證模型的有效性，選取2019年9月4日～9月24日共計20天480組數據作為訓練數據，以9月25日和26日2天共計48組數據作為預測數據來進行模型驗證。并與目前在時間序列預測領域應用廣泛的2種機器學習方法——非線性自回歸神經網絡(nonlinear auto regressive neural network)和支持向量回歸(SVR)方法的預測值和實際值進行比較，利用均方根誤差RMSE(root mean squared error)平均絕對百分比誤差MAPE(mean absolute percent error)作為評價指標。預測對比結果如圖4所示。

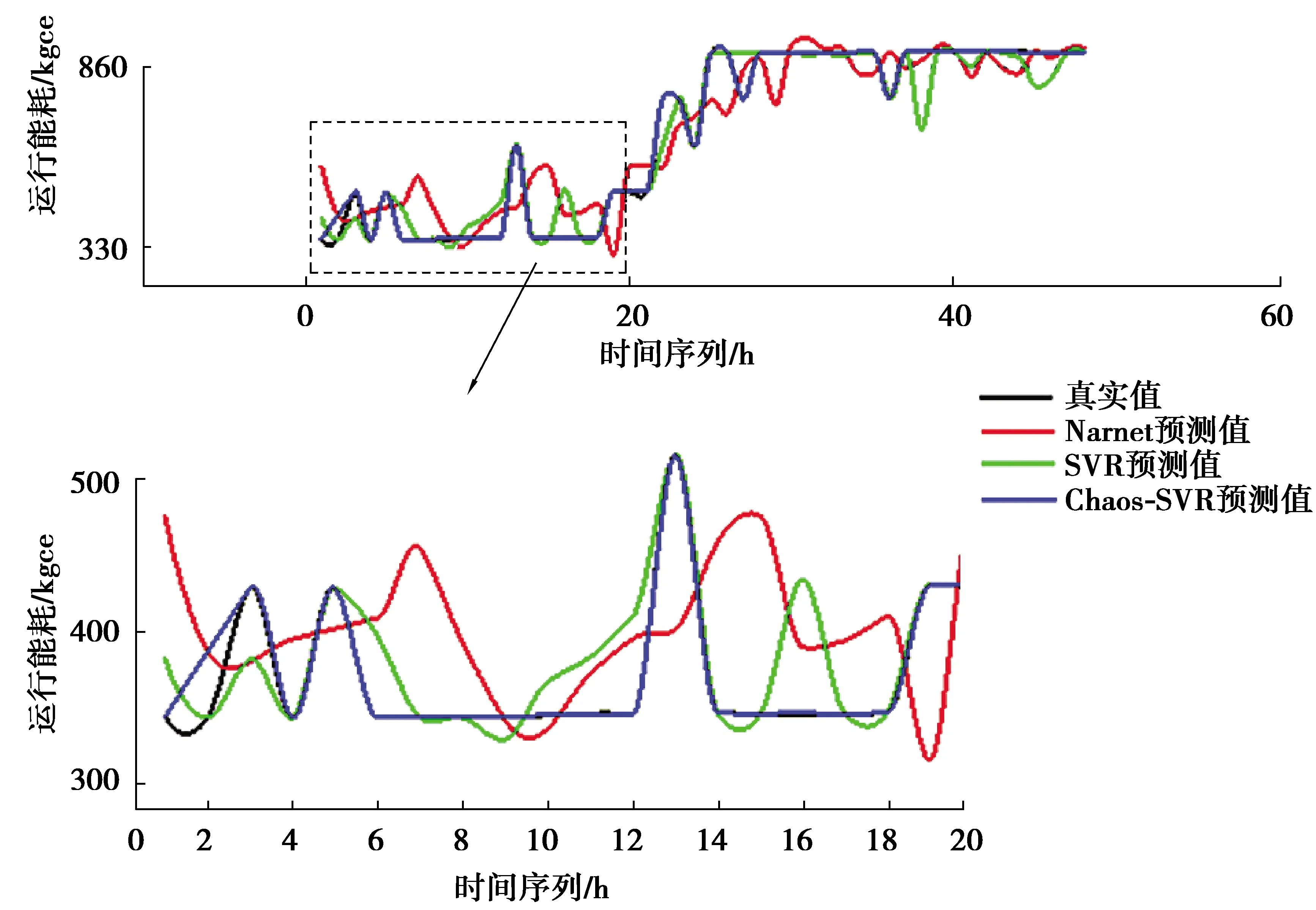
圖4 預測結果對比圖

預測結果誤差對比如圖5所示。

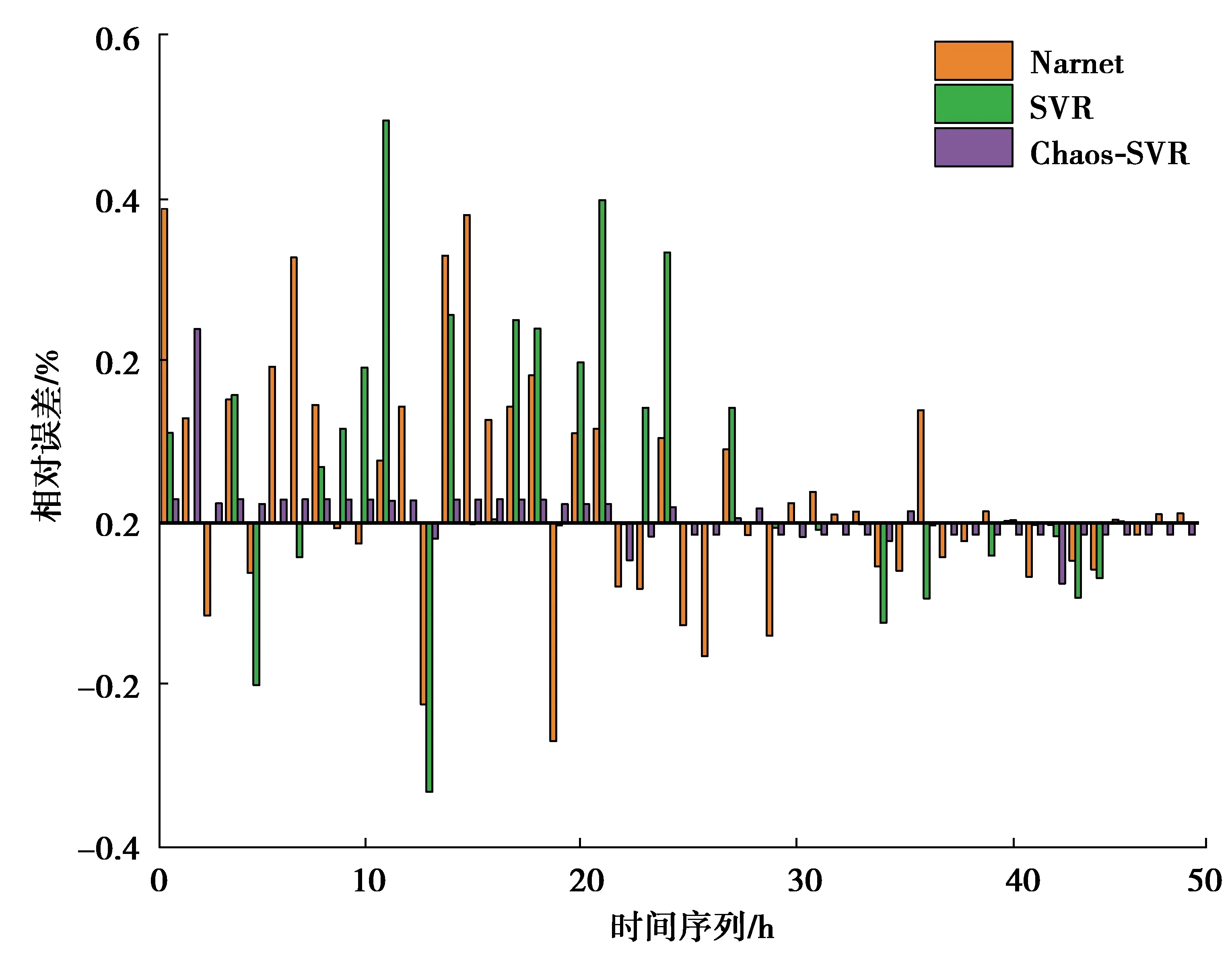
圖5 預測結果誤差對比圖

預測結果誤差如表2所示。

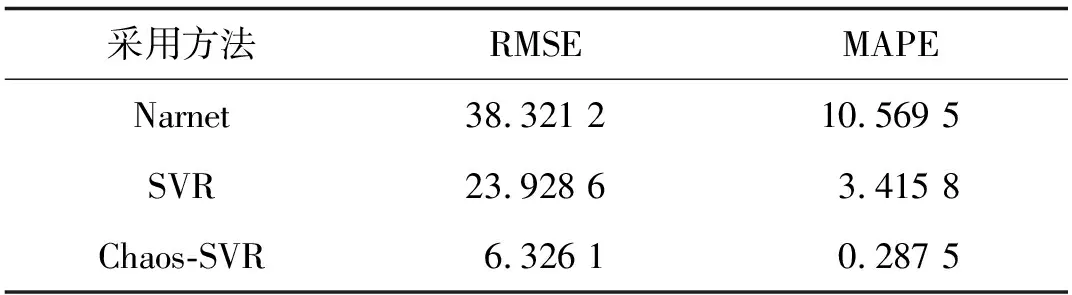
表2 預測模型誤差值

從圖4中可以看出，Narnet預測曲線波動最大，SVR預測曲線較為平緩，Chaos-SVR預測曲線距離真實值曲線最接近，部分值幾乎完全擬合。由圖5得，Narnet預測方法誤差最大，SVR預測方法誤差較大，Chaos-SVR預測方法誤差在0值附近小范圍浮動。由表2可以看出，Chaos-SVR預測模型的RMSE為6.326 1，MAPE為0.287 5，相較于其他2種方法均最小。實驗是在同樣的環境和同一組數據的基礎上進行的，Chaos-SVR預測方法相較于Narnet和SVR方法，預測效果最好，預測精度明顯提高。但Chaos-SVR組合模型在預測的過程中，還有部分值存在較大的相對誤差，為了更加精確地進行辦公建筑運行能耗預測，需要對這部分的誤差進行修正。導致這種誤差存在的原因可能是由于組合模型在迭代過程中，由于參數傳遞而出現的過程誤差積累，這樣的誤差積累會造成預測效果存在一定的缺陷。為了進一步提高預測精度，文中利用Markov鏈進行修正。

3 Markov鏈修正誤差

Markov鏈是一種具有無后效性的隨機過程[20]，Markov鏈適用于對存在波動性的預測問題進行修正描述[21]。它可以根據某一已知條件的時刻條件下推求出下一時刻的概率分布，得到下一時刻的狀態而與其他時刻無關。因此，在傳統Chaos-SVR預測模型基礎之上利用Markov鏈對累積誤差進行修正，從而實現辦公建筑能耗時間序列的精確預測。

1)誤差狀態區間[22]劃分。

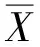
(17)

(18)

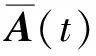
2)狀態轉移概率矩陣。

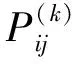
(19)

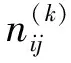
(20)

使用C-K方程(切普曼-柯爾莫哥洛夫方程)計算k步的轉移概率矩陣為

P(k)=(P(1))k。

(21)

3)預測模型。

設初始向量為P(0)，經k步轉移后的狀態向量為

P(k)=P(0)×P(k)=P(0)×(P(1))k，

(22)

據此可以判斷k步所處的狀態空間。

4)根據步驟2)所得概率轉移矩陣和步驟3)所得狀態向量，得出誤差修正后的值。

根據劃分的狀態區間對Chaos-SVR模型預測值的誤差值進行狀態劃分，劃分結果如表3所示。

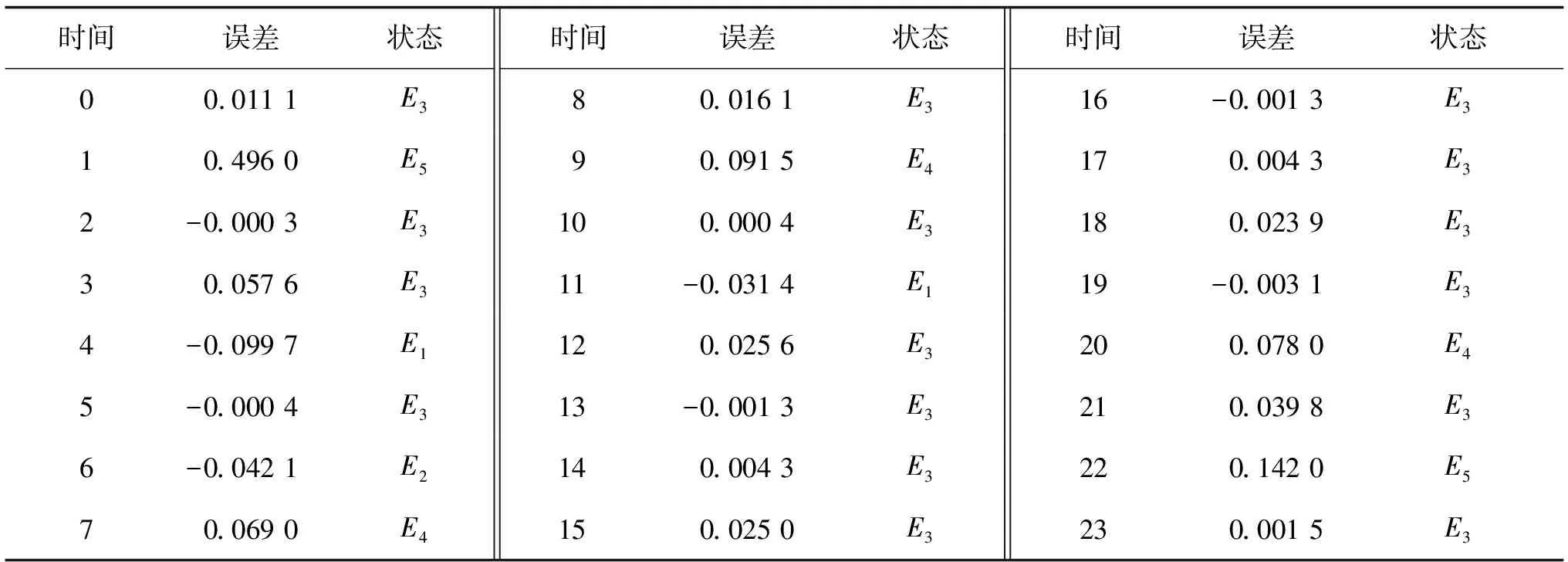
表3 Chaos-SVR模型預測誤差分類結果

根據上述誤差狀態區間的確定可以得到Chaos-SVR預測結果的Markov鏈的狀態轉移情況，進一步計算出狀態轉移概率矩陣P為

(23)

根據Markov鏈預測模型得到辦公建筑9月25日的能耗預測狀態向量，針對Chao-SVR預測模型存在的累積誤差進行修正，得到該辦公建筑能耗的最終預測值。為了驗證基于Markov鏈修正后的Chaos-SVR預測效果，對修正前后的預測結果進行比較。對比結果如圖6所示。

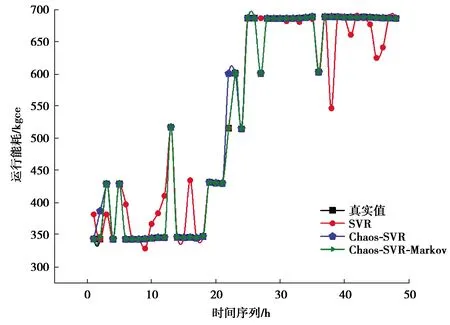
圖6 Markov修正前后預測結果對比圖

Markov鏈修正前后預測結果誤差對比如圖7所示。

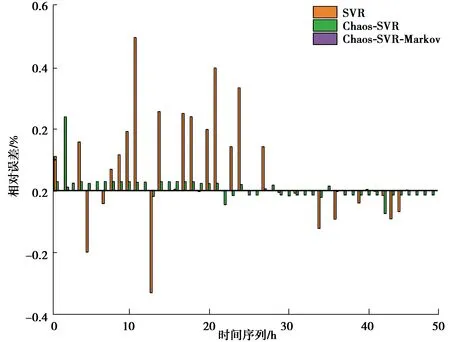
圖7 Markov鏈修正前后預測結果誤差對比圖

Markov鏈修正前后的誤差計算結果如表4所示。

表4 Markov鏈修正前后誤差值

由圖6得，經Markov修正后的模型預測曲線和真實值曲線擬合度很高，直觀地可以看到主要對2個時間點的運行能耗值進行了修正。從圖7預測結果誤差對比中可以得到證實，經過Markov鏈修正之后得誤差非常小，不僅對部分累積誤差進行修正接近于0值，其他誤差也進行了相應修正，總體預測精度顯著提高。由表4可以看到，經Markov修正之后的RMSE和MAPE均降低，這說明經過Markov鏈對組合模型中參數傳遞存在的累積誤差進行了有效改進，它的修正過程適用于辦公建筑運行能耗這一非線性系統。Markov鏈的無效性特征在組合模型的誤差修正中得到了充分體現，只對最后的預測結果做處理而不影響傳統預測模型的運算過程，更符合實際辦公建筑運行能耗的變化規律。因此，與Chaos-SVR時間序列預測模型相比，基于Markov鏈修正的Chaos-SVR時間序列預測模型更優良。

4 結 論

針對辦公建筑運行能耗預測問題，本文根據混沌理論構造非線性映射對辦公建筑運行能耗時間序列進行相空間重構，提出Chaos-SVR的組合預測模型，并利用Markov鏈對組合模型中累積誤差進行修正的方法。并將預測模型應用于西安某實際的辦公建筑，得出以下結論：

1)用C-C法求解辦公建筑總能耗時間序列嵌入維數和延遲時間，對其進行了相空間重構。同時根據小數據量法求解最大Lyapunov指數值為0.007 7，由此判定辦公建筑能耗時間序列存在混沌特性。

2)將常用的預測方法比如Narnet,SVR與本文所建立方法Chaos-SVR預測結果進行比較，本文所建立方法預測誤差最小，RMSE為6.326 1，MAPE為0.287 5，利用Markov鏈對組合模型累積誤差修正之后的RMSE和MAPE分別降為0.565 5和0.044 1。結果表明，Markov修正之后的預測精度顯著提高，為辦公建筑的優化運營與節能管理提供充分的決策依據，符合工程實際應用。