基于最小范數優化交錯網格有限差分系數的波動方程數值模擬

唐 超 文曉濤*② 王文化

(①成都理工大學地球物理學院，四川成都 610059；②成都理工大學地球勘探與信息技術教育部重點實驗室，四川成都 610059)

0 引言

波動方程正演模擬是研究全波形反演及逆時偏移技術的基礎。目前常用的波動方程數值模擬方法主要有偽譜法[1-2]、有限元法[3-4]、有限差分法[5-9]等。其中有限差分法具有內存占用小、易于實現和計算效率高的優點，因此它在波動方程數值模擬領域中廣受歡迎。但是由于差分網格離散引起的數值頻散無法避免，直接影響數值模擬的精度。

時域有限差分方法求解波動方程在時間域和空間域同時進行，按照數值相速度和真實傳播速度的相對大小，其固有的頻散誤差可分為時間頻散和空間頻散[10]。Koene等[11]提出的時間頻散變換，在遠遠超過穩定性極限所允許的時間步長條件下，能很好地去除時間頻散。因此，本文主要針對空間頻散問題開展研究。通常用于壓制空間數值頻散的方法有以下幾種：其一，采用較小的空間步長[12]，但這會大大增加計算量和所需計算內存；其二，空間方向采用高階差分格式[13]；其三，利用FCT(Flux-Corrected Transport)技術[14-15]削弱數值頻散影響；其四，利用優化算法求取新的差分系數[16-20]進行波動方程數值模擬。在相同階數下，相對于傳統泰勒級數展開(TE)方法，利用優化算法求取新的差分系數在較大波數域區間精度更高，因此能取得更好的數值頻散壓制效果。Holberg[16]首次提出通過最小化給定空間頻帶內群速度的峰值相對誤差優化空間有限差分(FD)算子，但是對群速度的最大相對誤差沒有嚴格的限制，導致模擬結果與精確解有較大偏差。Liu[17]基于L2范數建立目標函數，采用最小二乘法(LS)優化近似求取差分系數。此外，Zhang等[18]、Yang等[19]、He等[20]基于L∞范數建立目標函數求解有限差分系數，用于波動方程數值模擬。Zhang等[18]用模擬退火算法求得了聲波方程空間導數的有限差分系數，并且給出了0.0001的誤差容限。Yang等[19]采用Remez迭代算法求解空間一階偏導數交錯網格差分系數。He等[20]在Yang等[19]的基礎上引入新的約束條件，得到“等波紋”解，獲得理論上最寬有效頻帶。

現有的L2范數和L∞范數方法只考慮峰值誤差，缺乏對中低波數的誤差約束，因此實際數值測試中的誤差積累較大。雖然上述方法都能有效減少數值頻散，但是應該更加關注有限差分方法在波場傳播中的誤差積累，而不是一味地追求給定誤差容限下的最大覆蓋帶寬[20-21]。Miao等[21]基于L1范數建立新的目標函數，然后通過交替方向乘子法算法(ADMM)[22]獲得了空間二階偏導數的規則網格有限差分系數。數值實驗表明，在不改變誤差容限的情況下，此方法盡管略微降低了有效帶寬的覆蓋范圍，但是能加強對中低波數的誤差約束，減小有效帶寬內的總誤差。

本文首先將ADMM優化方法推廣到空間一階偏導數交錯網格有限差分系數的求解，將其用于一階應力—速度聲波方程的交錯網格有限差分數值模擬。然后對基于三種不同范數優化方法進行頻散曲線誤差分析。最后利用均勻介質模型和復雜模型的長時程數值實驗，證明本文L1范數優化方法在減小誤差積累方面的優越性。

1 方法原理

1.1 交錯網格有限差分格式

非均勻介質的二維一階應力—速度聲波方程組可表示為

(1)

式中：P為應力(標量)；Vx和Vz分別表示x和z方向上質點振動速度分量；ρ為介質密度；v為地震波速度。

交錯網格有限差分格式在同等條件下比規則網格有限差分格式精度更高。通常，使用高階有限差分系數可以提高空間導數的精度[7]，空間一階導數的2M階有限差分交錯網格定義為

(2)

式中：cm是有限差分系數；h是空間網格間距。根據平面波理論有

u(x)=u0ejkx

(3)

式中：u0是常數；j為虛數單位；k為波數。令β=kh/2，代入式(2)得到

(4)

本文的目的是通過在給定范圍內最小化絕對誤差的總和計算優化的差分系數。絕對誤差的總和可以表示為

(5)

將上式中β離散為β(i)=ikmaxh/N,其中N為離散度，kmax為最大波數。在忽略常數項kmaxh/N后，目標函數E可寫成

(6)

1.2 目標函數的重構和正則化

將式(6)改寫成線性方程組的形式

(7)

(8)

Wang等[23]證明了直接優化目標函數F(c)的常系數矩陣c可能導致數值振蕩。因此，使用正則化技術[24]克服不穩定解。建立正則化目標函數為

ψ(c)=F(c)+J(c)

(9)

(10)

式中：α=0.0001為正則化參數；D為單位矩陣。本文的目的是通過求解正則化的問題來找到最優解，即

(11)

1.3 求解正則化最小模型

式(11)為非線性問題，目前可以運用多種方法求解。但是為了高效和精確地求得常系數，采用交替方向乘子法[22]將原始問題轉換為約束問題

(12)

式中d=Ac+b，對應的增廣拉格朗日函數可以寫成

(13)

式中：u為拉格朗日變量；η為軟閾值。后面的模型測試中取η=40。

ADMM求解最小化模型主要分為三步：更新c、更新d、更新u。

第一步：更新c

(14)

(15)

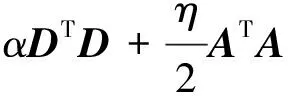
第二步：更新d

(16)

上式為一個套索問題[26]，可以用次微分學的封閉形式解決。上式的解可以表達成

d(k+1)=S1/η(Ac(k+1)+b+u(k))

(17)

式中軟閾值算子S定義為

(18)

第三步：更新u

u(k+1)=u(k)+(Ac(k+1)+b-d(k+1))

(19)

1.4 搜索有限頻帶范圍的最大值kmax

為了得到帶寬的上限kmax，本文計算不同kmax和M條件下的最大誤差

(20)

(21)

為了尋找最優解，從一個小的kmax開始，它產生一個最大誤差εmax。當εmax小于給定的容錯允差時，稍微增大kmax并重復上述過程，直到εmax等于(或小于)給定的容錯允差。表1為M=8時不同范數優化后求解的差分系數。L1范數優化后求解的差分系數如表2所示。

表1 不同優化方法的差分系數(M=8)

表2 一階導數交錯網格有限差分系數

從圖1中不同差分階數的頻散曲線可以看出，采用增大差分階數可以獲得更廣的頻帶覆蓋范圍，且隨著差分階數的增加，低波數區間的頻散誤差逐漸減小。為了對各種方法進行比較，分別基于L1范數、L2范數[12]和L∞范數[20]求解聲波方程的交錯網格有限差分系數，并對其進行頻散分析。圖2中，在M=8(16階)時，在誤差閥值為0.0001的條件下，相對于L2范數和L∞范數來說，盡管基于L1范數優化方法頻帶覆蓋范圍略微變窄，但能更好地約束在中低波數區間的頻散誤差。

圖1 L1范數優化后的頻散曲線

圖2 三種范數約束下的頻散曲線(M=8)

1.5 穩定性分析

二維一階應力—速度聲波方程交錯網格有限差

分離散格式的穩定性條件[26]為

r≤s

(22)

式中：r為庫郎數；s為穩定性因子[27]

(23)

泰勒展開與L1、L2、L∞約束下的穩定性因子曲線如圖3所示。

圖3 不同方法的穩定性因子隨差分階數(2M)的變化

總體來看，無論是傳統TE方法還是各種范數的優化方法，穩定性因子s都會隨著差分階數的增大而減小。此外，在相同差分階數時，TE方法穩定性因子的值大于其他優化方法。值得注意的是，本文利用L1范數約束優化求得差分系數的穩定性因子比另外兩種范數大，證明其穩定性限制條件比另外兩種方法寬松。

2 理論模型試算

在本次正演模擬實驗中，分別對均勻介質模型和Marmousi Ⅱ模型進行正演數值模擬。

2.1 均勻介質模型

均勻介質模型中，縱波速度為2000m/s，網格大小為401×401，網格間距h=5m，時間步長為0.2ms，使用主頻為30Hz的雷克子波，震源放在模型的中心位置(1005m，1005m)。為獲得聲波長時長的傳播記錄，在未加邊界條件下，總采樣時間設為2s。不同優化方法得到二維交錯網格有限差分聲波方程數值模擬的波場快照如圖4所示；圖5為基于三種不同范數優化方法與采用傳統泰勒120階展開算法的模擬結果(參考解)的差值。在接收點Ra(1500m，500m)和Rb(1000m，500m)的單點部分接收記錄如圖6所示；圖7為基于三種不同范數優化方法結果與參考解的差值。

圖4 均勻介質模型波場快照(左圖：t=0.5s；右圖t=2.0s)

圖5 均勻介質模型波場快照與參考解的差值(左圖：t=0.5s；右圖t=2.0s)

圖6 均勻介質模型Ra和Rb單點部分時段接收記錄

圖7 均勻介質模型Ra和Rb單點部分接收時段記錄與參考解的差值

從圖5中波場快照的差值對比可看出，三種不同范數優化算法的模擬結果中，對誤差控制最好的為L1范數，其次是L2范數，最差的是L∞范數，這與頻散關系(圖2)分析結果是一致的。圖5中t=2.0s時刻的差值比t=0.5s時刻更大，說明隨著波場傳播時間的增加，誤差積累更嚴重。L1范數對誤差積累的控制較好，從Ra點和Rb點接收記錄分析(圖6、圖7)也可得出這一結論。

2.2 復雜模型

復雜模型Marmousi Ⅱ速度模型如圖8所示，縱波速度范圍為1500m/s～4800m/s。震源函數使用主頻為25Hz的雷克子波，震源在(1800m，250m)處，接收線與炮點同深度且水平排列。空間步長5m，時間采樣間隔0.2ms，總采樣時長4s。用不同優化方法得到二維交錯網格有限差分聲波方程數值模擬的單炮記錄，提取第200道和第500道的部分時段地震記錄如圖9所示，圖10為基于三種不同范數優化方法模擬結果與參考解的差值。不同優化方法得到的單炮炮集如圖11所示，與參考解的炮集差如圖12所示。

圖8 MarmousiⅡ模型(網格681×561)

圖9 MarmousiⅡ模型第200道(上)和第500道(下)部分時段地震記錄

圖10 MarmousiⅡ模型第200道(上)和第500道(下)部分時段地震記錄與參考解的差值

圖11 不同方法模擬的MarmousiⅡ模型單炮炮集

在第200道和第500道的地震記錄上(圖9)，從波形上看，三種范數都與參考解比較吻合。但從單道誤差(圖10)分析來看，L1范數對誤差積累的控制效果更好；從炮集誤差對比(圖12)可得出，L1范數對誤差積累的控制效果最好，特別是對深層目標模擬誤差控制更為明顯。

圖12 不同方法模擬的MarmousiⅡ模型單炮炮集與參考解(泰勒120階模擬)炮集的差值

3 結論

本文基于L1范數建立了求取空間域一階偏導交錯網格有限差分系數的目標函數，采用ADMM算法計算了差分系數，進行了一階應力—速度聲波方程的均勻介質模型和復雜模型的正演模擬。主要結論如下：

(1)建立了空間一階偏導數交錯網格有限差分系數基于L1范數的目標函數，并通過ADMM算法求解，與L2范數、L∞范數優化后的差分系數頻散關系進行了對比，在0.0001容許誤差條件下，L1范數以犧牲很小的頻帶覆蓋范圍使較小波數范圍的誤差得到更好的控制；

(2)通過對均勻介質模型和復雜模型的數值模擬得知，在對深層目標進行數值模擬時，隨著波場的延拓，誤差積累現象會更加嚴重，這時對誤差的控制就顯得尤為重要。本文基于L1范數建立的目標函數優化差分系數，更有利于降低在對深層目標的數值模擬中的誤差積累。