特高壓換流變壓器拉板損耗的頻率特性分析
黃天超 王澤忠
(華北電力大學(xué)高電壓與電磁兼容北京市重點(diǎn)實(shí)驗(yàn)室 北京 102206)
0 引言
隨著高壓直流輸電系統(tǒng)容量的不斷提升,換流變壓器的安全穩(wěn)定運(yùn)行就顯得十分重要。不同于交流變壓器,換流變壓器正常工作時(shí)繞組中將有高次諧波電流流過(guò),因此其負(fù)載損耗的計(jì)算將更加復(fù)雜[1]。其中安裝于鐵心主柱疊片最外層起到承重作用的拉板,其表面漏磁將遠(yuǎn)大于油箱、夾件等結(jié)構(gòu)件,因此雖然拉板損耗占總的負(fù)載損耗比例并不大,但由于高入射磁通密度和較差的冷卻條件,局部溫升會(huì)非常高[2]。如果不能精確地計(jì)算換流變壓器負(fù)載電流中各次諧波電流造成的拉板損耗,就可能導(dǎo)致對(duì)熱點(diǎn)溫升的低估,進(jìn)而引起拉板附近的絕緣材料老化[3],嚴(yán)重影響換流變壓器的壽命和使用。
目前針對(duì)變壓器拉板損耗的最新研究比較少。文獻(xiàn)[4]假設(shè)低壓繞組內(nèi)表面的磁場(chǎng)強(qiáng)度沿著拉板高度的方向在空間中呈周期性正弦變化,結(jié)合試驗(yàn)數(shù)據(jù)給出了拉板損耗的解析公式。為了更加精確地計(jì)算拉板損耗并對(duì)拉板開(kāi)槽的影響進(jìn)行分析,文獻(xiàn)[5]運(yùn)用2D/3D有限元法,量化了不同因素對(duì)拉板損耗的影響,并對(duì)不同材料、不同開(kāi)槽的數(shù)量、寬度下渦流的路徑進(jìn)行了深入的分析。文獻(xiàn)[6]則在文獻(xiàn)[5]的基礎(chǔ)上以降低拉板損耗為目的,對(duì)拉板的結(jié)構(gòu)進(jìn)行了優(yōu)化設(shè)計(jì)。文獻(xiàn)[7]針對(duì)換流變壓器拉板開(kāi)槽的特殊性,分析了拉板開(kāi)全槽和半槽對(duì)其損耗計(jì)算結(jié)果的影響。然而上述研究都是針對(duì)拉板基波損耗,沒(méi)有考慮換流變壓器中高次諧波電流對(duì)拉板損耗的影響。
換流變壓器額定負(fù)載電流中含有大量諧波成分,如果知道損耗與電流頻率的關(guān)系,就可以依據(jù)基波損耗快速計(jì)算出總的諧波損耗。文獻(xiàn)[8-11]最早提及換流變壓器損耗頻率特性,通過(guò)實(shí)測(cè)數(shù)據(jù)的分析,其分別認(rèn)為換流變壓器結(jié)構(gòu)件損耗的頻率指數(shù)為0.9、1、1.4和1.5。2017年,IEEE—60076—57—129標(biāo)準(zhǔn)中制定了HVDC換流變壓器負(fù)載損耗的計(jì)算方法,該標(biāo)準(zhǔn)假設(shè)換流變壓器中結(jié)構(gòu)件雜散損耗與電流的二次方成正比,與頻率的0.8次方成正比。文獻(xiàn)[12]則基于Problem21系列基準(zhǔn)模型,以實(shí)驗(yàn)的形式分別研究了換流變壓器油箱、夾件、拉板等結(jié)構(gòu)件各自的諧波損耗頻率特性,文獻(xiàn)[12]認(rèn)為拉板損耗的頻率指數(shù)為1.5。文獻(xiàn)[13]對(duì)比研究了諧波電流對(duì)導(dǎo)磁和非導(dǎo)磁結(jié)構(gòu)件雜散損耗的影響。但上述研究不是沒(méi)有專門(mén)針對(duì)拉板損耗進(jìn)行研究,就是沒(méi)有理論依據(jù)。
因此本文結(jié)合拉板表面磁場(chǎng)分布的特點(diǎn),簡(jiǎn)化磁場(chǎng)方程,推導(dǎo)了拉板損耗的計(jì)算公式。通過(guò)公式分析,得到不同拉板開(kāi)槽情況下,其損耗頻率指數(shù)變化規(guī)律和范圍大小。為了驗(yàn)證理論分析的正確性并進(jìn)一步確定實(shí)際拉板損耗計(jì)算的頻率指數(shù)數(shù)值,針對(duì)一臺(tái)800kV特高壓換流變壓器拉板損耗進(jìn)行了有限元仿真計(jì)算。結(jié)果表明,拉板開(kāi)槽在減小基波損耗的同時(shí)還會(huì)增加高次諧波損耗,導(dǎo)致其損耗頻率指數(shù)的大幅增加。實(shí)際計(jì)算中可取數(shù)值1.5,遠(yuǎn)大于不開(kāi)槽時(shí)的數(shù)值0.6。該結(jié)論可為快速準(zhǔn)確地計(jì)算換流變壓器負(fù)載情況下拉板損耗提供理論依據(jù)。
1 拉板渦流損耗模型
換流變壓器拉板安裝在鐵心主柱疊片最外層,面向網(wǎng)側(cè)繞組的內(nèi)表面。漏磁通從網(wǎng)側(cè)繞組端部徑向離開(kāi),近似垂直地射入拉板中,因此拉板的渦流損耗主要集中在與繞組端部平齊的位置,且沿著拉板寬度方向的中心軸左右對(duì)稱分布。換流變壓器拉板為不銹鋼材料,磁導(dǎo)率遠(yuǎn)小于鐵心硅鋼片,再加上其厚度很薄,所以可以假設(shè)磁場(chǎng)垂直穿透拉板進(jìn)入鐵心。基于實(shí)驗(yàn)數(shù)據(jù),拉板表面的磁場(chǎng)強(qiáng)度沿著它的長(zhǎng)度方向在空間中呈正弦變化[4],在磁場(chǎng)最大值附近可認(rèn)為其為二次函數(shù)分布。圖1為簡(jiǎn)化的拉板渦流損耗分析模型,x、y、z分別為拉板厚度、長(zhǎng)度、寬度方向,b為拉板寬度數(shù)值的一半。
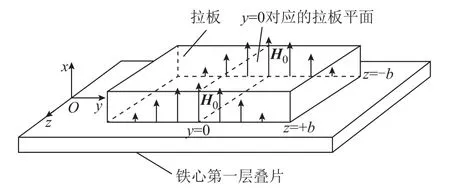
圖1 拉板渦流損耗分析模型Fig.1 Eddy current loss analysis model of flitch plate
準(zhǔn)靜態(tài)電磁場(chǎng)方程為
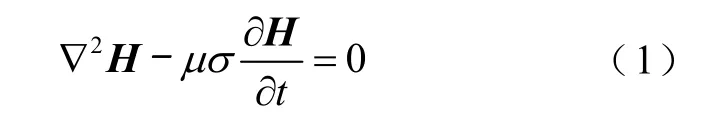
式中,μ、σ分別為拉板的磁導(dǎo)率和電導(dǎo)率,均為常數(shù);H為磁場(chǎng)強(qiáng)度的向量形式。假設(shè)正弦變化的拉板表面磁場(chǎng)強(qiáng)度H只有x方向,且僅為y、z方向的函數(shù)。式(1)可化簡(jiǎn)為

式中,j為虛數(shù)單位;ω為角頻率。因?yàn)閤方向磁場(chǎng)強(qiáng)度Hx沿著y軸長(zhǎng)度方向呈二次函數(shù)分布,所以其二階導(dǎo)數(shù)為常數(shù),假設(shè)Hx對(duì)y的二階導(dǎo)數(shù)在z方向隨著磁場(chǎng)強(qiáng)度Hx線性變化。磁場(chǎng)強(qiáng)度在y方向最大值位置(低壓繞組端部水平對(duì)應(yīng)的拉板左右兩側(cè),y= 0,z=±b)的峰值為H0。此時(shí)式(2)可進(jìn)一步化簡(jiǎn)為
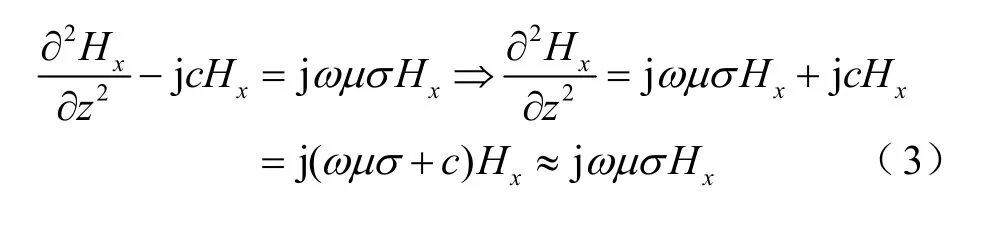
式中,c為正常數(shù),由于拉板的長(zhǎng)度遠(yuǎn)大于趨膚深度,因此在數(shù)值上,ωμσc,即忽略磁場(chǎng)強(qiáng)度Hx在y方向變化的影響。此時(shí)方程變成一元二階微分方程,形式上與繞組的渦流損耗方程一致[14-15]。結(jié)合邊界條件:y=0,z=±b時(shí)Hx=H0,可解得Hx為
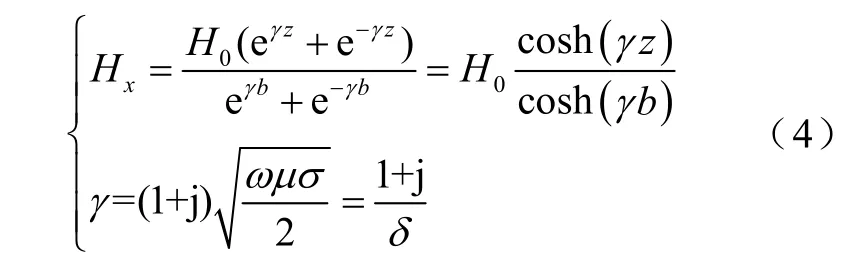
式中,δ為趨膚深度,。
因?yàn)樵趛方向上Hx呈正弦變化,變化率很小且與頻率無(wú)關(guān),因此拉板的總損耗頻率特性和y=0對(duì)應(yīng)的拉板平面的損耗頻率特性一致。所以只需分析計(jì)算y=0拉板平面單位厚度上的損耗Ps即可。

將式(6)代入到式(5),化簡(jiǎn)可得
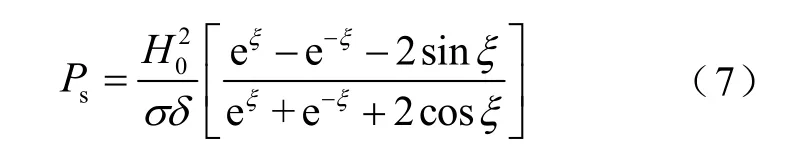
式中,ξ為歸一化拉板寬度,ξ= 2bδ。
2 拉板損耗頻率特性理論分析
IEEE標(biāo)準(zhǔn)中推薦使用式(8)計(jì)算換流變壓器結(jié)構(gòu)件損耗。
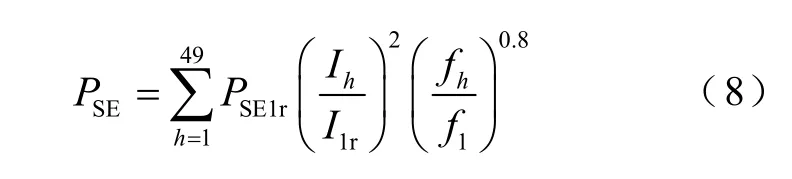
式中,PSE為結(jié)構(gòu)件損耗;PSE1r為基頻測(cè)量損耗;I1r為基頻測(cè)試電流;f1為基波頻率;h為諧波次數(shù)。Ih、fh分別為對(duì)應(yīng)諧波的電流和頻率。使用該公式可以快速計(jì)算任意負(fù)載電流頻譜下的換流變壓器結(jié)構(gòu)件損耗。對(duì)于拉板損耗而言,由于磁場(chǎng)強(qiáng)度與電流數(shù)值成正比,由式(7)可知拉板損耗電流指數(shù)為2,這與式(8)中給出的數(shù)值一致。但該公式中給出的損耗頻率指數(shù)為0.8,是綜合考慮了換流變壓器中各個(gè)結(jié)構(gòu)件得到的。因此該頻率指數(shù)是否適用于拉板損耗是值得分析的。
當(dāng)2bδ時(shí),ξ1,式(7)可化簡(jiǎn)為
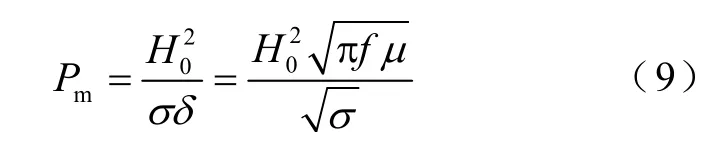
式中,Pm為拉板寬度遠(yuǎn)大于趨膚深度時(shí)的損耗值。將拉板損耗Ps歸算到Pm,可得歸一化后的拉板損耗曲線如圖2所示。
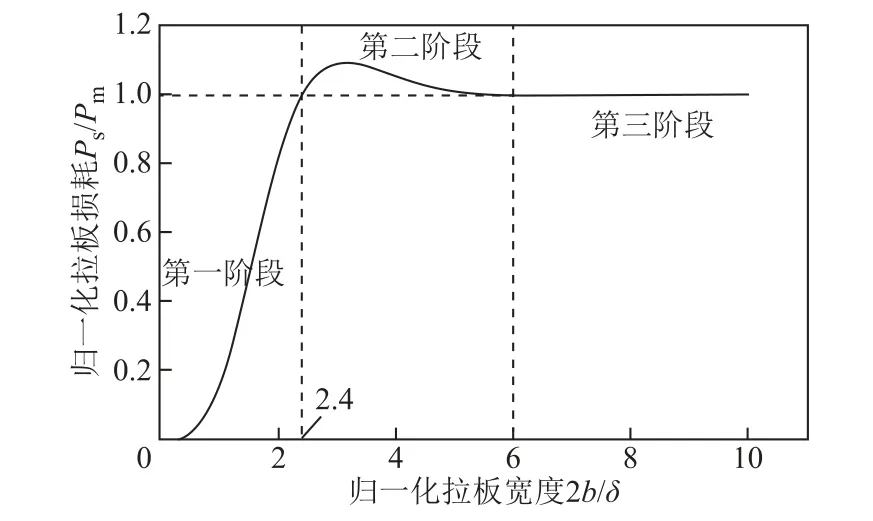
圖2 拉板渦流損耗與寬度關(guān)系圖Fig.2 Relation diagram of eddy current loss and width of flitch plate
由圖2可知,拉板的損耗和拉板歸一化寬度之間的變化趨勢(shì)可分為三個(gè)階段。在第一階段,即歸一化拉板寬度ξ<2.4時(shí),拉板損耗隨著拉板歸一化寬度的增加急劇增大;之后進(jìn)入一個(gè)短暫的漸穩(wěn)狀態(tài),即第二階段;當(dāng)其數(shù)值達(dá)到臨界值6時(shí),拉板損耗基本維持在一個(gè)恒定值Pm,進(jìn)入穩(wěn)定的第三階段。換流變壓器的拉板寬度大約在300~400mm之間,其材料為不銹鋼。50Hz時(shí)趨膚深度為67mm,對(duì)應(yīng)的歸一化拉板寬度范圍約為4.5~6。因此當(dāng)拉板不開(kāi)槽時(shí)各個(gè)諧波頻率下,拉板損耗可直接由式(9)計(jì)算,此時(shí)拉板的損耗頻率指數(shù)取值為0.5。
為了降低拉板損耗,實(shí)際換流變壓器拉板會(huì)開(kāi)槽,且為全槽。假設(shè)開(kāi)槽數(shù)為n,此時(shí)拉板的總損耗為n+1個(gè)寬度約為原來(lái)1(n+1)的小拉板組成。由圖2可知,電流頻率為基波50Hz時(shí),由于小拉板寬度的大幅減小導(dǎo)致其損耗關(guān)系曲線進(jìn)入到第一階段,造成損耗數(shù)值的急劇減小,使得最終n+1個(gè)小拉板相加損耗仍然小于不開(kāi)槽時(shí)的數(shù)值。但是對(duì)于高頻的諧波而言,其趨膚深度遠(yuǎn)小于基波時(shí)的數(shù)值,因此拉板開(kāi)槽并不會(huì)導(dǎo)致每個(gè)小拉板的歸一化拉板寬度小于臨界數(shù)值6,其損耗曲線一直穩(wěn)定在第三階段,造成總的損耗的增加。因此換流變壓器拉板開(kāi)槽時(shí)基波損耗會(huì)減小,但隨著電流頻率的增加該效果會(huì)越來(lái)越弱,當(dāng)頻率達(dá)到一定數(shù)值時(shí)損耗不降反升。當(dāng)頻率足夠大時(shí),開(kāi)槽后每個(gè)小拉板的損耗等于沒(méi)開(kāi)槽時(shí)整個(gè)拉板的損耗,所以開(kāi)槽后的拉板總損耗將會(huì)是不開(kāi)槽時(shí)的n+1倍。因此對(duì)于實(shí)際拉板開(kāi)槽的換流變壓器而言,其拉板的諧波損耗與基波損耗換算的損耗頻率指數(shù)將遠(yuǎn)大于不開(kāi)槽時(shí)的理論數(shù)值0.5。
3 有限元模型
3.1 換流變壓器拉板有限元模型的搭建
為了驗(yàn)證理論分析的正確性,運(yùn)用有限元仿真軟件COMSOL,針對(duì)一臺(tái)800kV換流變壓器的鐵心主柱拉板損耗進(jìn)行了仿真計(jì)算。該換流變壓器為單相四柱式結(jié)構(gòu),套在中間兩主柱上的對(duì)應(yīng)繞組之間并聯(lián)連接,網(wǎng)側(cè)繞組在內(nèi),閥側(cè)繞組在外,兩者的電流流向相反。鐵心主柱上的拉板均勻開(kāi)兩槽,與交流變壓器開(kāi)半槽不同的是,換流變壓器拉板為全槽。具體尺寸:拉板寬度為400mm,長(zhǎng)度為3 600mm,厚度為25mm,開(kāi)槽寬度為10mm;鐵心長(zhǎng)6.58m,寬1.132m,高3.92m;鐵心主柱截面積為1.17m2。換流變壓器額定參數(shù)和材料參數(shù)見(jiàn)表1和表2。上述數(shù)據(jù)均為生產(chǎn)廠家提供。
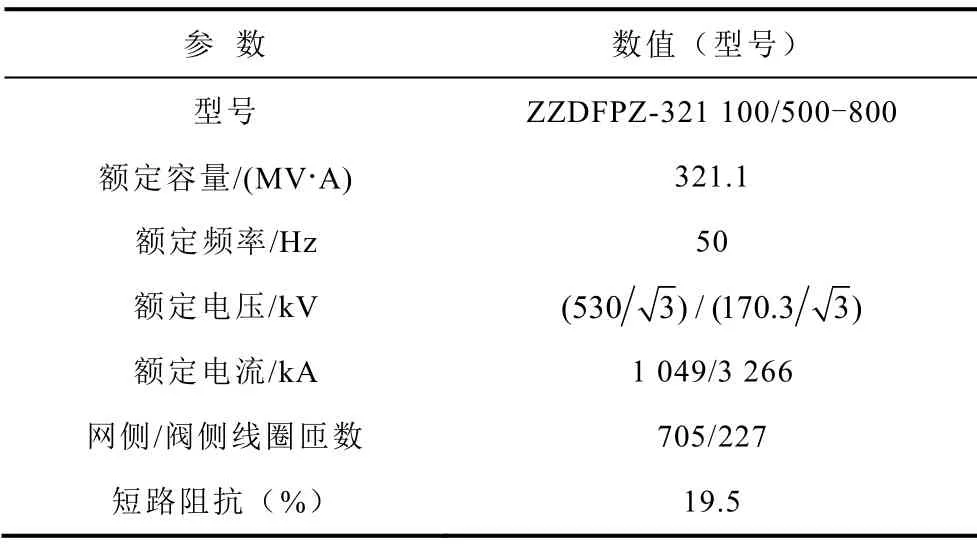
表1 換流變壓器參數(shù)Tab.1 Converter transformer parameters

表2 材料參數(shù)Tab.2 material parameter
圖3為換流變壓器八分之一有限元模型。在建模過(guò)程中進(jìn)行了以下簡(jiǎn)化和考慮:①對(duì)鐵心進(jìn)行整體建模,不考慮鐵心疊片結(jié)構(gòu);②忽略鐵心和繞組的渦流損耗;③對(duì)拉板進(jìn)行充分的網(wǎng)格剖分,尤其是在拉板寬度的左右兩側(cè),保證在一個(gè)趨膚深度內(nèi)至少有五個(gè)單元;④由于換流變壓器具有對(duì)稱結(jié)構(gòu),為了減小計(jì)算量,只構(gòu)建其八分之一模型,對(duì)應(yīng)的邊界條件為:XZ平面和YZ平面設(shè)置為磁力線垂直邊界條件,其余四個(gè)外邊界設(shè)置為磁力線平行邊界條件;⑤模型激勵(lì)為直接在網(wǎng)側(cè)和閥側(cè)繞組橫截面施加方向相反的電流激勵(lì)。
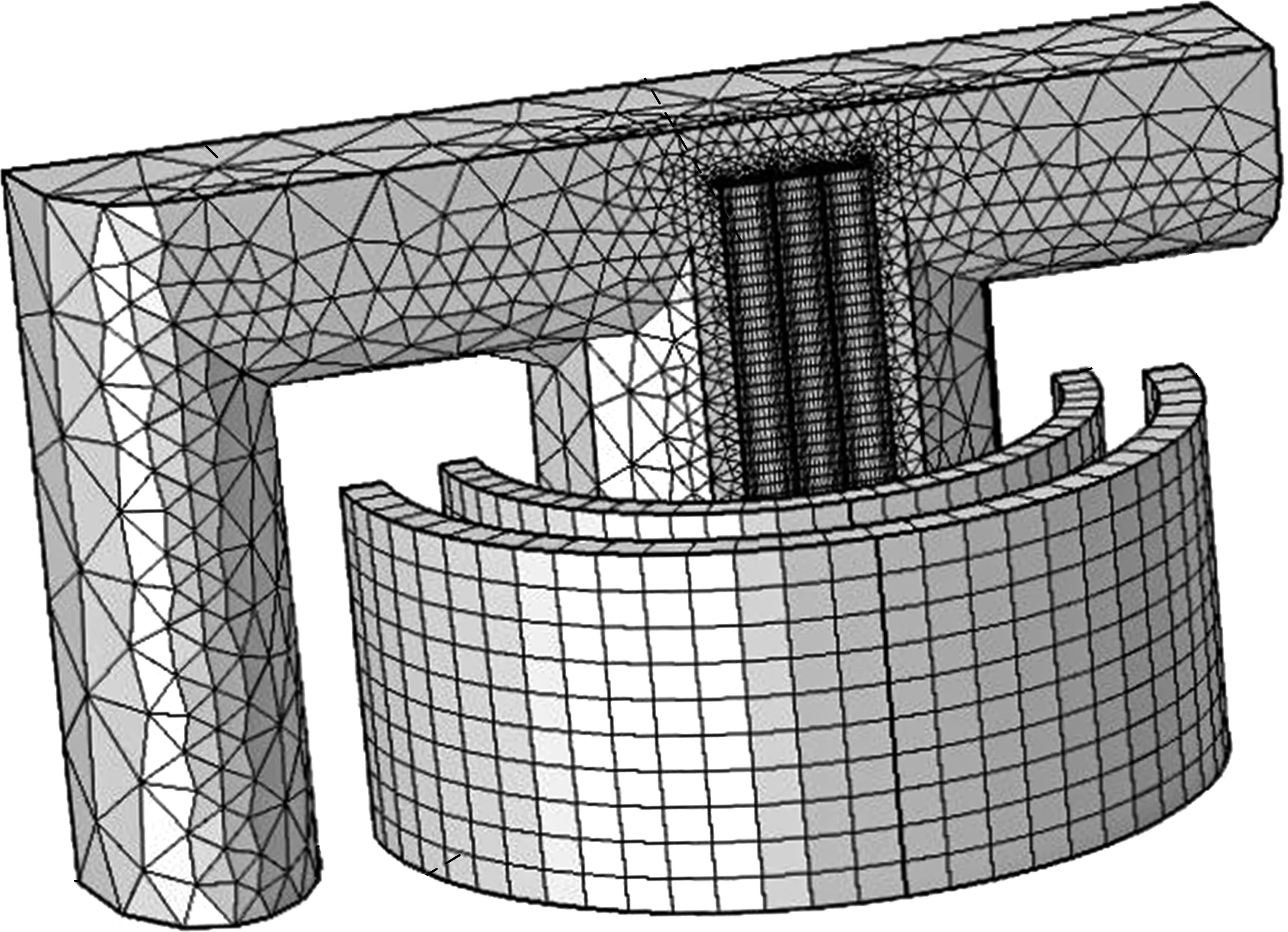
圖3 換流變壓器八分之一有限元模型Fig.3 One-eighth finite element model of converter transformer
3.2 Problem21a模型的驗(yàn)證
由于無(wú)法將換流變壓器拉板損耗從測(cè)量的總損耗中分離出來(lái),因此不能通過(guò)實(shí)驗(yàn)的形式直接驗(yàn)證3.1節(jié)有限元模型的正確性。TEAM Problem 21基準(zhǔn)族是為了解決變壓器結(jié)構(gòu)件損耗計(jì)算而提出的一系列標(biāo)準(zhǔn)模型,其中Problem21a-2模型是以變壓器鐵心拉板開(kāi)兩槽為背景。因此可以通過(guò)使用3.1節(jié)的建模方式搭建Problem21a-2模型,再將仿真得到的數(shù)值與標(biāo)準(zhǔn)模型提供的實(shí)測(cè)數(shù)據(jù)進(jìn)行比較,以此來(lái)間接地驗(yàn)證3.1模型的正確性。圖4為Problem21a-2模型詳細(xì)結(jié)構(gòu)尺寸。圖5為其四分之一有限元模型。文中模型的尺寸數(shù)據(jù)與實(shí)測(cè)的各種數(shù)值來(lái)源于最新版本的TEAM Problem 21 Family(V.2 009)。
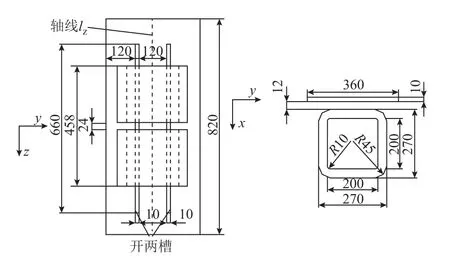
圖4 Problem21a-2模型結(jié)構(gòu)尺寸Fig.4 Problem21a-2 model structural dimensions
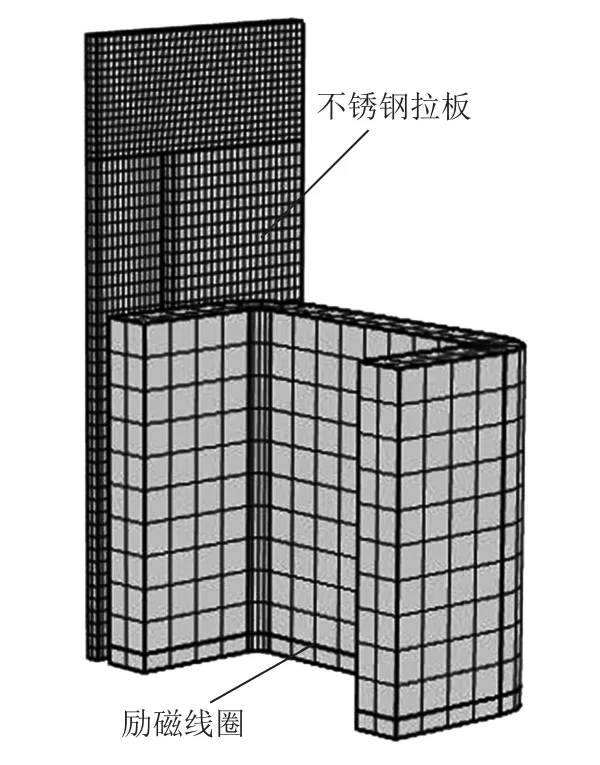
圖5 Problem21a-2四分之一有限元模型Fig.5 Quarter finite element model of Problem21a-2
繞組中施加的電流有效值為10A,頻率為50Hz。拉板的材料為不銹鋼,繞組為銅。仿真得到的拉板損耗數(shù)值為1.69W,而實(shí)測(cè)數(shù)值為1.68W,兩者的誤差僅有0.6%。表3為Problem21a-2模型中沿拉板表面軸線lz分布的徑向磁通密度Bx的仿真值和測(cè)量值。
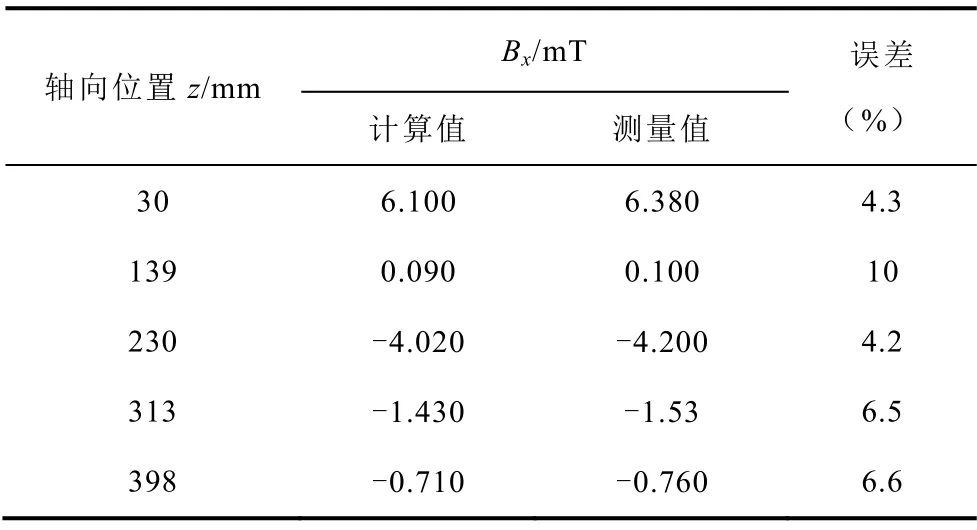
表3 Problem21a-2拉板表面磁感應(yīng)強(qiáng)度BxTab.3 Flitch plate surface Bx of Problem21a-2
通過(guò)表3和拉板損耗數(shù)值的對(duì)比可以看出,仿真與實(shí)測(cè)數(shù)值之間誤差很小。因此3.1小節(jié)建立的換流變壓器拉板有限元模型是正確的。
4 仿真分析
圖6為本文所使用的換流變壓器閥側(cè)額定負(fù)載電流頻譜圖。從圖6中可以看出,諧波含量隨著頻率的增加呈指數(shù)下降,而拉板損耗與電流數(shù)值的二次方成正比,所以高頻諧波造成的損耗與基波損耗相比很小。又因?yàn)槠渲C波含量主要由6n±1次諧波組成,n為正整數(shù)[17-18],相鄰兩次諧波頻率相差很小。因此仿真只計(jì)算了電流頻率為50Hz、250Hz、550Hz、850Hz和2 450Hz下拉板不開(kāi)槽和開(kāi)兩全槽時(shí)的損耗。由于該換流變壓器采用的是兩主柱上繞組并聯(lián)連接的方式,因此3.1節(jié)有限元模型中繞組中通入的電流為額定電流的一半。
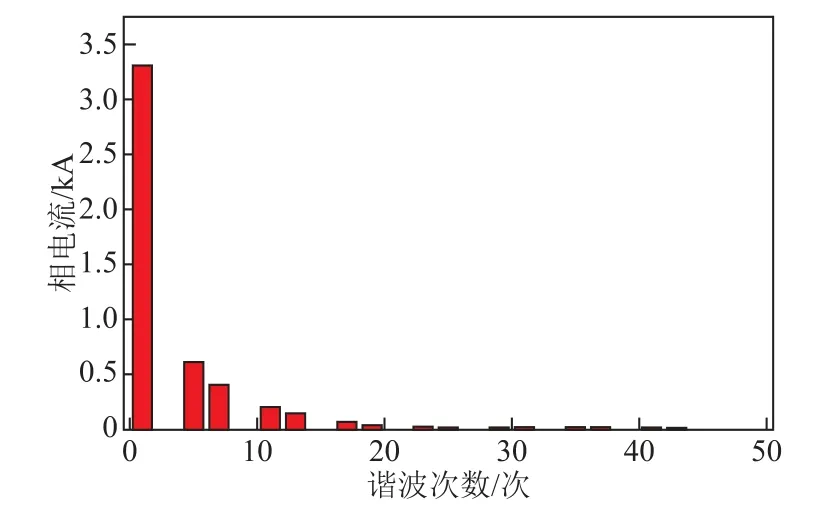
圖6 換流變壓器額定負(fù)載電流頻譜Fig.6 Rated load current spectrum of converter transformer
4.1 拉板表面渦流和磁場(chǎng)分布結(jié)果分析
圖7a、圖7b分別為拉板不開(kāi)槽和開(kāi)兩全槽時(shí),電流頻率50Hz下拉板正表面和側(cè)表面的渦流密度分布局部圖,圖中拉板側(cè)表面與正表面的長(zhǎng)度尺寸關(guān)系為虛線框所示。從圖7a中可以看出拉板不開(kāi)槽時(shí),渦流基本沿著拉板的長(zhǎng)度方向(y軸方向)流動(dòng),且在厚度方向(x軸方向)上渦流密度均勻分布。在寬度方向(z軸方向)上,渦流沿著拉板中心軸左右對(duì)稱分布,主要集中在拉板的兩側(cè),且渦流損耗最大值位置與繞組端部等高。這與文獻(xiàn)[5]中圖6a和圖6c得到的渦流密度分布圖基本一致。對(duì)比圖7b可以發(fā)現(xiàn),拉板開(kāi)全槽并不會(huì)改變渦流在每一個(gè)小拉板上的流向。
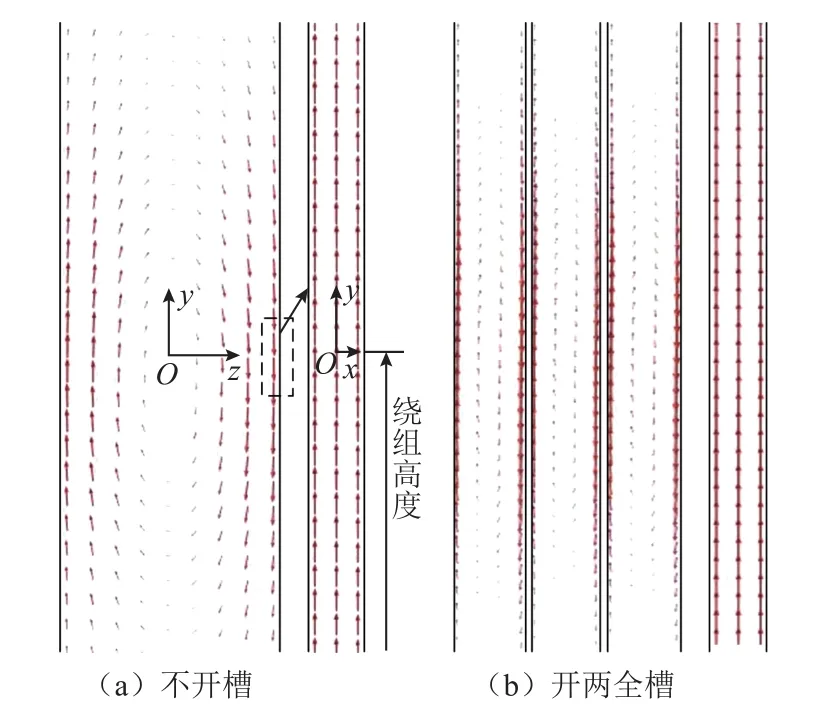
圖7 拉板表面渦流分布Fig.7 Eddy current distribution on flitch plate surface
圖8a、圖8b分別為拉板不開(kāi)槽和開(kāi)兩全槽時(shí),基波電流和17次諧波電流下拉板正表面x軸方向磁場(chǎng)強(qiáng)度Hx分布圖。從圖8a可以清楚地看到,隨著電流頻率的增加,磁場(chǎng)強(qiáng)度的趨膚現(xiàn)象越來(lái)越明顯。當(dāng)電流頻率為850Hz即17次諧波時(shí),可以認(rèn)為拉板在寬度方向上除了兩側(cè)表面,內(nèi)部沒(méi)有磁場(chǎng)強(qiáng)度分布。由于拉板沒(méi)有開(kāi)槽,其寬度遠(yuǎn)大于基波趨膚深度,因此基波磁場(chǎng)強(qiáng)度仍只存在拉板兩側(cè),拉板中部并沒(méi)有磁場(chǎng)強(qiáng)度分布。當(dāng)拉板開(kāi)槽時(shí),由圖8b可知,磁場(chǎng)強(qiáng)度在每一個(gè)小拉板上的分布情況除數(shù)值大小外其余完全一樣。電流頻率為基頻時(shí),磁場(chǎng)強(qiáng)度在每一個(gè)小拉板正表面上與不開(kāi)槽時(shí)相比分布得很均勻。但是對(duì)于17次諧波而言,拉板開(kāi)槽后每個(gè)小拉板的寬度仍遠(yuǎn)大于其趨膚深度,因此磁場(chǎng)強(qiáng)度分布規(guī)律與不開(kāi)槽時(shí)相同,都是在拉板的兩側(cè),拉板中部并沒(méi)有磁場(chǎng)強(qiáng)度分布。
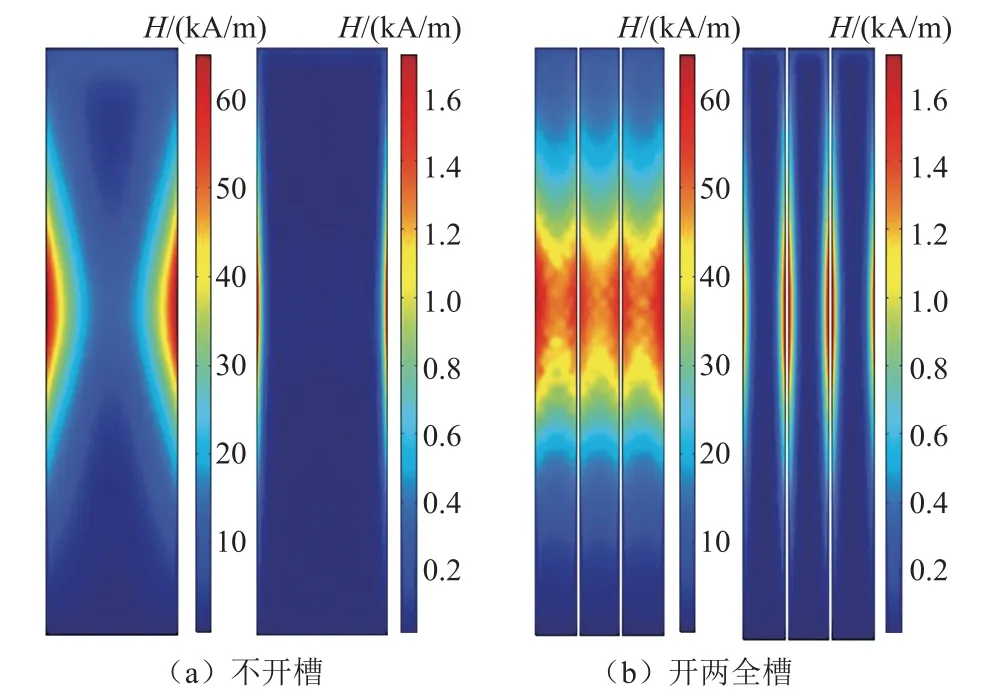
圖8 拉板表面磁場(chǎng)Hx分布Fig.8 Magnetic fieldHxon flitch plate surface
綜上所述,拉板表面渦流和磁場(chǎng)強(qiáng)度分布的計(jì)算結(jié)果與第1、2節(jié)理論分析的結(jié)論一致,這也證明了本文所建立的有限元仿真模型的正確性。
4.2 拉板損耗頻率特性分析
為了方便分析電流頻率對(duì)拉板損耗的影響規(guī)律,并確定頻率指數(shù),假設(shè)諧波電流在數(shù)值上與基波一樣,因?yàn)槔鍝p耗與電流的二次平方成正比,此時(shí)對(duì)應(yīng)的諧波損耗為計(jì)算得到的數(shù)值乘上系數(shù)kh,kh為電流I1Ih的二次方,h為諧波次數(shù)。
4.2.1 拉板不開(kāi)槽
表4為拉板不開(kāi)槽時(shí)計(jì)算得到的各個(gè)頻率下的損耗數(shù)值Ph,該數(shù)值是利用仿真結(jié)束后COMSOL自帶的后處理器計(jì)算得到的。具體過(guò)程為:對(duì)拉板上每一個(gè)節(jié)點(diǎn)的體損耗密度在一個(gè)周期內(nèi)取平均值,然后對(duì)其在整個(gè)拉板上進(jìn)行體積分。表中的頻率指數(shù)Ch計(jì)算式則為
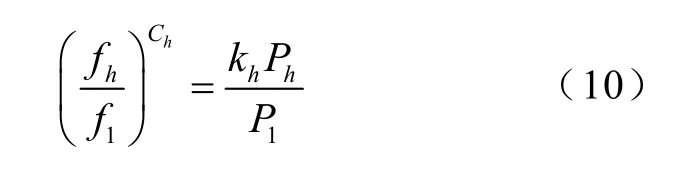
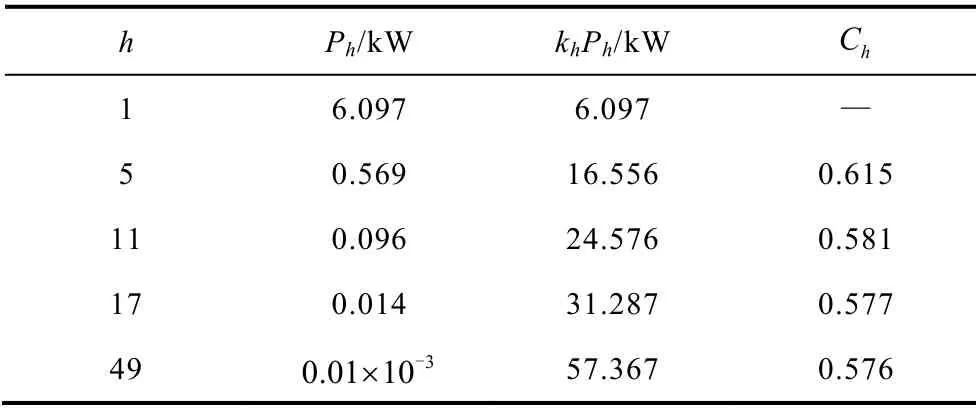
表4 換流變壓器拉板不開(kāi)槽渦流損耗Tab.4 Eddy current loss of flitch plate on converter transformer
從表4中可以看出當(dāng)拉板不開(kāi)槽時(shí),對(duì)于實(shí)際的換流變壓器負(fù)載電流頻譜而言,高次諧波損耗與基波損耗相比很小,17次諧波損耗僅為基波損耗的0.23%,49次諧波損耗則更小,幾乎可以忽略。而其頻率指數(shù)隨著電流頻率的增加逐漸減小,但變化的范圍很小,基本上在0.58上下浮動(dòng)。這與第2小節(jié)的理論推導(dǎo)結(jié)果0.5基本一致,兩者之間的誤差是由于沒(méi)有考慮拉板表面z軸方向磁場(chǎng)強(qiáng)度造成的少量渦流損耗導(dǎo)致的。綜上所述,當(dāng)換流變壓器拉板由于某些特殊需要選擇不開(kāi)槽時(shí),使用式(8)計(jì)算換流變壓器負(fù)載情況下的拉板損耗時(shí),其總損耗頻率指數(shù)可靠近低次諧波頻率指數(shù)取值,本文中的換流變壓器取值為0.6。
4.2.2 拉板開(kāi)兩全槽
表5為拉板開(kāi)兩全槽時(shí)計(jì)算得到的各個(gè)頻率下的損耗數(shù)值Ph和對(duì)應(yīng)的頻率指數(shù)Ch。與表4對(duì)比可以發(fā)現(xiàn),換流變壓器拉板開(kāi)槽之后,50Hz基波電流造成的渦流損耗大幅減小,約為不開(kāi)槽時(shí)的20%,減小了4/5。但是隨著電流頻率的增大,兩者之間的損耗差值逐漸減小,當(dāng)諧波次數(shù)大于5時(shí),對(duì)應(yīng)頻率下的拉板損耗則會(huì)大于不開(kāi)槽時(shí)的數(shù)值,且之后隨著頻率的增加,兩者之間的損耗差值逐漸增大。對(duì)于17次諧波損耗而言,其為基波損耗的1.85%,而不開(kāi)槽時(shí)僅為0.23%。當(dāng)諧波次數(shù)達(dá)到規(guī)定范圍內(nèi)的最大值49次時(shí),其造成的拉板損耗為不開(kāi)槽時(shí)的3.4倍,這與第2節(jié)理論部分給出的造成的損耗為不開(kāi)槽時(shí)3倍的結(jié)論基本吻合。上述結(jié)果的分析驗(yàn)證了理論推導(dǎo)的正確性:換流變壓器拉板開(kāi)槽會(huì)導(dǎo)致基波損耗的減小,但同時(shí)也會(huì)增加高次諧波損耗。所以拉板采用不銹鋼材料的換流變壓器,其開(kāi)槽數(shù)并不是越多越好,實(shí)際中開(kāi)2~3槽較為合適。而對(duì)于特殊情況下拉板采用磁鋼材料的換流變壓器,由于材料趨膚深度的大幅減小,拉板開(kāi)槽對(duì)拉板損耗的影響很小。
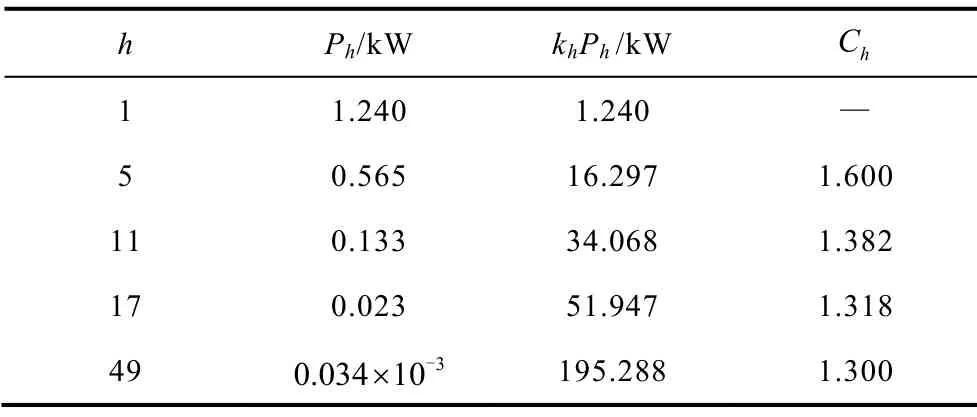
表5 換流變壓器拉板渦流損耗Tab.5 Eddy current loss of flitch plate on converter transformer
由于拉板開(kāi)槽導(dǎo)致諧波損耗占基波損耗的比重激增,因此其對(duì)應(yīng)的頻率指數(shù)也會(huì)大幅增大。電流頻率為250Hz時(shí),其頻率指數(shù)為1.6,是不開(kāi)槽時(shí)的2.46倍,之后隨著電流頻率的增加逐漸減小。雖然開(kāi)槽使得高次諧波的比重增加了,但其數(shù)值與總的損耗相比依舊很小,因此使用式(8)計(jì)算換流變壓器負(fù)載情況下拉板總損耗時(shí),其總的頻率指數(shù)仍然可以選取的靠近低次諧波,本文中可取數(shù)值1.5。該數(shù)值也與文獻(xiàn)[12]中實(shí)驗(yàn)得到的數(shù)值一致。由此可見(jiàn),若不考慮拉板開(kāi)槽的影響,依舊使用不開(kāi)槽時(shí)的指數(shù)0.6,將會(huì)對(duì)拉板總損耗的計(jì)算造成較大的誤差。
5 結(jié)論
本文通過(guò)對(duì)換流變壓器拉板表面磁場(chǎng)分布進(jìn)行簡(jiǎn)化,推導(dǎo)得到了拉板損耗的近似表達(dá)式,結(jié)合有限元仿真計(jì)算,研究了不同拉板開(kāi)槽情況下,電流頻率對(duì)拉板渦流損耗數(shù)值和損耗頻率指數(shù)的影響。主要結(jié)論如下:
1)換流變壓器拉板開(kāi)槽雖然會(huì)使基波損耗大幅減小,但同時(shí)也會(huì)增加高次諧波損耗,因此拉板采用不銹鋼材料的換流變壓器,其開(kāi)槽數(shù)并不是越多越好,實(shí)際中開(kāi)2或3槽較為合適。而對(duì)于特殊情況下拉板采用磁鋼材料的換流變壓器,拉板開(kāi)槽對(duì)拉板損耗的影響則很小。
2)換流變壓器拉板損耗的頻率指數(shù)受拉板開(kāi)槽數(shù)量和電流頻率影響:拉板開(kāi)槽數(shù)量越多頻率指數(shù)越大;電流頻率越大頻率指數(shù)越小。對(duì)于800kV特高壓換流變壓器,拉板采用不銹鋼材料的情況下,拉板損耗計(jì)算中不開(kāi)槽時(shí)頻率指數(shù)可取0.6,開(kāi)兩槽時(shí)可取1.5。

