應用于功率變換器的多繞組高頻變壓器模型

王迎迎 程 紅

（中國礦業大學（北京）機電與信息工程學院 北京 100083）

0 引言

功率變換器中的變壓器工作在多種勵磁狀態下，其等效電路模型以及非線性電感、漏感和電容參數影響了功率變換器的仿真精度。尤其在高頻電力電子變換器中，變壓器往往包含多個繞組，其繞制方法也復雜多樣，確定多繞組高頻變壓器的等效電路模型及參數有一定困難。多年來國內外學者對變壓器的精確建模進行了研究。T.Vu基于測量數據分析繞組的非線性特性和建模方法[1]。O.Mohammed通過對雙繞組變壓器實施電路——有限元的耦合分析提出了變壓器模型[2]。Xianming,Deng和C.Park利用有限元方法（Finite Element Method,FEM）研究變壓器的等效電路參數，并表明FEM適合分析幾何特性復雜的變壓器的非線性參數[3-4]。F.Starr和A.Boyajian研究了多繞組變壓器等效電路的建模，他們的等效模型被稱為星形等效電路[5-6]。星形電路中的元件參數可由端口測試結果確定。星形多繞組變壓器模型通常含有負電感，負電感并沒有物理意義。在過去的三十年中，負電感也一直被認為是引起數值振蕩的原因[7]。事實上，數值振蕩問題本質上是由于變壓器的勵磁支路并未正確連接導致的[8]。

在研究電磁瞬態問題時，BCTRAN是最常用的多繞組變壓器，電力系統仿真軟件EMTP中包含該模型[9]。該模型在確定參數時是基于端口測量結果計算漏磁阻抗的逆矩陣，從而避免矩陣求逆可能導致的病態矩陣問題。該模型在高頻下具有良好的數值穩定性，但BCTRAN變壓器模型的缺點在于沒有精確考慮變壓器的幾何形狀，且將表征磁心損耗的電阻只是簡單地并聯到最靠近磁心的繞組的勵磁支路上[10]。

對偶模型源于電路和磁路之間的對偶關系，其本質是將回路磁通方程轉換為節點電壓方程，亦即實現了磁路到電路的轉換[11-12]。對偶模型的拓撲較復雜，電路參數數量多，很難根據端口測量結果確定電路參數值，特別是對于包含大量磁化電感分支的多繞組變壓器。因此，本文考慮利用數值方法確定電路參數。

無論是端口模型（可以通過端口測量結果反推其參數的模型，例如星形電路和BCTRAN），還是對偶模型，研究人員面臨的最大的困難是如何準確地確定等效電路的參數。F.de León提出了一種新的用于低頻電磁瞬態分析的多繞組變壓器對偶模型[7]。在確定模型的漏感參數時，F.de León的做法是在傳統的對偶模型中增加互感和漏感，以此實現利用端口測量的信息確定對偶等效電路模型中的漏感參數。由于傳統的對偶模型中的漏感參數無法與多繞組變壓器短路測量得到的漏感參數個數相匹配，因此F.de León提出的基于短路測量結果計算互漏感的方法可以解決此問題。然而，對于繞組采用三明治繞法且跨層的多繞組變壓器，F.de León的參數確定方法不容易實現。

對于電路模型中的磁化電感，可以利用端口測量信息反推，也可利用解析公式計算，不過兩種方法在磁心非線性程度明顯時的計算誤差會增加[13]，尤其在磁心上開有氣隙時精度較差。多繞組變壓器對偶模型的拓撲復雜、參數多，端口測量信息及解析計算方法都不能確定模型的參數，因此本文提出利用有限元方法確定電路參數。為計算磁化電感，可在一次繞組端口施加多幅值的電流激勵，分析不同電流激勵下變壓器內部的磁場分布，確定變壓器磁路中的磁阻與通過的磁通的關系，磁阻的計算方法將在第3節中描述。根據計算的磁阻得到非線性磁化電感。為計算漏感，在所有繞組上施加低幅值激勵電流，然后基于磁場能量計算漏感參數，基于電場的數值仿真計算寄生電容參數。

利用本文提出的模型和參數確定方法建立用于反激變換器中的四繞組變壓器對偶模型，并將對偶電路仿真結果與多邊形模型仿真結果進行比較[14]。將提出的等效電路模型應用于反激變換電路中并進行電路仿真，將電路仿真結果與實驗結果進行比較以驗證模型的準確性。

1 對偶模型的建立

基于對偶原理建立的電路模型中的電路元件與變壓器繞組和磁心有對應的物理關系[12]。在建立對偶模型時，首先需要描繪變壓器的集總磁路模型，用集總磁路中的各部分磁阻來表征磁心、繞組和空氣中流過的磁通。基于描繪的集總磁路，通過方程轉換或者繪圖法便可得到電路模型。因此，電路模型中的參數與物理結構一一對應。

本文以反激變換器中的四繞組變壓器為例，闡述等效電路模型的建立方法。四繞組變壓器的結構如圖1所示，變壓器選用平面磁心，以實現緊湊結構設計和工藝穩定性。一次繞組用P48表示，分為四層，采用串聯連接；二次繞組用S15、S5和Vcc15表示，分別由兩層線圈串聯連接。表1給出了四繞組變壓器的參數。磁心選用牌號為PC90的鐵氧體材料，當頻率小于1MHz且溫度在40～280℃范圍時，該材料具有相對穩定的磁導率和較低的損耗。用于反激變換器拓撲結構的變壓器應具有存儲能量的能力，為避免磁心飽和，布置0.5mm的氣隙。繞組印制在印制電路板（Printed Circuit Board,PCB）中，以提高變換器的功率密度。

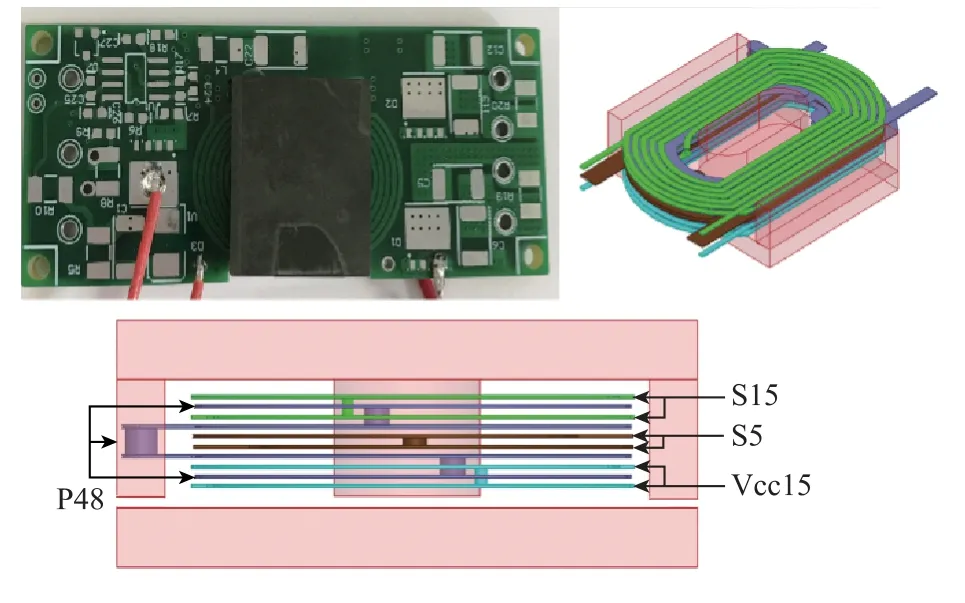
圖1 四繞組反激變壓器模型與結構Fig.1 Prototype and model of a four-winding fly-back transformer

表1 四繞組變壓器參數Tab.1 Specifications of the four-winding transformer

多繞組變壓器的磁路拓撲如圖2所示。其中，流經磁心柱的磁通路徑用Rm表示，流經鐵軛的磁通路徑用Rmu和Rmd表示；流經氣隙的磁通路徑由Rmair表示；漏磁通路徑由R1～R8表示。由于中間兩層繞組是串聯連接，可忽略它們之間的漏磁通。由磁路轉換為電路時，在每個磁阻上設置電感，并在磁路的每個網格中設置節點[12]，進而得到如圖3所示的對偶電路模型。其中，磁化電感用Lm表示，漏感用L表示。將繞組之間的寄生電容加到相應的繞組間。

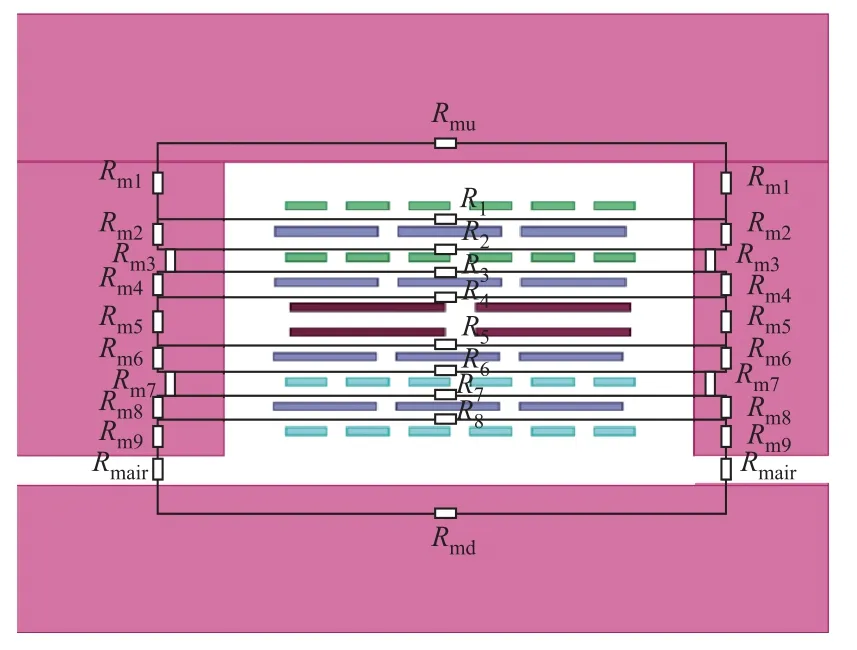
圖2 多繞組變壓器磁路拓撲Fig.2 Reluctance circuit for the multi-winding transformer

2 模型參數確定

得到圖3所示的電路模型后，需要確定模型參數，包括磁化電感、漏感、電容參數。磁心損耗不是本文研究的重點，故在圖3中并未給出表征磁心損耗的電阻。對于考慮磁心損耗的情況，將表征磁心損耗的電阻與各磁化電感并聯即可。考慮利用有限元數值方法分析平面變壓器的磁場和電場，基于磁場的分布確定圖3中所示的磁化電感和漏感，基于電場分布確定分布電容參數。

圖3 基于對偶關系的電路模型Fig.3 Equivalent electric circuit based on the principle of duality

2.1 磁化電感參數的確定

由于端口的測量信息不足以確定多個磁化電感，因此考慮先確定各個磁阻值，再轉換得到電感值。在確定磁阻參數時，可利用有限元數值計算的磁場分布結果計算磁阻。

建立三維變壓器模型，設置磁心材料時選擇溫度為100°C時的單極磁化曲線。在初級繞組端口施加電流激勵。得到的磁場能量密度如圖4所示，磁感應強度如圖5所示。圖4中，變壓器磁心被分成多個部分，同時各部分磁阻的磁通積分面如圖5所示。利用各部分磁阻內部的磁場能量W和流過磁阻的磁通Φ計算磁阻值為

圖4 四繞組變壓器內部的磁場能量密度Fig.4 Magnetic energy density of the four-winding transformer

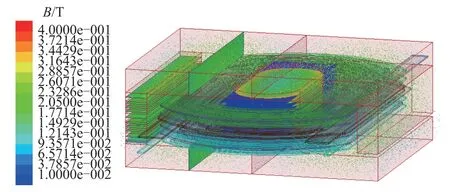
圖5 磁感應強度的分布Fig.5 Distribution of the magnetic flux density

在式（1）中，通過對磁心各部分的能量進行積分計算磁場能量W，通過對磁心各部分中間橫截面的磁感應強度進行積分近似計算流經磁阻的磁通Φ。

表2所示為激勵電流等于4A時磁心各部分磁阻Rmi的磁場能量Wmi。表3所示為在此激勵下流經各部分磁阻的磁通Φmi。此激勵下各個磁阻的Rmi值見表4。相應的磁化電感Lmi計算式為

表2 各部分磁阻的能量Tab.2 Energy of each section

表3 積分截面的磁通Tab.3 Flux of the integral surface

表4 多繞組變壓器的磁阻Tab.4 Reluctance of the multi-winding transformer

式中，N為已轉換為一次繞組的匝數，計算的磁化電感見表5。

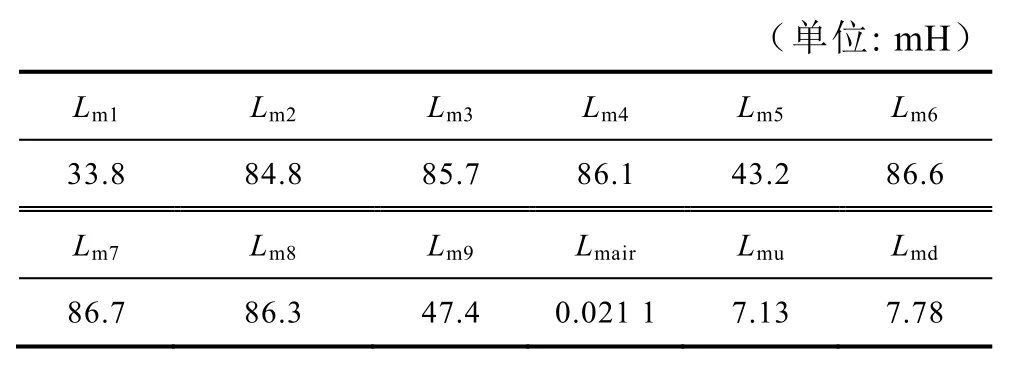
表5 額定電流下變壓器的電感Tab.5 Magnetizing inductance of the multi-winding transformer when applying rated current

由于磁心的非線性特性，當勵磁電流變化時，磁阻的值隨磁通量變化。因此，假如端口施加不同的激勵電流，就可得到磁阻和磁通之間的非線性關系。非線性磁阻可以用以磁通為自變量的函數來表示，然后，經過轉換可得到以電流為自變量的非線性磁化電感。圖6給出了幾個典型的非線性電感。非線性電感可由Φ和i之間的關系表示。本質上，本文在確定變壓器等效電路參數的非線性曲線時，使用的是“打點法”，即每施加一個幅值一定的直流電流進行靜態場分析，可得到“非線性曲線上的一個點”。通過分析多個幅值下的磁場獲得多個點，進而描述非線性曲線。靜態場的單點分析可保證較高的精度。

圖6 典型電感的非線性曲線Fig.6 Nonlinear curves for several typical inductances

本文提出的確定參數的方法沒有在激勵方式中體現頻率對模型參數的影響，但在數值仿真的材料設置時體現了頻率的影響。頻率對參數的影響體現在對磁心和導線的影響。磁心的磁化曲線和損耗曲線都隨著頻率變化，本文在用數值仿真確定參數時，設置的磁心材料曲線為表6所示的非線性曲線（頻率為100kHz），以提高參數在高頻時的準確性。

表6 磁心磁化曲線的典型數據Tab.6 Typical data of magnetization curve of the core

2.2 漏感參數的確定

對于傳統的變壓器，漏感通常通過變壓器端口的短路測試獲得。對于含有N個繞組的變壓器，存在N(N-1)/2對不同的短路情況。對于四繞組變壓器，通過短路測試可獲得六個漏電感，見表7。然而，繞組之間的這六個漏電感不能直接與圖3中所示的八個漏感匹配。為了解決這個問題，可使用耦合電感將測得的漏電感與對偶模型中的漏電感匹配[7]。然而，漏感的這種表示方法并不適用于包含跨層繞組結構的變壓器。

表7 短路測量的繞組間漏感Tab.7 Leakage inductances between windings obtained by short-circuit tests

本文考慮利用數值計算確定變壓器模型的漏感參數。在一次繞組和二次繞組同時施加激勵電流，保持一次繞組和二次繞組的磁通勢相同。設置一次繞組的勵磁電流為3A，二次繞組S15、S5和Vcc的勵磁電流分別為1A、3A和1A。變壓器中的漏磁能量分布如圖7所示，同時漏磁能量值Wi在表8中給出。由于層間絕緣介質的磁阻遠大于鐵氧體磁心，因此可認為磁通勢全部集中在絕緣介質的磁阻上。基于漏磁能量和磁通勢，可以得到層間的漏電感。將層間漏感Li轉換到一次側，其值見表9。

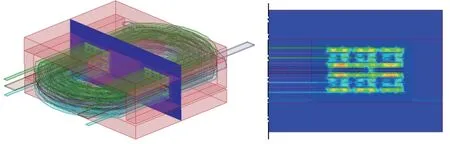
圖7 漏磁能量分布Fig.7 Distribution of the leakage energy

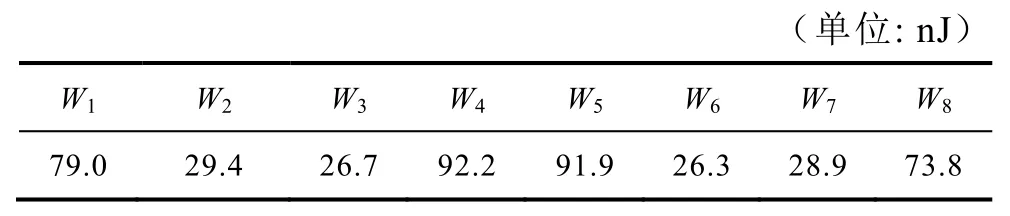
表8 漏磁部分的能量Tab.8 Energy of each leakage region

表9 層間漏感Tab.9 Leakage inductance between layers

得到磁化電感和層間漏感后，可對圖3所示的等效電路進行電路仿真。對幾個繞組的端口分別設置短路，利用電路仿真可以模擬端口試驗，據此可以得出繞組之間的漏電感。例如，如果對一次繞組P施加電壓激勵并使繞組S15短路，同時保持繞組S5和繞組Vcc斷開，則可以獲得繞組P和繞組S15之間的漏電感。變壓器中有四個繞組，最終可在繞組之間獲得6個漏電感，見表10中第三行所示。將變壓器端子上的短路測試結果列于表10第二行。比較發現，模擬和測試的結果之間的差異低于7%。通過這種方式，也驗證了數值計算確定的漏感值的準確性。

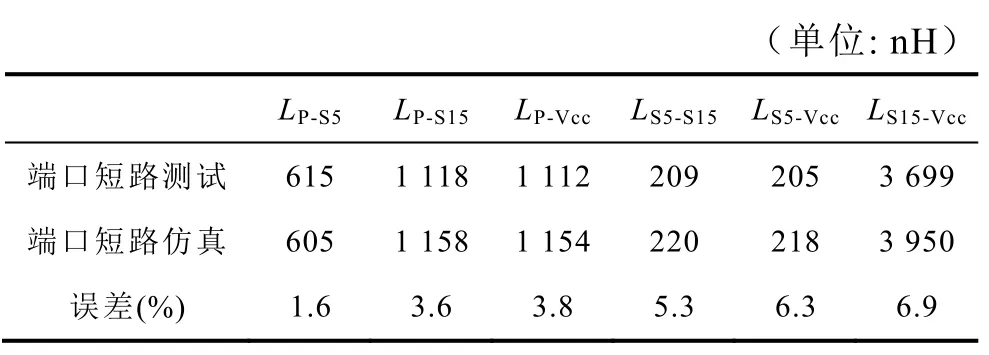
表10 四繞組之間的漏感Tab.10 Leakage inductances between 4 windings

2.3 分布電容參數的確定

多繞組變壓器的分布電容包括接地磁心和繞組之間的電容、繞組之間的電容及同一繞組各層之間的電容。確定電容參數時可用能量法，即根據變壓器中的電場能量計算寄生電容參數。利用三維有限元法仿真分析變壓器內部的電場，電場能量分布的情況如圖8所示，進而確定四繞組之間分布電容參數，見表11。

圖8 四繞組變壓器內部的電場能量密度Fig.8 Electric energy density of the four-winding transformer

表11 繞組間電容Tab.11 Capacitances between windings

3 模型的驗證

3.1 對偶電路仿真與場路耦合仿真的比較

由于在場路耦合分析時，變壓器的瞬態場數值計算中不能考慮內部的寄生電容，所以為了保持一致性，在利用場路耦合的分析結果驗證電路模型時，電路仿真并未考慮圖3中的各個電容分支。利用場路耦合分析的結果僅可驗證對偶等效電路中電感參數的準確性。

仿真時，變壓器的一次側由脈沖電壓源（100kHz,15V）供電。圖9所示為場路耦合和對偶模型得到的輸出波形，匹配良好的前沿波形說明了等效電路中勵磁電感和漏電感具有較好的精度。

圖9 場路耦合模型和對偶模型仿真得到的輸出波形Fig.9 Output waveforms obtained by the field-circuit coupled analysis and the duality model simulations

3.2 對偶電路仿真與多邊形模型仿真的比較

圖10中所示為四繞組變壓器的多邊形模型，利用端口的測試結果可確定多邊形模型中的電感值，電容值可直接采用有限元分析得到的分布電容值[15-17]。如圖10中所示，多邊形模型的電感參數存在負值，這是由端口結果反推產生的，沒有物理意義，負電感在一些情況下會導致復雜電路仿真發生振蕩。

圖10 四繞組變壓器的多邊形模型Fig.10 Polygon model for the four-winding transformer

在變壓器的一次側設置脈沖電壓源（100kHz，15V），比較包含電容的對偶模型的電路仿真結果與多邊形模型的仿真結果。圖11所示為兩種模型的輸出波形，波形的過沖匹配良好。由于漏感和寄生電容是影響過沖的關鍵參數[18-19]，因此匹配良好的過沖波形驗證了等效電路中的漏感和電容參數的精度。

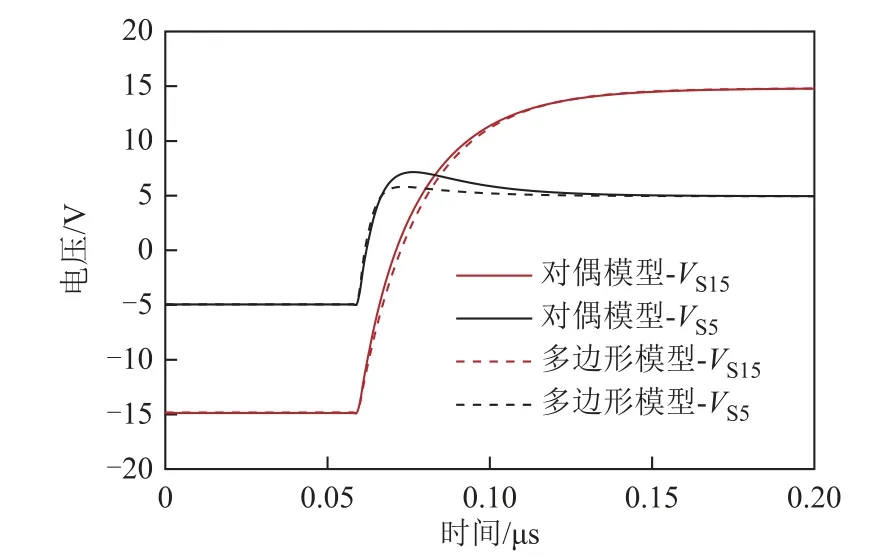
圖11 多邊形和對偶模型仿真得到的輸出波形Fig.11 Output waveforms obtained by the polygon model and the duality model simulations

3.3 對偶模型在反激變換器中的應用

本文搭建了一個反激變換器以驗證對偶模型的適用性。反激變換器的電路拓撲如圖12所示。激勵源是輸出為48V的直流電源。剩余電流裝置（Residual Current Device,RCD）吸收電路中的電容為1nF，吸收電阻為500?。變換器設置在非連續導通模式（Discontinuous Conduotion Mode,DCM）下工作，占空比設置為0.26。三個二次繞組的負載設置分別為RS5=10?，RS15=19?，RVcc=19?。圖13給出部分試驗結果，包括MOSFET的漏極和源極之間的電壓Vds和一次電流iP。圖14是等效電路拓撲的仿真結果，其與測量結果的一致性好。

圖12 驗證對偶模型的反激變換電路Fig.12 Circuit prototype of a fly-back converter for verification of the duality model

圖13 DCM狀態下測量的電壓VdsFig.13 Measured voltage Vds under DCM

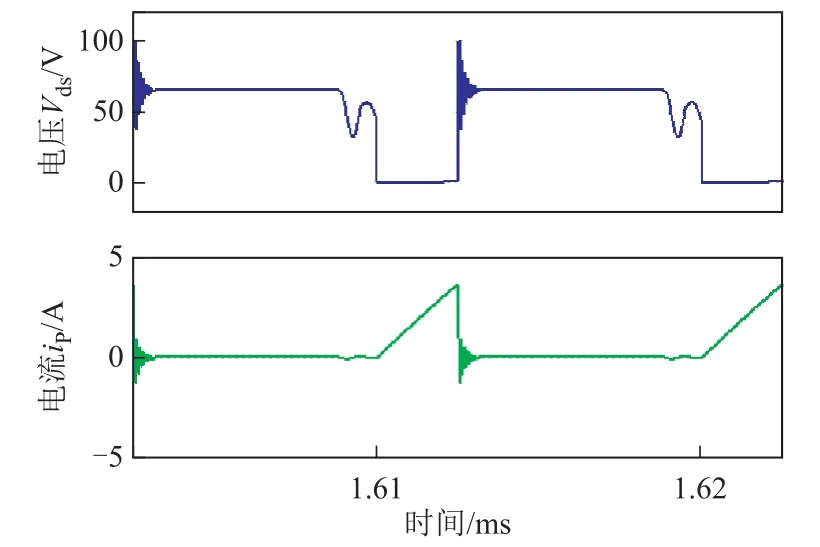
圖14 DCM狀態下電路仿真得到的電壓VdsFig.14 Simulated voltage Vds under DCM

當MOSFET關斷時，流過漏感的電流不會突然改變，電流的變化將產生感應電動勢。如測量和仿真結果所示，當MOSFET關斷時，由于感應電動勢和二次反射電壓，Vds遠大于48V的輸入電壓。存儲在漏感中的能量將通過RCD吸收電路釋放[20]。圖15比較了MOSFET關斷時Vds前沿波形的過沖和振蕩。關斷MOSFET時，Vds的過沖和振蕩與漏感和寄生電容參數密切相關。因此，比較測量和仿真得到的Vds的過沖波形，可以驗證對偶變壓器等效電路的有效性。觀察到測量和模擬結果在幅度和振蕩周期中匹配得較好，電路仿真波形振蕩時間比測量波形略短，其振蕩的階數比測量結果略低。提出的高階等效電路模型及參數確定方法在分析高頻問題時可保證較好的準確性。

圖15 測量結果和仿真結果的比較Fig.15 Comparison of measured and simulated waveforms

此外，在MOSFET導通之前，二次電流已降至零，Vds大于輸入電壓。它使MOSFET的結電容和磁化電感產生共振。從圖13和圖14中可以看出，在MOSFET導通之前Vds波形在衰減系數和頻率方面略有不同。這是因為未能精確地估計MOSFET的漏極-源極電容和引線電感。

4 結論

本文提出了應用于功率變換器中的多繞組且含跨層繞組結構時高頻變壓器的等效電路模型，并提出了利用有限元場分布結果確定非線性電感、漏感及電容參數的方法。提出的方法很好地解決了跨層繞組的參數確定問題。通過與多邊形模型仿真及試驗分析結果的比較驗證了多繞組高頻變壓器等效電路的準確性。本文為對偶模型在多繞組高頻變壓器的應用提供了方法基礎。