基于Logistic映射的蜉蝣優化算法

陳嘉豪 童楠 符強

摘要： 在高維復雜問題上，蜉蝣優化算法存在易陷入局部最優區域且求解精度較差等問題，因而提出基于Logistic映射的蜉蝣優化算法。引入依據Logistic映射的混沌機制，當種群進化停滯時，當前最優蜉蝣通過混沌機制尋找適應度更好的蜉蝣，以激發種群進化能力;建立較劣蜉蝣加速進化機制，激勵蜉蝣個體以達到種群尋優要求;采用動態慣性權重均衡算法全局和局部的搜索性能。抽取5個benchmark函數測試算法性能，實驗結果驗證了所提算法在尋優性能上的有效性。

關鍵詞： 群智能算法; 蜉蝣優化算法; Logistic映射; 擾動; 動態慣性權重

中圖分類號：TP301.6? ? ? ? ? 文獻標識碼：A? ? ?文章編號：1006-8228（2021）10-06-05

Mayfly optimization algorithm based on Logistic mapping

Chen Jiahao， Tong Nan， Fu Qiang

（College of Science and Technology， Ningbo University， Ningbo， Zhejiang 315300， China）

Abstract： For high-dimensional complex problems， mayfly optimization algorithm has problems such as easy to fall into local optimal area and poor solution accuracy. Therefore， a mayfly optimization algorithm based on Logistic mapping is proposed. Introducing the Logistic mapping based chaotic mechanism， when the evolution of the population stagnates， the current optimal mayfly uses the chaotic mechanism to find a mayfly with better adaptability to stimulate the evolutionary ability of the population; Establishing a accelerated evolution mechanism for inferior mayfly， the mayfly individual is motivated to meet the requirements of the population optimization; Using the dynamic inertial weight balance algorithm， the global and local search capabilities are balanced. Five benchmark functions are selected to test the performance of the algorithm， and the experimental results verify the effectiveness of the proposed algorithm in optimizing performance.

Key words： swarm intelligence algorithm; mayfly optimization algorithm; Logistic mapping; disturbance; dynamic inertia weight

0 引言

群智能優化算法[1-2]易于編程，尋優能力強，現已廣泛應用于實際工程領域中，例如解決旅行商問題和0-1背包問題等[3-4]。

蜉蝣優化算法[5]（A mayfly optimization algorithmMA）是一種2020年7月由Konstantinos Zervoudakis和 Stelios Tsafarakis 提出的新型群智能算法，此算法受蜉蝣飛行行為和交配過程的啟發，聯結粒子群算法[6]和遺傳算法[7]的優點，在低維問題上，相比較其余群智能算法具備更好的收斂速度和收斂精度，且算法中的隨機飛行和婚禮舞蹈行為能有效平衡種群的全局探索及局部搜索要求。但當遇到高維復雜問題時，蜉蝣算法單純依靠自身機制仍然較難跳出局部最優區域，且由于蜉蝣在移動時步長太短，導致算法收斂精度不高。

針對上述問題，本文提出基于Logistic映射的蜉蝣優化算法（mayfly optimization algorithm based on Logistic mapping LMA），采用動態慣性權重提高種群的搜索能力，增加算法收斂效率;引入基于Logistic映射的混沌機制，防止種群出現早熟收斂現象;建立較劣蜉蝣加速進化機制，減少較劣蜉蝣在外徘徊的次數，提升種群整體進化速度。通過對標準測試函數的仿真實驗，并與其他幾種算法進行比較，驗證LMA算法對問題求解的有效性。

1 蜉蝣優化算法簡介

蜉蝣優化算法抽象出蜉蝣的生命過程，將蜉蝣的位置映射為問題的潛在解決方案。算法最初隨機生成蜉蝣種群，將種群分為雄性蜉蝣群和雌性蜉蝣群。設一個[D]維問題，第[i]個蜉蝣的位置為[xi={x1，x2，x3，…，xD}][xi={x1，x2，x3，…，xD}][xi={x1，x2，x3，…，xD}]，對應速度為[Vi={V1，V2，V3，…，VD}]。

1.1 雄雌蜉蝣的移動

MA算法中雄蜉蝣會朝更優方向進化，因此雄蜉蝣的速度將根據自身曾到過的最好位置與種群當前最優位置來調整，且當蜉蝣適應度優于種群當前最優適應度時，蜉蝣將根據婚禮舞蹈系數和慣性權重對速度進行調整，速度更新公式為：

[vt+1ij=g*vtij+a1e-βr2ppbij-xtij+a2e-βr2ggbj-xtij，iffxi>fgbg*vtij+d*r1 ，iffgb≤fxi] ⑴

其中[vtij]為第[t]次迭代第[i]個蜉蝣在[j]維度上的速度，[xtij]為第[t]次迭代時第[i]個雄蜉蝣在[j]維度上的位置，[a1]為蜉蝣個體的認知參數，[a2]為種群社會貢獻參數，[g]為慣性權重，[β]是一個固定的能見度因子，[d]為舞蹈因子，[r1]是[[-1，1]]內的隨機因子，[pbij]為第[i]個蜉蝣在第[j]維曾經到達過的最好的位置，[gbj]為第[j]維全局最好的位置，[rp]與[rg]分別為第[i]個蜉蝣與[pb]的笛卡爾距離和第[i]個蜉蝣與[gb]的笛卡爾距離。

個體適應度排序等級相同的雄雌蜉蝣將會相互吸引，雌蜉蝣的移動依據為排序等級相同的雄蜉蝣位置。若雄蜉蝣優于雌蜉蝣，則雌蜉蝣向雄蜉蝣靠近，否則受隨機飛行因子的影響隨機向周圍飛行。雌性蜉蝣的速度更新公式為：

[vt+1ij=g*vtij+a2e-βr2mfxtij-ytij ，iffyi>fxig*vtij+fl*r1? ?，iffyi≤fxi] ⑵

其中[ytij]為第[t]次迭代時第[i]個雌蜉蝣在[j]維度上的位置，[rmf]為雄雌蜉蝣之間的笛卡爾距離，[fl]是一個隨機飛行因子。

MA算法通過在當前位置上添加速度[vt+1i]作為雄雌蜉蝣位置的移動。

[xt+1i=xti+vt+1i] ⑶

同時為防止蜉蝣速度無限增大導致蜉蝣飛出解空間范圍，MA算法對蜉蝣的速度進行限定。在迭代的過程中，為滿足算法后期局部探索要求，蜉蝣的慣性權重、婚禮舞蹈因子與隨機飛行因子將逐漸減少。

1.2 雄雌蜉蝣的交配與變異

MA算法中個體適應度排序等級相同的雄雌蜉蝣將會相互交配生成子代蜉蝣。交配的公式如下：

[offspring1=L*male+1-L*female]

[offspring2=L*female+1-L*male]? ⑷

其中[offspring]為子代蜉蝣，[male]為雄蜉蝣，[female]為雌蜉蝣，[L]為[[-1，1]]中的隨機因子。

MA算法引入高斯變異[8]，對子代蜉蝣的單個維度進行基因變異。子代蜉蝣的變異個數以種群數量[Pop]為基數，定義變異幾率為[mu]，[Pop*mu]為種群中子代的變異個數。變異公式如下：

[offspringn=offspringn+σ*Nn（0，1）]? ⑸

其中[Nn0，1]為平均值為0，方差為1的標準正態分布隨機數，[σ]為正態分布的標準差，[offspringn]為變異蜉蝣的第[n]個維度。

2 改進的蜉蝣優化算法

2.1 根據Logistic映射的混沌機制

基于Logistic映射的混沌機制[9]中存在控制參數[μ∈[0，4]]，當[μ]等于4時，混沌變量的取值將呈現混沌特征，因此本文取[μ]為4。該混沌機制將生成隨機分布在解空間中的混沌蜉蝣。LMA算法由當前最優蜉蝣隨機產生[10]個混沌蜉蝣，若最優的混沌蜉蝣優于當前最優蜉蝣，則替換之，否則隨機替換蜉蝣種群中除了最優蜉蝣外的任一蜉蝣，增加種群多樣性，增大算法求得全局最優解的可能性。

Logistic映射的混沌機制進行擾動的公式如下：

[zt+1i=μzti（1-zti）] ⑹

其中[zti∈[0，1]]為第[i]個混沌蜉蝣的混沌位置。

將[xi∈[xmin，xmax]]映射到[zi∈[0，1]]的公式如下：

[zi=（xi-xmin）/（xmax-xmin）] ⑺

將[zi]映射回[xi]公式為：

[xi=xmin+zi（xmax-xmin）] ⑻

當連續兩次迭代的種群蜉蝣的平均適應度之差小于[10-3]，判定算法陷入局部最優，將執行混沌機制。

方差[10]計算公式如下：

[σ2=i=1N（（fi-favg）/f）2] ⑼

其中N為種群中蜉蝣的總數，[favg]為種群適應度的平均值，[fi]為蜉蝣個體[i]的適應度。[f]為用來限制[σ2]大小的因子，計算公式為：

[f=maxfi-favg，maxfi-favg>11? ? ? ? ? ? ? ? ? ? ? ? ? ? ?，max {|fi-favg|}≤1] ⑽

2.2 較劣蜉蝣加速進化機制

種群中存在部分個體的進化程度始終無法達到種群平均進化程度，算法將判定這類個體為失效個體。對多次無法跟隨種群進化腳步的蜉蝣進行加速進化操作，激發失效蜉蝣的潛能以增加算法收斂速度。當蜉蝣無法跟隨種群進化腳步的次數超過3次時，實施加速操作[11]，蜉蝣與當前最優解的適應度差值與拉伸因子成正比，從而影響蜉蝣的速度。加入拉伸因子[SO]后的蜉蝣速度公式為：

[vtij=g*vtij+a1e-βr2ppbij-xtij][+a2e-βr2ggbj-xtij+SO] ⑾

其中[SO]為拉伸因子，其計算公式為：

[SO=c3*r2*（gbest-pbest）] ⑿

其中[c3]的計算公式為：

[c3=（xcost-gcost）/（avecost-gcost）] ⒀

其中[xcost]為蜉蝣的適應度，[gcost]為全局最優解的適應度，[avecost]為種群平均適應度。

2.3 動態慣性權重

為平衡算法全局搜索能力與局部探索性能，算法前期以較小的慣性權重減小蜉蝣步長，保持種群多樣性，中期增大慣性權重，加強全局搜索能力，后期減小慣性權重，增強局部探索性能，增加算法收斂精度，所以本文采用二次函數改變慣性權重，公式如下：

[g=-4gmax-gminMaxIt2*it2+][4gmax-gminMaxIt*it+gmin] ⒁

其中[gmax]為最大慣性因子;[gmin]為最小慣性因子，[MaxIt]為最大迭代次數，[it]為當前迭代次數。

2.4 LMA算法流程

Step1 初始化參數，初始化雄雌蜉蝣位置與速度，并計算適應度，尋找當前最佳適應度。

Step2 更新蜉蝣速度與位置，判斷蜉蝣無法跟隨進化的次數，若超過3次，則按式⑿更新速度，否則按式⑴和式⑵更新速度，并計算適應度。

Step3 根據式⑷生成后代數量為nm，根據變異可能性mu和式⑸產生變異后代，并將各個后代隨機插入雄蜉蝣或雌蜉蝣隊列。

Step4 根據種群的適應度實行精英保留策略。

Step5 按式⑼計算本次種群解的方差值，并與上一代種群的方差作比較，若差值小于[10-3]，則按式⑹～式⑻執行混沌機制。

Step6 更新舞蹈因子，隨機飛行因子，更新慣性因子。

Step7 迭代次數加一，判斷是否到達迭代上限，若是則轉Step8，若否則轉Step2。

Step8 輸出種群歷史最優解。

3 實驗及結果分析

3.1 測試函數

為驗證LMA的算法性能，隨機抽取5個benchmark標準測試函數。其中F1、F2為單峰函數，用來測試算法的全局尋優能力，F3、F4為高維多峰函數，用來檢測算法對復雜問題的處理能力。F5函數在最優點附近較為狹窄，用于測試算法的局部搜索能力。測試函數相關參數設置見表1。

3.2 算法參數設置

在解決高維問題時，群智能算法常常較難獲得很好的結果，為驗證LMA算法在處理高維問題上的尋優能力，設計在50維問題上的對比實驗。設置迭代次數為2000次，種群數量為40。實驗對比蜉蝣算法（MA），本文所提算法（LMA），經典蜂群算法（ABC）[12]和基于混沌序列的蜂群優化算法（CABC）[13]四種算法，LMA算法的參數設置可參照表2，其他算法參數設置參考文獻。

3.3 實驗數據及分析

實驗將每個算法對每個問題獨立測試100次記錄算法結果的平均值，最優解，最劣解和方差。

表3中記錄四種算法對每個測試函數進行測試后的數據。在F1、F2測試函數上，LMA算法對比其他算法的平均值、最優值、最劣值和方差都有較為明顯的優勢，說明LMA算法的尋優能力更強、魯棒性更好。對比MA算法與ABC算法，LMA算法與CABC算法都采用混沌機制，在處理F3、F4函數時，最優值上有較大的優勢，說明采用該機制使算法處理多峰復雜問題的能力有所提升。綜上所述，LMA算法的改進策略有效地提升算法對處理高維問題的能力，提高了算法尋優性能。

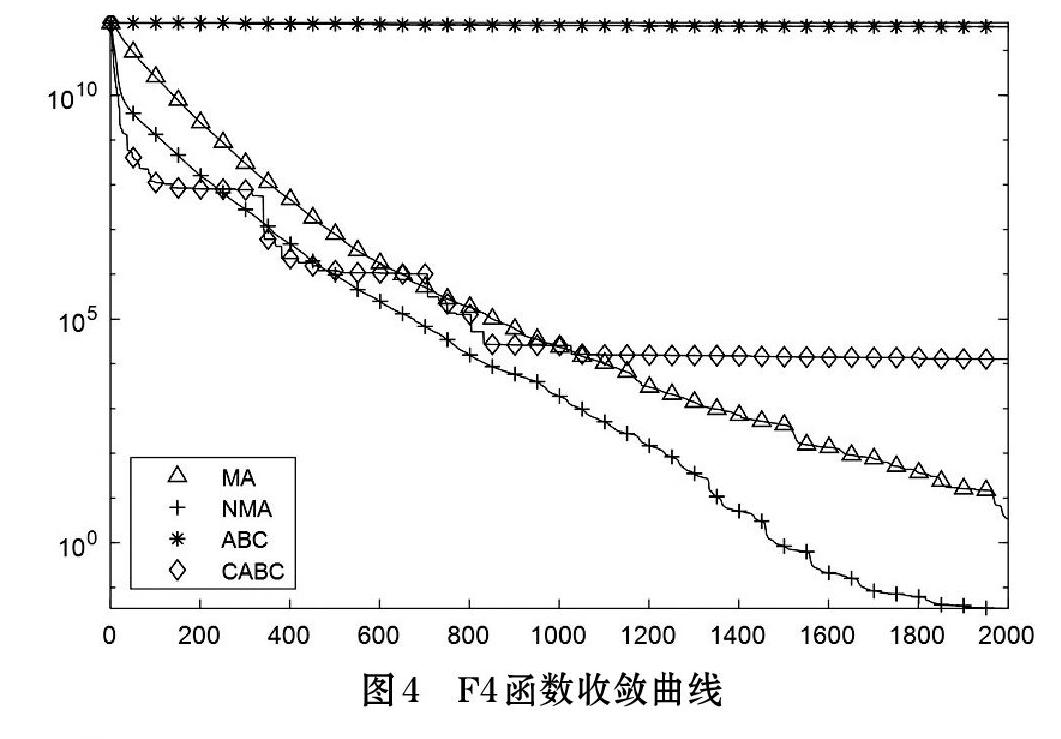
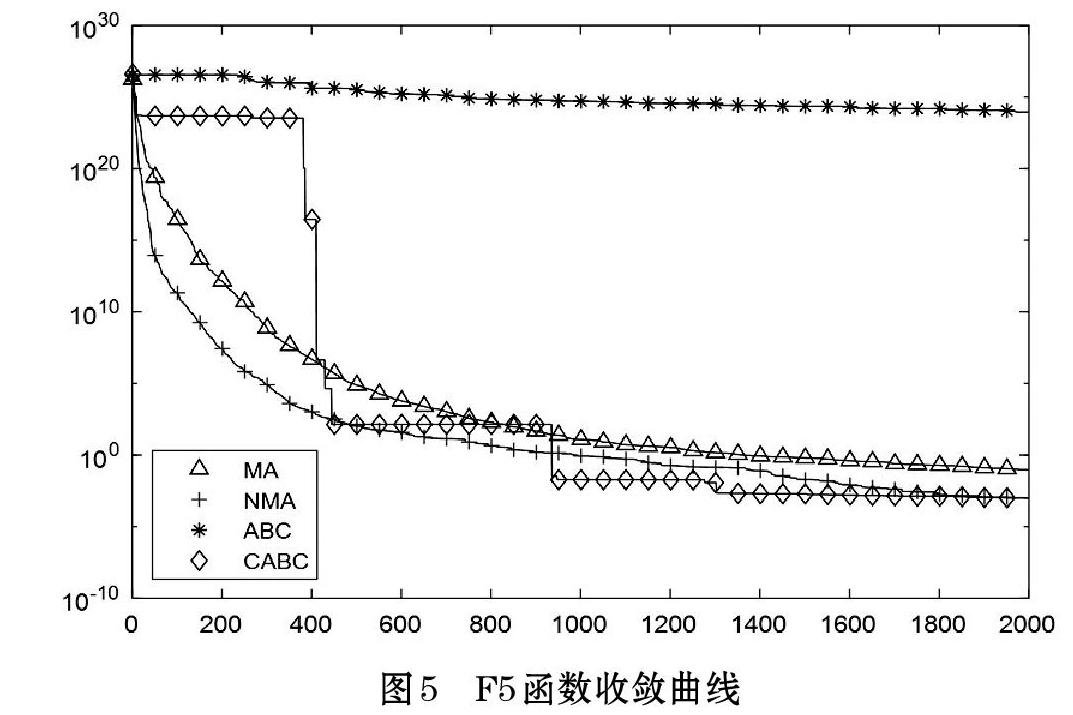
為更加直觀地體現LMA算法的優越性能，繪制出圖1～圖5仿真四種算法的收斂曲線。

在局部搜索能力方面，參照F5函數，觀察函數收斂曲線，ABC算法較難向下收斂，CABC算法依靠混沌策略可以向下尋優，但尋優過程不穩定，魯棒性較差。MA算法較為有效地向下尋優，但對比LMA算法的收斂曲線，LMA算法的求解精度更為準確，收斂效率更高。因此相比較其他算法，LMA算法在局部搜索能力上更強;在算法全局搜索能力方面，對比F2函數曲線可以看到LMA算法在算法中后期的收斂效率明顯優于其他三種算法;在改進策略的有效性方面，全面對比函數曲線，LMA算法在迭代前期收斂效率高于MA算法，在迭代后期，LMA算法對于部分容易陷入局部最優的函數仍然可以向下尋優，這說明改進策略有效地提升算法的尋優能力，增強算法對求解陷入困境的處理能力。

4 結束語

MA算法本身在收斂效率、全局搜索能力和局部搜索能力上，比一般群智能算法更好，本文針對MA算法在高維度復雜問題上易陷入局部最優區域和求解精度較低等問題，提出改進算法，實驗證明在種群進化停止時，LMA算法的處理能力比MA算法更好，在尋優能力方面，LMA算法也展現出更好的性能，下一步研究方向為加快算法的收斂速度。

參考文獻（References）：

[1] Guo X D， Zhang X L， Wang L F， et al. Fruit Fly

Optimization Algorithm Based on Single-Gene Mutation for High-Dimensional Unconstrained Optimization Problems[J].Mathematical Problems in Engineering，2020.

[2] 王習濤.一種優化局部搜索能力的灰狼算法[J].計算機時代，2020.342（12）：57-59

[3] 何錦福，符強，王豪東.求解TSP問題的改進模擬退火算法[J].計算機時代，2019.7：47-50

[4] 劉生建，楊艷，周永權.求解0-1背包問題的二進制獅群算法[J].計算機工程與科學，2019.41（11）：179-187

[5] Zervoudakis K， Tsafarakis S. A mayfly optimizationalgorithm[J].Computers & Industrial Engineering，2020.145：106559

[6] Liu Z， Qin Z， Zhu P， et al. An adaptive switchover hybrid particle swarm optimization algorithm with local search strategy for constrained optimization problems[J].Engineering Applications of Artificial Intelligence，2020.95：103771

[7] Hou L， Zou J， Du C， et al. A fault diagnosis model of? marine diesel engine cylinder based on modified genetic algorithm and multilayer perceptron[J]. Soft Computing，2020.24（2）.

[8] 李永恒，趙志剛.基于越界重置和高斯變異的蝙蝠優化算法[J].計算機工程與科學，2019.41（1）：144-152

[9] 韓雪娟，李國東，王思秀 基于Logistic和超混沌結合的加密算法[J].計算機科學，2019.46（0z2）：477-482

[10] 王亞，熊焰，龔旭東，陸琦瑋.基于混沌PSO算法優化RBF網絡入侵檢測模型[J].計算機工程與應用，2013.49（10）：84-87

[11] 李榮龍，羅杰.一種改進的粒子群優化算法[J].計算機技術與發展，2015.25（7）：67-71

[12] 何堯，劉建華，楊榮華.人工蜂群算法研究綜述[J]. 計算機應用研究，2018.319（5）：7-12

[13] 羅鈞，李研.具有混沌搜索策略的蜂群優化算法[J].控制與決策，2010.25（12）：1913-1916